8a5b571ed40e0462099cf9c253e8ec85.ppt
- Количество слайдов: 28

Review for Exam 2 n Subject matter: n n n Chapters from Bishop’s book: n n Covers topics not included in Exam 1 RBAC and Chinese Wall Policies Cryptography Network Security and Authentication 7, 9, 10, 11, 12 The nature of the exam: n n n 4 -5 questions Similar to the homework. Pseudo-code, algorithms, protocols, etc. 1
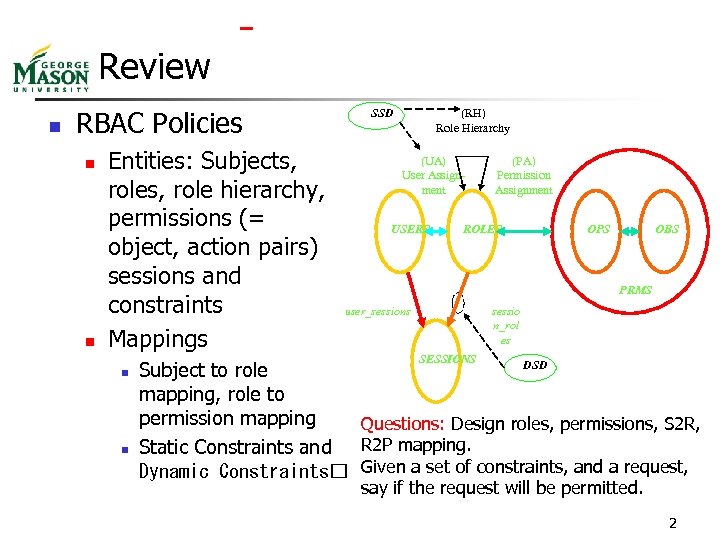
Review n RBAC Policies n n Entities: Subjects, role hierarchy, permissions (= object, action pairs) sessions and constraints Mappings n n (RH) Role Hierarchy SSD (UA) User Assignment USERS (PA) Permission Assignment ROLES OPS OBS PRMS user_sessions sessio n_rol es SESSIONS DSD Subject to role mapping, role to permission mapping Questions: Design roles, permissions, S 2 R, Static Constraints and R 2 P mapping. Dynamic Constraints Given a set of constraints, and a request, say if the request will be permitted. 2

Chinese Wall Policy (Chapter 7) n n n Conflict of Interest Classes History based access control Prevents information leakage from one competitor to another CW-simple security property CW-* property 3
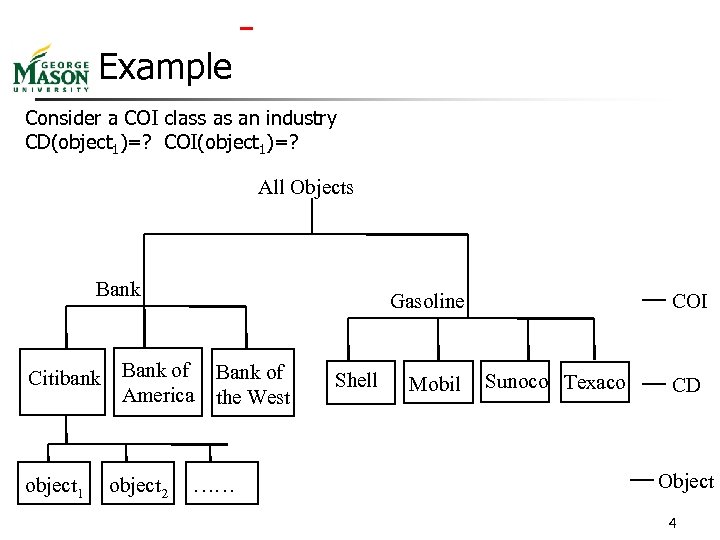
Example Consider a COI class as an industry CD(object 1)=? COI(object 1)=? All Objects Bank Citibank object 1 Gasoline Bank of America object 2 Bank of the West …… Shell Mobil COI Sunoco Texaco CD Object 4
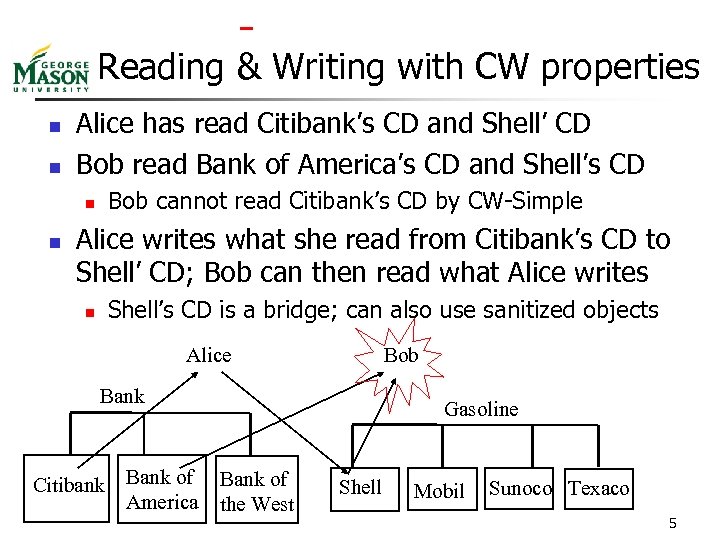
Reading & Writing with CW properties n n Alice has read Citibank’s CD and Shell’ CD Bob read Bank of America’s CD and Shell’s CD Bob cannot read Citibank’s CD by CW-Simple n n Alice writes what she read from Citibank’s CD to Shell’ CD; Bob can then read what Alice writes Shell’s CD is a bridge; can also use sanitized objects n Alice Bob Bank Citibank Bank of America Gasoline Bank of the West Shell Mobil Sunoco Texaco 5
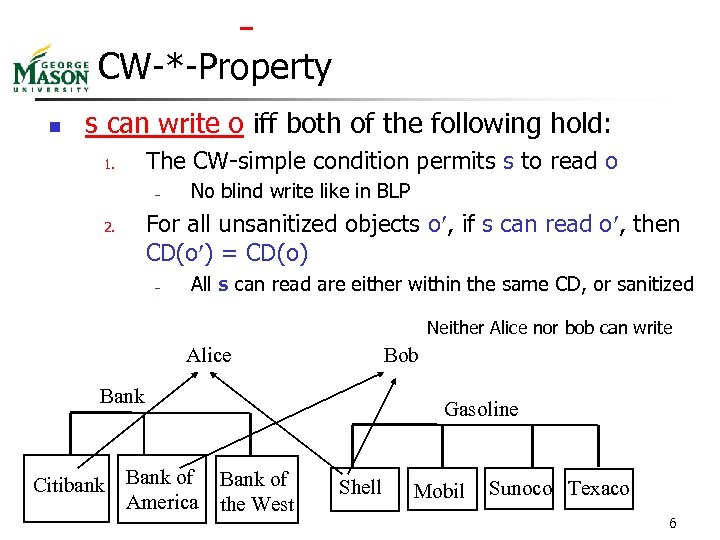
CW-*-Property n s can write o iff both of the following hold: The CW-simple condition permits s to read o 1. – No blind write like in BLP For all unsanitized objects o , if s can read o , then CD(o ) = CD(o) 2. – All s can read are either within the same CD, or sanitized Neither Alice nor bob can write Alice Bob Bank Citibank Bank of America Gasoline Bank of the West Shell Mobil Sunoco Texaco 6
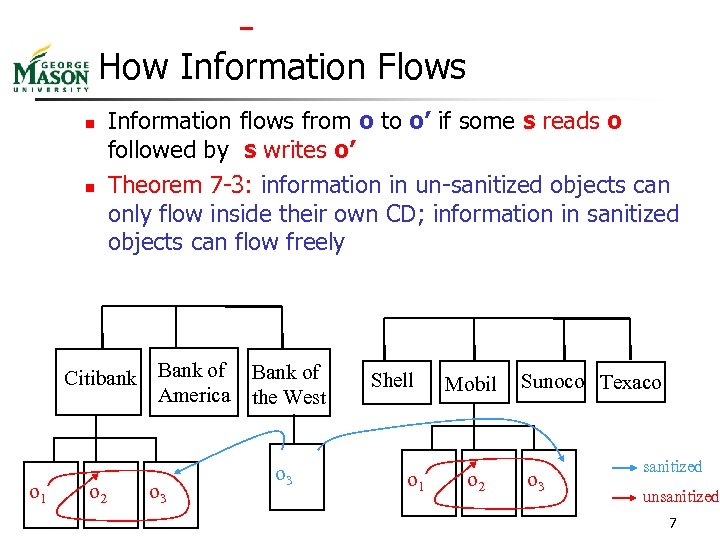
How Information Flows n n Information flows from o to o’ if some s reads o followed by s writes o’ Theorem 7 -3: information in un-sanitized objects can only flow inside their own CD; information in sanitized objects can flow freely Citibank o 1 o 2 Bank of America o 3 Bank of the West o 3 Shell o 1 Mobil o 2 Sunoco Texaco o 3 sanitized unsanitized 7

Cryptography 8

Cryptography n n n n Transposition and substitution ciphers Cesar ciphers and Vigenere ciphers Cryptanalysis Statistical analysis Block ciphers and block chaining DES and 3 DES CBC mode 9
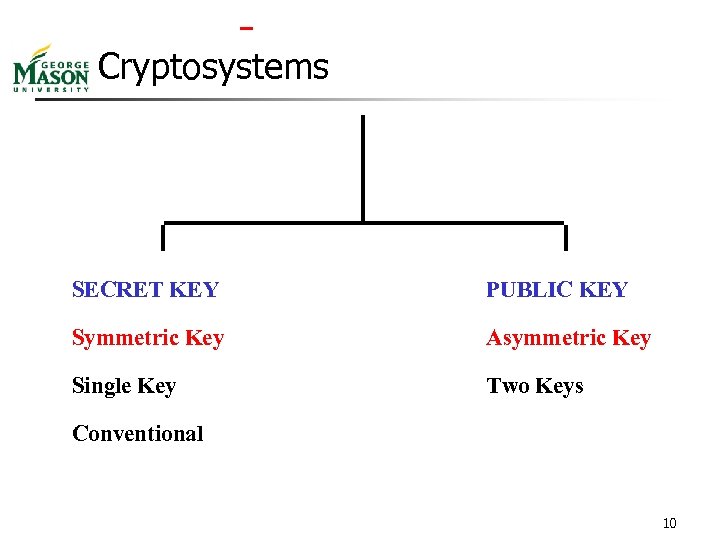
Cryptosystems SECRET KEY PUBLIC KEY Symmetric Key Asymmetric Key Single Key Two Keys Conventional 10
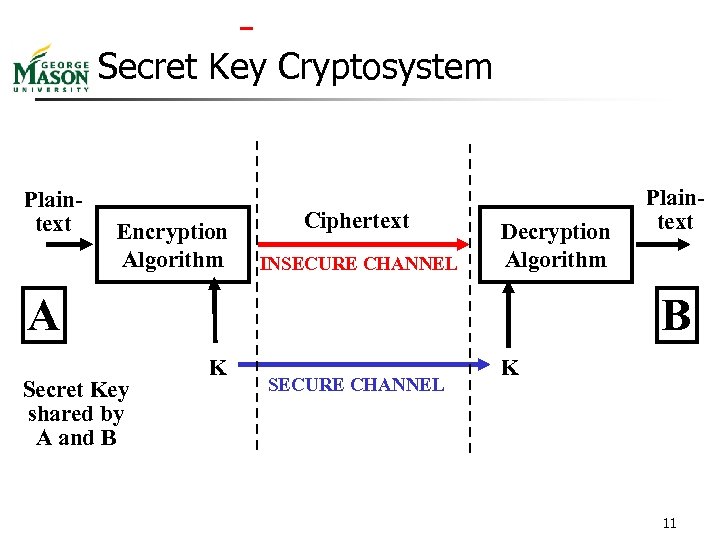
Secret Key Cryptosystem Plaintext Encryption Algorithm Ciphertext INSECURE CHANNEL Decryption Algorithm A Secret Key shared by A and B Plaintext B K SECURE CHANNEL K 11
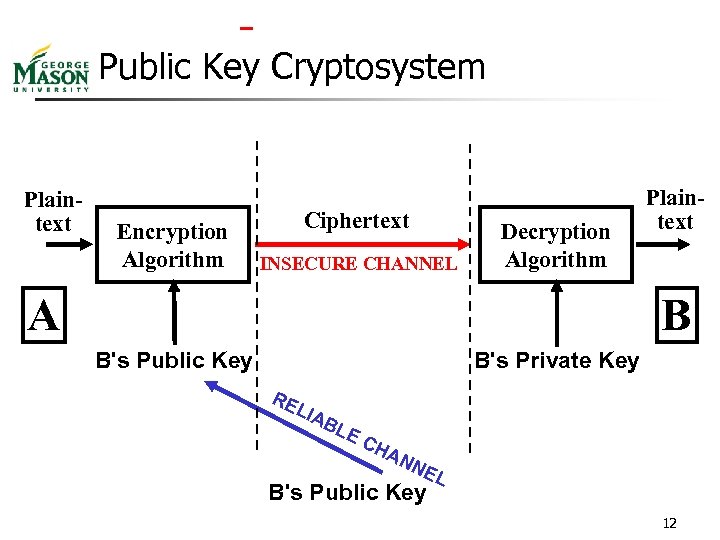
Public Key Cryptosystem Plaintext Encryption Algorithm Ciphertext INSECURE CHANNEL Decryption Algorithm A Plaintext B B's Public Key B's Private Key RE LIA BL E CH AN NE B's Public Key L 12
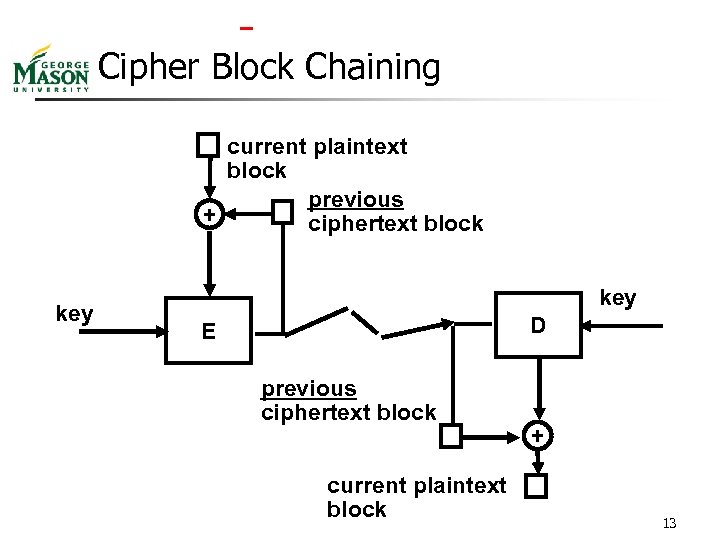
Cipher Block Chaining current plaintext block previous + ciphertext block key D E previous ciphertext block current plaintext block + 13

Overview of the DES § A product cipher § Both substitution and transposition on the bits § A block cipher: § encrypts plaintext blocks of 64 bits using a 56 bit key, and outputs 64 bits of ciphertext n n n Developed by IBM; in 1977 adopted by NIST, with NSA approval for unclassified information Also widely used by the public sector E and D are public, but the design principles are classified 14

Key Management § § § Key exchange protocols Key generation Storing and revoking keys Digital signatures Digital certificates 15

Needham-Schroeder Alice || Bob || r 1 Hey, Cathy, I need to talk to Bob. Cathy { Alice || Bob || r 1|| ks ||{ Alice || ks } k. B, C } k. A, C Alice Cathy Hey, Alice, this is your key ks is Cathy Alice And tell Bob I got him a session key ks { Alice || ks } k. B, C Hey, Bob, this is Alice. Cathy wants me to forward you a session key ks with which we can talk { r 2 } ks You’re Alice? So you must have ks. Prove it! { r 2 – 1 } ks Here’s the proof that I have ks Bob Bob 16
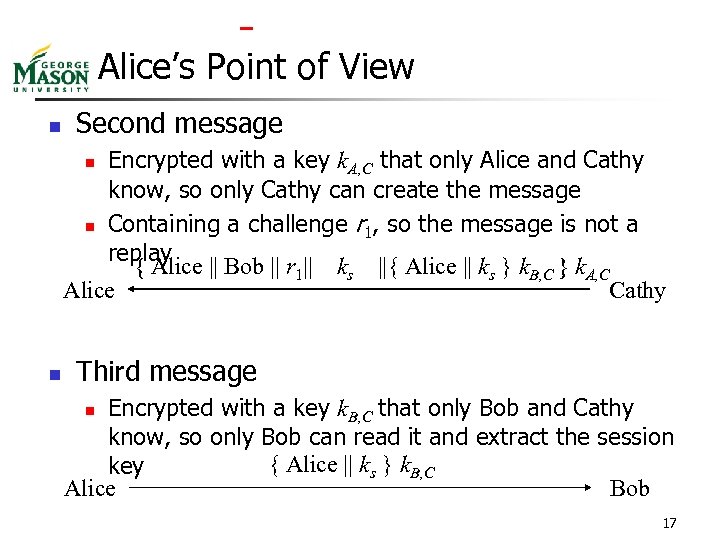
Alice’s Point of View n Second message Encrypted with a key k. A, C that only Alice and Cathy know, so only Cathy can create the message n Containing a challenge r 1, so the message is not a replay { Alice || Bob || r 1|| ks ||{ Alice || ks } k. B, C } k. A, C Alice Cathy n n Third message Encrypted with a key k. B, C that only Bob and Cathy know, so only Bob can read it and extract the session { Alice || ks } k. B, C key Alice Bob n 17
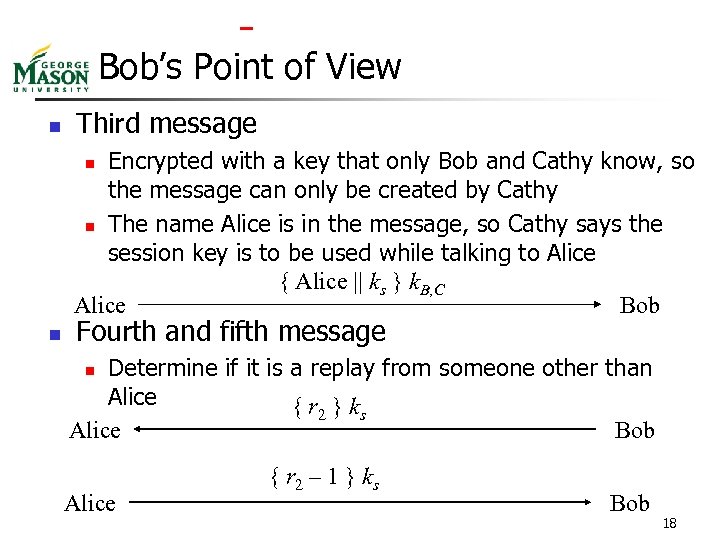
Bob’s Point of View n Third message Encrypted with a key that only Bob and Cathy know, so the message can only be created by Cathy n The name Alice is in the message, so Cathy says the session key is to be used while talking to Alice { Alice || ks } k. B, C Alice Bob n n Fourth and fifth message Determine if it is a replay from someone other than Alice { r 2 } ks Alice Bob n Alice { r 2 – 1 } ks Bob 18

Certificates n A token (message) containing n n Identity of principal (e. g. , Alice) His/her public key Timestamp (when issued) Other information (perhaps identity of issuer) signed by trusted authority (here, Cathy) CA = { e. A || Alice || T } d. C 19
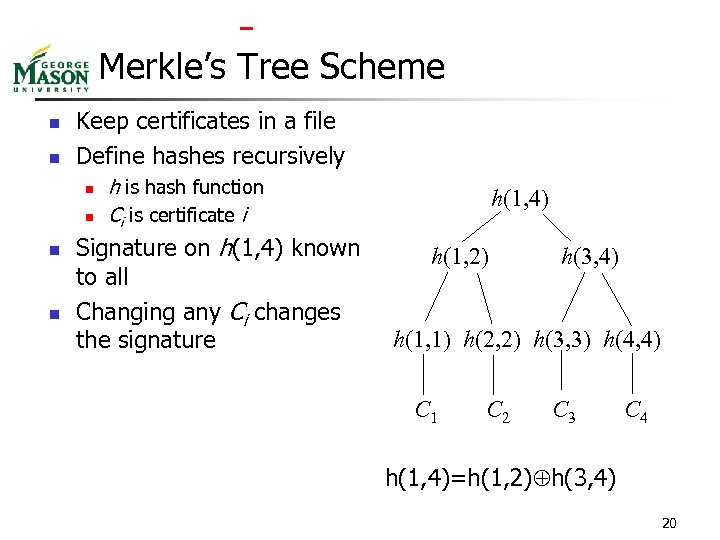
Merkle’s Tree Scheme n n Keep certificates in a file Define hashes recursively n n h is hash function Ci is certificate i Signature on h(1, 4) known to all Changing any Ci changes the signature h(1, 4) h(1, 2) h(3, 4) h(1, 1) h(2, 2) h(3, 3) h(4, 4) C 1 C 2 C 3 C 4 h(1, 4)=h(1, 2) h(3, 4) 20

Validation n h(1, 4) n The signature can be verified with any Ci To validate C 1: n h(1, 2) h(3, 4) n n n h(1, 1) h(2, 2) h(3, 3) h(4, 4) n n C 1 C 2 C 3 C 4 n Compute h(1, 1) Obtain h(2, 2) Compute h(1, 2) Obtain h(3, 4) Compute h(1, 4), signature Compare to known signature Only need to know hashes of child nodes on path 21

Cipher Techniques n n n Stream ciphers Multiple encryptions SSL and its protocols TLS IPSec 22

Diffie-Hellman Key Exchange Scheme n n n Proposed in 1976 as the first public key algorithm (predates RSA) Allows users to agree on a secret key over insecure channels with no prior communication The secret key can thus be used to encrypt or decrypt message (e. g. , SSL 3. 0, IPsec) A K Insecure Channel B 23

Discrete Logarithm Problem n D-H is based on the discrete logarithm problem n n n Given integers n and g and prime number p, compute k such that n = g k mod p In general computationally infeasible Choices for g and p are critical n n n Both p and (p– 1)/2 should be prime p should be large (at least 512 bits, possibly 1028 bits) g should be a primitive root mod p 24
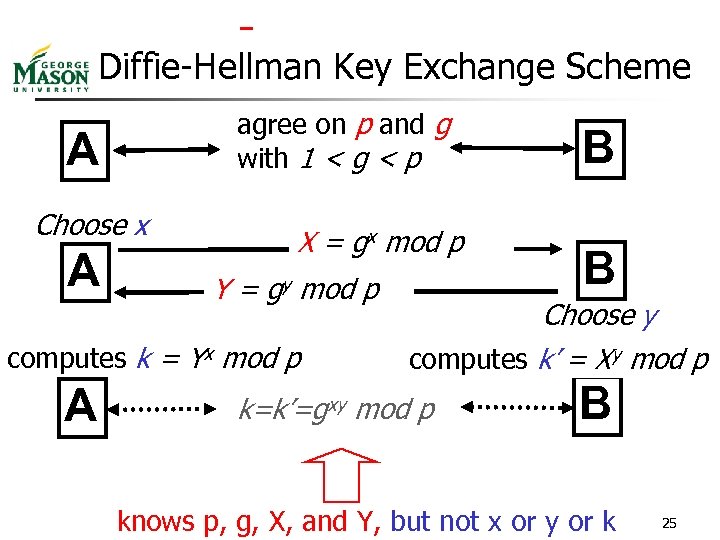
Diffie-Hellman Key Exchange Scheme agree on p and g with 1 < g < p A Choose x A X = gx mod p Y= gy mod p computes k = Yx mod p A B B Choose y computes k’ = Xy mod p k=k’=gxy mod p B knows p, g, X, and Y, but not x or y or k 25
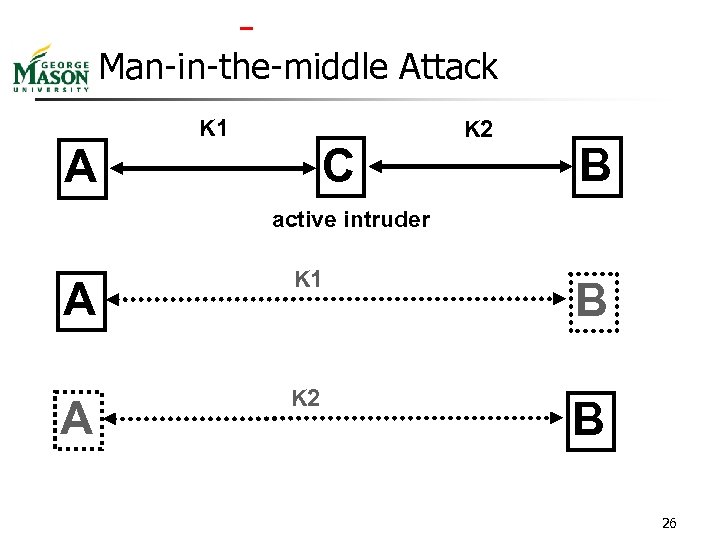
Man-in-the-middle Attack K 1 C A K 2 B active intruder A K 1 B A K 2 B 26

Authentication n n Password schemes Challenge response schemes Biometry Other forms of authentication such as recognizing photographs, solving puzzles etc. 27
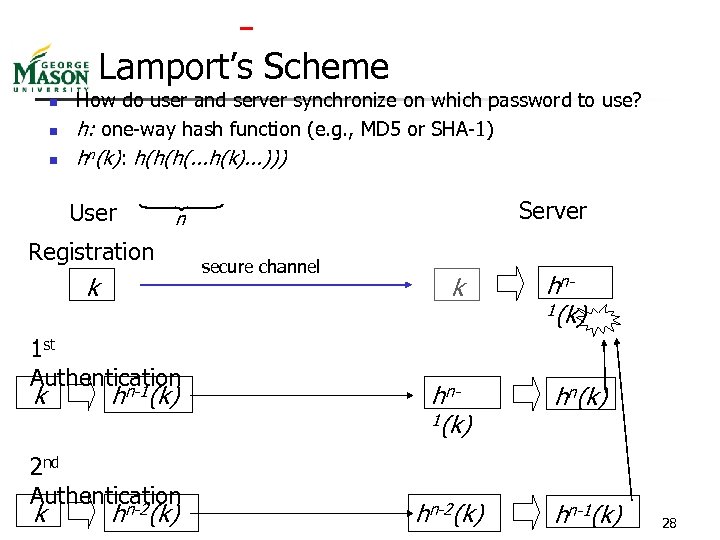
Lamport’s Scheme n n n How do user and server synchronize on which password to use? h: one-way hash function (e. g. , MD 5 or SHA-1) hn(k): h(h(h(. . . h(k). . . ))) User Registration k 1 st Authentication n-1 k h (k) 2 nd Authentication n-2 k Server n h (k) secure channel k nhn(k) 1(k) hn(k) hn-2(k) hn-1(k) 28
8a5b571ed40e0462099cf9c253e8ec85.ppt