Review Discretionary Access Control DAC Least Privilege

Review Discretionary Access Control

DAC Least Privilege Access Control Identity Assertion Role Gathering Auditing Assurance

SSH root@companion: ~# groupadd jon root@companion: ~# useradd jon -g jon -d /home/jon -s/bin/bash root@companion: ~# cd / root@companion: /# cd /home root@companion: /home# mkdir /home/jon root@companion: /home# chown jon: jon /home/jon jon@companion: ~$ ssh localhost jon@localhost's password: Welcome to Ubuntu 12. 04. 1 LTS (GNU/Linux 3. 2. 0 -30 -genericpae i 686) Requires password!!!!

No Password – How? on@companion: ~$ ssh-keygen Generating public/private rsa key pair. Enter file in which to save the key (/home/jon/. ssh/id_rsa): Enter passphrase (empty for no passphrase): Your public key has been saved in /home/jon/. ssh/id_rsa. pub. jon@companion: ~$ ls -al. ssh total 20

We ssh now jon@companion: ~$ ssh localhost Welcome to Ubuntu 12. 04. 1 LTS (GNU/Linux 3. 2. 0 -30 -generic-pae i 686) * Documentation: https: //help. ubuntu. com/ Let's us in without a password!!!

Look at this a little further jon@companion: ~/. ssh$ more id_rsa -----BEGIN RSA PRIVATE KEY----MIIEow. IBAAKCAQEA 1/O 96 EGofj. J/fd. Bv. F 5 VVIi. G tn. Ce. Lgc+Ygt 0 XIv/N 3 M 9 lm. CLN 9 m 6 TGk. Jgn 9 Azrd. VREb+R 93 i 0 D 4 Tvpv/kufd 3 LP 9 jo. AWPHIo. FIEq 6 r. Rsrhj 1 U 4 qnb jon@companion: ~/. ssh$ more authorized_keys ssh-rsa AAAAB 3 Nza. C 1 yc 2 EAAAADAQABAAABAQDX 873 o. Qah+Mn 990 G 8 Xl. VUi. Ia 2 c. J 4 u. Bz 5 i. C 3 Rci/8

SSH With Passphrase jon@companion: ~$ ssh-keygen Generating public/private rsa key pair. Enter file in which to save the key (/home/jon/. ssh/id_rsa): Enter passphrase (empty for no passphrase): lakers Enter same passphrase again: lakers jon@companion: ~/. ssh$ mv id_rsa. pub authorized_keys jon@companion: ~/. ssh$ ssh localhost

What is encryption? A process that converts original information, also called plain text into a difficult-to-interpret form called ciphertext. Done by using an encryption algorithm, a formula used to turn plain text into ciphertext. Two types: Asymmetric and Symmetric

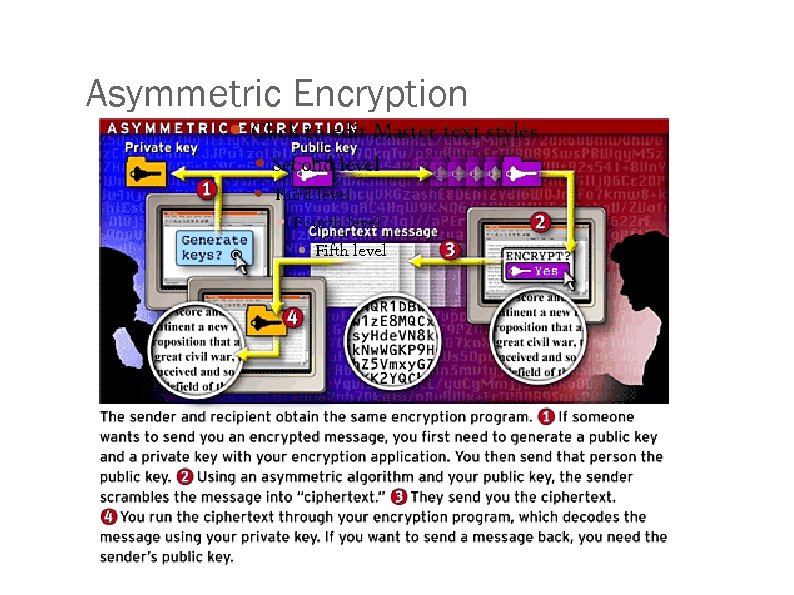Asymmetric Encryption Click to edit Master text styles Second level Third level Fourth level Fifth level

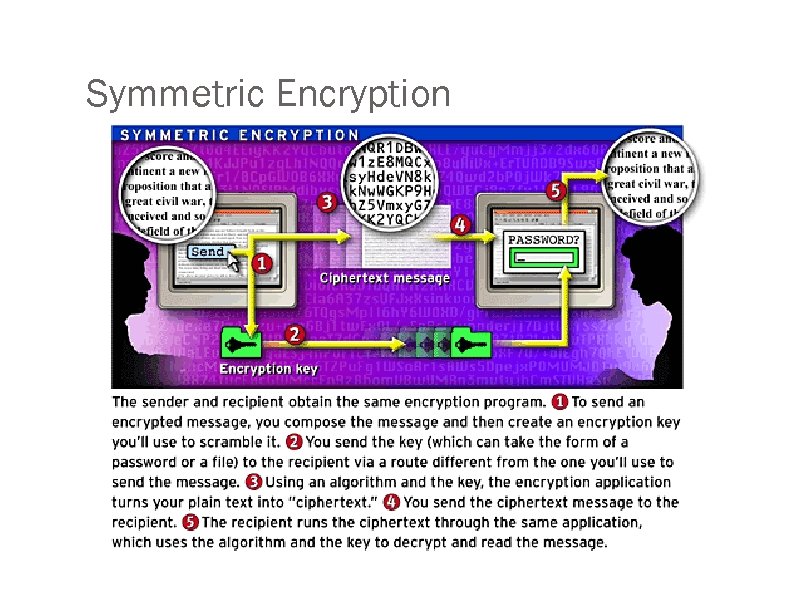Symmetric Encryption

Which one is better? Although, symmetric encryption is fast, it is not as safe as asymmetric encryption because someone could “steal” the key and decode the messages. But because of its speed, it's commonly used for e-commerce transactions. Asymmetric encryption is more complex--and more secure. Asymmetric encryption's added safety comes at a price: More computation is required, so the process takes longer. (several orders or magnitude longer)

Who’s using encryption? If you use a computer and the internet, you’re using encryption! Enables all organizations regardless of their size, to be both user-and -IT friendly.

Why use encryption? Authentication Protects personal data such as passwords. Privacy – Provides for confidentiality of private information. Integrity – Ensures that a document or file has not been altered. Accountability Prevents denial or plagiarism.

Examples of Encryption Web browser encryption Email encryption Hard drive encryption Operating system protection

What is cryptography? “hidden writing” Until recently: military tool Like any military technology: methods change over time Two sides: designing codes breaking codes (cryptanalysis) Computers have changed both

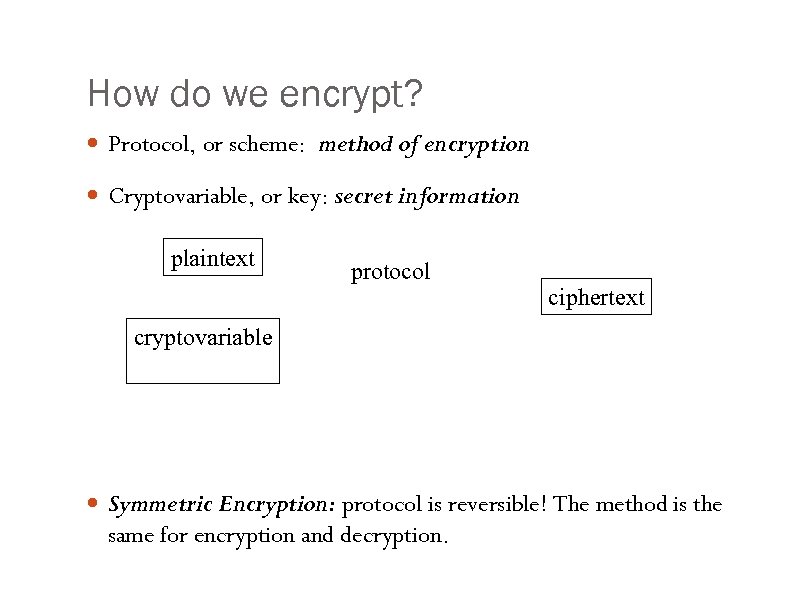How do we encrypt? Protocol, or scheme: method of encryption Cryptovariable, or key: secret information plaintext protocol ciphertext cryptovariable Symmetric Encryption: protocol is reversible! The method is the same for encryption and decryption.

Example: Caesar Shift Protocol: shift each letter by the same amount Cryptovariable: amount to shift IBM HAL -1 Veni, vidi, vici Foxs, fsns, fsms Decryption: shift back the same amount

Substitution Cipher • Allow any permutation of the alphabet • Key = permutation; 26! possibilities • 26! = 403, 291, 461, 126, 605, 635, 584, 000 • Roughly 288: checking 1 billion per second, would take 12 billion years • Is there a better way? • al-Kindi, ninth century: frequency analysis

A harder example YIRLAZ MRACIRB CR PKORI CRP: MRPPVAMQAY MRLACZRGA, VAYQAVW RA • Shorter = less information • R occurs 10 times, A occurs 9 times – (all others occur 4 or fewer times) • Telegraph style; fewer short words

A harder example E E E YIRLAZ MRACIRB CR PKORI CRP: E E MRPPVAMQAY MRLACZRGA, VAYQAVW RA E doesn’t begin any common 2 -letter words

A harder example O O O YIRLAZ MRACIRB CR PKORI CRP: O O MRPPVAMQAY MRLACZRGA, VAYQAVW RA A occurs 9 times. What could it be?

A harder example O N ON O O YIRLAZ MRACIRB CR PKORI CRP: O N N N ON MRPPVAMQAY MRLACZRGA, VAYQAVW RA

A harder example O N ONT O TO YIRLAZ MRACIRB CR PKORI CRP: O N N O NT O N N N ON MRPPVAMQAY MRLACZRGA, VAYQAVW RA

A harder example G O N ONT O TO YIRLAZ MRACIRB CR PKORI CRP: O N ING O NT O N NGIN ON MRPPVAMQAY MRLACZRGA, VAYQAVW RA

A harder example GROUND CONTROL TO MAJOR TOM: YIRLAZ MRACIRB CR PKORI CRP: COMMENCING COUNTDOWN, ENGINES ON MRPPVAMQAY MRLACZRGA, VAYQAVW RA

The perfect cryptosystem • One-time pad: encrypt each letter with its own key • Example: Caesar shift each letter separately • Ci = Pi + Ki (mod 26) • To encrypt n bits, use n bits of key • This uses up lots of key bits; need to prearrange • How do you generate key bits?

Enigma Machine • German cryptosystem in World War II • Same idea: modify letters • Scrambler disks implement permutation • Rotate after each letter, so many different permutations used • Additional permutation provided by plugboard

Enigma Key changed daily 3 scramblers in one of 6 orders In 1938: 3 of 5, so 60 arrangements 263 = 17, 576 settings for scramblers Billions of plugboard settings Alan Turing: bypassed plugboard Used known plaintext, exhausted over space British were able to read traffic

Navajo Code Talkers Americans in the Pacific during WWII Each troop had one Navajo Even after figuring out system, Japanese couldn’t break it Like a one-time pad: prearranged secret is a whole language May not be feasible today

Modern Symmetric Cryptography Assume the protocol is known to the enemy Only the key is secret Encryption, cryptanalysis use computers Operate on bits, rather than letters DES, AES Open standards; let everyone try to break it Closed design often fails (cell phones) Don’t try this in-house

Key Distribution Secure communication requires a key How do you exchange keys securely? Military: codebooks in field could fall into enemy hands Commerce: might not meet face-to-face Seems to be a Catch-22

Paradigm Shift Alice wants to mail Bob a letter securely If they share a “key”, Alice locks, Bob unlocks If not: Alice puts on padlock, sends box to Bob adds his padlock, sends box back to Alice removes her padlock, sends box to Bob unlocks box, reads letter Problem: how to translate this to mathematics

Diffie-Hellman-Merkle (1976) Modular Arithmetic Choose Y, modulus p Alice’s function is YA (mod p) Bob’s function is YB (mod p) Key is YAB = YBA (mod p) Eve can’t compute YAB from Y, YA, YB We think (no one can prove it) One problem: must communicate to get key

One-way Functions • Easy to compute, hard to reverse • Example: f (A) = YA (mod p) • f -1(YA) is called “discrete log” • Hard to compute (we think) • Could always do exhaustive search • Here, there are p-1 choices

Cryptographic Primitives • Building blocks for algorithms • Example: one-way functions • Protocols built out of primitives • Example: Diffie-Hellman-Merkle • Protocols built out of other protocols • Example: • 1. Use Diffie-Hellman to exchange key • 2. Use symmetric encryption, key to encode message • Good, “modular” design

Trapdoor one-way functions • Another useful primitive • f (X) is easy to compute • f -1(Y) is hard for most people to compute • But: easy to compute if you know a secret • There are trapdoor one-way functions • Found by Rivest-Shamir-Adleman, 1977 • Rely on difficulty of factoring large integers

Idea behind public key • Bob publishes design specs for a padlock • Alice wants to send Bob a box • Alice builds a Bob padlock, locks the box • Bob unlocks box using his key • Eve intercepts box, knows design specs • Goal: Eve still can’t build a key • Padlock = trapdoor one-way function

Public Key Cryptography • Alice wants to talk to Bob: computes key X • Alice sends Bob f. B (X) (Bob’s function) • Bob computes f. B-1 (f. B (X)) = X • Both Alice and Bob know X, use as key for symmetric encryption • Eve knows f. B (X); can’t compute X • Asymmetric encryption • Whitfield Diffie, 1975

RSA: Choosing Keys • Choose two large prime numbers p, q. (e. g. , 1024 bits each) • Compute n = pq, z = (p-1)(q-1) • Choose e (with e

RSA: Encryption, decryption • Given (n, e) and (n, d) as computed before • To encrypt bit pattern, m, compute: • c = me mod n • To decrypt received bit pattern, c, compute • m = cd mod n

RSA example • Bob chooses p=5, q=7. Then n=35, z=24. • e=5 (so e, z relatively prime). • d=29 (so ed-1 exactly divisible by z. encrypt: decrypt: e letter m m l 12 1524832 c 17 c d 48196857210675091411825223071697 c = me mod n 17 m = cd mod n 12 letter l

Digital Signature Scheme • Alice wants to send Bob a message, sign it • Alice sends Bob X and S = f. A-1 (X) • Bob checks that f. A (S) = X • Therefore Bob knows that S = f. A-1 (X) • Only Alice can compute f. A-1 (X) easily, so Alice must have sent the message • Same primitive, new protocol

Revolution • New ideas made cryptography an option for commerce • PCs gave everyone computing power • Zimmerman’s PGP: gave everyone access • SSL in web browsers

Quantum Computation • Computers revolutionized cryptographic design and cryptanalysis • Quantum computers may one day do the same • Quantum key exchange: guaranteed secure • A quantum computer could factor large integers in polynomial time • We may never live to see one

Symmetric Cryptography DES (Data Encryption Standard) • US encryption standard [NIST 1993] • 56 -bit symmetric key, 64 -bit plaintext input • How secure is DES? • DES Challenge: 56 -bit-key-encrypted phrase (“Strong cryptography makes the world a safer place”) decrypted (brute force) in 4 months • no known “backdoor” decryption approach • making DES more secure: • use three keys sequentially (3 -DES) on each datum • use cipher-block chaining

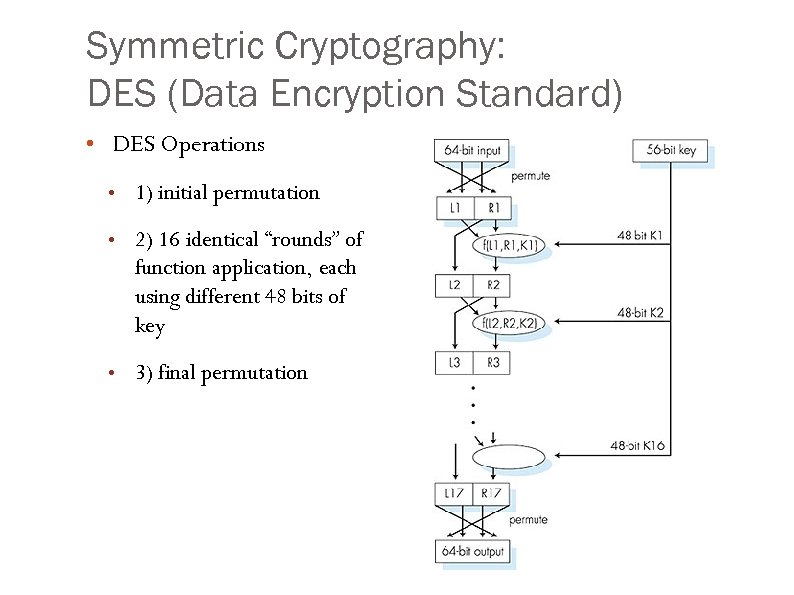Symmetric Cryptography: DES (Data Encryption Standard) • DES Operations • 1) initial permutation • 2) 16 identical “rounds” of function application, each using different 48 bits of key • 3) final permutation

Symmetric Cryptography: AES (Advanced Encryption Standard) • new (Nov. 2001) symmetric-key NIST standard, replacing DES • processes data in 128 bit blocks • 128, 192, or 256 bit keys • brute force decryption (try each key) taking 1 sec on DES, takes 149 trillion years for AES

Trusted Intermediaries • Symmetric key problem: • How do two entities establish shared secret key over network? • trusted key distribution center (KDC) acting as intermediary between entities • Public key problem: • When Alice obtains Bob’s public key (from web site, e-mail, diskette), how does she know it is Bob’s public key, not Trudy’s? • trusted certification authority (CA)

Certification Authorities • Certification authority (CA): binds public key to particular entity, E. • E (person, router) registers its public key with CA • E provides “proof of identity” to CA. • CA creates certificate binding E to its public key. • certificate containing E’s public key digitally signed by CA – CA says “this is E’s public key” • When Alice wants Bob’s public key: • gets Bob’s certificate (Bob or elsewhere). • apply CA’s public key to Bob’s certificate, get Bob’s public key

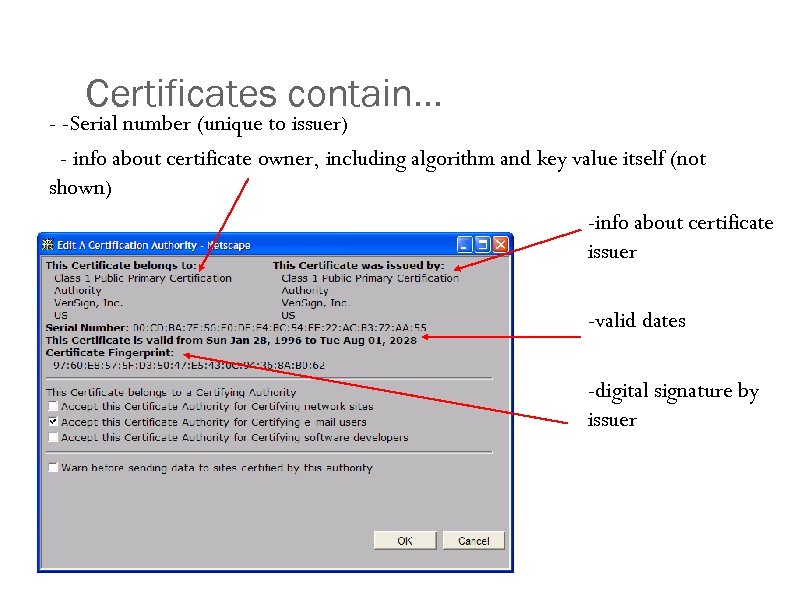Certificates contain… - -Serial number (unique to issuer) - info about certificate owner, including algorithm and key value itself (not shown) -info about certificate issuer -valid dates -digital signature by issuer

Pretty good privacy (PGP) • Internet e-mail encryption scheme, defacto standard. • uses symmetric key cryptography, public key cryptography, hash function, and digital signature as described. • provides secrecy, sender authentication, integrity. • inventor, Phil Zimmerman, was target of 3 -year federal ---BEGIN PGP SIGNED MESSAGE--Hash: SHA 1 Bob: My husband is out of town tonight. Passionately yours, Alice ---BEGIN PGP SIGNATURE--Version: PGP 5. 0 Charset: noconv yh. HJRHh. GJGhgg/12 Ep. J+lo 8 g. E 4 v. B 3 mq. Jh. FEv ZP 9 t 6 n 7 G 6 m 5 Gw 2 ---END PGP SIGNATURE---

Secure sockets layer (SSL) • transport layer security to any TCP-based app using SSL services. • used between Web browsers, servers for e-commerce • security services: • server authentication • data encryption • client authentication (optional) server authentication: • • • Browser requests server certificate, issued by trusted CA. • • SSL-enabled browser includes public keys for trusted CAs. Browser uses CA’s public key to extract server’s public key from certificate. check your browser’s security menu to see its trusted CAs .

Secure sockets layer (SSL) • SSL may be one way encrypted – https • Or it may be two way encrypted which is • Https with a certificate (private key). • The certificate (PKI) is used for identity assertion.

IEEE 802. 11 security • War-driving: drive around Bay area, see what 802. 11 networks available? • More than 9000 accessible from public roadways • 85% use no encryption/authentication • packet-sniffing and various attacks easy! • Securing 802. 11 • encryption, authentication • first attempt at 802. 11 security: Wired Equivalent Privacy (WEP): a failure • current attempt: 802. 11 i

Lab Take a file and encrypt is using crypt from Unix. Use a four letter key. Type: sudo apt-get install mcrypt man crypt google crypt ubuntu encrypt a file Command: echo “hello world” > text. txt Command crypt taking text. txt making text. cipher Command taking text. cipher get back to text. orig Plaintext ---- > cipher ------> Plaintext

Lab Answers cat hello. txt | crypt > hello. txt. cipher crypt < hello. txt. cipher

Second Lab Take a file and encrypt it using des from Unix. Use a four letter key. Decrypt the same file and prove it works. This is symmetric. Plaintext ----> Cipher that is DES -----> Plaintext.

Second Lab Answer crypt < hello. txt. cipher cat hello. txt | mcrypt -a des > hello. txt. cipher mcrypt -a des -d < hello. txt. cipher > x