d797d4ff3496c1e150a1cda49fe5267b.ppt
- Количество слайдов: 19

Resource Allocation in Heterogeneous Computing Systems By Chris Klumph and Kody Willman Advisor: Professor H. J. Siegel 1

Resource allocation in a MMOG in a massive multiplayer online game (MMOG) multiple users are simultaneously connected at any given time a heterogeneous system includes varying computer capabilities varying communication times need to implement resource allocation heuristics for this heterogeneous system 2
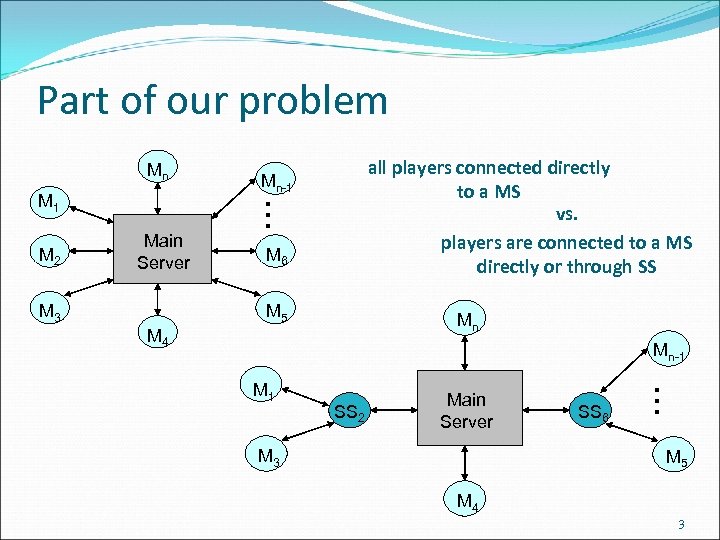
Part of our problem Mn M 2 … M 1 all players connected directly to a MS vs. players are connected to a MS directly or through SS Mn-1 Main Server M 3 M 6 M 5 Mn M 4 Mn-1 SS 2 Main Server M 3 SS 6 … M 1 M 5 M 4 3

Goal of Project and Terminology Goal Terminology given 200 players are directly connected to MS need to create different heuristics distribute the 200 players between MS and SS So RTmax time is as low as possible RTmax the maximum communication time between computers and MS heuristic way to allocate resources chromosome mapping of a possible solution of players and SS 4

For this problem Chris has worked on Genitor heuristic Kody has worked on Min-Min heuristic 5

Genitor Overview Genitor_matching_scheduling { initial_population_generation; ranking; while(stopping criteria not met) { selection; crossover; mutation; ranking; } output best solution found; } selection – selects 2 random parents in the hope of duplicating better chromosomes crossover – picks 2 random points within chromosomes, and swaps data points in between points mutation –randomly mutate elements within chromosomes ranking – determines which chromosome represents the best solution found, inserts into ranked list stopping criteria – 10, 000 iterations with no change in best solution or 10 minutes 6
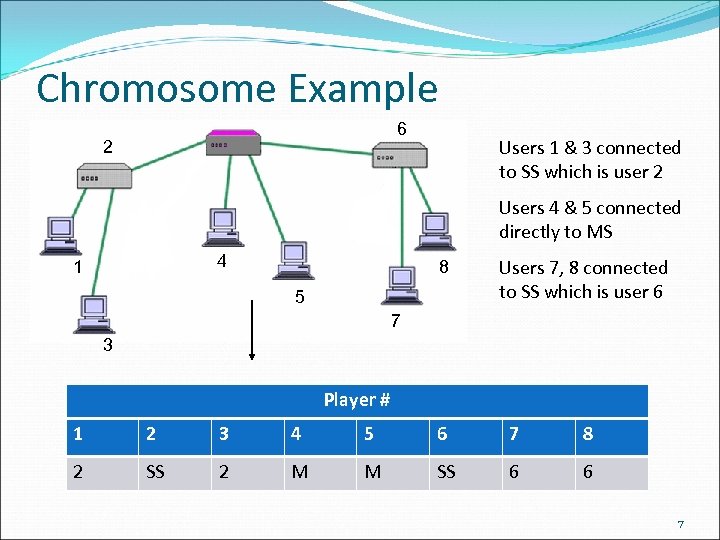
Chromosome Example 6 2 Users 1 & 3 connected to SS which is user 2 Users 4 & 5 connected directly to MS 4 1 8 5 Users 7, 8 connected to SS which is user 6 7 3 Player # 1 2 3 4 5 6 7 8 2 SS 2 M M SS 6 6 7
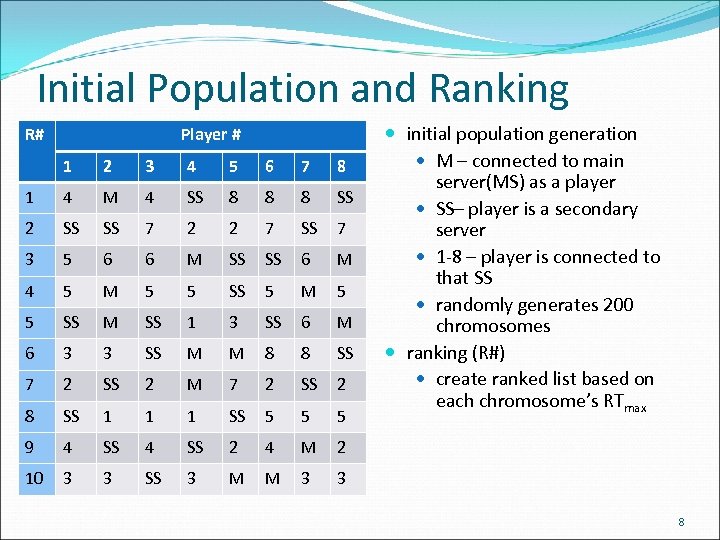
Initial Population and Ranking R# Player # 1 2 3 4 5 6 7 8 1 4 M 4 SS 8 8 8 SS 2 SS SS 7 2 2 7 SS 7 3 5 6 6 M SS SS 6 M 4 5 M 5 5 SS M SS 1 3 SS 6 M 6 3 3 SS M M 8 8 SS 7 2 SS 2 M 7 2 SS 2 8 SS 1 1 1 SS 5 5 5 9 4 SS 2 4 M 2 10 3 3 SS 3 M M 3 initial population generation M – connected to main server(MS) as a player SS– player is a secondary server 1 -8 – player is connected to that SS randomly generates 200 chromosomes ranking (R#) create ranked list based on each chromosome’s RTmax 3 8
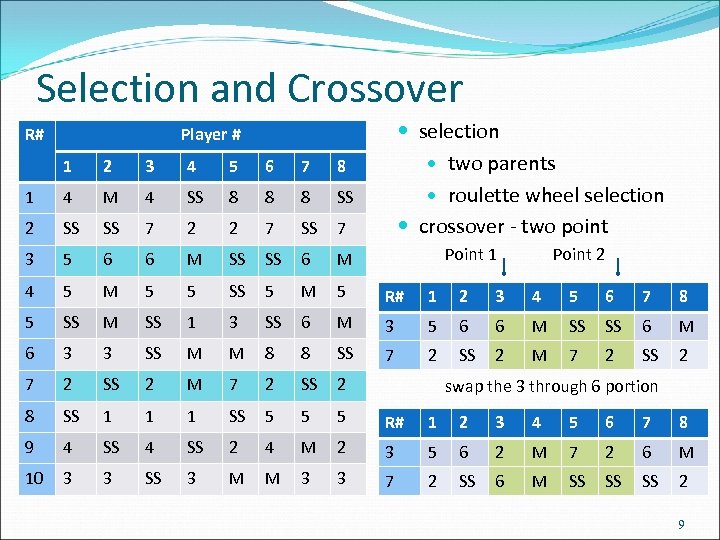
Selection and Crossover R# selection two parents roulette wheel selection crossover - two point Player # 1 2 3 4 5 6 7 8 1 4 M 4 SS 8 8 8 SS 2 SS SS 7 2 2 7 SS 7 3 5 6 6 M SS SS 6 M 4 5 M 5 5 SS 5 M 5 R# 1 2 3 4 5 6 7 8 5 SS M SS 1 3 SS 6 M 3 5 6 6 M SS SS 6 M 6 3 3 SS M M 8 8 SS 7 2 SS 2 M 7 2 SS 2 8 SS 1 1 1 SS 5 5 5 R# 1 2 3 4 5 6 7 8 9 4 SS 2 4 M 2 3 5 6 2 M 7 2 6 M 10 3 3 SS 3 M M 3 3 7 2 SS 6 M SS SS SS 2 Point 1 Point 2 swap the 3 through 6 portion 9
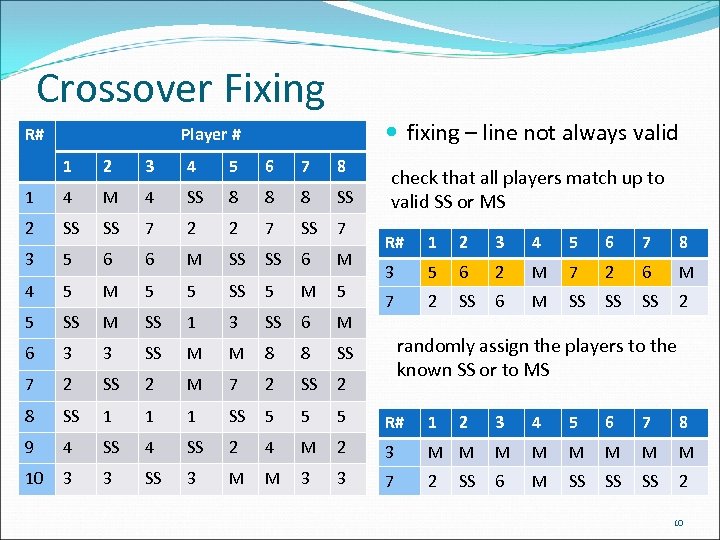
Crossover Fixing R# fixing – line not always valid Player # 1 2 3 4 5 6 7 8 1 4 M 4 SS 8 8 8 SS 2 SS SS 7 2 2 7 SS 7 3 5 6 6 M SS SS 6 M 4 5 M 5 5 SS M SS 1 3 SS 6 M 6 3 3 SS M M 8 8 SS 7 2 SS 2 M 7 2 SS 2 8 SS 1 1 1 SS 5 5 5 R# 1 9 4 SS 2 4 M 2 3 10 3 3 SS 3 M M 3 3 7 check that all players match up to valid SS or MS R# 1 2 3 4 5 6 7 8 3 5 6 2 M 7 2 6 M 7 2 SS 6 M SS SS SS 2 randomly assign the players to the known SS or to MS 2 3 4 5 6 7 8 M M M M 2 6 M SS SS SS 2 SS 10
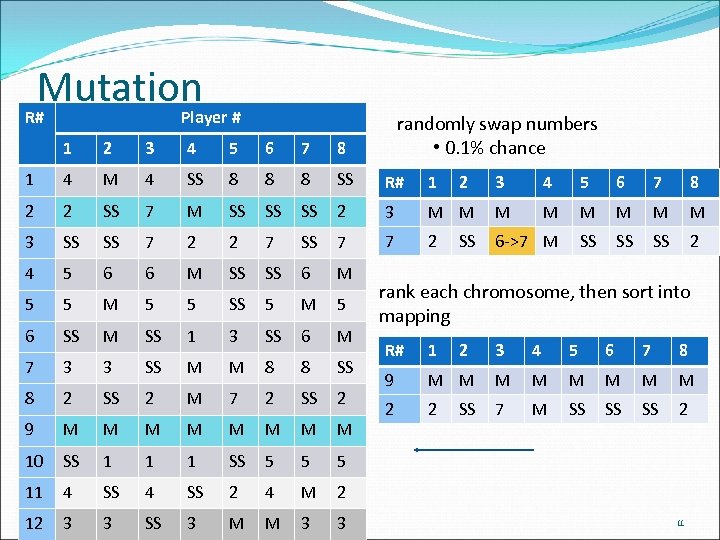
Mutation R# R# 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 11 1 1 4 4 2 SS SS 5 5 SS SS 3 3 2 2 SS M 4 SS 3 4 2 2 M M SS SS SS 6 6 M M 3 3 SS SS 1 M SS 1 3 SS 3 3 4 4 7 7 7 6 6 5 5 SS SS 2 2 1 M 4 1 SS 4 12 3 3 SS Player # 4 5 SS 8 M SS 2 2 M SS 5 SS 1 3 M M M 7 1 SS M M SS 2 1 SS 3 M SS 2 3 M 6 6 8 8 SS 7 7 SS SS 5 5 SS SS 8 8 2 2 5 M 4 7 7 8 8 SS SS SS 6 6 M M 6 6 8 8 SS SS 5 M M 5 3 M 8 8 SS SS 2 7 7 M M 5 5 M M SS SS 2 2 5 M 2 5 3 2 M 3 3 randomly swap numbers • 0. 1% chance R# 1 3 7 2 3 4 5 6 7 8 M M M M 2 6 ->7 M SS SS SS 2 SS rank each chromosome, then sort into mapping R# 1 9 2 2 3 4 5 6 7 8 M M M M 2 7 M SS SS SS 2 SS 11
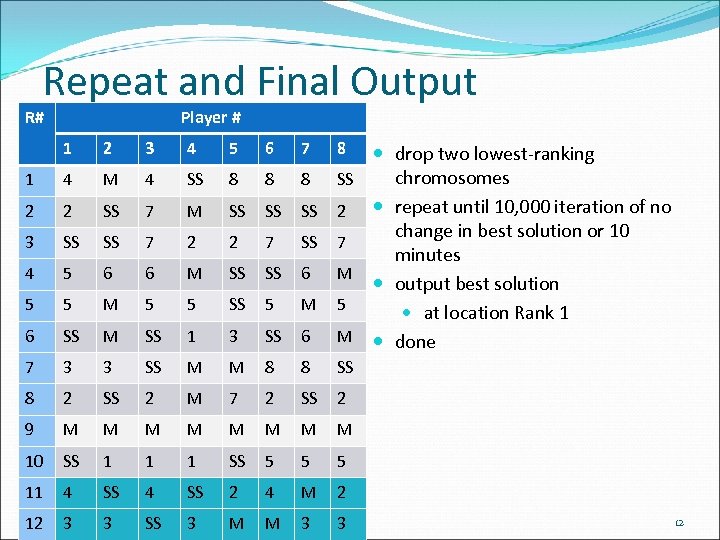
Repeat and Final Output R# R# 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 11 1 1 4 4 2 2 SS SS 5 5 SS SS 3 3 2 2 M M SS SS 4 2 2 M M SS SS 6 6 M M 3 3 SS SS M M 1 1 SS 3 3 4 4 7 7 6 6 5 5 SS SS 2 2 M M 1 1 4 12 3 3 SS Player # 4 5 SS 8 M SS 2 2 M SS 5 SS 1 3 M M M 7 M M 1 SS SS 2 3 M 6 6 8 8 SS SS 7 7 SS SS 5 5 SS SS 8 8 2 2 M M 5 5 4 7 7 8 8 SS SS 6 6 M M 6 6 8 8 SS SS M M 5 5 M 8 8 SS SS 2 2 7 7 M M 5 5 M M SS SS 2 2 M M 5 5 2 M 3 3 drop two lowest-ranking chromosomes repeat until 10, 000 iteration of no change in best solution or 10 minutes output best solution at location Rank 1 done 12

Min-Min Overview considering all unmapped tasks while(there are unmapped tasks) { find task with single overall minimum computation plus connection time; assign task to corresponding machine; update machines and computation and connection times; } have 200 players or tasks run a greedy Min-Min (used as base comparison) run Phase 1 run Phase 2 compare completion times output best solution 13

Min-Min Introduction P# 1 2 3 4 5 6 7 8 9 10 Type UP UP UP no players connected to MS, find player with minimum only SS connection plus computation 3 types of players time UP – unmapped player connect player SS – secondary servers update connection and M – mapped to MS computation times 1 -10 – player mapped to repeat for all unmapped players that SS P# 1 2 3 4 5 6 7 8 9 10 Type 6 M 7 7 SS SS SS 6 6 5 14
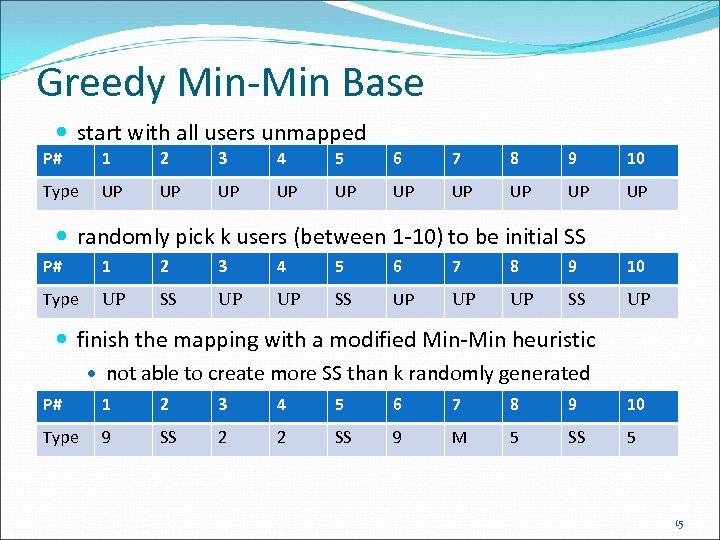
Greedy Min-Min Base start with all users unmapped P# 1 2 3 4 5 6 7 8 9 10 Type UP UP UP randomly pick k users (between 1 -10) to be initial SS P# 1 2 3 4 5 6 7 8 9 10 Type UP SS UP UP UP SS UP finish the mapping with a modified Min-Min heuristic not able to create more SS than k randomly generated P# 1 2 3 4 5 6 7 8 9 10 Type 9 SS 2 2 SS 9 M 5 SS 5 15

Phase 1 implementation find the user with the largest RTmax P# 1 2 3 4 5 6 7 8 9 10 Type 9 SS 2 2 SS 9 M 5 SS 5 if user is SS or M no other players connected remap as player connected to SS with a better RTmax if user is connect to SS remap as player to different SS with better connection time or remap as SS with better connection time P# 1 2 3 4 5 6 7 8 9 10 Type 9 SS 2 2 SS 2 M 5 SS 5 repeat for 1000 iterations or no update 16

Phase 2 set up start with the end mapping from Phase 1 find the set of all the SS from the set of SS find the SS with the largest α α is highest computation plus highest communication p is the number of players connected to that SS µ is the computational constant for that SS Comm(SS, MS) is the communication time from SS to the MS α = (p)² x µ + 2 x Comm(SS, MS) P# 1 2 3 4 5 6 7 8 9 10 Type 9 SS 2 2 SS 2 M 5 SS 5 17

Phase 2 implementation try swapping all mapped players into the set of SS in the α SS location remap with the modified Min-Min P# 1 2 3 4 5 6 7 8 9 10 Type 9 SS 2 2 SS 9 M 5 SS 5 if mapped player gives a better round trip time make that mapped player a SS P# 1 2 3 4 5 6 7 8 9 10 Type 9 3 SS 9 M 5 SS 5 repeat 1000 iterations or no improvement output best solution 18

Future Work continue to modify current heuristics to get better results could possibly implement other types of heuristics consider making it a dynamic application where players can join, play, and then leave budget have not needed to buy equipment or programs still have full budgeted amount of $100 sponsors no sponsors currently Questions? 19
d797d4ff3496c1e150a1cda49fe5267b.ppt