Resolution III Designs Designs with main effects

Resolution III Designs • Designs with main effects aliased with twofactor interactions • Used for screening (5 – 7 variables in 8 runs, 9 - 15 variables in 16 runs, for example) • A saturated design has k = N – 1 variables • See Table 8 -19, page 313 for a 1

Resolution III Designs Complete defining relation I = ABD = ACE = BCF = ABCG = BCDE = ACDF = CDG = ABEF = BEG = AFG = DEF = ADEG = CEFG = BDFG = ABCDEFG The aliases of an effect (e. g. B) B = AD = ABCE = CF = ACG = CDE = ABCDF = BCDG = AEF = EG = ABFG = BDEF = ABDEG = BCEFG = DFG = ACDEFG 2

Resolution III Designs • dof = N – 1 = 7 (used to estimate 7 main effects) • Assuming three and higher order interactions are negligible • Saturated resolution III design can be used to obtain resolution III designs with fewer factors e. g. by dropping one column (e. g. column G) Complete defining relation I = ABD = ACE = BCF = ABCG = BCDE = ACDF = CDG = ABEF = BEG = AFG = DEF = ADEG = CEFG = BDFG = ABCDEFG 3

Resolution III Designs • Dropping several factors in the defining relation to form a new design. E. g. drop B, D, F and G I = ABD = ACE = BCF = ABCG = BCDE = ACDF = CDG = ABEF = BEG = AFG = DEF = ADEG = CEFG = BDFG = ABCDEFG • It’s possible to form a 23 design with A, B, and C • Care is needed to form the best design 4

Resolution III Designs • Sequential assembly of fractions to separate aliased effects by combining designs generated by switching certain signs – fold over • Switching the signs in one column provides estimates of that factor and all of its two-factor interactions • Switching the signs in all columns de-aliases all main effects from their two-factor interaction alias chains – called a full fold-over/reflection 5

Resolution III Designs • Defining relation for a fold-over design – Each separate fraction has L + U words as generators, and the combined design will have L + U – 1 words as generators, where • L: words of like sign • U-1: words of independent even products of the words of unlike sign • Example – First fraction: I=ABD, I=ACE, I=BCF, and I=ABCG – Second fraction: I=-ABD, I=-ACE, I=-BCF, and I=ABCG – L=1, U=3, L+U=4 – Combined design: L+U-1=3 generators I=ABCG, I=(ABD)(ACE)=BCDE, I=(ABD)(BCF)=ACDF – Complete defining relation I=ABCG=BCDE=ACDF=ADEG=BDFG=ABEF=CEFG 6

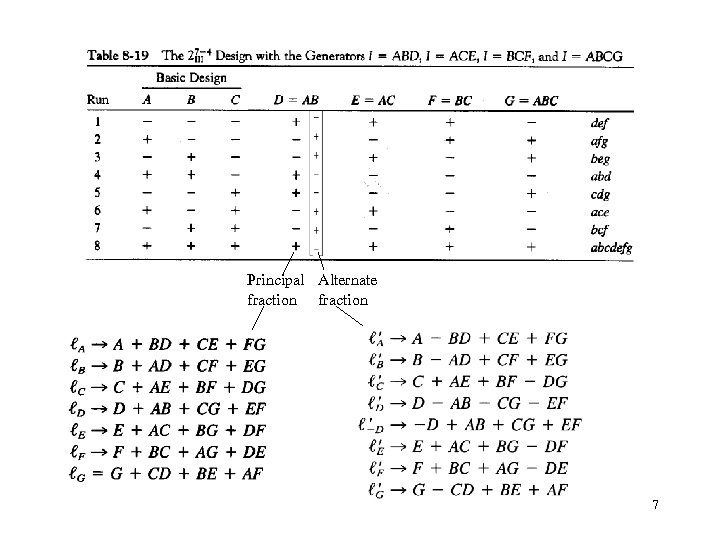Principal Alternate fraction 7

Effects from the combined design • Be careful – these rules only work for Resolution III designs • There are other rules for Resolution IV designs, and other methods for adding runs to fractions to de-alias effects of interest 8

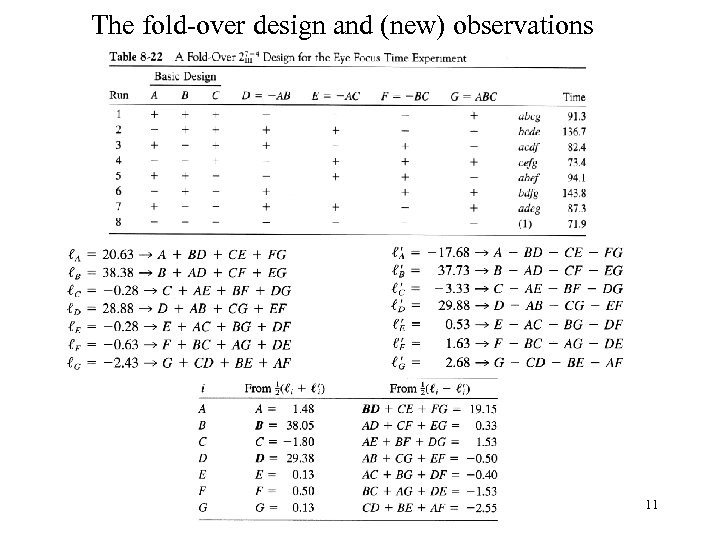
Resolution III Designs – Example 8 -7 • Response: eye focus time • Seven factors, two levels each, a design • First screening, then concentrate on important factors 9

• l. A, l. B, and l. D are large, but the interpretation of the data is not unique • As ABD is a word in the defining relation, this design projects into a replicated design • As the projected design is a resolution three design, A is aliased with BD, and so on • A second fraction is needed (with all the signs reversed) to separate the main effects with the 2 fis. 10

The fold-over design and (new) observations 11

Plackett-Burman Designs • These are a different class of 2 -level, resolution III design • k = N-1 variables, N runs • The number of runs, N, needs only be a multiple of four N = 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, … • The designs where N = 12, 20, 24, etc. are called nongeometric PB designs • PB designs have a messy alias structure – be careful 12

• Generating a nongeometric PB design matrix 13

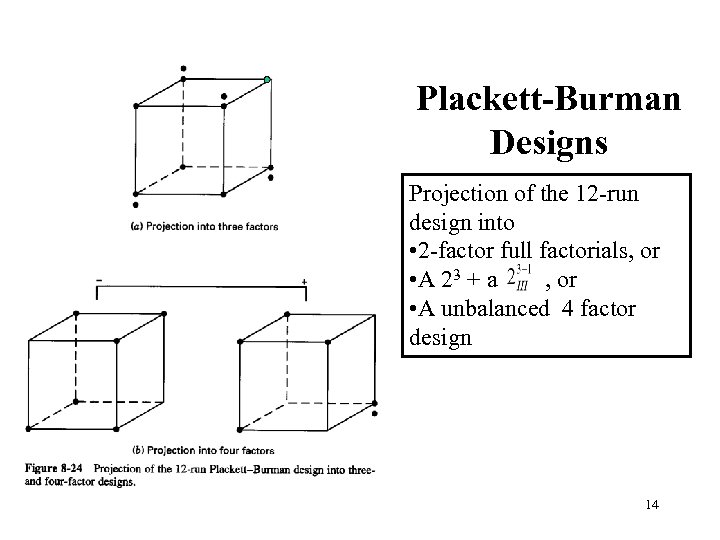Plackett-Burman Designs Projection of the 12 -run design into • 2 -factor full factorials, or • A 2 3 + a , or • A unbalanced 4 factor design 14

Plackett-Burman Designs • The alias structure is complex in the PB designs • For example, with N = 12 and k = 11, every main effect is aliased with every 2 FI not involving itself • Every 2 FI alias chain has 45 terms • Partial aliasing can greatly complicate interpretation • Interactions can be particularly disruptive • Use very, very carefully (maybe never) 15

Resolution IV Designs: Section 8 -6 • Designs with main effects not aliased with twofactor interactions, and some 2 fis are aliased with each other • Any design must contain at least 2 k runs • + its reflection (fold over) 16

Resolution IV and V Designs • Aliased two-factor interactions can be separated by folding over resolution IV designs • Break the 2 fis involving a specific factor • Break the 2 fis on a specific alias chain • Break as many 2 fi interaction alias chains as possible • One method is to run a second fraction in which the sign is reversed on every design generator that has an even number of letters • Folding over a resolution IV designs will not necessarily separate all 2 fis 17

Resolution IV and V Designs • In resolution V designs main effects and 2 fis do not alias with other main effects and 2 fis – powerful • Standard resolution V designs require large number of runs => irregular resolution V fractional factorials • A complete fold over of a resolution IV or V design is usually unnecessary, as adding small number of runs to the original fraction (partial fold over) can de-alias the few aliased interactions of interest 18

Partial fold over (semifold) • An alternative to a complete fold over • For a design , only 8 runs (as opposed to 16 runs as in a complete fold over) are needed • Procedure: o Construct a single-factor fold over in the usual way by changing the signs on a factor involved in a 2 -fi of interest o Select only half of the fold-over runs by choosing those runs where the chosen factor is either at its high or low level. Select the level that you believe will generate the most desirable response 19

Partial fold over (semifold) • For a design , the combined design has 16 (original fraction) + 16/2 (partial fold over) = 24 runs • Defining relation and aliasing relations for the combined (original fraction + partial fold over) are the same as those for the combined (original fraction + complete fold over) 20

General Method for Finding Aliasing Relations • • For a 2 k-p fractional factorial design: use the complete defining relation For more complex settings, e. g. , irregular fractions and partial fold-over designs: use a general method • Procedure: 1. Make a polynomial or regression model in the form y = X 1 b 1 + e y is an n × 1 vector of the responses, X 1 is an n × p 1 matrix containing the design matrix expanded to the form of the model that the experimenter is fitting, β 1 is an p 1 × 1 vector of the model parameters, and ε is an n × 1 vector of errors. o The least squares estimate of β 1 is 21

• Procedure: 3. Adding another term to the model y = X 1 b 1 + X 2 b 2+ e where X 2 is an n × p 2 matrix containing additional variables that are not in the fitted model and β 2 is a p 2× 1 vector of the parameters associated with these variables. 4. It can be easily shown that where is called the alias matrix. The elements of this matrix operating on β 2 identify the alias relationships for the parameters in the vector β 1. 22

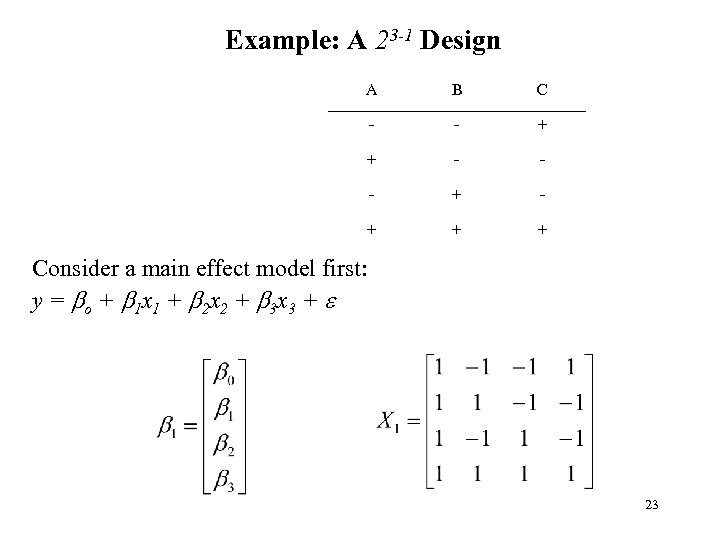Example: A 23 -1 Design A B C _ _ + + _ _ _ + + + Consider a main effect model first: y = bo + b 1 x 1 + b 2 x 2 + b 3 x 3 + e 23

In order to consider the aliasing relations between main and two factor interactions, add corresponding terms to the model: y = bo + b 1 x 1 + b 2 x 2 + b 3 x 3 + b 12 x 1 x 2 + b 13 x 1 x 3 + b 23 x 2 x 3 + e 24

25