Residential Workshop Template Slide-Show The sequence of slides

Residential Workshop* Template Slide-Show *The sequence of slides may vary during either Workshops or Masterclass from Patrick Mc. Nutt FRSA Additional materials can be located under e. Learning & Games Academy at www. patrickmcnutt. com

Economic Foundations (also go direct to Slide No 17) *from Topics 1 & 2 Market System: Technology and e. Needs *from Topics 3 & 4 Rational Behaviour The Bayesian persuasion problem

What is game theory about? Visit www. patrickmcnutt. com • • • Observed behaviour (inductive) in a game, G. Identify the players in the game and the player’s type. Finding the patterns in rival behaviour. Game => information on opponent type, recognised interdependence, actionreaction, belief systems. Payoff depends on what each player believes about the other. . Updating belief systems. What is a player’s true payoff? Independence v interdependence; one-shot v repeated play. • Consumers’ preferences as technology in a game.

Failure of Law of One Price Hypothesis: BIN Price < END price Are ‘onsumers’ irrational? Latent transaction costs Credible threats & belief systems

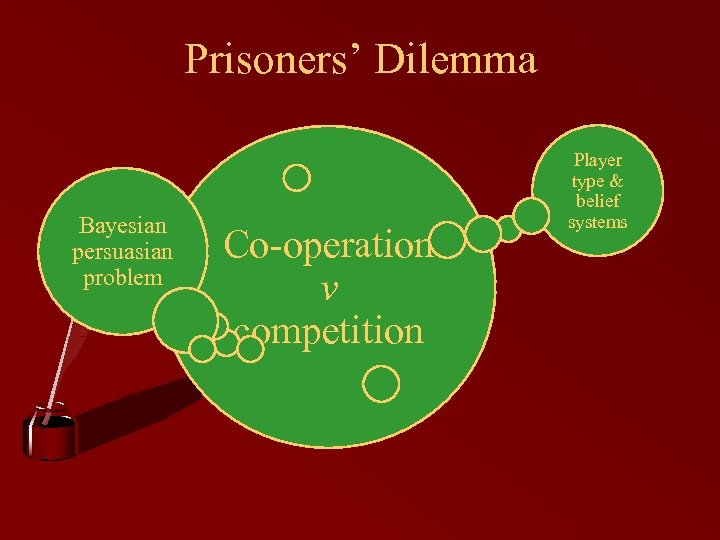Prisoners’ Dilemma Bayesian persuasian problem Co-operation v competition Player type & belief systems

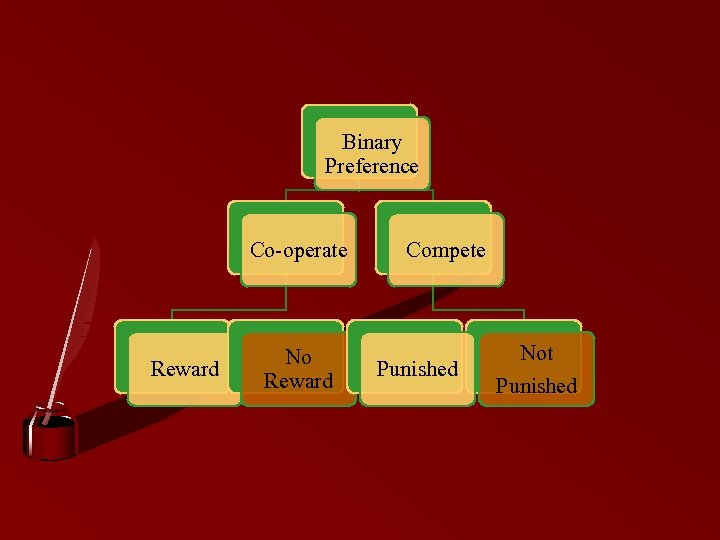Binary Preference Co-operate Reward No Reward Compete Punished Not Punished

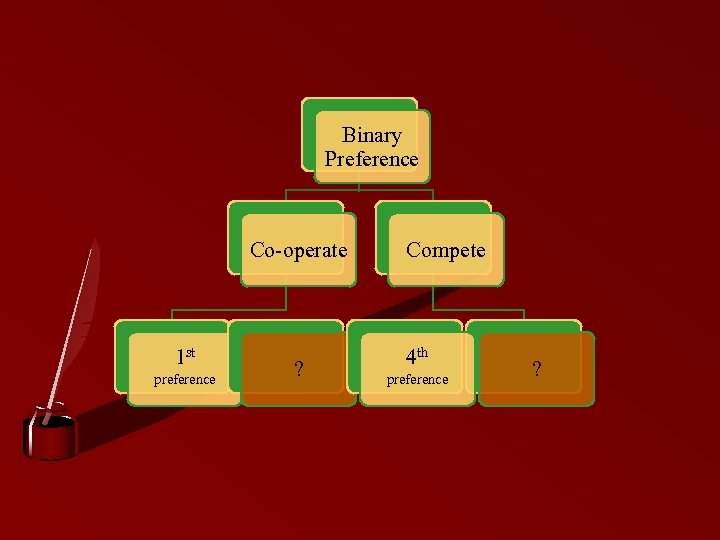Binary Preference Co-operate 1 st preference ? Compete 4 th preference ?

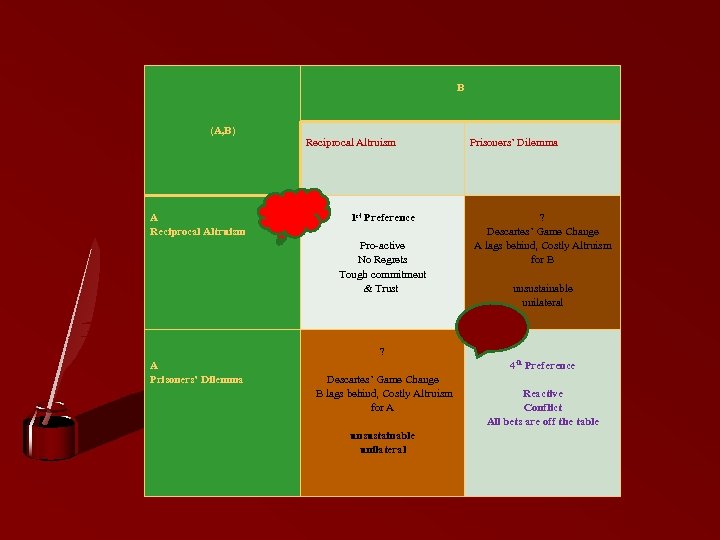(A, B) A Reciprocal Altruism B Reciprocal Altruism Prisoners’ Dilemma 1 st Preference Pro-active No Regrets Tough commitment & Trust ? A Prisoners’ Dilemma ? Descartes’ Game Change A lags behind, Costly Altruism for B unsustainable unilateral 4 th Preference Descartes’ Game Change B lags behind, Costly Altruism for A unsustainable unilateral Reactive Conflict All bets are off the table

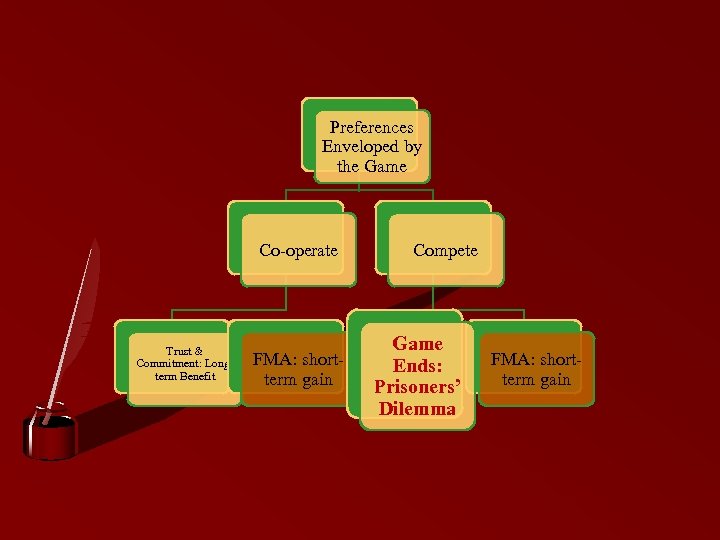Preferences Enveloped by the Game Co-operate Trust & Commitment: Longterm Benefit FMA: shortterm gain Compete Game Ends: Prisoners’ Dilemma FMA: shortterm gain

Payoffs reflect preference order. Guaranteed a 2 but there is an elusive 3 What if? Strategy I: cooperate What if? Strategy II: compete. Then if Strategy I is the consensus……. . ? Strategy II Strategy I 2, 2 0, 3 Strategy II 3, 0 1, 1 Nash Equilibrium

Topics 1 & 2 to Topics 3 & 4 Framework T/3 Capacity and Credible Threat Camouflage Commitment

Example A: What is type? If you believe it to be true that Leo the Liar will never tell the truth, how do you respond to his helping hand as you cling for your life over the precipice of a cliff? Do you ignore his helping? Do you rely instead on the many apps on your smartphone, so tightly grasped in your other hand, trying to make contact with your best friend to come and rescue you? Define Strategy Cooperation arises in this instance if you and Leo as players in a game can infer from past behaviour that both of you are likely to be trustworthy. Leo may forgo the short term gain of keeping to type for the long term benefit of your friendship. He rescues you from the cliff. You, however, will use the experience in order to determine whether or not to believe Leo in the future.

Example B: Player’s belief system Your company’s strategy is s 1: delayed launch of a new innovative product for 2 years. Rumors do appear of an impending launch date. You do not deny such rumors. In the interim, an article appears a reputable trade journal reporting that a not dissimilar product is about to be launched by your competitor in the next few weeks. Define Strategy Do you stop and think about s 1? Do you reshape your strategy to s 2: launch the product as soon as possible?

Player type and signalling • Decisions are interpreted as signals • Observed patterns and Critical Time Line (CTLs). Go to Appendix in Mc. Nutt • Recognition of market interdependence (zero-sum and entropy) • Price as a signal v Baumol model of TR max • Scale and size: cost leadership • Dividends as signals in a Marris model

Thinking Strategically… http: //www. managementinnovation. net/wpcontent/uploads/2011/08/Playing-War-Games-To-Win. pdf Principles of competition and cooperation. Chess and perfect information Backward induction and forward reasoning Timing in games Normal form and Extensive form

Player Types I Baumol type: player in a Bertrand game who will reduce price if demand is elastic. CL type: in Cournot capacity game we have a cost-leader type, CL, with reserve capacity. Incumbent and entrant: In the geography the incumbent already exists in the geography and the entrant is intent on entering or presents a threat of entry (contestable market). Dominant incumbent is a player with at least 40% of the market share. Often linked with Stackelberg or ‘top-dog’ in Besanko.

Economic Foundations Classroom Discussion on Elasticity and on Capacity http: //www. patrickmcnutt. com/elearning/kaelo-learning-interactions-2/ • Consumer preferences & demand • Elastic & Inelastic Demand DEMAND • Baumol’s TR Test & Operating Leverage SUPPLY • Capacity as a Credible Threat • Productivity: Wages Imperfectly Measured • Strategic Pricing STRATEGY • Pizza Paradox

The competitive threat! • Traditional Analysis is focused on answering this question for Company X: what market are we in and how can we do better? • Economics of strategy (T/3) asks: what market should we be in?

Perfect market: perfect competition • Defining a perfect market as follows: If ΔPi increases, then the firm’s output = 0 or rivals follow the price increase. • In a perfect market price differences cannot persist across time • Perfect competition = perfect market + near rivals So perfect market ≠> perfect competition but perfect competition => perfect market

Reasons to Play • Law of One Price • Relevance of supply and demand: Say’s law for 21 st century Reason 1 • Elasticity & rival reaction as price discipline • Individual behaviour; Heisenberg uncertainty principle • Individuals are not like ‘white mice in an experiment’ Reason 2 • Nudge behaviour • Uncertainty about value • Wages [price] and productivity[value] divergence: noise Reason 3 • Capacity constraints

Costs of not being a Player • No playbook • Bounded rationality and opportunity costs with trade-offs • Make or Buy dilemma • First Mover Advantage (FMA) v Second Mover Advantage (SMA) or Play to win v Play not to lose! • Fail to anticipate competitor reactions • Follower status ‘behind the curve’ • Technology lag and failure to differentiate ‘fast enough’ to sustain a competitive advantage • Near rival will try to minimise your gains by playing a minimax strategy

Non Co-operative Strategic Games Step 1 • Player type and T/3 and value net • Game Dimension: geography or product category Step 2 • Elasticity & Unilateral Price Reaction • Zero-Sum Constraints Step 3 • Reserve Capacity & Credible Threat • Camouflage & Commitment

Oligopoly, Games & T/3 Framework • • Study of strategic interactions: how firms adopt alternative strategies by taking into account rival behaviour Structured and logical method of considering strategic situations. It makes possible breaking down a competitive situation into its key elements and analysing the dynamics between the players. • Key elements: • Players. Company or manager. • Strategies. • Payoffs • Equilibrium. Every player plays her best strategy given the strategies of the other players. Objective. To explore oligopolistic industries from a game embedded strategy (GEMS) perspective. The use of T/3 framework, which considers 3 key dimensions (Type, Technology & Time), will allow players to better predict the likely strategic response of competitors when analysing rival competition. • •

Decoding Strategy & Pattern Sequencing Complete knowledge on the type and complete information of the identity of a near rival: Actionyou -> Reactionnear-rival ->…. . -> Reactions……Nash. Replyyou…. . Strategy defined in terms of an equilibrium: how well either player does in a game depends on what each player believes the other player will do.

Surprise and Noise • Binary reaction: • Will Player B react? Yes or No? • If YES, decision may be parked as ‘do-nothing strategy’ • If NO, decision proceeds on error • Surprise, bias and noise • Non-binary reaction: Player B will react. Probability = x% • Probability (1 -x)% ANOther player will react? • Decision taking on conjecture of likely reaction • No Surprise with Contingent risk profile

Player Types II Extant incumbent: An incumbent that has survived a negative event such as a price war of a failed innovation or technology-lag. De novo entrant: An entrant intent on entering – the incumbents can observe plant building or product launch. Potential entrant: An entrant that presents a threat of entry into a game through signalling with noise or ‘moonshot’ or planned capacity building in another game [with economies of scope). Stackelberg type: A price leader in a Bertrand game moving first in the belief that others will follow or in the knowledge that other are disciplined (often linked to collusive behaviour).

Two basic forms of model are used to analyse games: The Normal (Strategic) Form of a game • Summarises players, strategies and payoffs in a ‘payoff matrix’ • Particularly suitable for analysing static games (e. g. games with simultaneous moves). Making choices simultaneously The Extensive Form of a game • Summarises players, strategies and payoffs in a ‘game tree’ • Useful where the timing of players actions, and the information they will have when they must take these actions, is important (e. g. games with sequential moves)

Strategy & Games Stage 1 • Normal strategic form & Extensive form games • Imperfect information on game dimension (enveloped) • Incomplete information on player type & payoffs Stage 2 • Dominant Strategy • Prisoners’ Dilemma • Limit Entry Games Stage 3 • Nash Equilibrium & Payoff Dominant • Kantian Altruistic Equilibrium • Evolutionary Stable Strategy (Robins in the Garden)

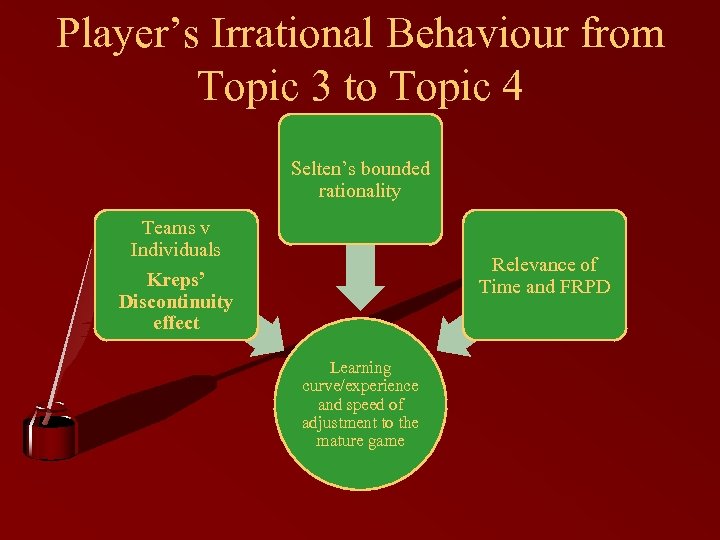Player’s Irrational Behaviour from Topic 3 to Topic 4 Selten’s bounded rationality Teams v Individuals Relevance of Time and FRPD Kreps’ Discontinuity effect Learning curve/experience and speed of adjustment to the mature game

Failure of Law of One Price BIN Price < END price Game Dimension Sufficiently Intelligent Algorithm v Rational ‘onsumer’

Game Strategy • Nash premise: Action, Reaction and CV matrix • Non-cooperative sequential (dynamic) games • TR Test Mc. Nutt pp 48. . one-shot move • Limit price [to avoid entry] and predatory pricing to force exit. • Near rival plays Minimax, so I play Maximin [focus on my worst minimum payoff and try to maximise]. • Segmentation strategy to obtain FMA • Relevance of ‘chain-store’ tumbling price paradox • Dark Strategy and 3 Mistakes in Mc. Nutt pp 117 -118

Nash Equilibrium • Many common games (and therefore many common strategic situations) are not solvable. Is behaviour irrational? • Search for a solution in Nash equilibrium • Nash Equilibrium, is now one of the most fundamental concepts in the economics of strategy

In order for the NE of a game to be a compelling solution assumes: Players are rational The rules of the game are common knowledge Common knowledge of players’ rationality A source of ‘Common Beliefs’ • Focal Points • Pre-game communication • Learning • Convention

Describe (prices as signals) game dimension • Players and type of players • Prices interpreted as signals • Understand (price) elasticity of demand cross-price elasticity • Patterns of observed behaviour • Leader-follower as knowledge • Accommodation v entry deterrence • Reaction, signalling and Nash equilibrium: ‘best you can do, given reaction of competitor’

Player A’s Conjectural Variation [CV] Matrix In a what-if scenario, a player creates a CV matrix to allow (i) filtering of the competitors (ii) that are likely to react to each action. Player A Competitor B Competitor C Competitor D Near Rival Action 1 Lower price CV ≠ 0 CV = 0 B Action 2 Launch new product CV ≠ 0 CV = 0 B or C Action 3 New innovation CV = 0 CV ≠ 0 D Action 4…… Probability

Normal Game Dimension • Simultaneous games • Normal form game dimension with payoff matrices, wherein payoffs reflect preference order. • Player type and camouflage • Dominant strategy, Prisoners’ dilemma, Nash equilibrium.

Extensive Game Dimension • Constructing an action-reaction sequence of moves in search for a pattern. • Non-cooperative sequential (dynamic) games • Extensive form game dimension with decision tree and backward induction • Credible Threats • Commitment strategies • Signaling and Belief Systems

Entry Deterrent Strategy & Barriers to entry • Reputation of the incumbents • Capacity building • Entry function of the entrant • De novo and entry at time period t • Potential entrant - forces reaction at time period t from incumbent • Coogan’s bluff strategy (classic poker strategy) and enter the game.

Limit Pricing Model Besanko pp 207 -211 and Mc. Nutt pp 85 -88 • Outline the game dimension: dominant incumbents v camouflaged entrant type • Define strategy set for incumbents: commitment and punishment • Allow entry and define the equilibrium • Extensive form preference - entry deterrent strategy v accommodation [next slides]

Extensive Form Games • The Extensive Form is particularly useful for analysing games in which players make choices sequentially • The structure of the game is represented by a game tree. Play begins at the initial node and proceeds according to the structure of the tree and the choices that players make

Extensive Form Games we will only consider games involving two players we will only consider games in which players can observe the moves made by players earlier on in the game (these are called games of complete information) we will allow for ‘fooling behaviour’ and camouflage by an entrant

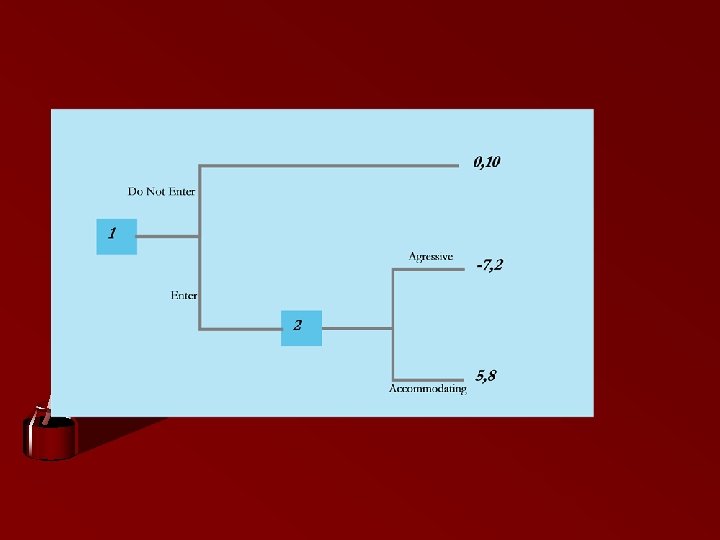
Online Lecture Exercise Strategy Profile - Fid the Nash Trap Observations and Intelligence In the decision tree narrative there is no other firm to compete with in this game – it is the incumbent v entrant. But if the entrant does not enter, fight and accommodate yield the same payoffs to both players Hypothesis 1 If the entrant does not enter, it does not matter what the incumbent chooses to do. Hypothesis 2 The incumbent will not lower prices if the entrant does not enter.

CLASS EXERCISE QUESTIONS A. Convert the decision tree into a normal form payoff matrix. B. Find the Nash equilibria C. Repeat A and B on the credible threat of entry from a spherical competitor [check pp 173 -175 in Mc. Nutt Decoding Strategy] D. Results in A+B+C written up as an Aide Memoire for management. E. Strategy Profile = Aide Memoire

Nash Equilibrium & Define a price war • Construct the Bertrand reaction functions • Compute a Critical Time Line (CTL)from observed signals. . • Find a price point of intersection • Case Analysis of Sony v Microsoft in Mc. Nutt pp 141 -144 and also in Kaelo v 2. 0

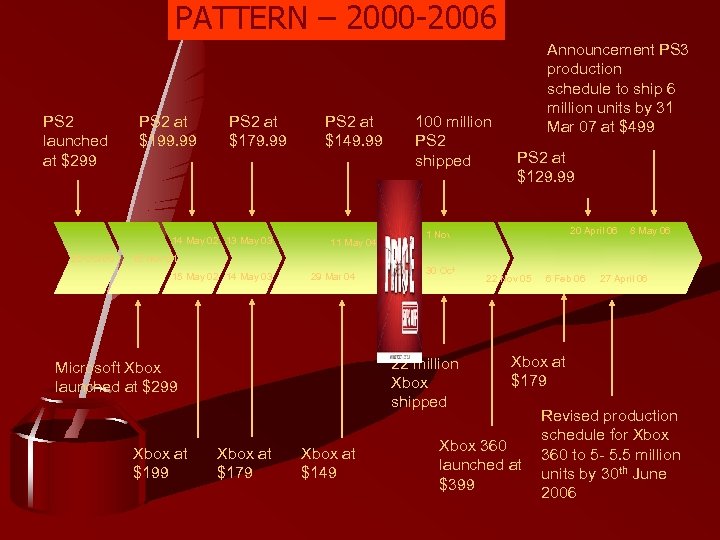PATTERN – 2000 -2006 PS 2 launched at $299 PS 2 at $199. 99 PS 2 at $179. 99 14 May 02 13 May 03 26 Oct 00 PS 2 at $149. 99 11 May 04 100 million PS 2 shipped Announcement PS 3 production schedule to ship 6 million units by 31 Mar 07 at $499 PS 2 at $129. 99 20 April 06 1 Nov 05 8 May 06 15 Nov 01 15 May 02 14 May 03 29 Mar 04 22 million Xbox shipped Microsoft Xbox launched at $299 Xbox at $199 30 Oct 05 Xbox at $179 Xbox at $149 22 Nov 05 6 Feb 06 27 April 06 Xbox at $179 Xbox 360 launched at $399 Revised production schedule for Xbox 360 to 5 - 5. 5 million units by 30 th June 2006

Classroom Exercise on Nash Reply Practical III on Price Data Trends: Compute the NE and represent the equilibrium in a Nash. Bertrand Reply Function

Dominant Strategy Equilibrium Iterative Deletion of Dominated Strategies Nash Equilibrium Dominant Strategies • A player has a (strictly) dominant strategy if, for each possible action that his opponent can take, that strategy leads to a payoff that is strictly greater than the payoff associated with any of his other strategies • A player can have no more than one dominant strategy and in many games, will have none

The ‘signalling’ payoffs & assurance • A & B have common interest in coordinating strategies. Player A never choose ‘Bottom’ if rational, only ‘Top’, and Player B should play weakly dominant ‘Left’. B Left A Right Top 3, 3 1, 2 Bottom 2, 0 0, 0 • Problem of coordination where players have different preferences but common interest in coordinating strategies. • Classroom discussion on Folk Theorem • Next slide for Assurance Game on coordination and trust: Payoff-dominant v risk-dominant play.

Alliance No Alliance/No JV Alliance/JV 2, 2 Payoff-dominant 0, 1 No Alliance/No JV 1, 0 1, 1 Risk-dominant

Five Games of Strategic Interaction Pure Conflict The Prisoner’s Dilemma Chicken games The Battle of the Sexes Coordination Game with Asymmetric Information: Sony v Toshiba

Play Games of Strategic Interaction Conflict & The Prisoner’s Dilemma Trust & Commitment Play a Game http: //ncase. me/trust/

Toshiba Blu-Ray Toshiba HD-DVD Sony Blu-Ray 10, 1 0, 0 Sony HD-DVD 0, 0 1, 4

Minimax criteria. If you look at examples in the book Decoding Strategy pp 148 -151 we discuss this next slides for Near-rival v Apple but it can be applied also in any market-as-agame Strategy Simply, identify the near rival [reacting first] and set up the game tree assuming that near-rival plays minimax, that is, confining you to the least of the greatest market shares in the game - so then you play maximin, to maximise the least loss.

n Player B S 4 Player A: S 1 S 2 S 3 Column maximum Minimax strategy by B S 5 S 6 S 7 5 70 35 95 60 30 50 55 30 40 90 10 95 70 55 90 Row Minimum Maximin strategy by A 5 55 10

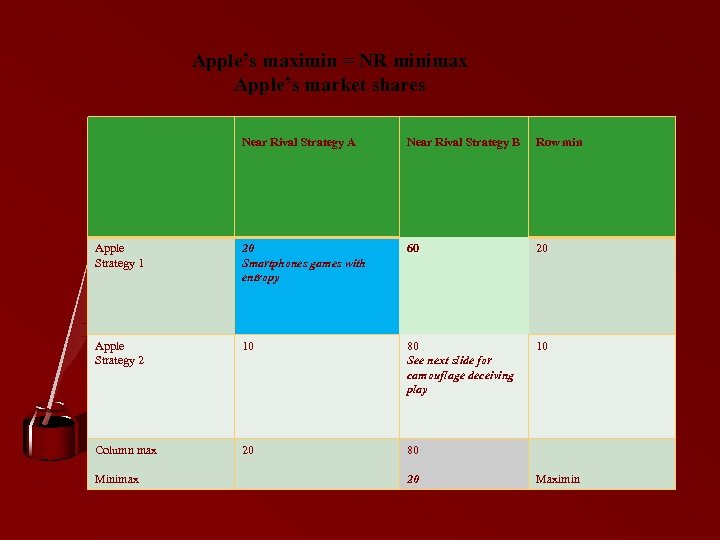Apple’s maximin = NR minimax Apple’s market shares Near Rival Strategy A Near Rival Strategy B Row min Apple Strategy 1 20 Smartphones games with entropy 60 20 Apple Strategy 2 10 80 See next slide for camouflage deceiving play 10 Column max 20 80 Minimax 20 Maximin

Apple’s ‘loading the dice’ strategy Apple’s market shares adapted from pp 152 in Mc. Nutt’s Decoding Strategy with camouflage, deceiving/fooling and mixed strategy Near Rival Strategy A Near Rival Strategy B Apple Strategy 1 20 Apple Strategy 2 80 60 i. Phone 7 in 2016 nano i. Phone 2018 10

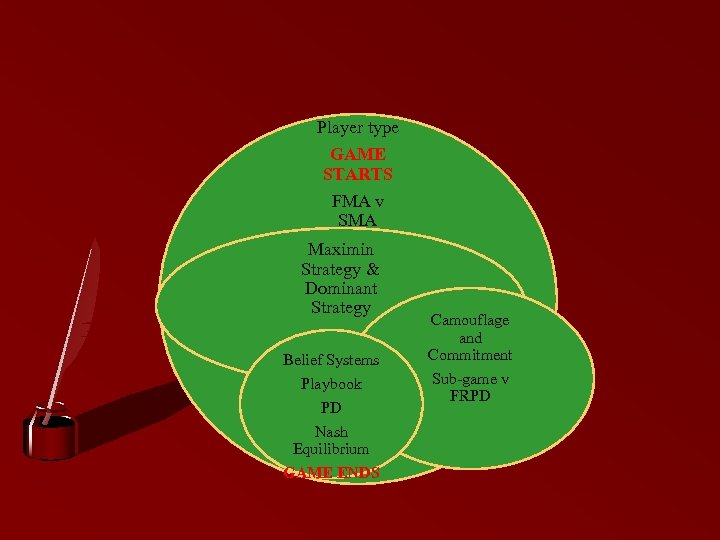Player type GAME STARTS FMA v SMA Maximin Strategy & Dominant Strategy Belief Systems Playbook PD Nash Equilibrium GAME ENDS Camouflage and Commitment Sub-game v FRPD

Post-Workshop http: //ncase. me/trust/ 1. Readings allocated from class 2. Online Lectures Prof. Prompts 3. Discussion Threads 4. Final Assessment Uploaded to BB