Решётка Браве Элементарные ячейки


Решётка Браве Элементарные ячейки Кристаллические структуры

Симметрия кристаллов Пространственной решеткой будем называть совокупность точек пространства, радиус-векторы которых имеют вид: R=n 1 a 1+n 2 a 2+n 3 a 3, где аi – тройка произвольных некомпланарных векторов, ni – принимают всевозможные целочисленные значения. Эти точки – узлы. Основное свойство кристаллической решетки – трансляционная инвариантность. Параллелепипед, построенный на a 1, a 2, a 3 – называется элементарной ячейкой данной пространственной решетки, а их модули – периодами идентичности или постоянными решетки. Идеальный кристалл – это пространственная решетка, с каждым узлом которой однозначно связан атом, молекула, группа атомов… Этот атом, молекула… - является базисом. Структура = решетка + базис

УСЛОВНАЯ РЕШЕТКА Cubic-face-centered
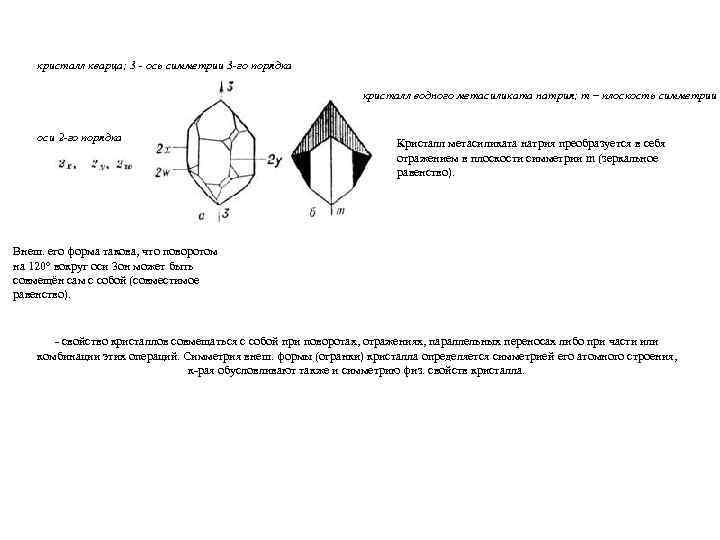
кристалл кварца; 3 - ось симметрии 3 -го порядка кристалл водного метасиликата натрия; m – плоскость симметрии оси 2 -го порядка Кристалл метасиликата натрия преобразуется в себя отражением в плоскости симметрии m (зеркальное равенство). Внеш. его форма такова, что поворотом на 120° вокруг оси 3 он может быть совмещён сам с собой (совместимое равенство). - свойство кристаллов совмещаться с собой при поворотах, отражениях, параллельных переносах либо при части или комбинации этих операций. Симметрия внеш. формы (огранки) кристалла определяется симметрией его атомного строения, к-рая обусловливают также и симметрию физ. свойств кристалла.
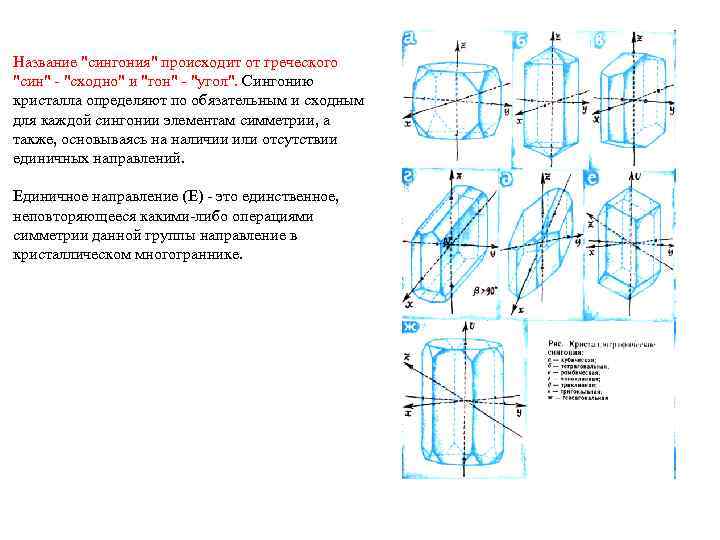
Название "сингония" происходит от греческого "син" - "сходно" и "гон" - "угол". Сингонию кристалла определяют по обязательным и сходным для каждой сингонии элементам симметрии, а также, основываясь на наличии или отсутствии единичных направлений. Единичное направление (Е) - это единственное, неповторяющееся какими-либо операциями симметрии данной группы направление в кристаллическом многограннике.
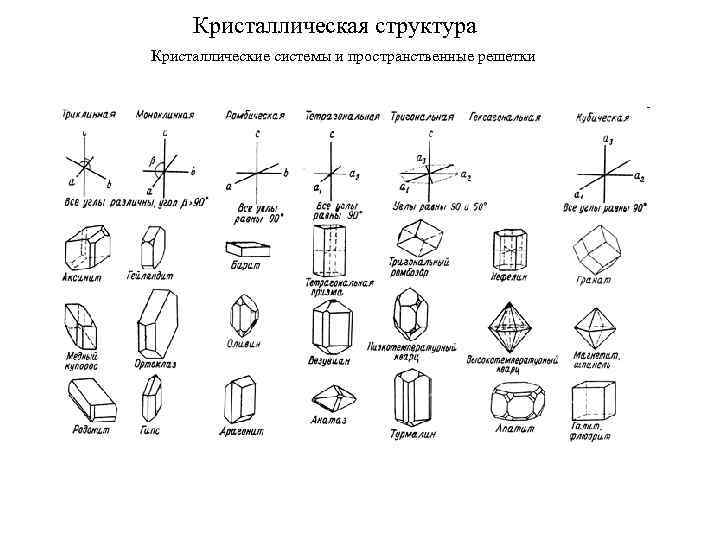
Кристаллическая структура Кристаллические системы и пространственные решетки

Резюме лекции 6 (Симметрия кристаллов) + повторяем Пространственная решетка = Решётка Браве примитивная Элементарные ячейки условная эл. яч. Кристаллическая структура = решетка + базис Координационное число, плотность упаковки Преобразование симметрии (точечные группы) Классификация решеток Браве (3 D).

Grundmann_physics of semiconductors- 2006

При точечной симметрии одна точка сохраняет своё положение. В трехмерном пространстве существует 32 вида центральной симметрии. В символах Шенфлиса они описываются следующим образом: • Сn, циклические группы — группы с единственным особым направлением, представленным поворотной осью симметрии, — обозначаются буквой С, с нижним цифровым индексом n, соответствующим порядку этой оси. • Сni — группы с единственной инверсионной осью симметрии сопровождаются нижним индексом i. • Cv (от нем. vertical — вертикальный) — для плоскостей, расположенных вдоль единственной или главной оси симметрии, которая всегда мыслится вертикальной. • Ch (от нем. horisontal — горизонтальный) — для плоскости, перпендикулярной к главной оси симметрии. • S (от нем. spiegel — зеркало) — для плоскости неопределенной ориентации, то есть не фиксированной ввиду отсутствия в группе иных элементов симметрии • O, T — группы симметрии с несколькими осями высшего порядка — группы кубической сингонии — обозначаются буквой О в случае, если они содержат полный набор осей симметрии, или буквой Т — если в группе отсутствуют диагональные оси симметрии. • Dn — является группой Сn с добавочной осью симметрии второго порядка, перпендикулярной исходной оси. • Dnh также имеет горизонтальную плоскость симметрии. • Dnv также имеет вертикальную плоскость симметрии; n может равняться 1, 2, 3, 4, 6.
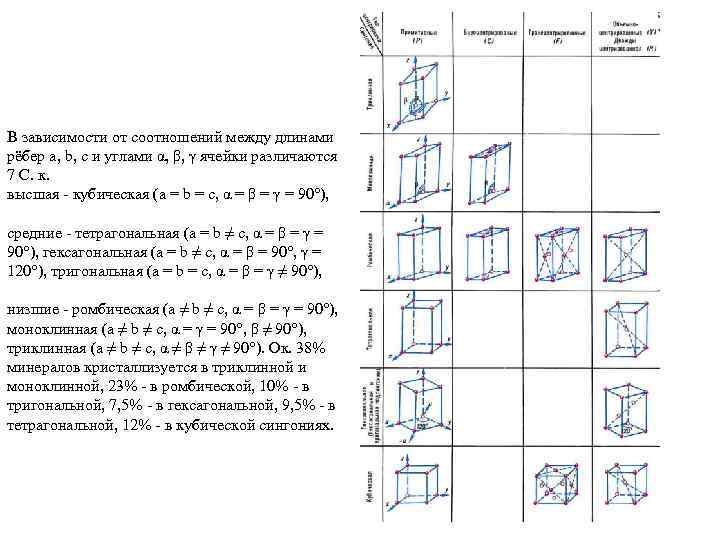
B зависимости от соотношений между длинами рёбер a, b, c и углами α, β, γ ячейки различаются 7 C. к. высшая - кубическая (a = b = c, α = β = γ = 90°), средние - тетрагональная (a = b ≠ c, α = β = γ = 90°), гексагональная (a = b ≠ c, α = β = 90°, γ = 120°), тригональная (a = b = c, α = β = γ ≠ 90°), низшие - ромбическая (a ≠ b ≠ c, α = β = γ = 90°), моноклинная (a ≠ b ≠ c, α = γ = 90°, β ≠ 90°), триклинная (a ≠ b ≠ c, α ≠ β ≠ γ ≠ 90°). Oк. 38% минералов кристаллизуется в триклинной и моноклинной, 23% - в ромбической, 10% - в тригональной, 7, 5% - в гексагональной, 9, 5% - в тетрагональной, 12% - в кубической сингониях.

2 -ое важное свойство кристаллической решетки – поворотная симметрия (ось симметрия и плоскость симметрии). Центр инверсии Плоскости симметрии Оси симметрии
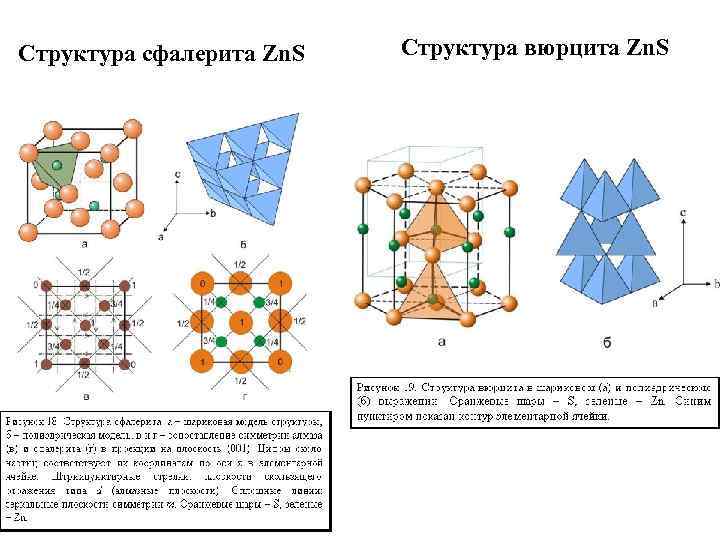
Структура сфалерита Zn. S Структура вюрцита Zn. S
лекция 6 идеальный кристалл.ppt
- Количество слайдов: 12

