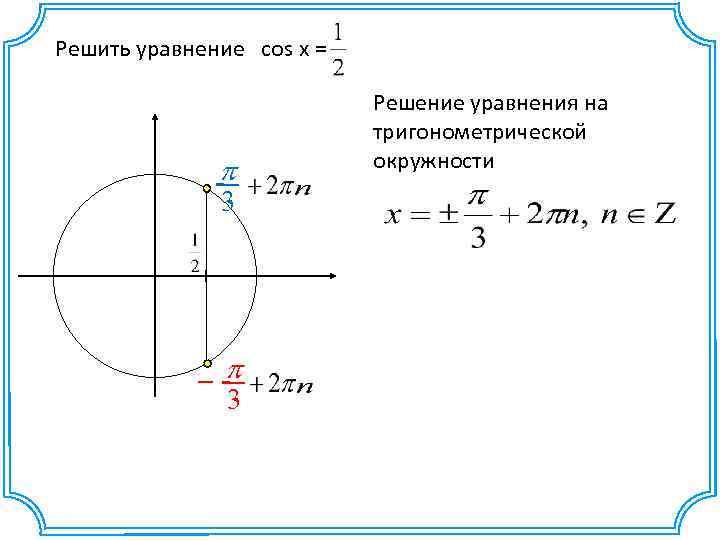
Решить уравнение cos x p 3 p

Решить уравнение cos x = p 3 –p 3 Решение уравнения на тригонометрической окружности

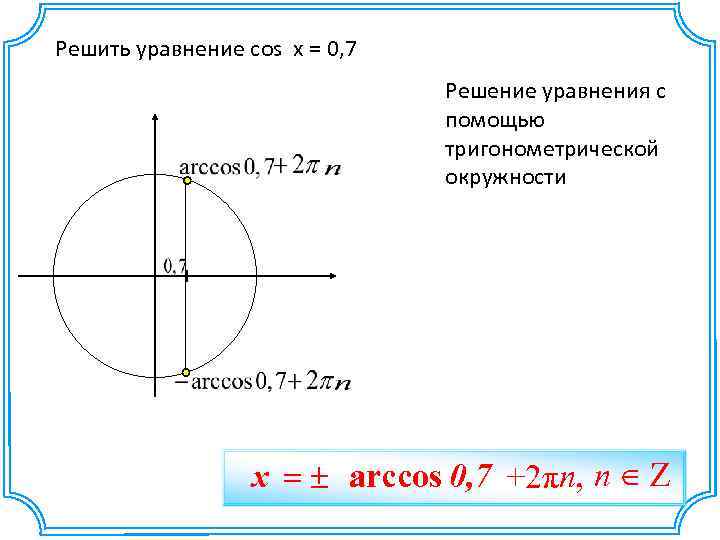Решить уравнение cos x = 0, 7 Решение уравнения с помощью тригонометрической окружности x = ± arccos 0, 7 +2πn, n Î Z

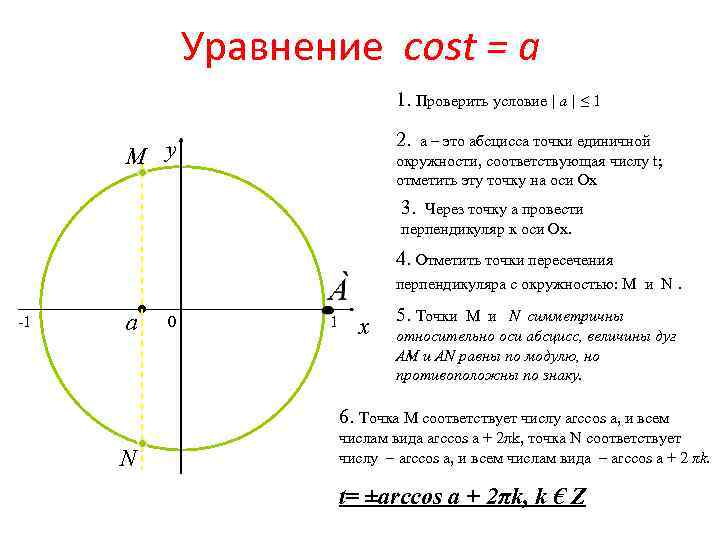Уравнение cost = a 1. Проверить условие | a | ≤ 1 2. a – это абсцисса точки единичной окружности, соответствующая числу t; отметить эту точку на оси Ох M y 3. Через точку а провести перпендикуляр к оси Ох. 4. Отметить точки пересечения перпендикуляра с окружностью: М и N. -1 a 0 1 x 5. Точки M и N симметричны относительно оси абсцисс, величины дуг AM и AN равны по модулю, но противоположны по знаку. 6. Точка M соответствует числу arccos a, и всем N числам вида arccos a + 2πk, точка N соответствует числу – arccos a, и всем числам вида – arccos а + 2 πk. t= ±arccos a + 2πk, k € Z

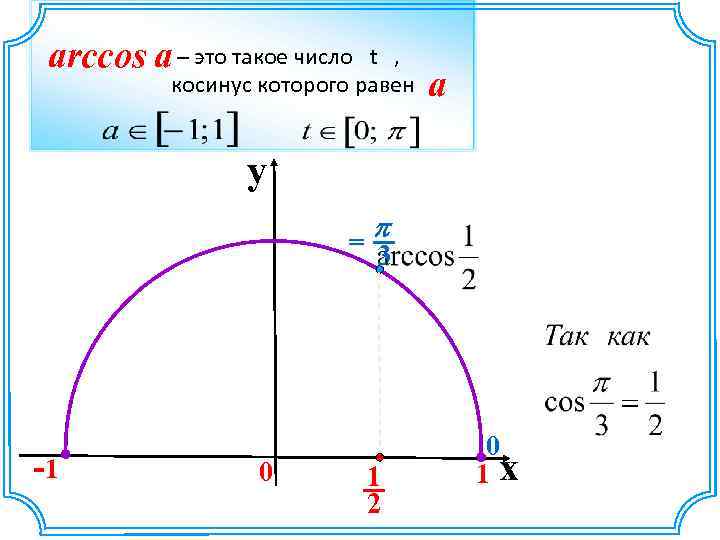arccos a – это такое число t , косинус которого равен a y p = 3 -1 0 1 2 0 1 x

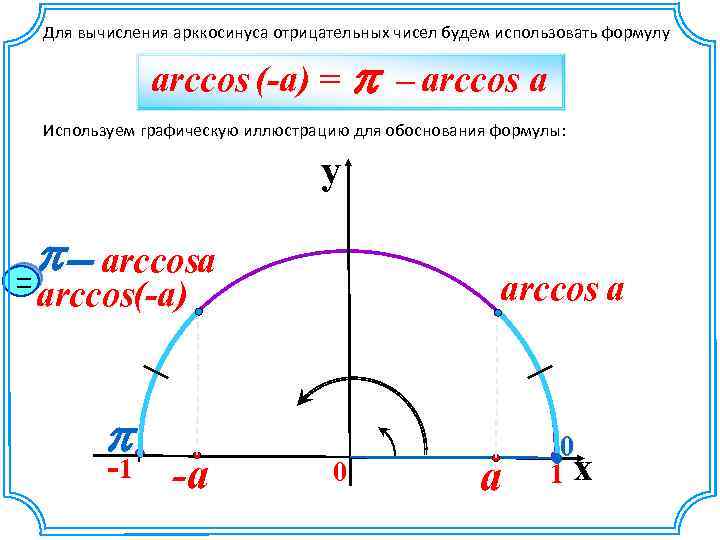Для вычисления арккосинуса отрицательных чисел будем использовать формулу arccos (-a) = p – arccos a Используем графическую иллюстрацию для обоснования формулы: y p- arccosa = arccos a arccos(-a) p -1 -a 0 1 x

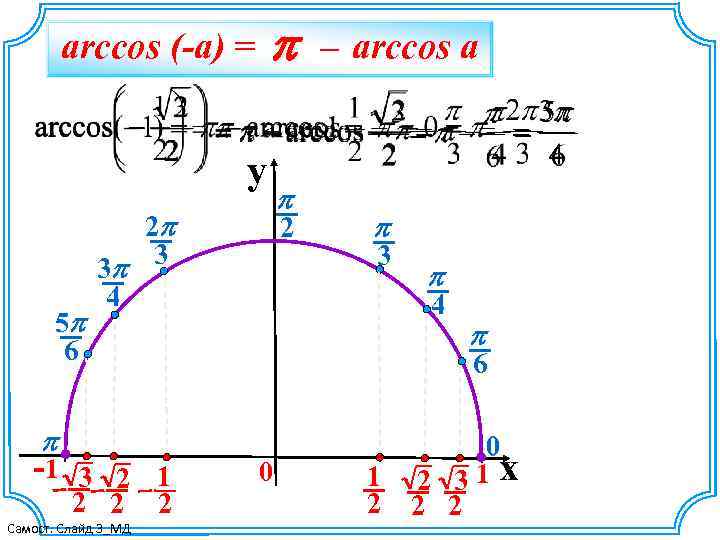p arccos (-a) = y 5 p 6 2 p 3 p 3 4 -1 3 2 1 Самост. Слайд 3_МД 2 p 3 p 4 p 6 p 2 2 p – arccos a 2 0 1 2 0 2 31 x 2 2

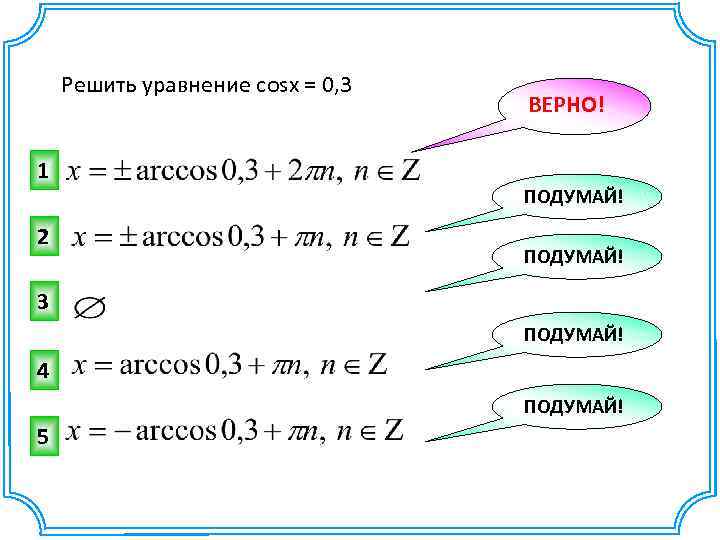Решить уравнение cosx = 0, 3 1 2 ВЕРНО! ПОДУМАЙ! 3 ПОДУМАЙ! 4 ПОДУМАЙ! 5

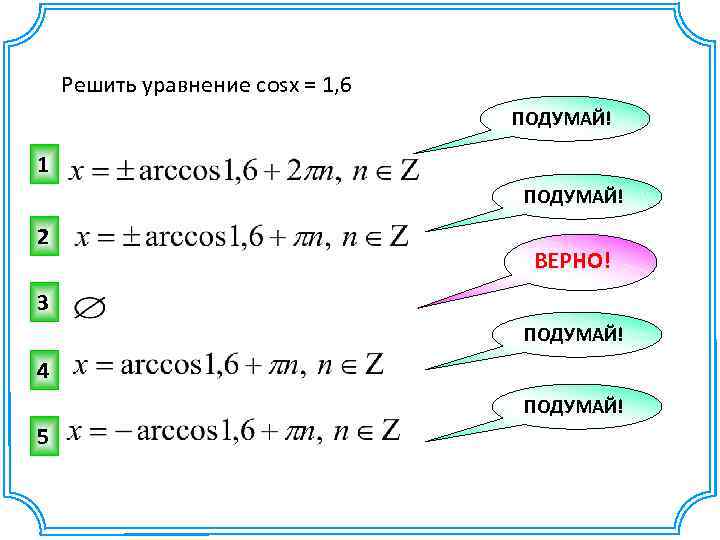Решить уравнение cosx = 1, 6 ПОДУМАЙ! 1 ПОДУМАЙ! 2 ВЕРНО! 3 ПОДУМАЙ! 4 ПОДУМАЙ! 5

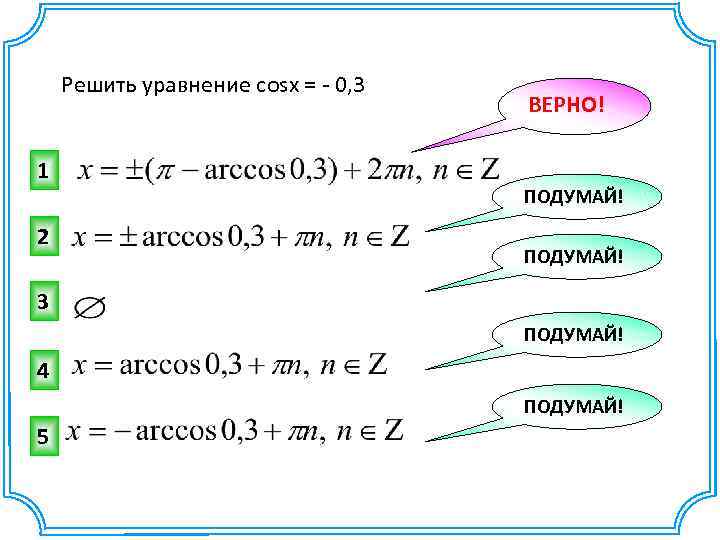Решить уравнение cosx = - 0, 3 1 2 ВЕРНО! ПОДУМАЙ! 3 ПОДУМАЙ! 4 ПОДУМАЙ! 5

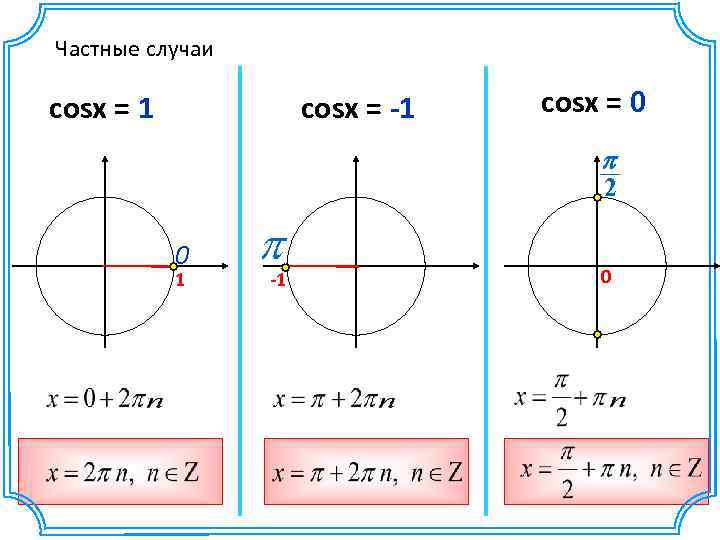Частные случаи cosx = 1 cosx = -1 cosx = 0 p 2 0 1 p -1 0