РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ МЕТОДА БРАУНА - РОБИНСОНА
Пусть первый игрок - это << Конкурент >>, а второй - << Фирма >>. Стратегии игрока 1 расположены по строкам, а игрока 2 - по столбцам матрицы выигрышей. Рассмотрим алгоритм фиктивного разыгрывания на примере игры этих двух игроков (1 - << Конкурент >>, 2 - << Фирма >>) с нулевой суммой с функцией игры , - наборы стратегий игроков (1 - << Конкурент >>, 2 - << Фирма >>) с нулевой суммой с функцией игры
Введем следующие обозначения: n - количество товаров, рассматриваемых в ассортиментной политике; k- номер комплексного показателя , k=1, 2, 3; i - номер критерия , i=1. . . Ik ;
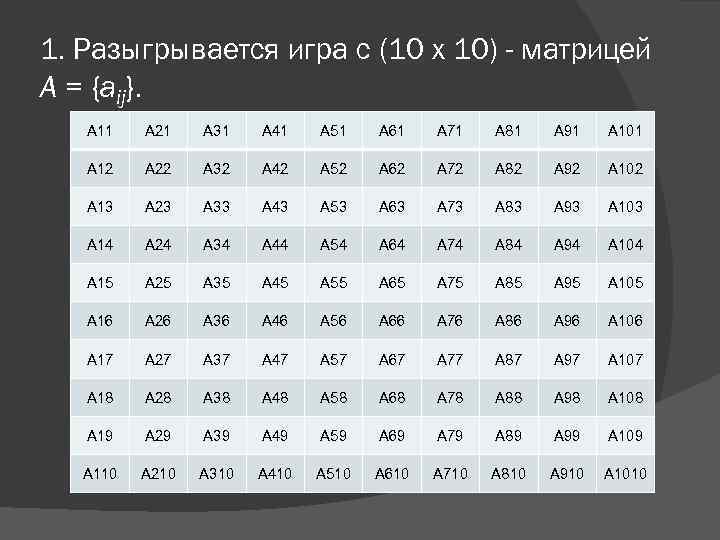
1. Разыгрывается игра с (10 x 10) - матрицей A = {aij}. A 11 A 21 A 31 A 41 A 51 A 61 A 71 A 81 A 91 A 101 A 12 A 22 A 32 A 42 A 52 A 62 A 72 A 82 A 92 A 102 A 13 A 23 A 33 A 43 A 53 A 63 A 73 A 83 A 93 A 103 A 14 A 24 A 34 A 44 A 54 A 64 A 74 A 84 A 94 A 104 A 15 A 25 A 35 A 45 A 55 A 65 A 75 A 85 A 95 A 105 A 16 A 26 A 36 A 46 A 56 A 66 A 76 A 86 A 96 A 106 A 17 A 27 A 37 A 47 A 57 A 67 A 77 A 87 A 97 A 107 A 18 A 28 A 38 A 48 A 58 A 68 A 78 A 88 A 98 A 108 A 19 A 29 A 39 A 49 A 59 A 69 A 79 A 89 A 99 A 109 A 110 A 210 A 310 A 410 A 510 A 610 A 710 A 810 A 910 A 1010
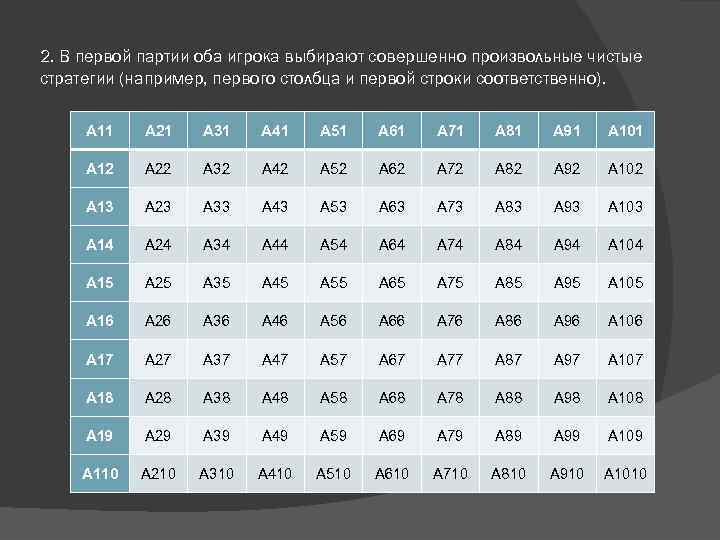
2. В первой партии оба игрока выбирают совершенно произвольные чистые стратегии (например, первого столбца и первой строки соответственно). A 11 A 21 A 31 A 41 A 51 A 61 A 71 A 81 A 91 A 101 A 12 A 22 A 32 A 42 A 52 A 62 A 72 A 82 A 92 A 102 A 13 A 23 A 33 A 43 A 53 A 63 A 73 A 83 A 93 A 103 A 14 A 24 A 34 A 44 A 54 A 64 A 74 A 84 A 94 A 104 A 15 A 25 A 35 A 45 A 55 A 65 A 75 A 85 A 95 A 105 A 16 A 26 A 36 A 46 A 56 A 66 A 76 A 86 A 96 A 106 A 17 A 27 A 37 A 47 A 57 A 67 A 77 A 87 A 97 A 107 A 18 A 28 A 38 A 48 A 58 A 68 A 78 A 88 A 98 A 108 A 19 A 29 A 39 A 49 A 59 A 69 A 79 A 89 A 99 A 109 A 110 A 210 A 310 A 410 A 510 A 610 A 710 A 810 A 910 A 1010
3. Игрок 1 выбирает такую чистую стратегию i из набора своих 10 стратегий x, которая максимизирует его средний выигрыш , при условии, что игрок 2 использует свою смешанную стртегию yk. 4. Игрок 2 выбирает такую чистую стратегию j из набора своих 10 стратегий y, которая минимизирует его средний проигрыш , при условии, что игрок 1 использует свою смешанную стртегию xk. Итак, предположим, что за первые k разыгрываний игрок 1 использовал i- ю стратегию раз , а игрок 2 - j-ю стратегию раз Тогда в (k+1)-й стратегии игрок 1 будет использовать ik + 1 -ю стратегию , а 2 - свою jk + 1 - ю стратегию.
Применение Результат решения - распределения вероятностей чистых стратегий игроков, т. е. распределения вероятностей товаров- стратегий для двух фирм << Фирмы >> и << Конкурента >>. Полученные вероятности можно интерпретировать так: если рекомендовано << Фирме >> крем для лица выпускать с вероятностью 0, 17 , это означает , что из 100 единиц выпускаемой продукции 17 единиц должны быть выпущены в виде крема для лица. Таким образом, если << Фирма >> будет придерживаться yk данного набора товарных групп в полученном соотношении для выпуска своей продукции, то это обеспечит ей успешную работу на рынке данных товаров. << Конкуренту >> же нужно придерживаться xk набора товарных групп полученном соотношении для выпуска своей продукции. Если же игроки будут поступать иначе, они получат только худший результат. Предложенный в работе метод может быть применен в экономике для планирования товарного ассортимента фирмы.
Скачать презентацию РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ МЕТОДА БРАУНА — РОБИНСОНА
Игнатов.pptx