Решение задачи по геометрии на нахождение расстояния от

Решение задачи по геометрии на нахождение расстояния от точки до плоскости. Выполнил ученик 10 б класс Лицея № 180 Вершинин Иван

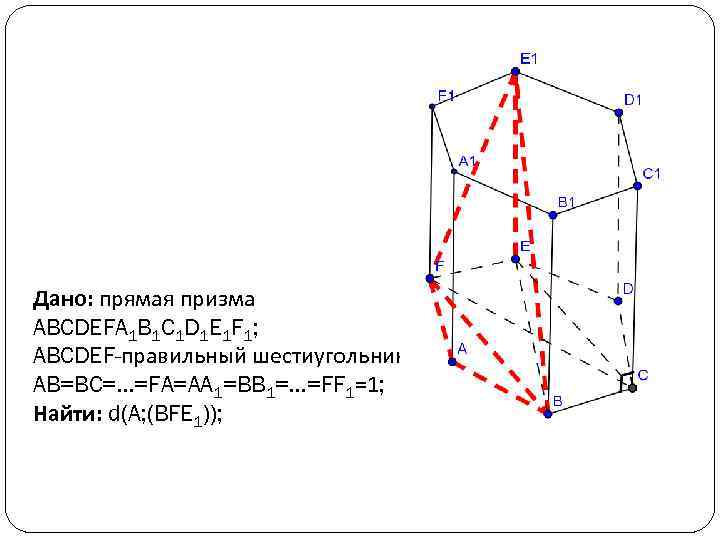Дано: прямая призма ABCDEFA 1 B 1 C 1 D 1 E 1 F 1; ABCDEF-правильный шестиугольник; AB=BC=…=FA=AA 1=BB 1=…=FF 1=1; Найти: d(A; (BFE 1));

Решение: 1)Рассмотрим четырехугольник FECB; FE=BC, FE ∥ BC ⇒FECB-параллелограмм (по IV призн. ); 2)В пар-ме FECB: EB=FC(так как диагонали правильного многоугольника) ⇒ FECB- прямоугольник( по признаку прямоугольника) ⇒FE ⊥FB(по опр. прямоугольника); 3) FF 1 ⊥(FBC)(по определению прямой призмы) ⇒FF 1 ⊥FB(по опр. прямой ⊥ плоскости); 4) FE ⊥FB FF 1 ⊥FB ⇒ FB ⊥(F 1 FE)(по призн. перпенд. прямой и плоскости) ⇒FB⊥FE 1 FE ⋂ FF 1 =F ( по опр. прямой ⊥ плоскости); 5)Следовательно △FBE 1 – прямоугольный. 6)Отрезок FB можно найти по теореме косинусов: ∠FAB=120°; FB²=FA²+AB²-2*FA*FB*cos ∠A; FB²=1²+1²-2*1*1*cos(π-60°); FB= 3. 7)По теореме Пифагора можно найти отрезок FE 1 : FE 1 ² =FE ²+EE 1²; FE 1²=1²+1² ⇒ FE 1= 2; 8)S △E 1 FB=0. 5*E 1 F*FB=0. 5 * 2* 3=0. 5 6; 9)S △FAB=0. 5*AF*AB*sin ∠A; S △FAB=0. 5*1*1*sin(π-60°)=0. 25 3.

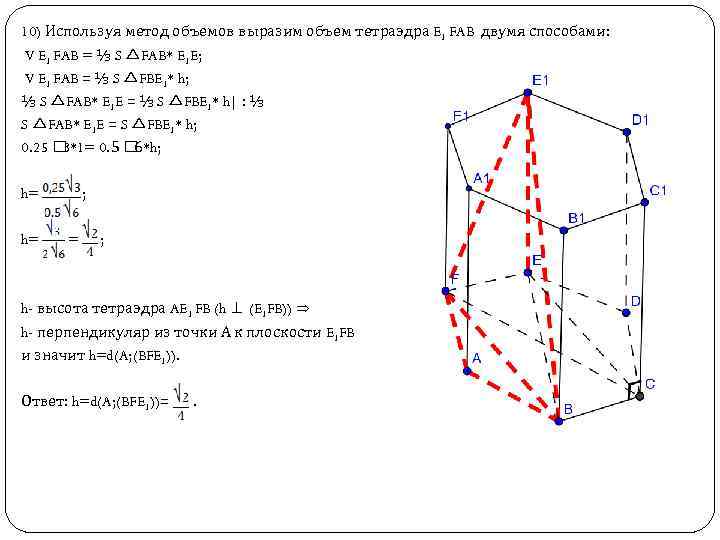10) Используя метод объемов выразим объем тетраэдра E 1 FAB двумя способами: V E 1 FAB = ⅓ S △FAB* E 1 E; V E 1 FAB = ⅓ S △FBE 1* h; ⅓ S △FAB* E 1 E = ⅓ S △FBE 1* h| : ⅓ S △FAB* E 1 E = S △FBE 1* h; 0. 25 3*1= 0. 5 6*h; h= h= ; h- высота тетраэдра AE 1 FB (h ⊥ (E 1 FB)) ⇒ h- перпендикуляр из точки А к плоскости E 1 FB и значит h=d(A; (BFE 1)). Ответ: h=d(A; (BFE 1))= .