Решение задач XXXV московской городской олимпиады Секция Компьютерная

Решение задач XXXV московской городской олимпиады. Секция «Компьютерная графика» 1) Построение тора 4) Образование тел вращения, заданных контурами 2) Сечение тора, построение контура N 5) Компоновка тел вращения в сборе 3) Построение конуса, построение контура М

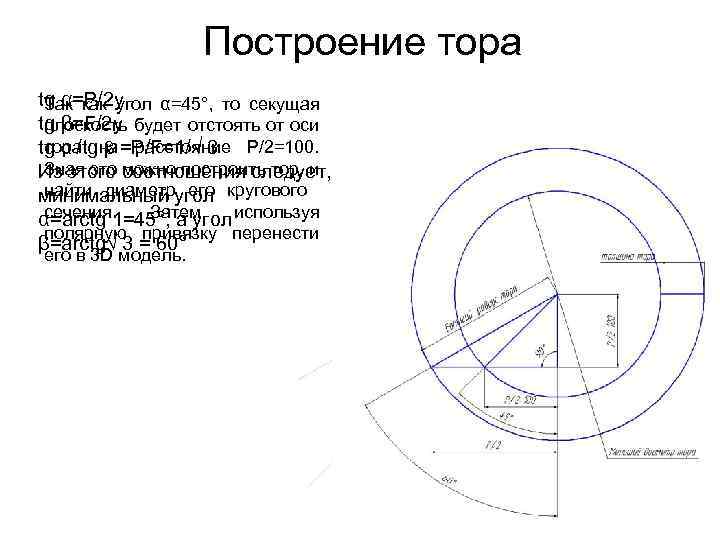Построение тора tg α=P/2 y Так как угол α=45°, то секущая tg β=F/2 y будет отстоять от оси плоскость тора β расстояние tg α /tgна =P/F=1/√ 3 Р/2=100. Зная это можно построить тор, и Из этого соотношения следует, что найти диаметр его минимальный угол кругового сечения. Затем α=arctg 1=45°, а угол используя полярную привязку перенести β=arctg√ 3 = 60° его в 3 D модель.

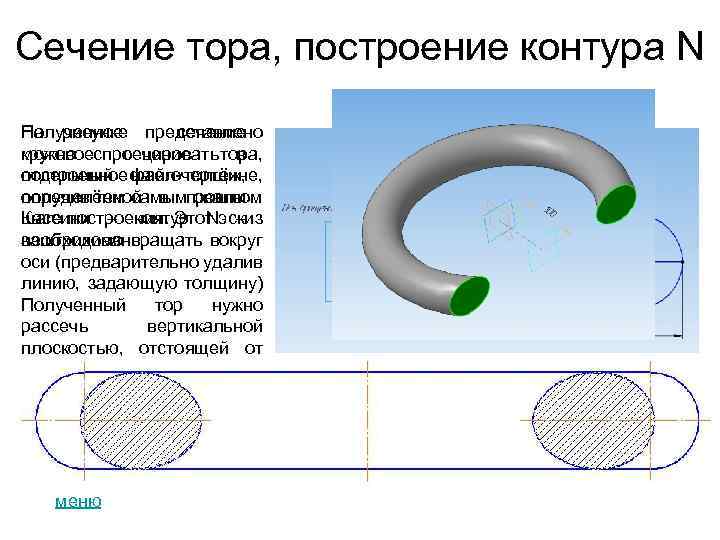Сечение тора, построение контура N Полученное сечение На рисунке представлено можно в круговоеспроецироватьтора, сечение отдельный на его толщине, построенное файл-чертёж, получив тем самым овалы определённой в прошлом Кассини – контур N – шаге построения. Этот эскиз заштрихован. необходимо вращать вокруг оси (предварительно удалив линию, задающую толщину) Полученный тор нужно рассечь вертикальной плоскостью, отстоящей от оси тора на 100. меню

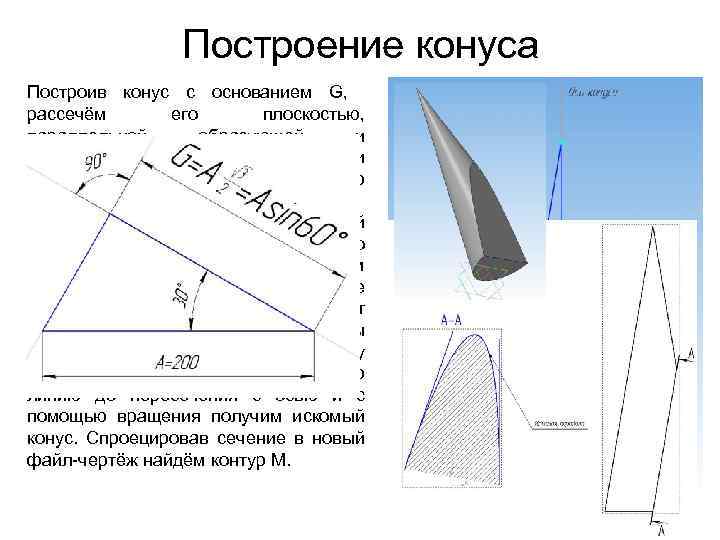Построение конуса Построив конус с основанием G, рассечём его плоскостью, параллельной образующей и проходящей через центр окружности основания, получим параболу – контур М. Далее необходимо найти неизвестный наклон образующей. Для этого построим две окружности радиусом К=1, 5 G с центрами в конце и середине диаметра G. Точка их пересечения даст вторую точку проекции параболы (наклон сечения равен наклону образующей). Продлим построенную линию до пересечения с осью и с помощью вращения получим искомый конус. Спроецировав сечение в новый файл-чертёж найдём контур М. Зная зависимость G от А можно построить величину G, приняв √ 3/2 как значение синуса 60°. Тогда А гипотенуза прямоугольного треугольника, а G его катет, противолежащий углу в 60°

Образование тел вращения, заданных контурами Тела вращения, заданные контурами М и N получаются аналогично тору. Однако для начала необходимо установить их взаимное расположение. Для этого проведём касательные прямые к контурам в заданных по чертежу точках (стандартная функция Компас). Совместив касательные поворотом сдвинем параболу чтобы точки касания параболы Тело N и овала совпали. Затем используя полярную привязку перенесём контуры по отдельности в 3 D и провращаем, получив тела М и N. меню Тело М

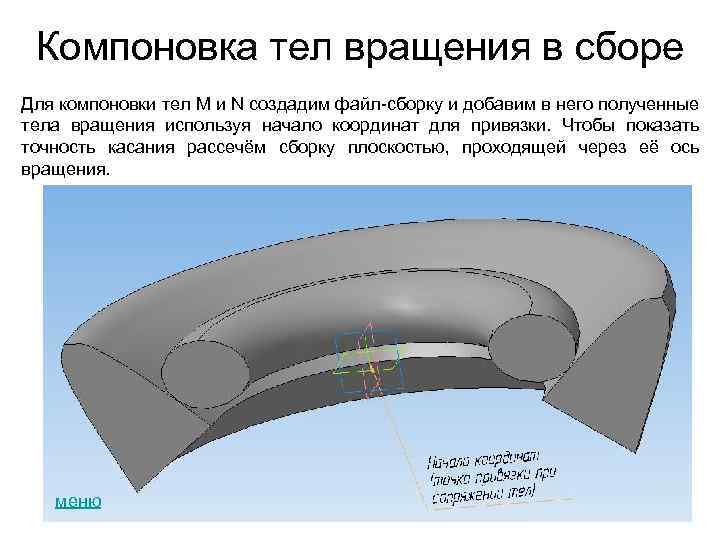Компоновка тел вращения в сборе Для компоновки тел М и N создадим файл-сборку и добавим в него полученные тела вращения используя начало координат для привязки. Чтобы показать точность касания рассечём сборку плоскостью, проходящей через её ось вращения. меню