Решение задач в целых числах Основы теории

«Решение задач в целых числах» (Основы теории)

• Число делится на 2 тогда и только тогда, когда его последняя цифра четна • Число делится на 3 тогда и тогда, когда сумма всех его цифр делится на 3 • Число делится на 4 тогда и только тогда, когда число, составленное из последних двух цифр его десятичной записи, идущих в том же порядке, делится на 4 • Число делится на 5 тогда и только тогда, когда оно оканчивается на 0 или 5 • Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9

• Число делится на 11 тогда и только тогда, когда разность суммы цифр, стоящих на нечетных местах, считая справа в десятичной записи данного числа, и суммы цифр, стоящих на четных мечтах в десятичной записи данного числа, делится на 11 Например, число 305 792 608 делится на 11, так как (8 + 6 + 9 + 5 + 3) – ( 0 + 2 + 7 + 0) = 22 22 – делится на 11 3

• Натуральное число, отличное от 1, называется простым, если у него нет натуральных делителей, отличных от 1 и него самого • Числа, отличные от 1 и не являющиеся простыми, называются составными • 1 не является ни простым, ни составным числом • Два числа, наибольший общий делитель которых равен 1, называются взаимно простыми

Каждое натуральное число n>1 имеет единственное (с точностью до порядка множителей) разложение на простые множители n = p 1 p 2 α 1 α 2· … p k αk Каноническое разложение числа n

Количество натуральных делителей числа n, записанного в канонической форме, равно (α 1 + 1) · (α 2 + 1) ·…·(αk + 1)

Любое целое число а можно поделить с остатком на любое ненулевое целое число b a = bq + r Сумма (произведение) чисел а и b дает тот же остаток при делении на число m, что и сумма (произведение) остатков чисел а и b при делении на число m

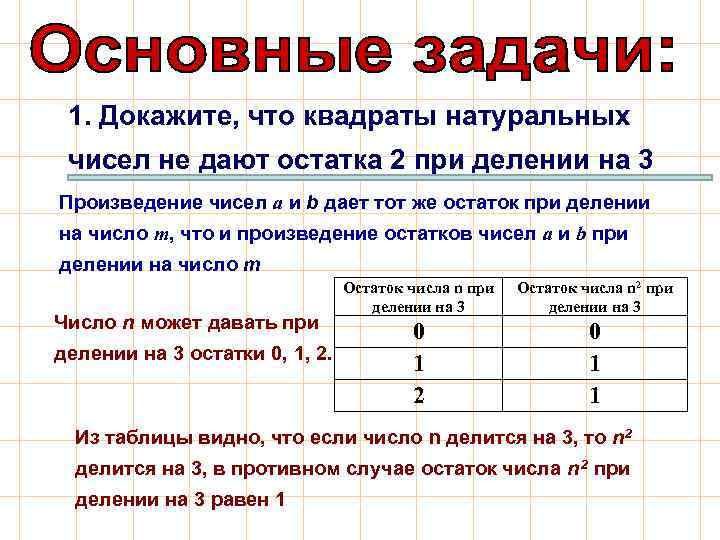1. Докажите, что квадраты натуральных чисел не дают остатка 2 при делении на 3 Произведение чисел а и b дает тот же остаток при делении на число m, что и произведение остатков чисел а и b при делении на число m Число n может давать при делении на 3 остатки 0, 1, 2. Остаток числа n при делении на 3 Остаток числа n 2 при делении на 3 0 1 2 0 1 1 Из таблицы видно, что если число n делится на 3, то n 2 делится на 3, в противном случае остаток числа n 2 при делении на 3 равен 1

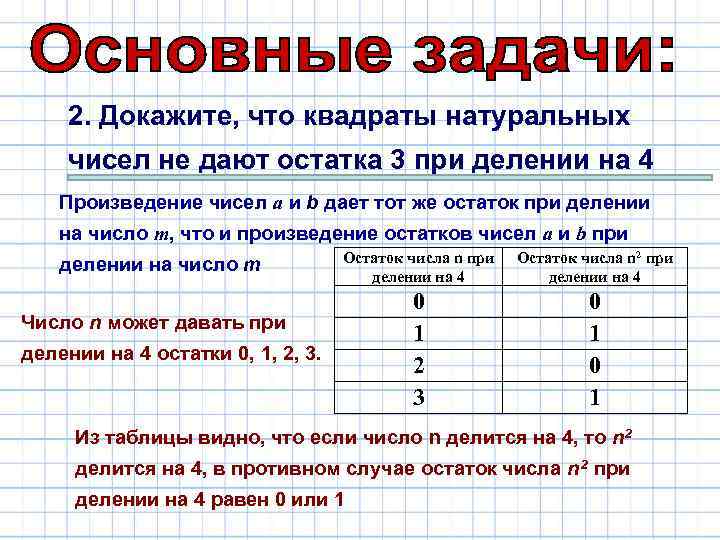2. Докажите, что квадраты натуральных чисел не дают остатка 3 при делении на 4 Произведение чисел а и b дает тот же остаток при делении на число m, что и произведение остатков чисел а и b при делении на число m Остаток числа n при делении на 4 Остаток числа n 2 при делении на 4 0 1 2 3 0 1 Число n может давать при делении на 4 остатки 0, 1, 2, 3. Из таблицы видно, что если число n делится на 4, то n 2 делится на 4, в противном случае остаток числа n 2 при делении на 4 равен 0 или 1

3. Докажите, что при любом целом а разность делится на 2 Из двух последовательных целых чисел а – 1 и а одно (и только одно) является четным. Произведение двух последовательных чисел делится на 2 4. Докажите, что при любом целом а разность делится на 3 Из трех последовательных целых чисел а – 1, а и а + 1 одно (и только одно) делится на 3. Произведение трех последовательных чисел делится на 3

5. Докажите, что при любом целом а разность делится на 5 Теперь можно рассмотреть пять случаев: a = 5 k, a = 5 k + 1, a = 5 k + 2, a = 5 k + 3, a = 5 k + 4 (k Z) В любом случае произведение делится на 5

6. Докажите, что при любом целом а разность делится на 7 Теперь можно рассмотреть семь случаев: a = 7 k, a = 7 k + 1, a = 7 k + 2, a = 7 k + 3, a = 7 k + 4, a = 7 k + 5, a = 7 k + 6 (k Z) В любом случае произведение делится на 7

Верно ли, что для любого целого а Делимости неверны, так как, например, не делится на 4 ? не делится на 6 не делится на 9 Делимость справедлива при простом n

При любом натуральном а и любом простом р разность делится на р Если а – любое натуральное число, р – любое простое число, то степень при делении на р может давать в остатке только 0 или 1. В частности, если а не делится на р, то разность делится на р

Упражнения: Найдите остаток от деления: на 101 на 29 Ответ: 1 Ответ: 7