 Решение задач С 2 ЕГЭ
Решение задач С 2 ЕГЭ
 1. Расстояние от точки до прямой
1. Расстояние от точки до прямой
 В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, стороны основания которой равны 1, а боковые ребра равны 2, найти расстояние от точки A до прямой BC 1. E 1 D 1 F 1 А 1 C 1 B 1 E Решение. Расстояние от точки до прямой есть длина перпендикуляра, опущенного из этой точки на прямую. АН – искомый перпендикуляр. D F С А Значит, ∆АВС 1 – тупоугольный и перпендикуляр АН падает на продолжение стороны ВС 1. В Н
В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, стороны основания которой равны 1, а боковые ребра равны 2, найти расстояние от точки A до прямой BC 1. E 1 D 1 F 1 А 1 C 1 B 1 E Решение. Расстояние от точки до прямой есть длина перпендикуляра, опущенного из этой точки на прямую. АН – искомый перпендикуляр. D F С А Значит, ∆АВС 1 – тупоугольный и перпендикуляр АН падает на продолжение стороны ВС 1. В Н
 2. Угол между прямыми
2. Угол между прямыми
 В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точка Е – середина ребра SD. Найти косинус угла между прямыми SB и AE. S Решение. Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых. E D С Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся. O А EO – средняя линия ∆BDS, EO||BS В
В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точка Е – середина ребра SD. Найти косинус угла между прямыми SB и AE. S Решение. Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых. E D С Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся. O А EO – средняя линия ∆BDS, EO||BS В
 3. Расстояние от точки до плоскости
3. Расстояние от точки до плоскости
 D 1 A 1 В единичном кубе ABCDA 1 B 1 C 1 D 1 найдите расстояние от точки А до плоскости ВDC 1 z C 1 А x A(1, 0, 0), B(1, 1, 0), D(0, 0, 0), C 1(0, 1, 1). B 1 С D В Решение. Введем прямоугольную систему координат с центром в точке D. Расстояние от точки (x 0, y 0, z 0)до плоскости, заданной уравнением Ax+By+Cz+D=0, ищется по формуле: y Составим уравнение плоскости DBC 1. Для этого решим систему уравнений:
D 1 A 1 В единичном кубе ABCDA 1 B 1 C 1 D 1 найдите расстояние от точки А до плоскости ВDC 1 z C 1 А x A(1, 0, 0), B(1, 1, 0), D(0, 0, 0), C 1(0, 1, 1). B 1 С D В Решение. Введем прямоугольную систему координат с центром в точке D. Расстояние от точки (x 0, y 0, z 0)до плоскости, заданной уравнением Ax+By+Cz+D=0, ищется по формуле: y Составим уравнение плоскости DBC 1. Для этого решим систему уравнений:
 4. Расстояние между скрещивающимися прямыми
4. Расстояние между скрещивающимися прямыми
 В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми АB и CB 1. z C 1 B 1 A 1 x Найдем расстояние от одной прямой до другой как расстояние от любой точки первой прямой до плоскости, содержащей вторую прямую, и проходящую через прямую параллельную первой прямой. АВ||А 1 В 1, то ρ(AB, CB 1)= ρ(AB, A 1 B 1 C)= ρ(A, A 1 B 1 C) C A Решение. y B Введем прямоугольную систему координат с центром в точке C. Составим уравнение плоскости А 1 B 1 C. Для этого решим систему уравнений:
В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найдите расстояние между прямыми АB и CB 1. z C 1 B 1 A 1 x Найдем расстояние от одной прямой до другой как расстояние от любой точки первой прямой до плоскости, содержащей вторую прямую, и проходящую через прямую параллельную первой прямой. АВ||А 1 В 1, то ρ(AB, CB 1)= ρ(AB, A 1 B 1 C)= ρ(A, A 1 B 1 C) C A Решение. y B Введем прямоугольную систему координат с центром в точке C. Составим уравнение плоскости А 1 B 1 C. Для этого решим систему уравнений:
 5. Угол между прямой и плоскостью
5. Угол между прямой и плоскостью
 z D S В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найти синус угла между прямой BD и плоскостью SBC. Решение. Введем прямоугольную систему координат с центром в точке D. y С А В x Составим уравнение плоскости BCS. Для этого решим систему уравнений:
z D S В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найти синус угла между прямой BD и плоскостью SBC. Решение. Введем прямоугольную систему координат с центром в точке D. y С А В x Составим уравнение плоскости BCS. Для этого решим систему уравнений:
 6. Угол между двумя плоскостями
6. Угол между двумя плоскостями
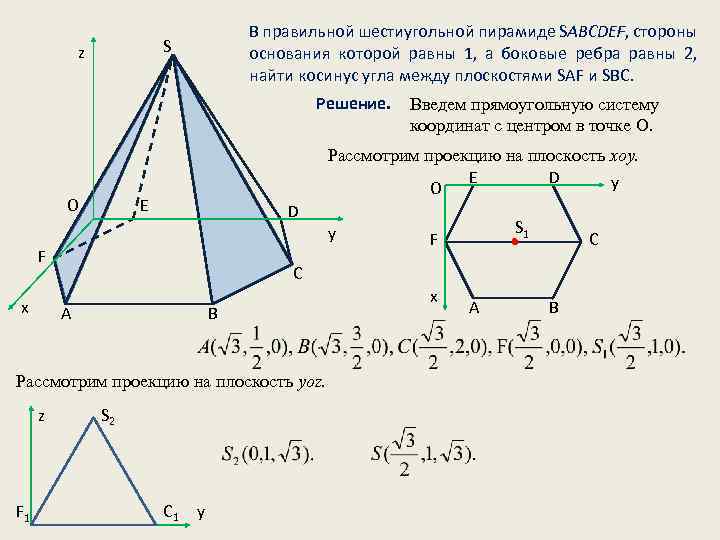 В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найти косинус угла между плоскостями SAF и SBC. S z Решение. O Рассмотрим проекцию на плоскость xoy. E D y O E D y F x B Рассмотрим проекцию на плоскость yoz. F 1 S 1 F C C А z Введем прямоугольную систему координат с центром в точке O. S 2 C 1 y x A B
В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найти косинус угла между плоскостями SAF и SBC. S z Решение. O Рассмотрим проекцию на плоскость xoy. E D y O E D y F x B Рассмотрим проекцию на плоскость yoz. F 1 S 1 F C C А z Введем прямоугольную систему координат с центром в точке O. S 2 C 1 y x A B
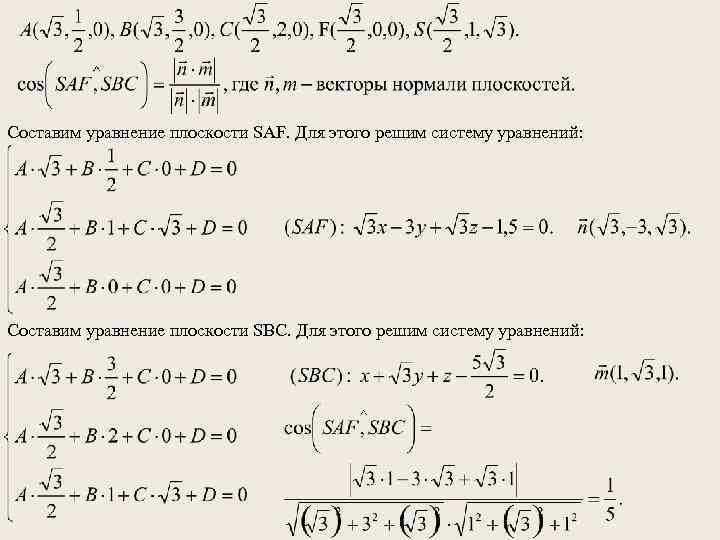 Составим уравнение плоскости SAF. Для этого решим систему уравнений: Составим уравнение плоскости SBC. Для этого решим систему уравнений:
Составим уравнение плоскости SAF. Для этого решим систему уравнений: Составим уравнение плоскости SBC. Для этого решим систему уравнений:
 7. Сечения многогранников
7. Сечения многогранников
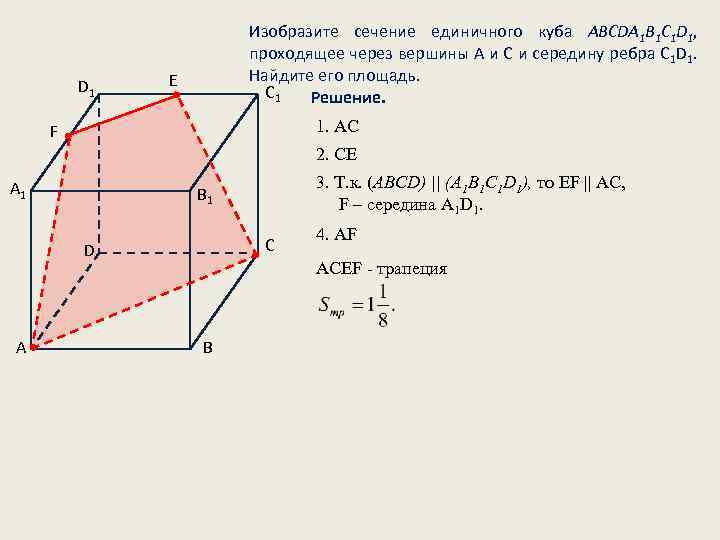 D 1 Изобразите сечение единичного куба ABCDA 1 B 1 C 1 D 1, проходящее через вершины А и С и середину ребра С 1 D 1. Найдите его площадь. C 1 Решение. Е 1. АС F 2. СЕ A 1 С D А 3. Т. к. (ABCD) || (A 1 B 1 C 1 D 1), то EF || AC, F – середина A 1 D 1. B 1 4. AF ACEF - трапеция В
D 1 Изобразите сечение единичного куба ABCDA 1 B 1 C 1 D 1, проходящее через вершины А и С и середину ребра С 1 D 1. Найдите его площадь. C 1 Решение. Е 1. АС F 2. СЕ A 1 С D А 3. Т. к. (ABCD) || (A 1 B 1 C 1 D 1), то EF || AC, F – середина A 1 D 1. B 1 4. AF ACEF - трапеция В


