РЕШЕНИЕ ЗАДАЧ ПРИ ПАРНОЙ ИГРЕ С НУЛЕВОЙ СУММОЙ

РЕШЕНИЕ ЗАДАЧ ПРИ ПАРНОЙ ИГРЕ С НУЛЕВОЙ СУММОЙ

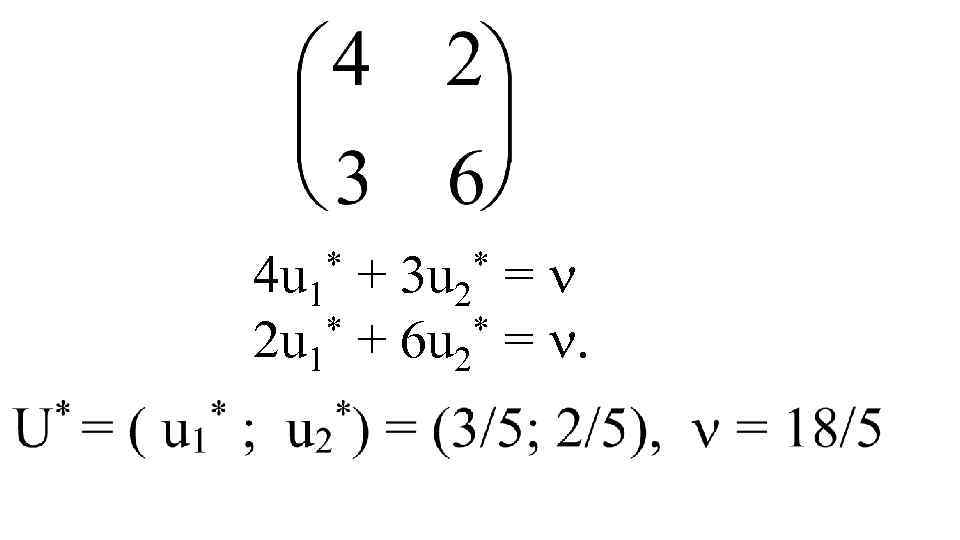* 4 u 1 * 2 u 1 + + * 3 u 2 * 6 u 2 = = .

Игры с природой

• Правило максимакса(критерий крайнего оптимизма) • Правило максимина (Вальда) • Правило Лапласа • Правило минимакса (Сэвиджа) • Критерий Гурвица.

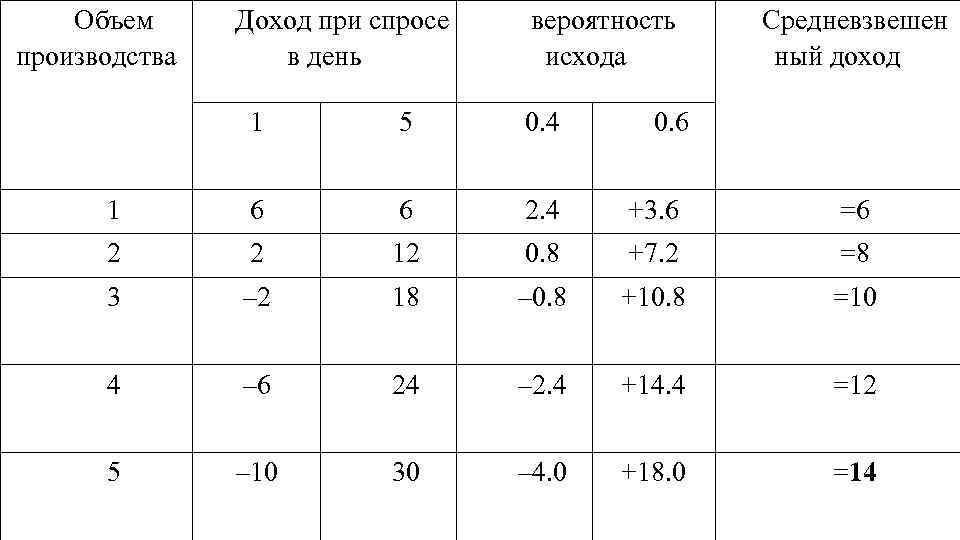Объем производства Доход при спросе в день вероятность исхода Средневзвешен ный доход 1 5 0. 4 0. 6 1 6 6 2. 4 +3. 6 =6 2 2 12 0. 8 +7. 2 =8 3 – 2 18 – 0. 8 +10. 8 =10 4 – 6 24 – 2. 4 +14. 4 =12 5 – 10 30 – 4. 0 +18. 0 =14

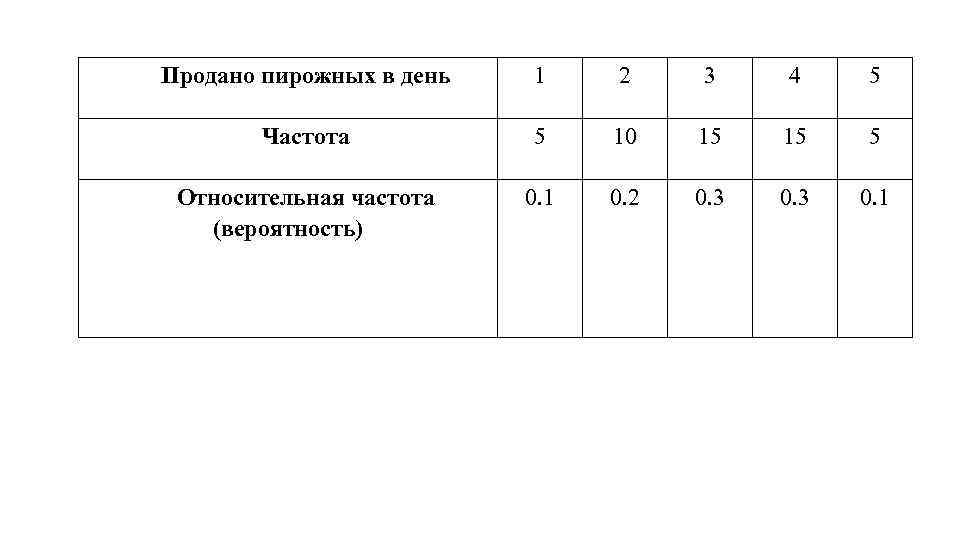Продано пирожных в день 1 2 3 4 5 Частота 5 10 15 15 5 Относительная частота (вероятность) 0. 1 0. 2 0. 3 0. 1

Правила принятия решений с использованием численных значений вероятностей исходов. • Правило максимальной вероятности – максимизация наиболее вероятных доходов. • Оптимизация математического ожидания (правило Байеса)

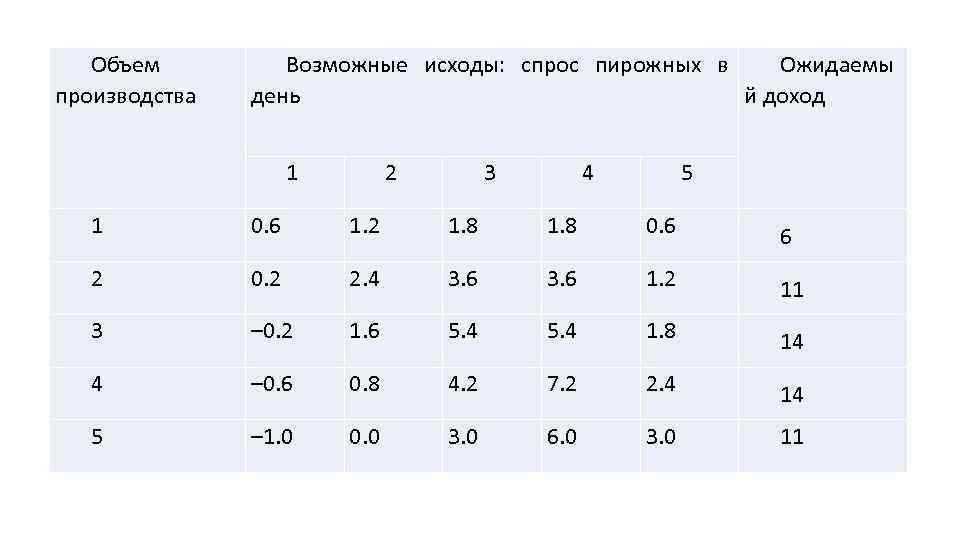Объем производства Возможные исходы: спрос пирожных в Ожидаемы день й доход 1 2 3 4 5 1 0. 6 1. 2 1. 8 0. 6 6 2 0. 2 2. 4 3. 6 1. 2 11 3 – 0. 2 1. 6 5. 4 1. 8 14 4 – 0. 6 0. 8 4. 2 7. 2 2. 4 14 5 – 1. 0 0. 0 3. 0 6. 0 3. 0 11

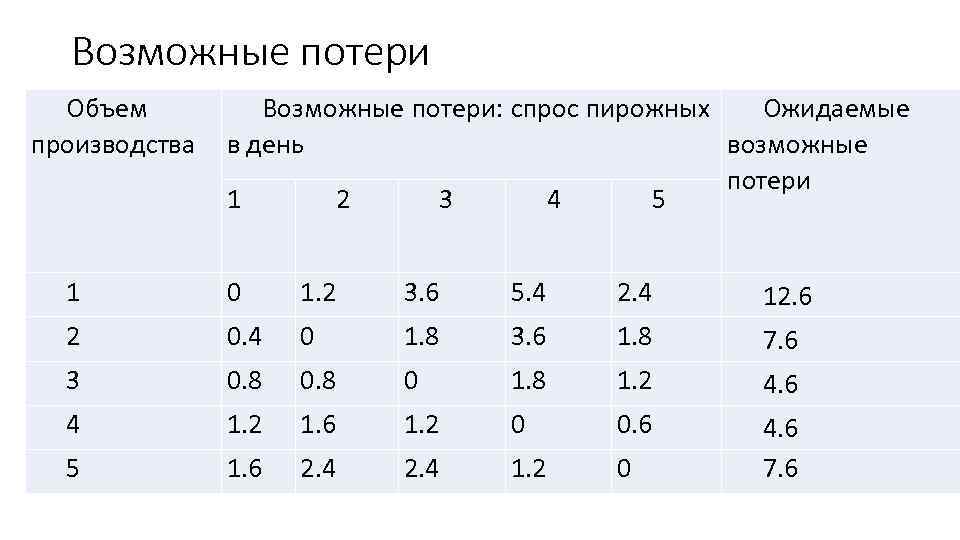Возможные потери Объем Возможные потери: спрос пирожных Ожидаемые производства в день возможные потери 1 2 3 4 5 1 0 1. 2 3. 6 5. 4 2. 4 12. 6 2 0. 4 0 1. 8 3. 6 1. 8 7. 6 3 0. 8 0 1. 8 1. 2 4. 6 4 1. 2 1. 6 1. 2 0 0. 6 5 1. 6 2. 4 1. 2 0 4. 6 7. 6

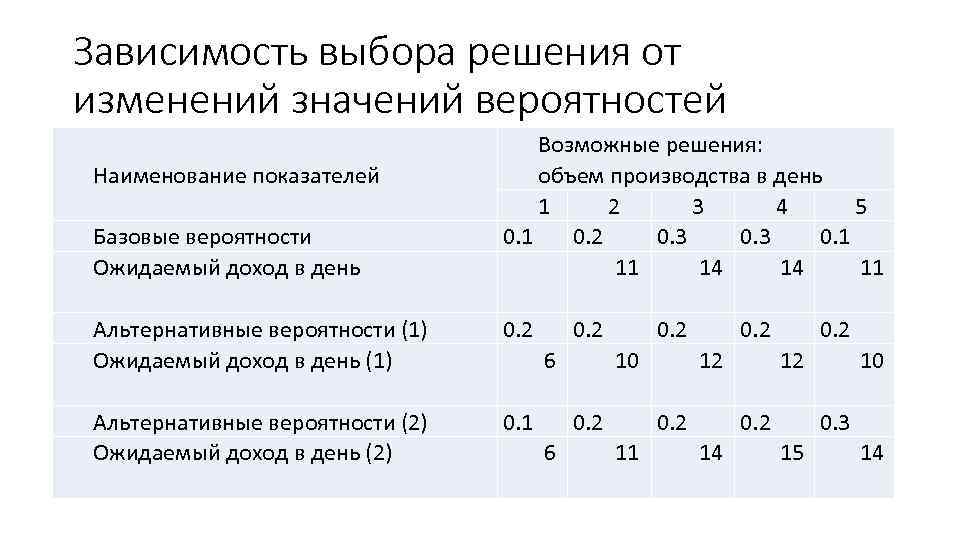Зависимость выбора решения от изменений значений вероятностей Наименование показателей Базовые вероятности Ожидаемый доход в день Возможные решения: объем производства в день 1 2 3 4 5 0. 1 0. 2 0. 3 0. 1 11 14 14 11 Альтернативные вероятности (1) Ожидаемый доход в день (1) 0. 2 Альтернативные вероятности (2) Ожидаемый доход в день (2) 0. 2 0. 1 6 0. 2 10 0. 2 6 0. 2 12 0. 2 11 0. 2 12 0. 2 14 10 0. 3 15 14

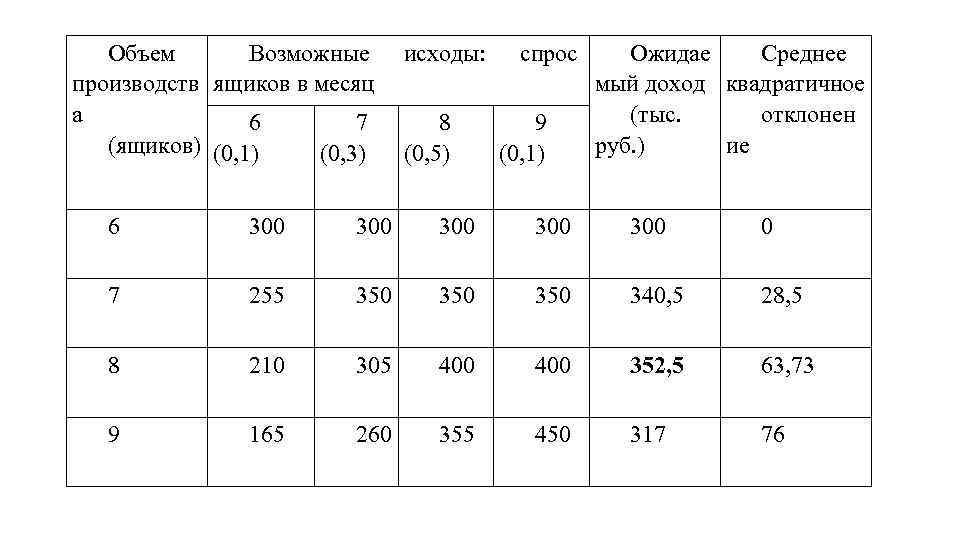Объем Возможные производств ящиков в месяц а 6 7 (ящиков) (0, 1) (0, 3) исходы: 8 (0, 5) спрос 9 (0, 1) Ожидае Среднее мый доход квадратичное (тыс. отклонен руб. ) ие 6 300 300 300 0 7 255 350 350 340, 5 28, 5 8 210 305 400 352, 5 63, 73 9 165 260 355 450 317 76