РЕШЕНИЕ ЗАДАЧ ПО ОПТИМИЗАЦИИ 1 Краткие теоретические сведения

РЕШЕНИЕ ЗАДАЧ ПО ОПТИМИЗАЦИИ 1. Краткие теоретические сведения 2. Метод линейного программирования 3. Построение математической модели исходной задачи на max или min 4. Требования к переменным 5. Методы решения: графический, Простой перебор, Направленный перебор, Симплексметод 6. Двойственная задача линейного программирования

Задачи оптимизации Ежедневно специалисты в области экономики и менеджмента сталкиваются с задачами оптимизации. Это и расчет фонда заработной платы, и планирование производственной программы, рекламной компании, и еще множество задач, решаемых с помощью методов оптимизации. Наиболее легкими и показательными являются задачи линейной оптимизации.

Метод линейного программирования Для решения таких задач разработаны специальные методы линейного программирования, которые особенно широко применяются в экономике. Линейное программирование – это раздел высшей математики, занимающийся разработкой методов отыскания экстремальных значений линейной функции, на неизвестные которой наложены линейные ограничения.

Признаки задач линейного программирования 1. Комплекс неотрицательных независимых переменных. 2. Только одна цель, служащая функцией переменных. 3. Наличие ограничений, налагающих пределы на достижение цели. 4. Линейный характер количественных соотношений.

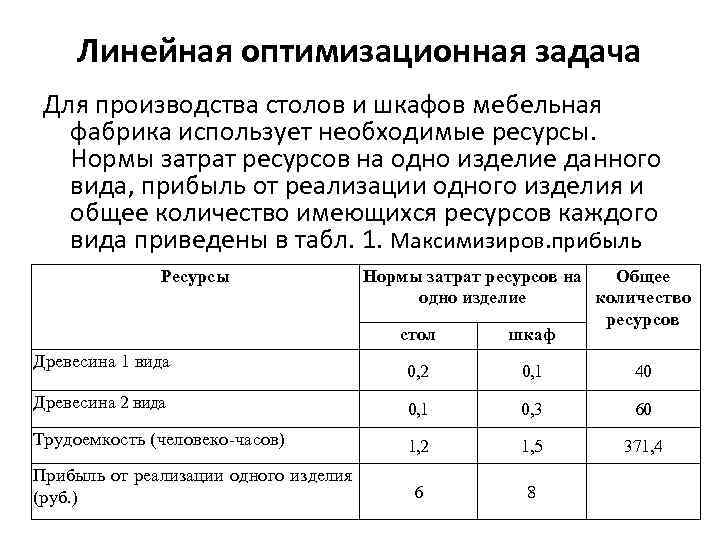Линейная оптимизационная задача Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в табл. 1. Максимизиров. прибыль Ресурсы Древесина 1 вида Нормы затрат ресурсов на Общее одно изделие количество ресурсов стол шкаф 0, 2 0, 1 40 Древесина 2 вида 0, 1 0, 3 60 Трудоемкость (человеко-часов) 1, 2 1, 5 371, 4 6 8 Прибыль от реализации одного изделия (руб. )

Решение Для решения этой задачи необходимо построить математическую модель. Процесс построения модели можно начать с ответа на следующие три вопроса: 1. Для определения каких величин строится модель? 2. В чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные? 3. Каким ограничениям должны удовлетворять неизвестные?

Решение Переменными являются: х1 - количество столов, х2 - количество шкафов Суммарная прибыль от производства столов и шкафов равна z = 6*х1 +8*х2. Целью фабрики является определение среди всех допустимых значений х1 и х2 таких, которые максимизируют суммарную прибыль, т. е. целевую функцию z

Ограничения, которые налагаются на х1 и х2 : • объем производства шкафов и столов не может быть отрицательным, следовательно: х1, х2 0. затрат древесины на столы и шкафы не могут превосходить максимально возможный запас данного исходного продукта, следовательно: 0, 2 х1 + 0, 1 х2 40, 0, 1 х1 +0, 3 х2 60. Кроме того, ограничение на трудоемкость: она не превышает количества затрачиваемых труд. ресурсов 1, 2 х1 + 1, 5 х2 371, 4.

Математическая модель Таким образом, математическая модель данной задачи имеет следующий вид: Максимизировать функцию: z = 6 * х 1 + 8 * х2 при следующих ограничениях: 0, 2 х1 + 0, 1 х2 40 0, 1 х1 + 0, 3 х2 60 1, 2 х1 + 1, 5 х2 371, 4 Данная модель является линейной, т. к. целевая функция и ограничения линейно зависят от переменных.

Решение Таким образом, множество возможных значений объемов выпуска столов и шкафов (Х 1 , Х 2 ), или, в других терминах, множество А, задающее ограничения на параметр управления в общей оптимизационной задаче, представляет собой пересечение двух треугольников, т. е. выпуклый четырехугольник, показанный на рис. 1. Три его вершины очевидны - это (0, 0), (200, 400) и (600, 200). Четвертая - это пересечение двух прямых - границ треугольников на рис. 1 и рис. 2, т. е. решение системы уравнений (ограничения).

Решение Решая систему уравнений получим четвертую вершину четырехугольника - это (102; 166). Найден максимум линейной функции на выпуклом многоугольнике. Основная идея линейного программирования состоит в том, что максимум достигается в вершинах многоугольника. В общем случае - в одной вершине, и это единственная точка максимума. Иногда, в частном случае- в двух, и тогда отрезок, их соединяющий, тоже состоит из точек максимума.

Решение Таким образом, оптимальный выпуск таков: 102 стола и 166 шкафов. При этом используется весь материал и все трудовые ресурсы, а прибыль равна: 6*102 + 8*166 = 1940 руб.

Двойственная задача Каждой задаче линейного программирования соответствует так называемая двойственная задача. В ней по сравнению с исходной задачей строки переходят в столбцы, неравенства меняют знак, вместо максимума ищется минимум (или наоборот, вместо минимума максимум). Задача, двойственная к двойственной - эта сама исходная задача. Сравним исходную задачу (слева) и двойственную к ней (справа): 6 Х 1 + 8 Х 2 → max , 0, 2 Х 1 + 0, 1 Х 2 ≤ 40 , 0, 1 Х 1 + 0, 3 Х 2 ≤ 60 , 1, 2 Х 1 + 1, 5 Х 2 ≤ 371, 4 Х 1 ≥ 0 , Х 2 ≥ 0 40 W 1 + 60 W 2 + 371, 4 W 3→ min , 0, 2 W 1 + 0, 1 W 2 + 1, 2 W 3 ≥ 6, 0, 1 W 1 + 0, 3 W 2 + 1, 5 W 3 ≥ 8, W 1 ≥ 0, W 2 ≥ 0.

Двойственная задача Почему двойственная задача столь важна? Доказано, что оптимальные значения целевых функций в исходной и двойственной задачах совпадают (т. е. максимум в исходной задаче совпадает с минимумом в двойственной). При этом оптимальные значения W 1, W 2 и W 3 показывают стоимость материала и труда соответственно, если их оценивать по вкладу в целевую функцию. Чтобы не путать с рыночными ценами этих факторов производства, W 1 W 2 и W 3 называют "объективно обусловленными оценками" сырья и рабочей силы (теневыми ценами).

Область применения метода Задачи распределения ресурсов. Они возникают, если есть набор работ, которые нужно выполнить, а наличных ресурсов для выполнения каждой работы наилучшим образом не хватает. Задача о смесях (рецептура кормов, диета). Оптимальный раскрой материалов. Оптимизация маршрутов перевозок (транспортная задача) и т. д.