РЕШЕНИЕ ЗАДАЧ ПО ГЕОМЕТРИИ Ученицы 10 Б класса

Зарегистрируйтесь, чтобы просмотреть полный документ!

РЕШЕНИЕ ЗАДАЧ ПО ГЕОМЕТРИИ Ученицы 10 «Б» класса лицея № 180 Суворовой Александры

Условие задачи: Дано: ABCD – квадрат. О – центр пересечения диагоналей. OM ⊥ к плоскости квадрата = 12, сторона квадрата = 8. Найти: 1) d (M; АВ); 2) (AM; АО); 3) (AM; AB); 4) (AM; (ABC)); 5) (AMB; (ABC)).

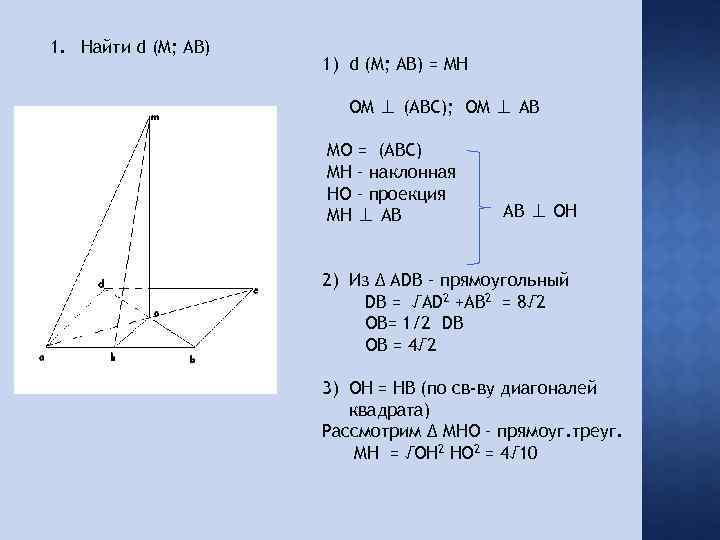
1. Найти d (M; AB) 1) d (M; АВ) = MH OM ⊥ (ABC); OM ⊥ AB MO = (ABC) MH – наклонная HO – проекция MH ⊥ AB AB ⊥ OH 2) Из Δ ADB – прямоугольный DB = √AD 2 +AB 2 = 8√ 2 OB= 1/2 DB OB = 4√ 2 3) OH = HB (по св-ву диагоналей квадрата) Рассмотрим Δ MHO – прямоуг. треуг. MH = √OH 2 HO 2 = 4√ 10

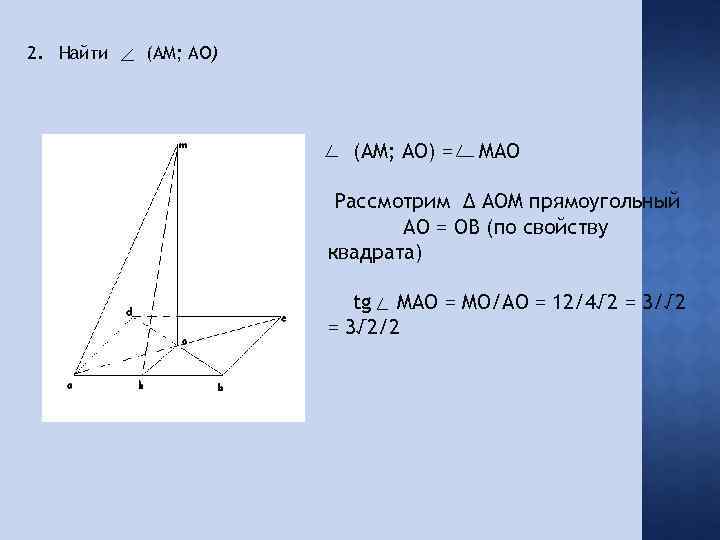
2. Найти (AM; AO) = MAO Рассмотрим Δ AOM прямоугольный AO = OB (по свойству квадрата) tg MAO = MO/AO = 12/4√ 2 = 3/√ 2 = 3√ 2/2

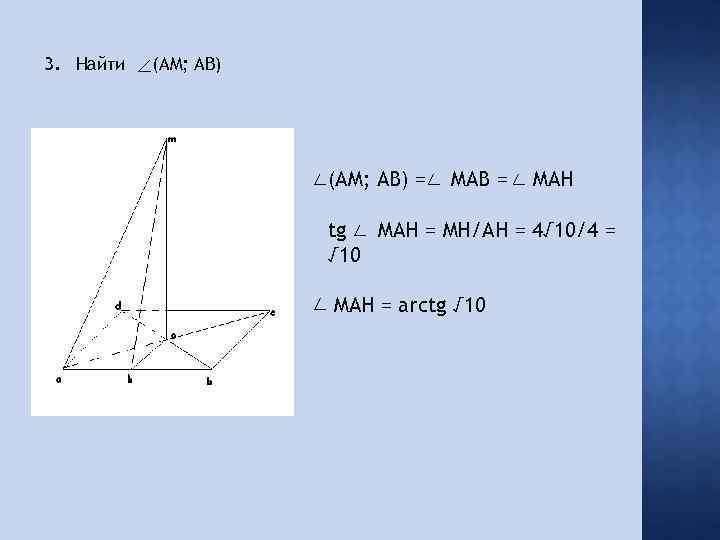
3. Найти (AM; AB) = MAB = MAH tg MAH = MH/AH = 4√ 10/4 = √ 10 MAH = arctg √ 10

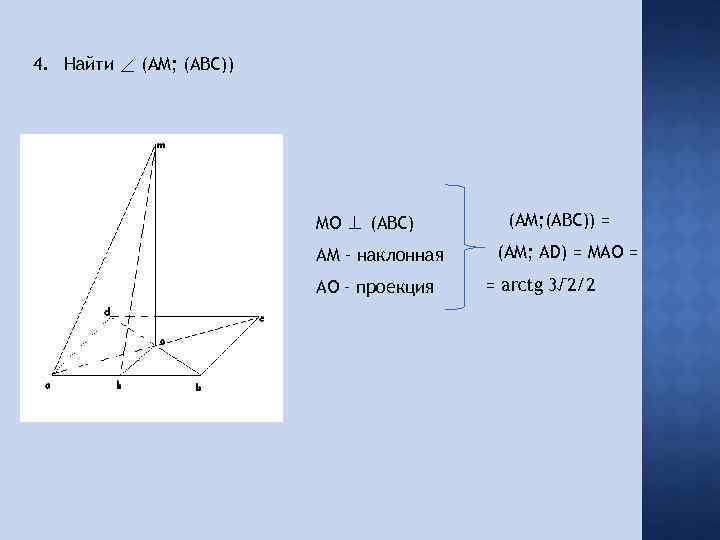
4. Найти (AM; (ABC)) MO ⊥ (ABC) AM – наклонная AO – проекция (AM; (ABC)) = (AM; AD) = MAO = = arctg 3√ 2/2

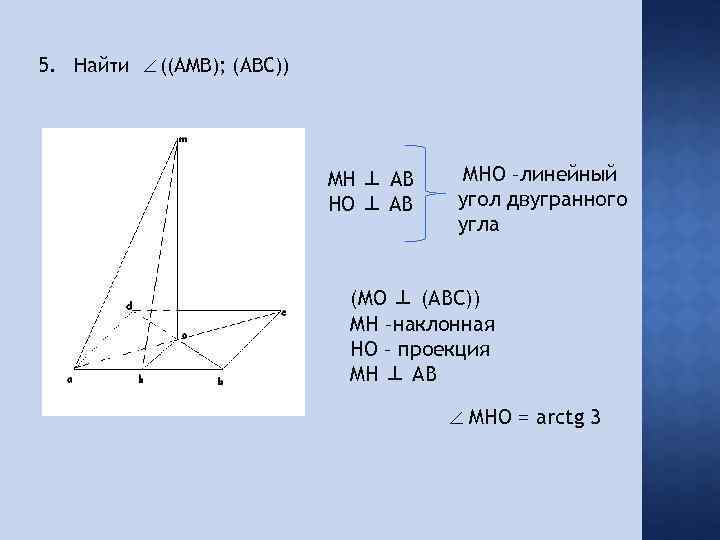
5. Найти ((AMB); (ABC)) MH ⊥ AB HO ⊥ AB MHO –линейный угол двугранного угла (MO ⊥ (ABC)) MH –наклонная HO – проекция MH ⊥ AB MHO = arctg 3

Скачать презентацию РЕШЕНИЕ ЗАДАЧ ПО ГЕОМЕТРИИ Ученицы 10 Б класса

Суворова.pptx

Количество слайдов: 7