 Решение уравнений и систем уравнений
Решение уравнений и систем уравнений
 Повышенный уровень сложности:
Повышенный уровень сложности:
 Задание 1; решите систему уравнений: 1) 2) Подставляем: Ответ:
Задание 1; решите систему уравнений: 1) 2) Подставляем: Ответ:
 Решите систему уравнений:
Решите систему уравнений:
 Задание 3; решите систему уравнений: Ответ:
Задание 3; решите систему уравнений: Ответ:
 Решите систему уравнений:
Решите систему уравнений:
 Задание 4; решите уравнение: Группируем: или или
Задание 4; решите уравнение: Группируем: или или
 Решите уравнение:
Решите уравнение:
 Задание 5; решите уравнение: Заменяем: Ответ:
Задание 5; решите уравнение: Заменяем: Ответ:
 Решите уравнение:
Решите уравнение:
 Задание 6; решите систему уравнений: Заменим: Ответ:
Задание 6; решите систему уравнений: Заменим: Ответ:
 Решите систему уравнений:
Решите систему уравнений:
 Задание 7; решите систему уравнений: Ответ: 1+9=10
Задание 7; решите систему уравнений: Ответ: 1+9=10
 Решите систему уравнений:
Решите систему уравнений:
 Высокий уровень сложности:
Высокий уровень сложности:
 Задание 1; решите уравнение: Вносим x в скобку: или Ответ:
Задание 1; решите уравнение: Вносим x в скобку: или Ответ:
 Решите уравнение:
Решите уравнение:
 . Задание 2; Найдите x+y+z: Ответ:
. Задание 2; Найдите x+y+z: Ответ:
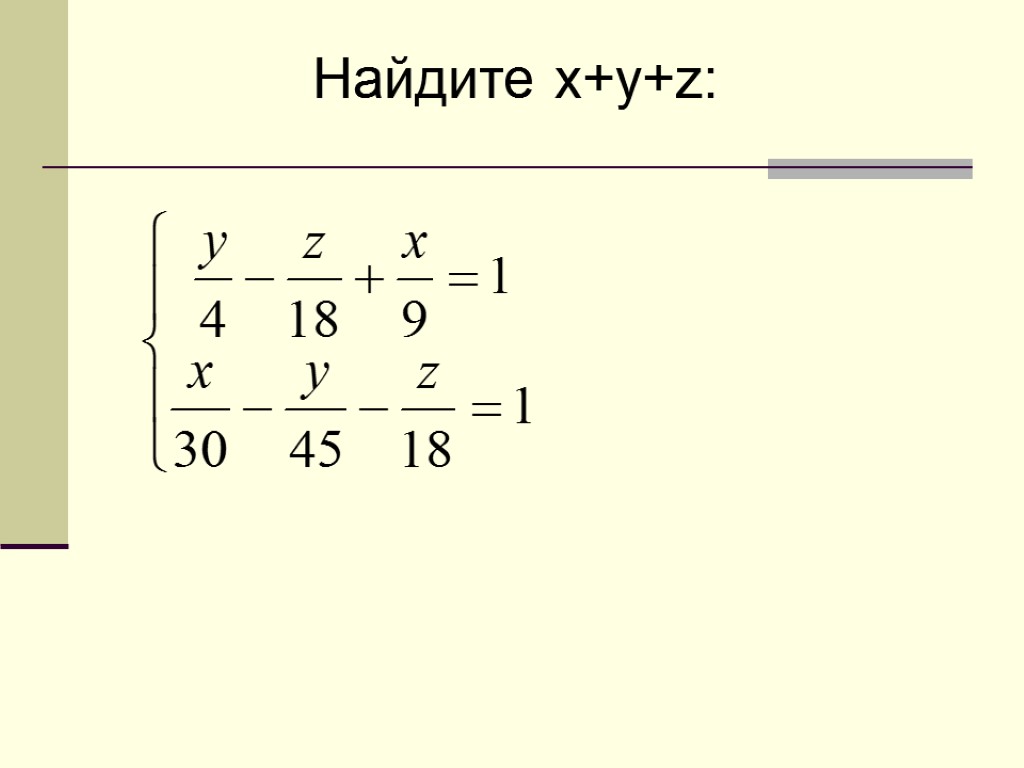 Найдите x+y+z:
Найдите x+y+z:
 Задание 3; Найдите все отрицательные значения m, при которых система уравнений не имеет решений: Ответ:
Задание 3; Найдите все отрицательные значения m, при которых система уравнений не имеет решений: Ответ:
 Найдите все отрицательные значения m, при которых система уравнений не имеет решений:
Найдите все отрицательные значения m, при которых система уравнений не имеет решений:
 . Задание 4; Докажите, что уравнение не имеет корней: Из этого следует, что x одновременно должен быть = 1 и 3, чтобы получился 0, а такого просто не может быть, чтобы одна переменная имела 2 значения. Поэтому уравнение не имеет решений.
. Задание 4; Докажите, что уравнение не имеет корней: Из этого следует, что x одновременно должен быть = 1 и 3, чтобы получился 0, а такого просто не может быть, чтобы одна переменная имела 2 значения. Поэтому уравнение не имеет решений.
 Докажите, что уравнение не имеет корней:
Докажите, что уравнение не имеет корней:















































