Решение уравнений и систем уравнений 1 Постановка

Решение уравнений и систем уравнений 1

Постановка задачи § Задана система уравнений: (1) § Функции могут иметь произвольный вид: § Могут быть линейными § Не заданными аналитически Ex 1. Ex 2. 2

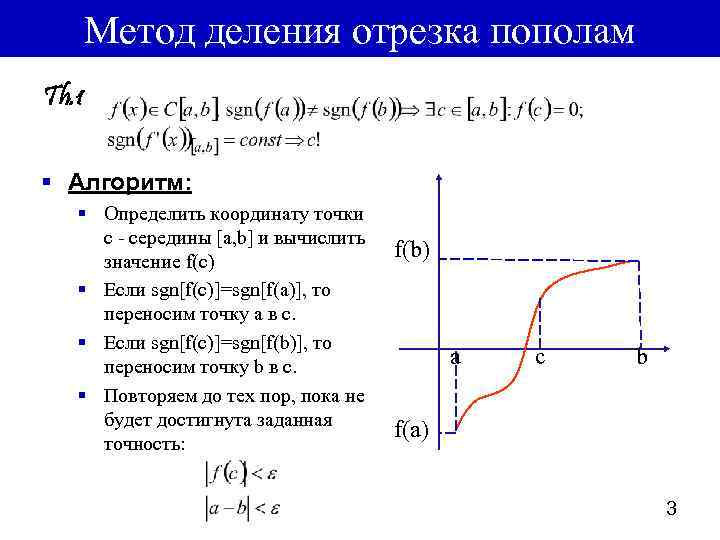Метод деления отрезка пополам Th. 1 § Алгоритм: § Определить координату точки с - середины [a, b] и вычислить значение f(c) § Если sgn[f(c)]=sgn[f(a)], то переносим точку а в с. § Если sgn[f(c)]=sgn[f(b)], то переносим точку b в с. § Повторяем до тех пор, пока не будет достигнута заданная точность: f(b) a c b f(a) 3

Численное решение СЛАУ. Постановка задачи (2) - невырожденная квадратная матрица - вектор-столбец решений - вектор-столбец правой части 4

Прямые методы § Метод Крамера (3) - определитель матрицы, полученной заменой в А i-го столбца на столбец правой части § Метод Гаусса Прямой ход: исключением из всех уравнений, начиная со второго, x 1, начиная с третьего – х2, … сводим матрицу А к треугольной (4) Обратный ход: определение элементов вектора x, начиная с последнего 5

Прямые методы § Метод Гаусса. LU-разложение. (5) Это представление матрицы А называется LU-разложением. Прямой ход метода Гаусса является LU-разложением. 6

Прямые методы § Метод Гаусса. LU-разложение. Если А представима в виде LU-разложения, то (6) Th. 2 Если все главные миноры А отличны от 0, то существует LU-разложение А 7

Итерационные методы § Метод простой итерации (7) § Алгоритм: § Выбрать произвольный вектор x 0 (обычно выбирают нулевой вектор) § Рассчитать элементы итерационной последовательности по формуле (8) Если предел итерационной последовательности существует, говорят о сходимости итераций 8

Определения Def. 1. Норма вектора Def. 2. Норма матрицы Def. 3. Собственные числа и собственные векторы Пусть . Тогда х – собственный вектор, - собственное число 9

Достаточное условие сходимости метода простой итерации Th. 3 Итерационный процесс (8) сходится к решению со скоростью геометрической прогрессии, если выполняется условие Доказательство - точное решение q. e. d. 10

Критерий сходимости метода простой итерации Th. 4 Для сходимости итерационного процесса необходимо и достаточно, чтобы все собственные числа матрицы В по абсолютной величине были меньше единицы Следствие из Th. 3 - заданная точность. Число итераций (9) Число вычислительных операций для итерационного алгоритма а для метода Гаусса. В реальных задачах I<

Численное решение нелинейных уравнений и систем уравнений Система нелинейных уравнений (10) путем эквивалентных преобразований может быть представлена в виде (11) Поставим в соответствие системе (11) итерационный процесс, т. е. процесс последовательного приближения к решению (12) 12

Сжимающее отображение. Определения Def. 4. Отображение – правило, по которому каждому элементу х некоторого множества Х ставится в соответствие элемент y множества Y ( X может совпадать с Y). При этом говорят, что отображение действует из множества X в Y. Если множества X и Y совпадают, то отображение преобразует множество Х в себя Def. 5. Область Ω называется выпуклой, если Ex. 4. не выпуклая область Def. 6. Отображение в замкнутой выпуклой области Ω сжимающее, если - расстояние между элементами множества 13

Теоремы о сжимающем отображении Th. 5. (Принцип сжимающих отображений) Всякое сжимающее отображение имеет одну и только одну неподвижную точку Th. 6. Последовательность если отображение , порожденная итерационным процессом сходится к решению системы уравнений , является сжимающим. При этом справедливо: Доказательство Def. 6 q. e. d. 14

Теоремы о сжимающем отображении Th. 7. (Принцип сжимающих отображений) Пусть - выпуклая область. Пусть компоненты F имеют непрерывные производные первого порядка. Пусть норма матрицы Якоби Тогда отображение v = F(u) – сжимающее в области Ω 15

Метод Ньютона Построим итерационную последовательность, исходя из следующих соображений. 16