Решение показательных уравнений В 5 Основное правило

Решение показательных уравнений В 5

Основное правило: Если в показательном уравнении с обеих сторон стоит одинаковое основание, то его мы упускаем, а показатели степени приравниваем. Если в правой части уравнения стоит число, то его мы представляем в виде степени с основанием, стоящим в левой части

Основные формулы:

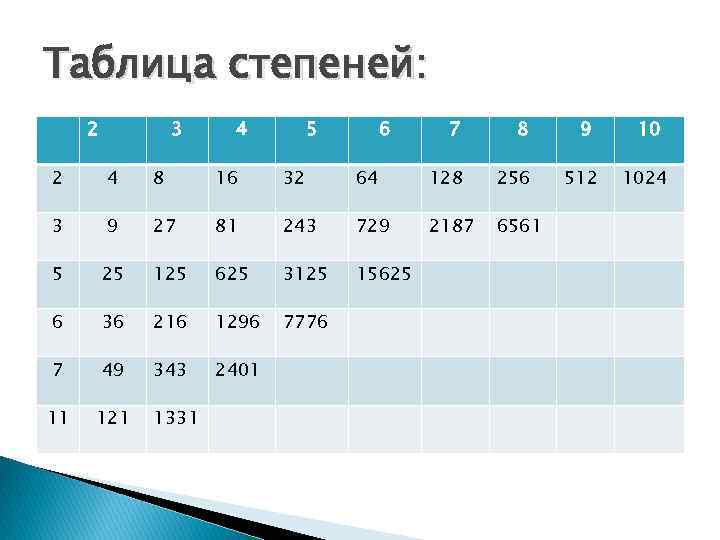Таблица степеней: 2 3 4 5 6 7 8 2 4 8 16 32 64 128 256 3 9 27 81 243 729 2187 6561 5 25 125 625 3125 15625 6 36 216 1296 7776 7 49 343 2401 11 121 1331 9 10 512 1024

Найдите корень уравнения Решение: В нашем случае 64=2 Имеем: 2 =2 Тогда по правилу мы основание можем опустить и получим линейное уравнение 4 -2 х=6 Решая его получим х=-1

Упуская основания, получаем Х-7=-3, или х=4 Ответ: 4

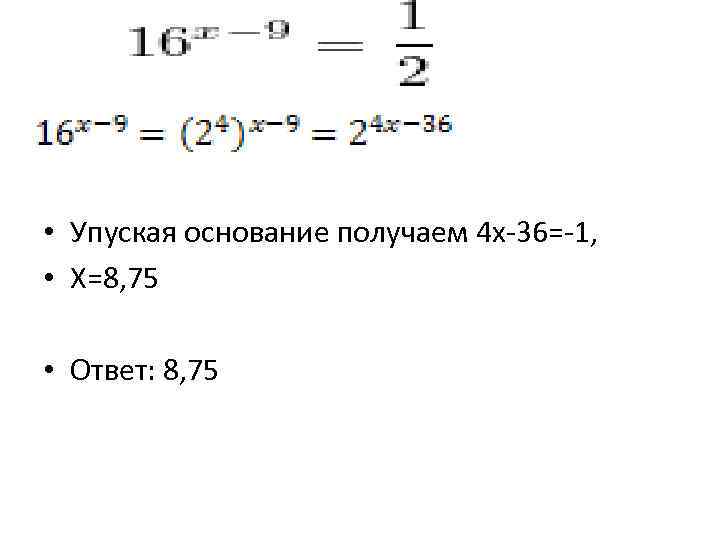• Упуская основание получаем 4 х-36=-1, • Х=8, 75 • Ответ: 8, 75