Решение обратной задачи – AVO -инверсия Основные

Решение обратной задачи – AVO -инверсия

Основные понятия акустической, упругой и совместной (одновременной) инверсии • Акустическая инверсия (псевдоакустический каротаж) – определение зависимости акустического импеданса среды от времени по сейсмотрассе отраженных волн при нормальном падении. • Упругая инверсия – определение зависимости упругого импеданса среды от времени по сейсмотрассе отраженных волн, полученной при угле падения, отличном от нормального. • Совместная инверсия – определение зависимости акустических импедансов продольных и поперечных волн и плотности среды от времени по сейсмограмме отраженных волн для различных углов падения

Что лежит в основе акустической инверсии? • 1. Сверточная модель сейсмограммы. 2. Выражение для коэффициента отражения при нормальном падении 3. Возможность получения значений импедансов из кривых коэффициентов отражения

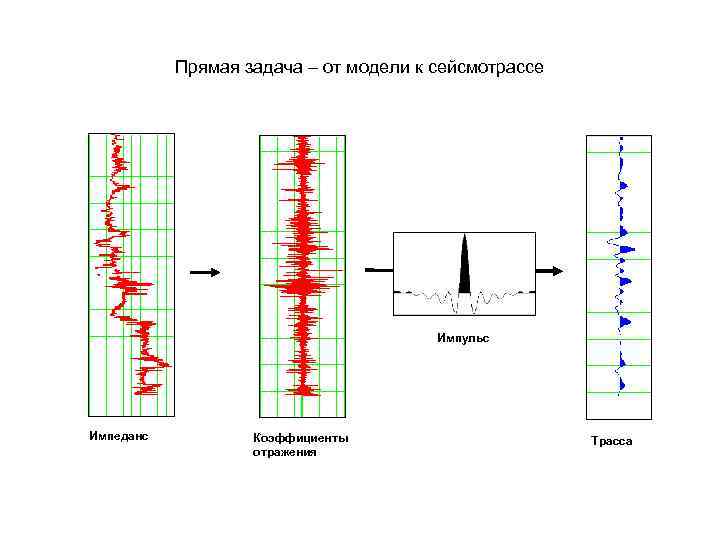
Прямая задача – от модели к сейсмотрассе Импульс Импеданс Коэффициенты отражения Трасса

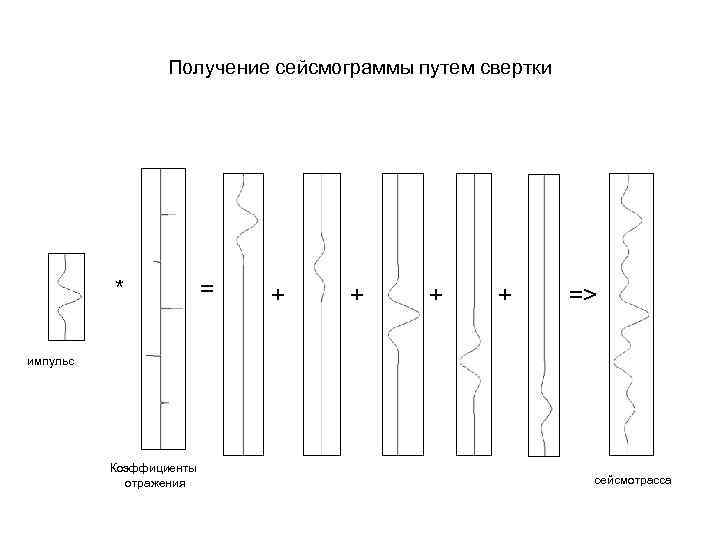
Получение сейсмограммы путем свертки * = + + => импульс Коэффициенты отражения сейсмотрасса

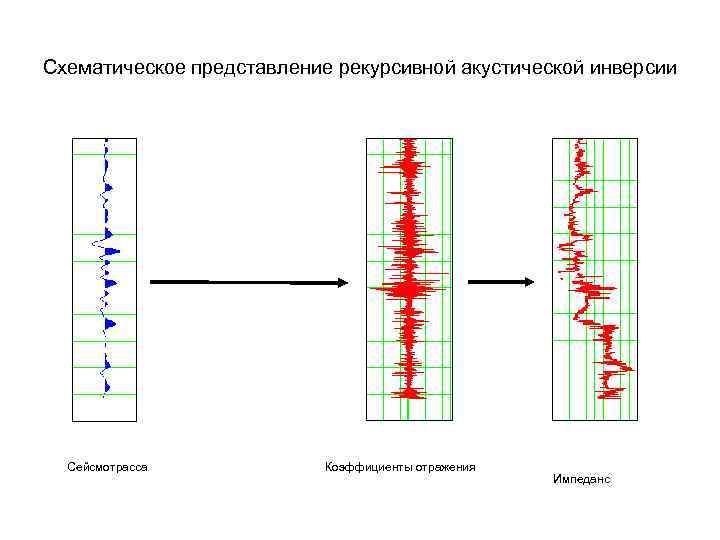
Схематическое представление рекурсивной акустической инверсии Сейсмотрасса Коэффициенты отражения Импеданс

• • • Физический смысл акустической инверсии предельно ясен: от коэффициентов отражения, которые характеризуют свойства границ, мы переходим к акустическим жесткостям, которые характеризуют собственно среду. Для этого необходимо максимально сжать сейсмический импульс – «избавиться от формы» . Несмотря на простоту исходных формул, процедура акустической инверсии далеко не однозначна. В оценку коэффициента отражения по сейсмотрассе обязательно входят неустраненные случайные и регулярные помехи, искажения формы сейсмического импульса, связанные с распространением в реальной среде. Акустическая инверсия в принципе может производиться только в том случае, когда для изучаемого интервала в районе исследований имеются данные акустического каротажа по нескольким скважинам.

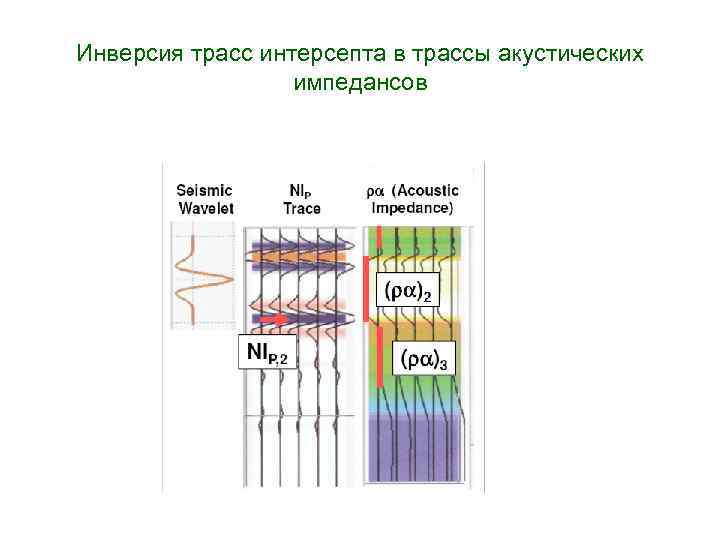
Инверсия трасс интерсепта в трассы акустических импедансов

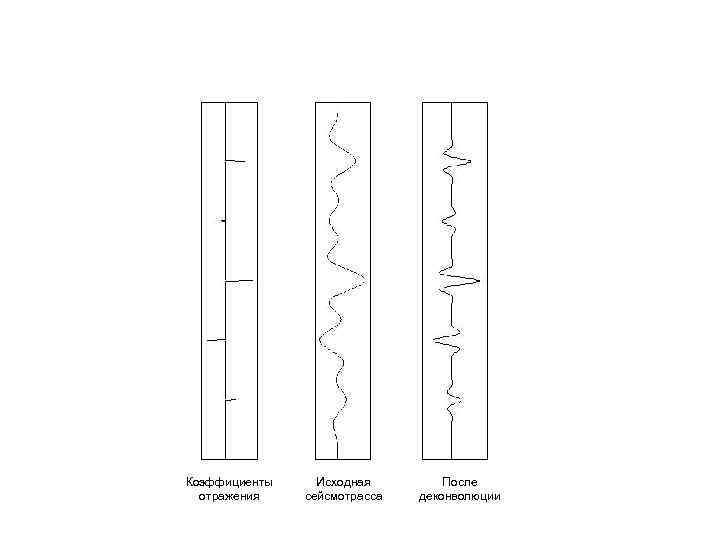
Коэффициенты отражения Исходная сейсмотрасса После деконволюции

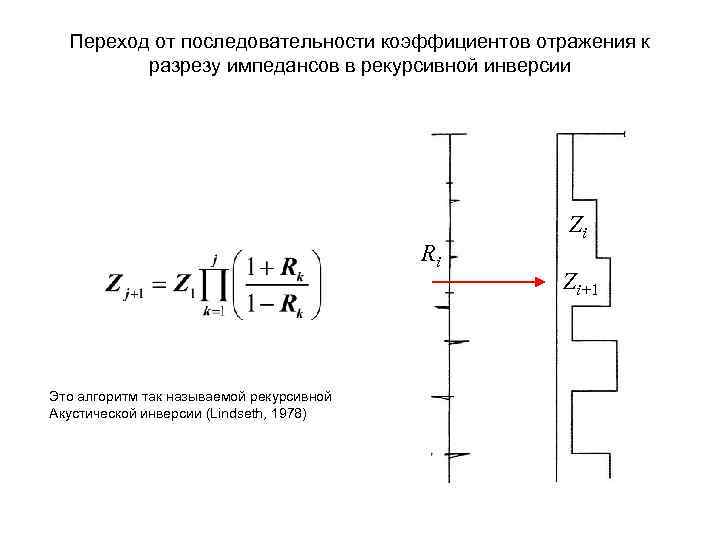
Переход от последовательности коэффициентов отражения к разрезу импедансов в рекурсивной инверсии Ri Это алгоритм так называемой рекурсивной Акустической инверсии (Lindseth, 1978) Zi Zi+1

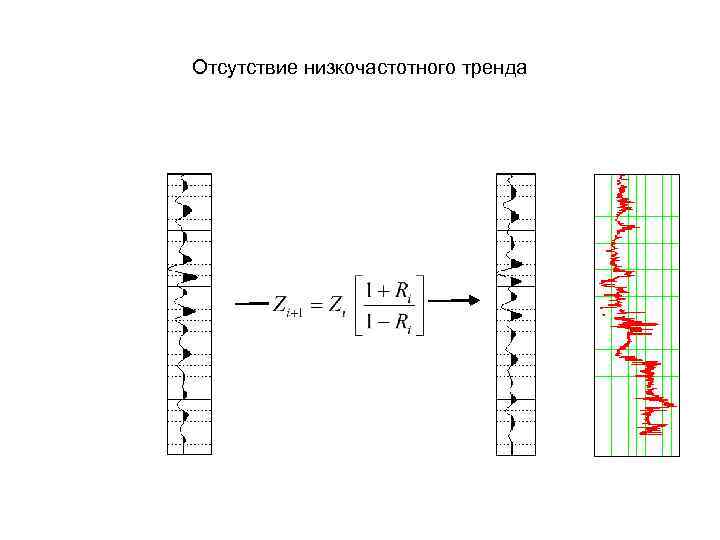
Отсутствие низкочастотного тренда

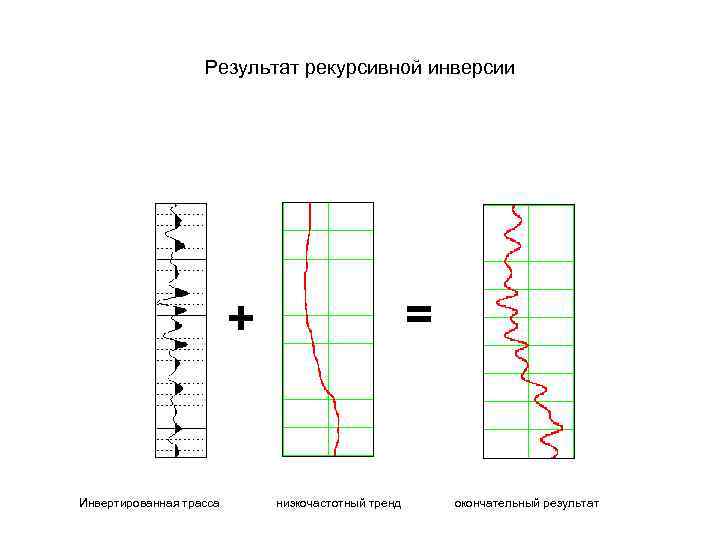
Результат рекурсивной инверсии = + Инвертированная трасса низкочастотный тренд окончательный результат

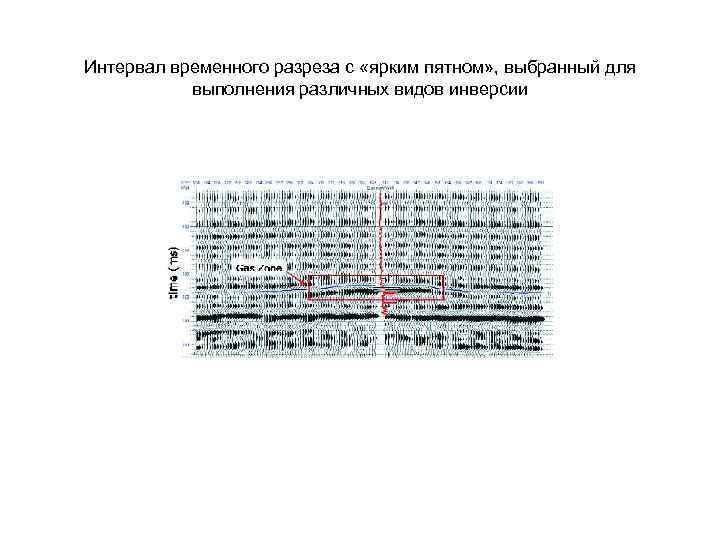
Интервал временного разреза с «ярким пятном» , выбранный для выполнения различных видов инверсии

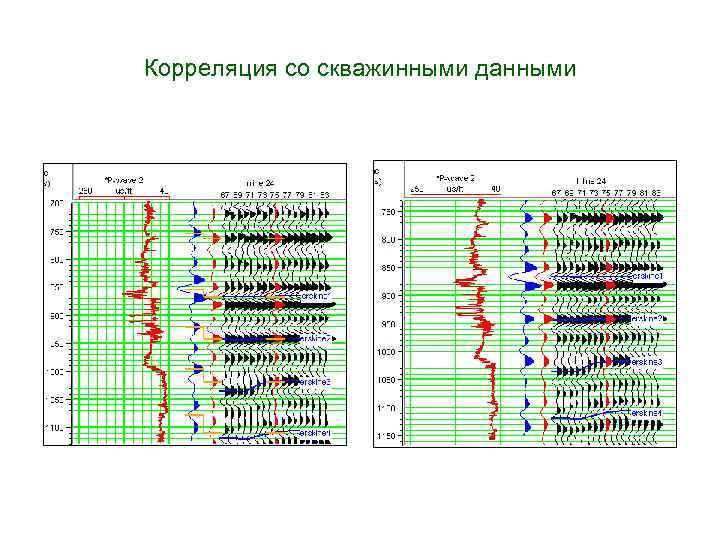
Корреляция со скважинными данными

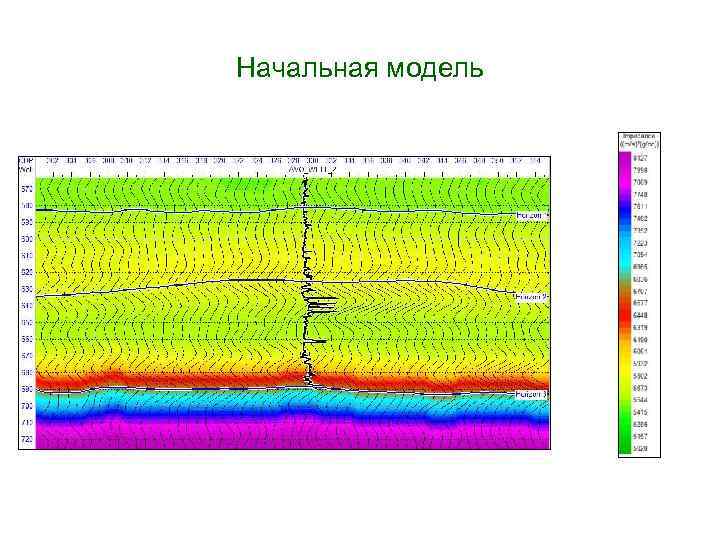
Начальная модель

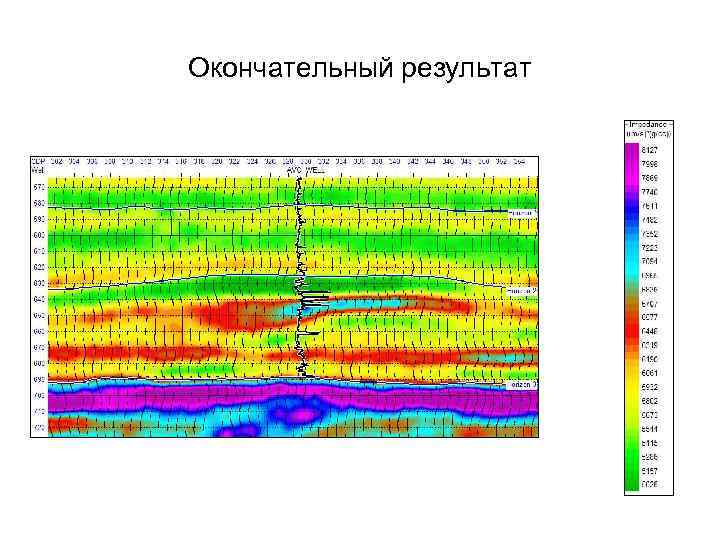
Окончательный результат

Ограничения рекурсивной инверсии • • • 1. Невозможно полностью «избавиться от формы импульса» - получить сейсмотрассу дельта-функций Есть определенный произвол в добавлении низкочастотной компоненты Суммотрасса – не точный аналог сейсмотрассы, полученной при нормальном падении

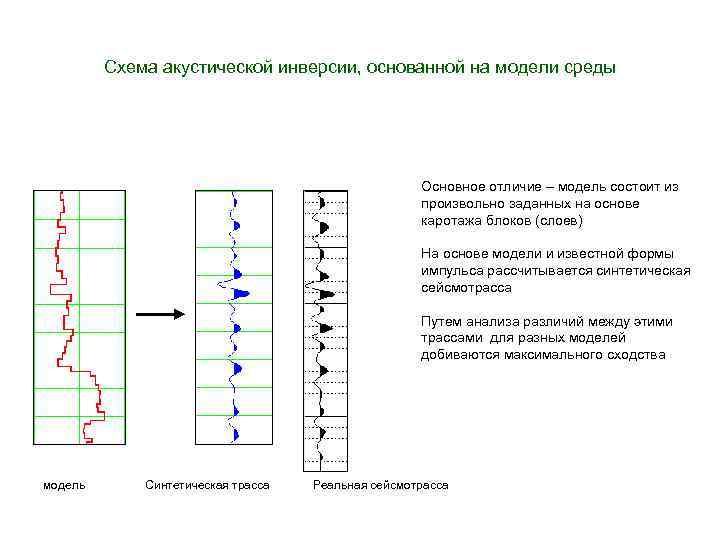
Схема акустической инверсии, основанной на модели среды Основное отличие – модель состоит из произвольно заданных на основе каротажа блоков (слоев) На основе модели и известной формы импульса рассчитывается синтетическая сейсмотрасса Путем анализа различий между этими трассами для разных моделей добиваются максимального сходства модель Синтетическая трасса Реальная сейсмотрасса

Базовый алгоритм акустической инверсии, основанной на начальной модели (model-based inversion) Имеется модель, состоящая из N слоев с мощностями hi, скоростями vi и плотностями ri Время пробега в i -ом слое ti. Время пробега до кровли i-ого слоя Сверточное представление трассы Здесь k – отсчет, на котором берется значение Т(к). Число уравнений равно числу отсчетов в сейсмотрассе Ns. Если Ns>N, система решается. Зададим начальную модель распределения коэффициентов отражения R 0 (j) Тогда можно рассчитать синтетическую сейсмотрассу

Реальная трасса отличается от синтетической по 2 причинам: R 0 отличается от R; реальная трасса содержит шум. Наша задача – свести к минимуму различия между реальной и синтетической трассами. Пусть Методом наименьших квадратов находим значения D r(j), для которых квадрат разностей синтетической и реальной трасс (целевая функция) станет минимальным.

Перейдем к матричным представлениям. Пусть трасса – вектор длиной Ns, последовательность неизвестных коэффициентов отражения – вектор длиной N, набор импульсов – матрица из N столбцов и Ns строк. Столбцы содержат импульс, сдвинутый на двойное время пробега для каждого слоя Ns = K + N -1, К – число дискретов в импульсе Тогда синтетическую сейсмотрассу можно записать в виде произведения векторов, Вектор ошибки

Целевая функция в матричном виде имеет вид: Решение получаем приравниванием производных от J по каждому элементу вектора R к 0 Получаем систему из N нормальных уравнений с N неизвестными Полное решение имеет вид:

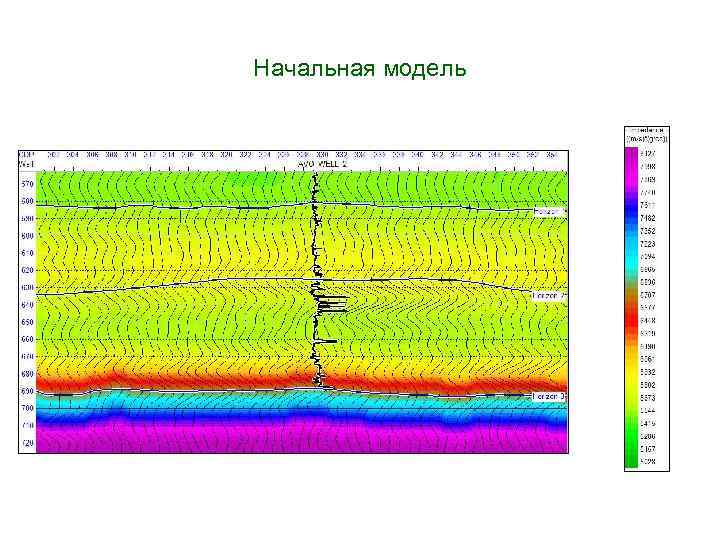
Начальная модель

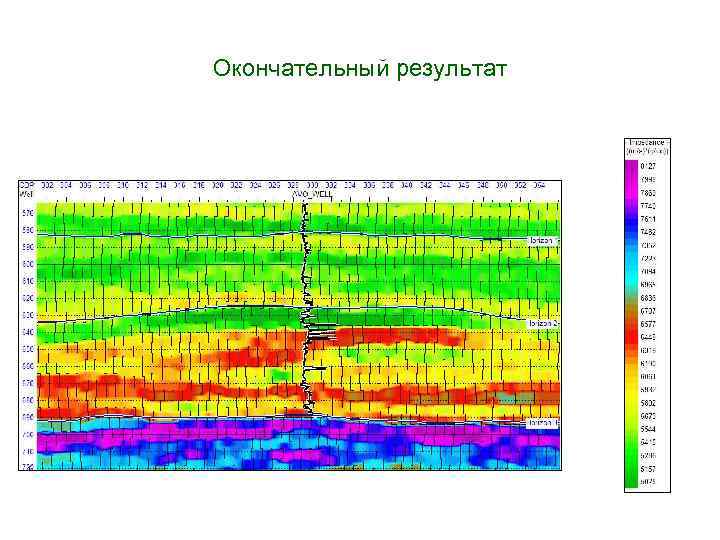
Окончательный результат

Сопоставление результатов рекурсивной и основанной на модели инверсии

Акустическая инверсия в логарифмическом приближении для малых коэффициентов отражения Пусть модель состоит из m+1 слоя Существуют m коэффициентов отражения (вектор длиной m)

В матричном виде коэффициент отражения Матрица D содержит m+1 столбцов и m строк. Учитывая, что трасса представляет собой свертку импульса и последовательности коэффициентов отражений, будем искать вектор L, который обеспечит минимум целевой функции Теперь неизвестные – это логарифмы импедансов, а не коэффициенты отражения. Должны быть заданы нижние и верхние границы импедансов. Для решения используется метод сопряженных градиентов с ограничениями

Наиболее распространенные алгоритмы АИ 1. Инверсия редких импульсов с ограничениями – CSSI (Constrained Sparse Spike Inversion) Основана на сверточной модели сейсмотрассы и на горизонтально-слоистой модели, состоящей из мощных однородных пластов. Сумма модулей коэффициентов отражения, формирующих сейсмотрассу, должна быть минимальна. Необходима низкочастотная модель. Импульс должне быть близким к нуль-фазовому. 2. Геостатистическая инверсия - вероятностная. На основе скважинных данных и вариограмм, задающих распределение свойств среды, создаются множественные реализации моделей. подбираются наиболее вероятные реализации, обеспечивающие наименьшую невязку между модельными и наблюденными сейсмотрассами.

Принципиальные трудности применения АИ. • В основе АИ лежит уравнение, из которого следует, что нам необходимо найти абсолютные значения импеданса по его относительным приращениям. Понятно, что эта задача может решаться только в том случае, когда имеется некоторое начальное абсолютное значение. • На практике в сейсмическом диапазоне частот, во-первых, невозможно выделить отражения от пластов, мощность которых меньше ¼ длины волны, вовторых, мы не можем зарегистрировать отражений от низкочастотной составляющей кривой импеданса (частоты ниже содержащихся в спектре сейсмического импульса). Низкочастотные и высокочастотные компоненты импеданса приходится получать из других данных: акустического и плотностного каротажа. Низкочастотную компоненту получают из миграционной модели. Необходимо хорошее знание формы импульса Амплитуды волн на суммотрассах не всегда точно отражают соотношение между импедансами • •

Общая схема решения задачи АИ. В различных системах обработки и интерпретации существуют различные версии акустической инверсии. Во всех присутствуют 4 основных этапа. • • • 1. Создание сейсмоакустической модели изучаемого интервала разреза для каждой из имеющихся скважин с АК. Интервал должен быть ограничен опорными сейсмическими горизонтами. На этом этапе производится согласование скоростных кривых АК с данными сейсморазведки. Для этого выполняются следующие процедуры: а) преобразование кривых АК во временной масштаб и их изменение в пределах возможных погрешностей АК (сжатие, растяжение) с целью наилучшего согласования синтетических и реальных сейсмотрасс. 2) сглаживание кривых АК или разбиение их на «блоки» с целью перехода от дискретизации в сантиметры к дискретизации в метры или десятки метров. 3) оценка формы сейсмического импульса, расчет амплитудного и фазового спектров; 4) расчет синтетических сейсмотрасс и сопоставление с ними реальных сейсмотрасс. При этом путем последовательного изменения модели добиваются, чтобы коэффициент взаимной корреляции синтетики и полевой трассы достиг заданного порогового значения. Подобранная в результате «ступенчатая» кривая АК и выбранная форма импульса являются эффективной сейсмоакустической моделью СМ для участка данной скважины.

Преобразование кривых АК во временном масштабе

2. Создание для всей изучаемой площади априорной геоакустической модели ( «фоновой модели» . Обозначим ее ФМ. Для этого выполняется интерполяция и экстраполяция СМ на всю площадь, при этом а) используются только данные АК; б) модель является однородно-слоистой по каждой скважине, мощность слоев задается произвольно и должна лежать в пределах от минимальной разрешающей способности по вертикали, установленной по сейсмическим данным, до вертикальной разрешенности АК. в) интерполяция между скважинами выполняется с учетом геометрии сейсмических границ. Другими словами, верхняя и нижняя граница фоновой модели задаются, исходя из геометрии кровли и подошвы изучаемого интервала, а внутри этого интервала его строение задается данными АК, разбитыми на слои с «разумной» вертикальной разрешенностью. Свойства же самих этих слоев между скважинами интерполируются линейно, тогда как их границы между скважинами должны вести себя в соответствии с сейсмическими данными. Таким образом, фоновая модель имеет горизонтальную разрешенность сейсмики, а вертикальную – почти как у АК.

• • 3. Построение разрезов акустического импеданса. Здесь выполняется обращение уравнения и дополнение результата обращения высокими и низкими частотами. При этом геометрия интервала практически не меняется, а строение интервала (его свойства) объединяет сейсмические и ГИСовские данные. Итогом является модель импедансов (ИМ). 4. От модели ИM с помощью статистических связей можно перейти к модели пространственных вариаций коллекторских свойств, чаще всего, пористости, иногда – проницаемости.

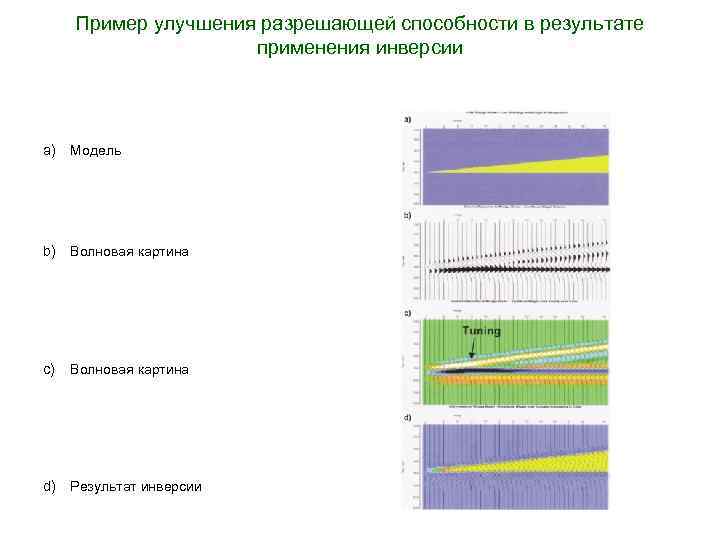
Пример улучшения разрешающей способности в результате применения инверсии a) Модель b) Волновая картина c) Волновая картина d) Результат инверсии

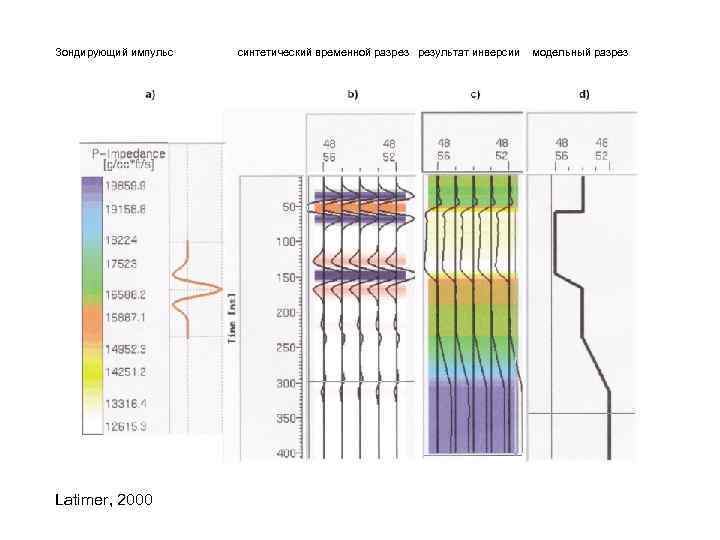
Зондирующий импульс Latimer, 2000 синтетический временной разрез результат инверсии модельный разрез

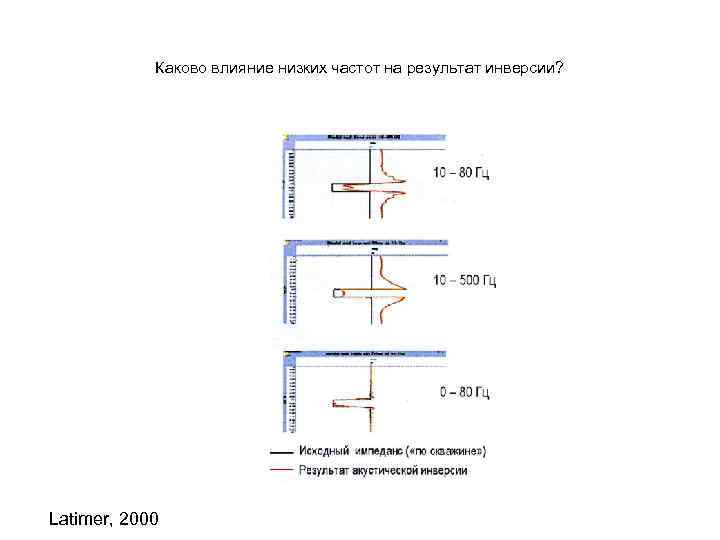
Каково влияние низких частот на результат инверсии? Latimer, 2000

Упругая (эластическая) инверсия • Акустическая инверсия выполняется для сейсмотрасс, полученных при отражении при нормальном падении волн на границы, следовательно, в ней могут рассматриваться только монотипные (практически всегда) продольные волны. • При наклонном падении в коэффициенте отражения содержится информация не только об акустическом импедансе, но и о скорости распространения поперечной волны. Резонным представляется вопрос: нельзя ли применить инверсию типа акустической к трассам, полученным под ненулевыми углами падения? В этом случае речь может идти об «упругой» инверсии, при этом имеется в виду, что при акустической инверсии мы как бы восстанавливаем акустическую среду, в которой распространяются только продольные волны, а при упругой – упругую, в которой распространяются волны обоих типов. Эта идея возникла еще в начале 90 -х гг. , но решение было опубликовано только в конце 90 -х.

Теория упругого импеданса Метод упругих импедансов (EI) был предложен Патриком Конноли в 1999 году ( Connolly, 1999). По аналогии с выражением для коэффициента отражения при нормальном падении где AI – акустический импеданс или акустическая жесткость, равный произведению плотности на скорость распространения продольных волн, он предложил выразить коэффициент отражения для произвольного угла падения через упругие импедансы EI. Учитывая, что - константа

преобразуем уравнение Аки- Ричардса к виду:

Отсюда можно получить выражение для EI: При нормальном падении выражение для упругого импеданса совпадает с выражением для акустического импеданса. Однако размерность упругого импеданса в данном случае зависит от угла падения. В работе Ver. West B. , 2000 приводится другое выражение для EI. Функция Ф в данном выражении не раскрывается авторами, указывается только, что с ее помощью размерность упругого импеданса приводится к размерности акустического.

• Очевидно, что если определить упругий импеданс как минимум для трех различных углов падения, можно найти три неизвестных величины – VP, VS и ρ. С другой стороны, можно применять для упругой инверсии весь уже разработанный аппарат акустической инверсии, но результатом будут три фоновые геоакустические модели – по каждому из упругих параметров. • В основе вывода понятия упругого импеданса лежит та же аппроксимация Аки-Ричардса, что и для вывода основных параметров AVO – градиента и интерсепта. Очевидно, что упругий и акустический импеданс должны реагировать на нефте-газонасыщение аналогично тому, как реагируют на них интерсепт и градиент. Поскольку наиболее чувствителен к характеру флюидонасыщения именно градиент, можно ожидать того, что и упругий импеданс будет вести себя аналогично градиенту АVO. Основное преимущество упругой инверсии по сравнению с AVOанализом – не требуется предположение о постоянстве формы импульса для всех удалений. Для каждой частичной угловой суммы определяется свой импульс. •

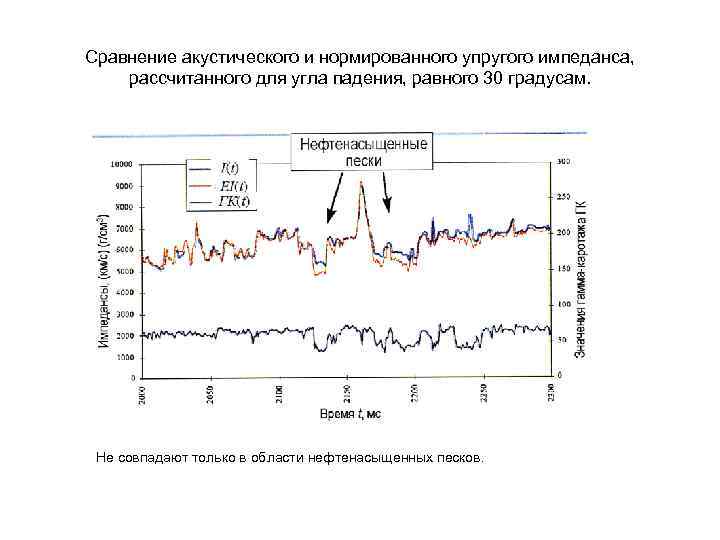
Сравнение акустического и нормированного упругого импеданса, рассчитанного для угла падения, равного 30 градусам. Не совпадают только в области нефтенасыщенных песков.

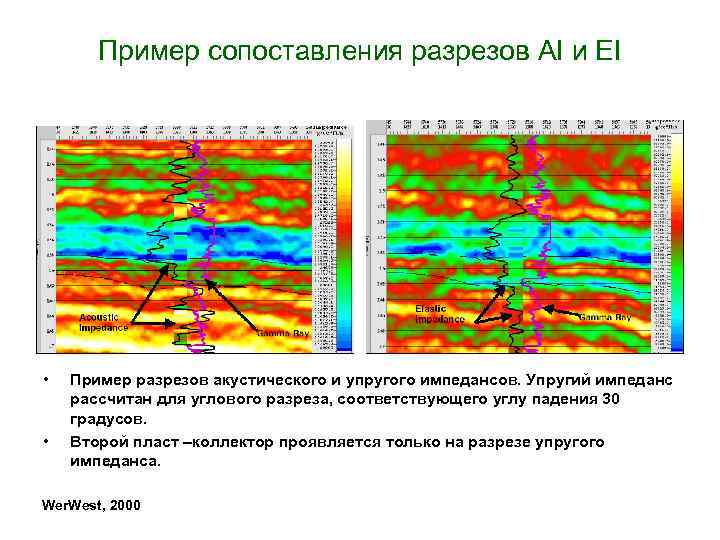
Пример сопоставления разрезов AI и EI • • Пример разрезов акустического и упругого импедансов. Упругий импеданс рассчитан для углового разреза, соответствующего углу падения 30 градусов. Второй пласт –коллектор проявляется только на разрезе упругого импеданса. Wer. West, 2000

Продолженный (расширенный) упругий импеданс EEI. В работе [Whitcombe, 2002] было предложено: 1) использовать двучленную аппроксимацию, приняв, что f = C/R 0 - константа. 2) Продолжить прямую, соответствующую двучленной аппроксимации, влево и вправо от области, где верна эта аппроксимация 3) Заменить sin 2 q на tg X, при этом -90<Х < 90. Экстраполированная прямая R(sin 2 q) Смысл этого действия: рассчитывая EEI в различных диапазонах углов, можно получать аналоги разрезов различных упругих модулей Whitcombe, 2002

Получены связи между упругими свойствами среды, такими как: объемный модуль К, параметры Ламе, модуль сдвига, скорости распространения волн – и АVO-параметрами: интерсептом, градиентом и величиной f. Связь с углом падения в явном виде отсутствует. Надо перейти к привычному «двучленному» виду. Примем g = 0. 25 , f = 0. 8:

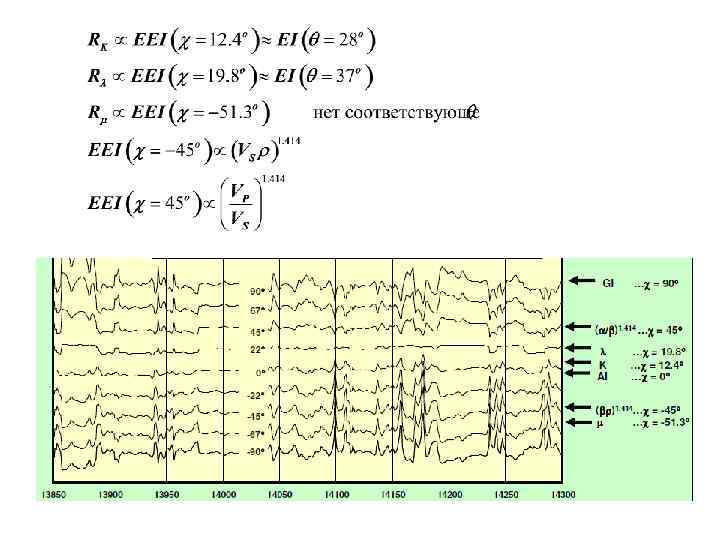
• Теперь уравнение нормированного упругого импеданса примет вид: VP, 0, ρ0 - константы, соответствующие средним значениям, выбранным по ГИС При = 0 расширенный импеданс становится просто акустическим импедансом I, при = 90 – так называемым градиентным импедансом GI. Тогда EEI можно выразить через акустический и градиентный импеданс:

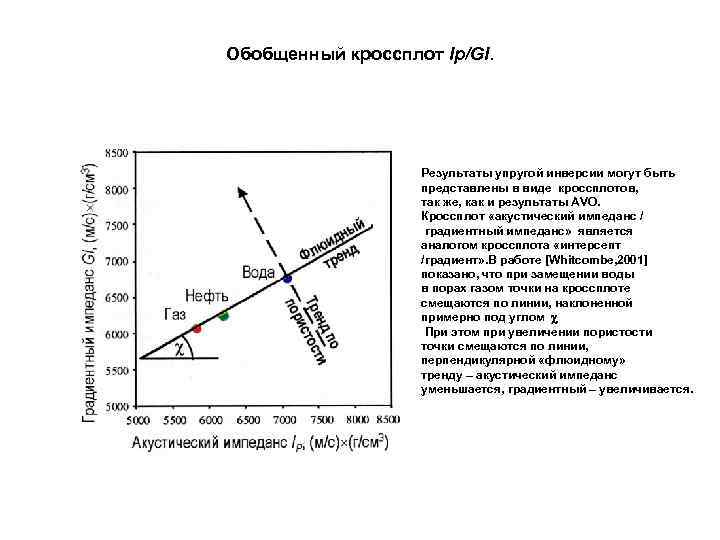
Обобщенный кроссплот Ip/GI. Результаты упругой инверсии могут быть представлены в виде кроссплотов, так же, как и результаты AVO. Кроссплот «акустический импеданс / градиентный импеданс» является аналогом кроссплота «интерсепт /градиент» . В работе [Whitcombe, 2001] показано, что при замещении воды в порах газом точки на кроссплоте смещаются по линии, наклоненной примерно под углом При этом при увеличении пористости точки смещаются по линии, перпендикулярной «флюидному» тренду – акустический импеданс уменьшается, градиентный – увеличивается.

Пример разделения чистых продуктивных и заглинизированных непродуктивных песков с помощью EEI Саудовская Аравия. а) кроссплот глинистости и акустического импеданса; б) кроссплот глинистости и упругого импеданса: с) сопоставление кривых глинистости и продолженного упругого импеданса. Чистые песчаники с малыми значениями ГК (красные крестики) не отличаются от глинизированных (синие кружочки) по значениям акустического импеданса, но отличаются по значениям упругого импеданса.

Упругая инверсия • • • Выполняется аналогично акустической инверсии, но для ненулевых удалений Идеальная частичная угловая сумма – набор амплитуд, относящихся к выбранному узкому диапазону углов падения в пределах большого временного окна – последовательность коэффициентов отражения для ограниченного углового диапазона. Существуют два способа конструирования частичных угловых сумм. В основе первого лежит определение углов падения и построение сейсмограмм равных углов. В основе второго – расчет и применение функций внешнего и внутреннего мьютинга, при этом не обнуляются и суммируются только узкие области внутри выбранного углового диапазона

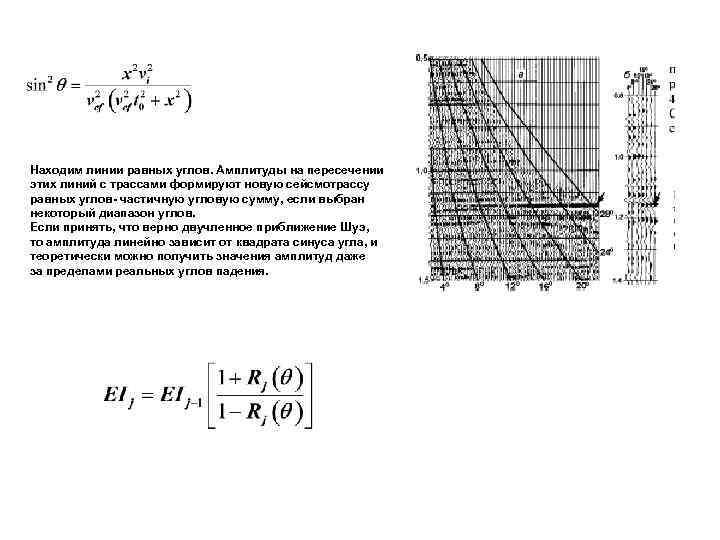
Находим линии равных углов. Амплитуды на пересечении этих линий с трассами формируют новую сейсмотрассу равных углов- частичную угловую сумму, если выбран некоторый диапазон углов. Если принять, что верно двучленное приближение Шуэ, то амплитуда линейно зависит от квадрата синуса угла, и теоретически можно получить значения амплитуд даже за пределами реальных углов падения.

Особенности упругой инверсии • • Существенным преимуществом упругой инверсии по сравнению с традиционным AVO анализом является тот факт, что в ней форма импульса должна определяться для каждой частичной угловой суммы, являющейся аналогом сейсмотрассы нормального падения в акустической инверсии. В обычном же AVO принято считать форму импульса неизменной для всех углов падения, что вызывает существенные ошибки. Общей проблемой как для AVO , так и для упругой инверсии, является зависимость от величины отношения VS / VP. Это отношение может меняться по разрезу, но мы должны считать его постоянным. Погрешность оценки коэффициента отражения за счет отклонения величины от заданной выражается [Connolly] Процедура упругой инверсии обладает меньшей помехоустойчивостью, чем акустическая инверсия. Это связано с тем, что для акустической инверсии используется суммотрасса, полученная суммированием трасс, соответствующим всем имеющимся углам падения. Для упругой инверсии необходимо в идеале использовать одну трассу, соответствующую конкретному углу падения, но в действительности используются частичные угловые суммы. Однако соотношение сигнал/помеха для них будет существенно ниже, чем для суммы по всем углам.

Пример успешного использования метода упругих импедансов В работе G. Cambois, (2000) рассмотрен убедительный пример достоинств метода упругих импедансов по сравнению с стандартным AVO-анализом в условиях, когда имеет место большая изменчивость формы импульса с расстоянием. Приведены три угловых разреза-ближний, средний и дальний. Очевидная амплитудная аномалия. Но возможна ли количественная оценка AVO-параметров? G. Cambois, 2000

а) б) в) А) каротажные кривые : красная – Vs, синяя –Vp, зеленая – плотность, черная – акустический импеданс, который практически не меняется в коллекторе. Б) синтетические сейсмограммы. Хорошо видно изменение формы сигнала. В) на кривой (Vs/ Vp) 2 ( справа) виден отчетливый скачок. G. Cambois, 2000

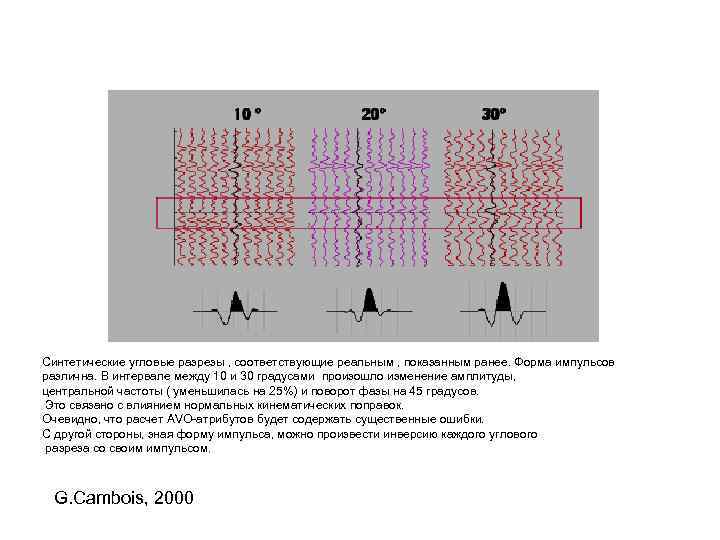
Синтетические угловые разрезы , соответствующие реальным , показанным ранее. Форма импульсов различна. В интервале между 10 и 30 градусами произошло изменение амплитуды, центральной частоты ( уменьшилась на 25%) и поворот фазы на 45 градусов. Это связано с влиянием нормальных кинематических поправок. Очевидно, что расчет AVO-атрибутов будет содержать существенные ошибки. C другой стороны, зная форму импульса, можно произвести инверсию каждого углового разреза со своим импульсом. G. Cambois, 2000

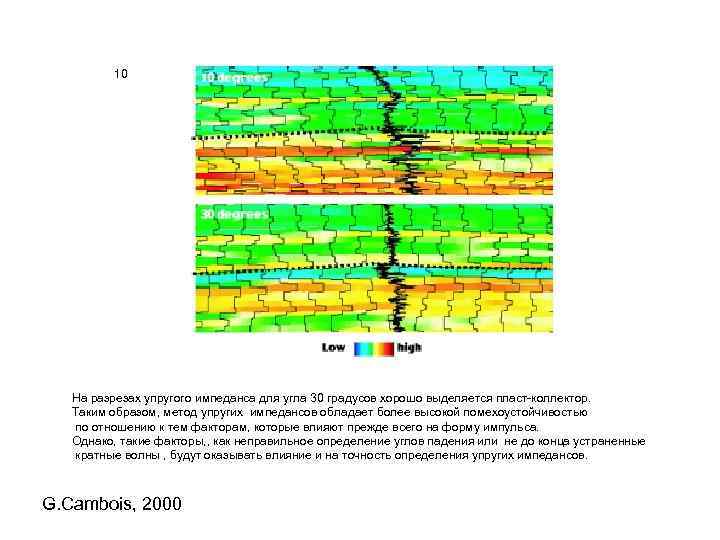
10 На разрезах упругого импеданса для угла 30 градусов хорошо выделяется пласт-коллектор. Таким образом, метод упругих импедансов обладает более высокой помехоустойчивостью по отношению к тем факторам, которые влияют прежде всего на форму импульса. Однако, такие факторы, , как неправильное определение углов падения или не до конца устраненные кратные волны , будут оказывать влияние и на точность определения упругих импедансов. G. Cambois, 2000

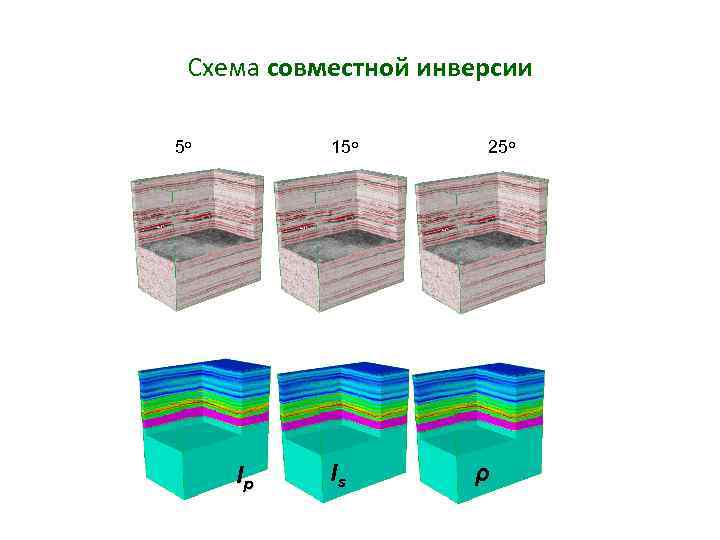
Схема совместной инверсии 5 о 15 о Ip Is 25 о ρ

Теория комплексного (совместного) обращения (simultaneous inversion) Цель совместной инверсии: инвертировать сейсмограммы ОГТ до суммирования в разрезы акустических импедансов Zp, Zs и плотности r. Обратимся к аппроксимации Fatti (1994). Fatti преобразовал уравнение Аки-Ричардса к виду:

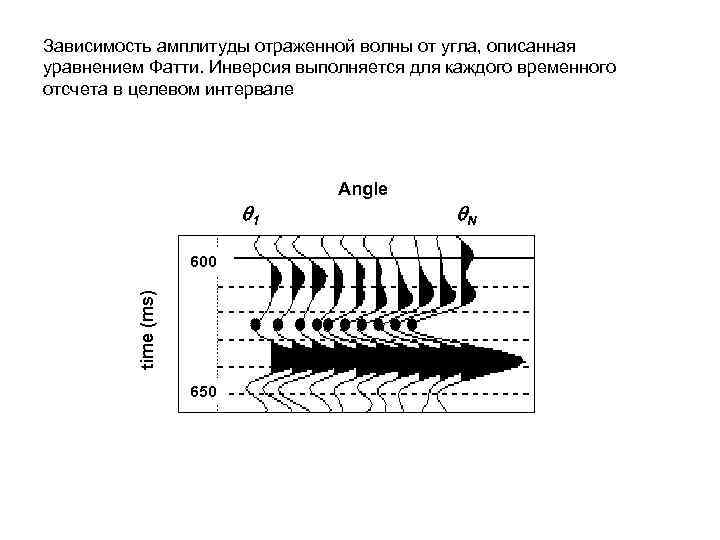
Зависимость амплитуды отраженной волны от угла, описанная уравнением Фатти. Инверсия выполняется для каждого временного отсчета в целевом интервале q 1 time (ms) 600 650 Angle q. N

Примеры сейсмограмм ОГТ, сформировавших выделенный прямоугольником интервал временного разреза

Последовательность действий при совместной инверсии 1. На основе каротажных и сейсмических данных строится модель Р-импедансов; 2. Выполняется извлечение формы сейсмического импульса для каждого выбранного угла. 3. Находят взаимосвязи между скоростью продольных волн, скоростью поперечных волн и плотностью. Затем выполняется инверсия методом сопряженных градиентов.

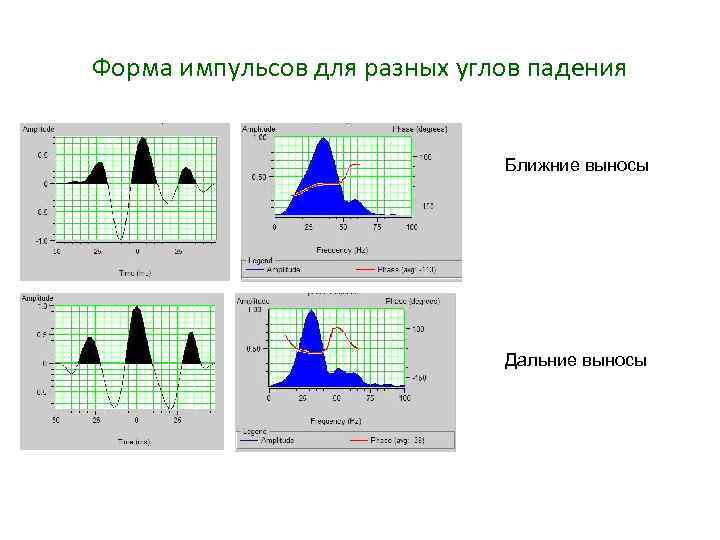
Форма импульсов для разных углов падения Ближние выносы Дальние выносы

Для упрощения принято использовать приближение для малых коэффициентов отражения

В матричном виде для N трасс получим

Нам необходимо учесть тот факт, что сейсмотрасса состоит из импульсов, имеющих ограниченную полосу частот. Введем матричное представление сейсмотрассы, обозначив через W импульс, формирующий сейсмотрассу Теперь уравнение Fatti будет выглядеть так Заметим, что форма импульса в общем случае может быть различна для разных углов падения.

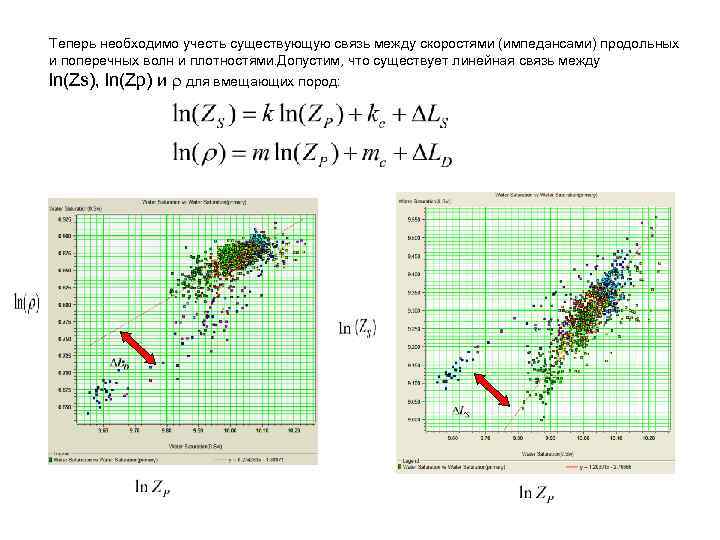
Теперь необходимо учесть существующую связь между скоростями (импедансами) продольных и поперечных волн и плотностями. Допустим, что существует линейная связь между ln(Zs), ln(Zp) и r для вмещающих пород:

Тогда уравнение Фатти приобретет новый вид: Пусть имеется N сейсмотрасс, соответствующих N углам падения и, соответственно, N значений амплитуд на фиксированном времени для этих углов. В матричном виде они запишутся так:

Тогда примерный алгоритм инверсии может выглядеть так: 1)Исходная информация: - набор N сейсмотрасс, соответствующих N углам падения - набор N форм импульсов для каждого угла - начальные значения акустических импедансов и плотности 2) По скважинным данным рассчитываются оптимальные значения коэффициентов k m 3) Устанавливаются начальные условия: 4) Система уравнений решается методом сопряженных градиентов. 5) Рассчитываются окончательные значения импедансов и плотности

Что лежит в основе предложенного алгоритма инверсии? • • • 1. Трехчленная аппроксимация Аки-Ричардса, преобразованная Фатти 2. Предположение о небольших коэффициентах отражения 3. Предположение о линейной связи между ln(Zs), ln(Zp) и r 4. Предположение о постоянстве соотношения Vs/Vp 5. Искажения, вносимые в сейсмотрассу при вводе кинематической поправки, учитываются заданием формы импульса для каждого угла падения

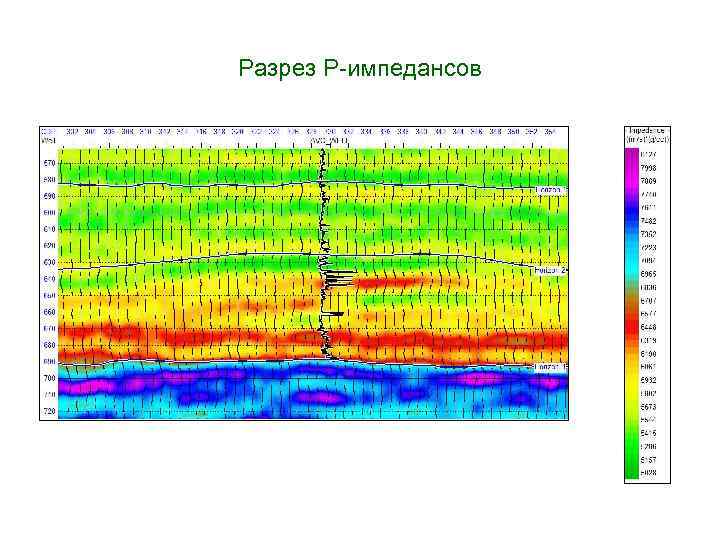
Разрез Р-импедансов

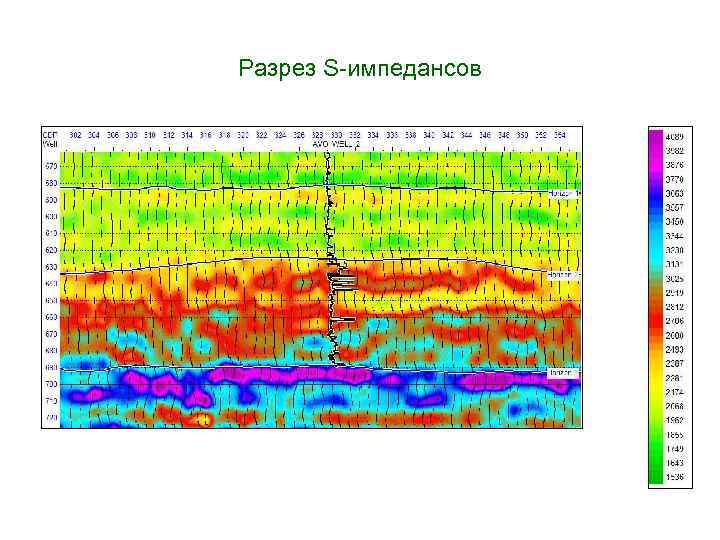
Разрез S-импедансов

Разрез плотности

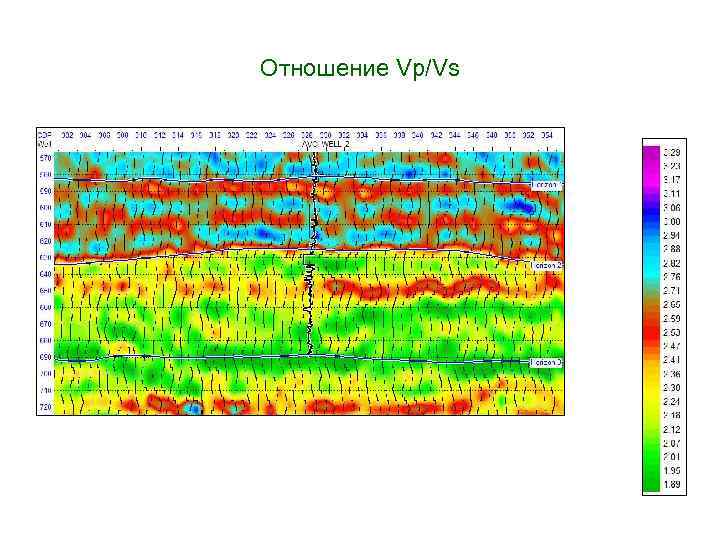
Отношение Vp/Vs

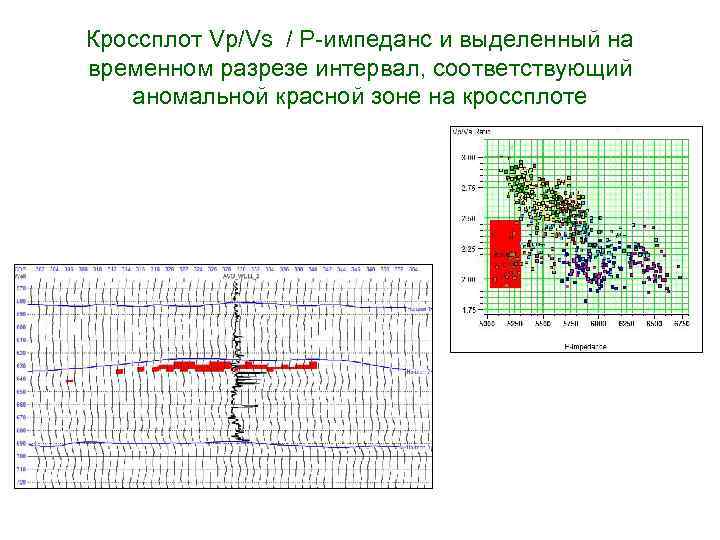
Кроссплот Vp/Vs / Р-импеданс и выделенный на временном разрезе интервал, соответствующий аномальной красной зоне на кроссплоте

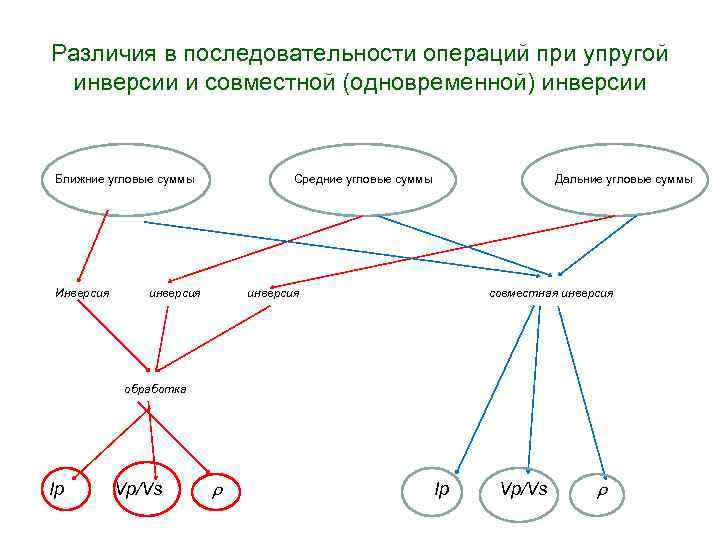
Различия в последовательности операций при упругой инверсии и совместной (одновременной) инверсии Ближние угловые суммы Инверсия Средние угловые суммы инверсия Дальние угловые суммы инверсия совместная инверсия обработка Ip Vp/Vs r

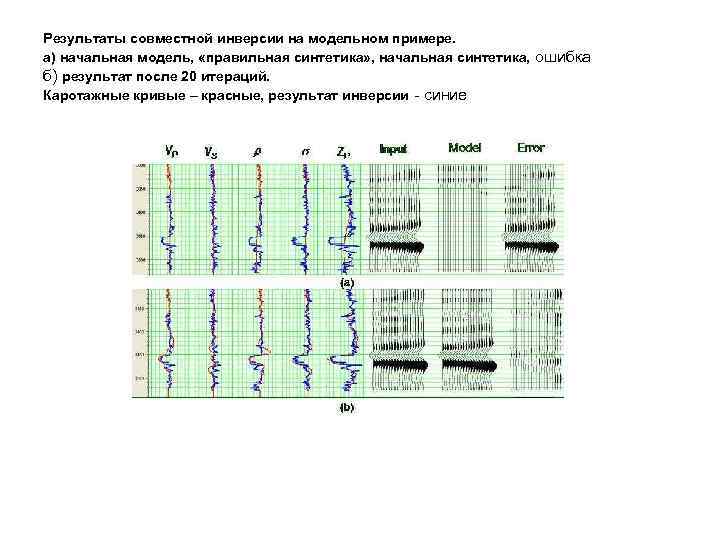
Результаты совместной инверсии на модельном примере. а) начальная модель, «правильная синтетика» , начальная синтетика, ошибка б) результат после 20 итераций. Каротажные кривые – красные, результат инверсии - синие

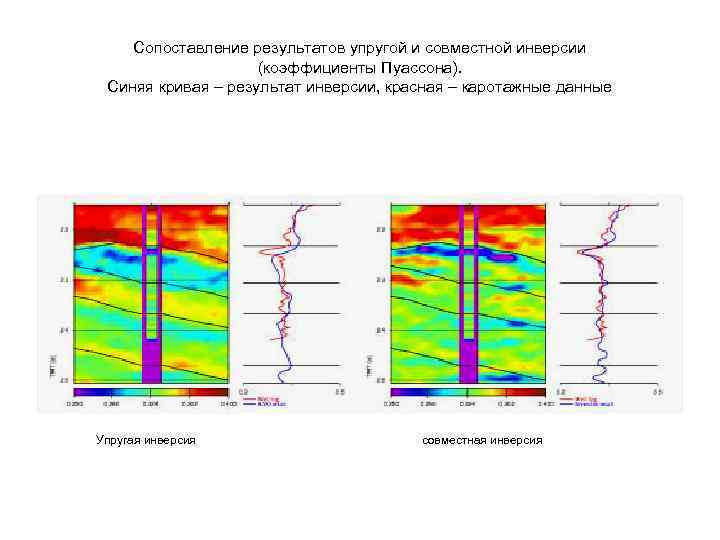
Сопоставление результатов упругой и совместной инверсии (коэффициенты Пуассона). Синяя кривая – результат инверсии, красная – каротажные данные Упругая инверсия совместная инверсия

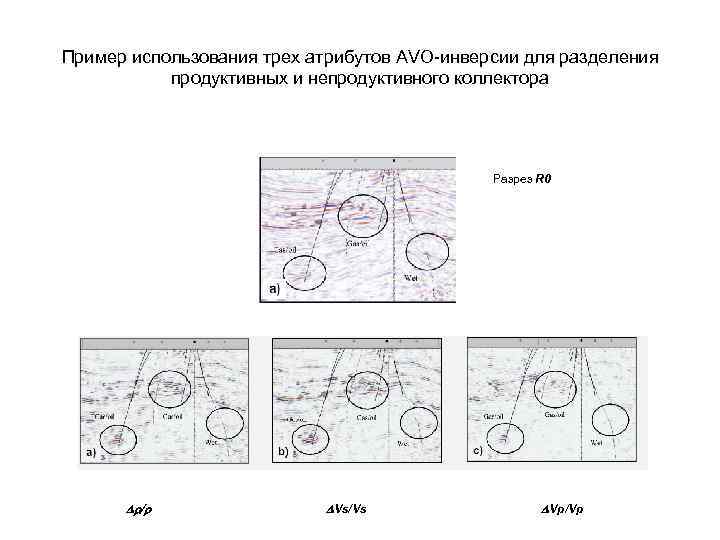
Пример использования трех атрибутов AVO-инверсии для разделения продуктивных и непродуктивного коллектора Разрез R 0 Dr/r DVs/Vs DVp/Vp

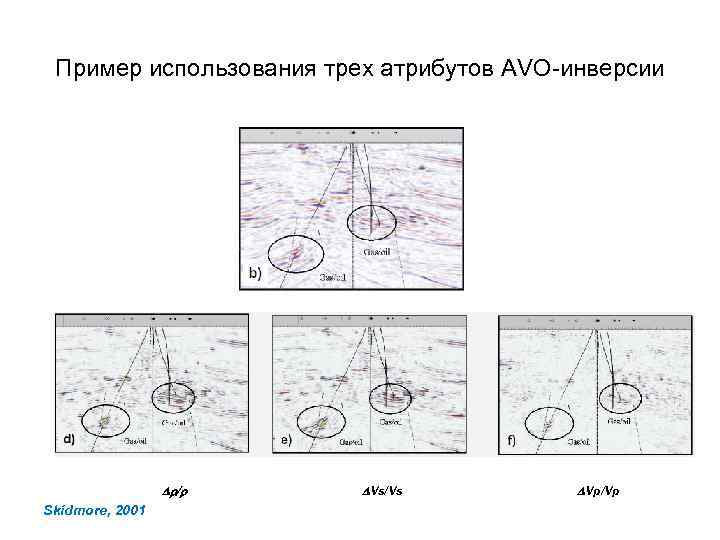
Пример использования трех атрибутов AVO-инверсии Dr/r Skidmore, 2001 DVs/Vs DVp/Vp