Решение игр mхn Эквивалентные задачи линейного программирования

Решение игр mхn. Эквивалентные задачи линейного программирования

Пусть имеется матричная игра mxn без седловой точки с матрицей выигрышей ||aij||. В соответствии с основной теоремой матричных игр, если платежная матрица не имеет седловой точки, то имеется пара оптимальных смешанных стратегий SA=||p 1, p 2, . . . , pm|| и SB=||q 1, q 2, . . . , qn||, применение которой обеспечивает игрокам получение цены игры Найдем SA. Предположим, что игрок В отказался от своей оптимальной смешанной стратегии SB и применяет только чистые стратегии. В каждом из этих случаев выигрыш игрока А будет не меньше, чем.

Разделив левую и правую часть каждого из неравенств на положительную величину v и введя обозначения: p 1+p 2+. . . +pm=1

min L(x)=x 1+x 2+. . . +xm.

Из решения задачи линейного программирования находим цену игры и оптимальную стратегию Sa по формулам:

Аналогично находим оптимальную стратегию SВ игрока В.

, max L(y)=y 1+y 2+. . . +ym. Эта задача является двойственной по отношению к задаче игрока А Оптимальная стратегия SB=||q 1, q 2, . . . , qn|| игрока В Таким образом, оптимальные стратегии SA=||p 1, p 2, . . . , pm|| и SB=||q 1, q 2, . . . , qn|| матричной игры mxn с платежной матрицей ||aij|| могут быть найдены путем решения пары двойственных задач линейного программирования:

Прямая (исходная) задача При этом . Двойственная задача

Пример. Найти решение и цену матричной игры, платежная матрица которой имеет вид Ai Bj B 1 B 2 B 3 A 1 1 2 3 A 2 3 1 1 A 3 1

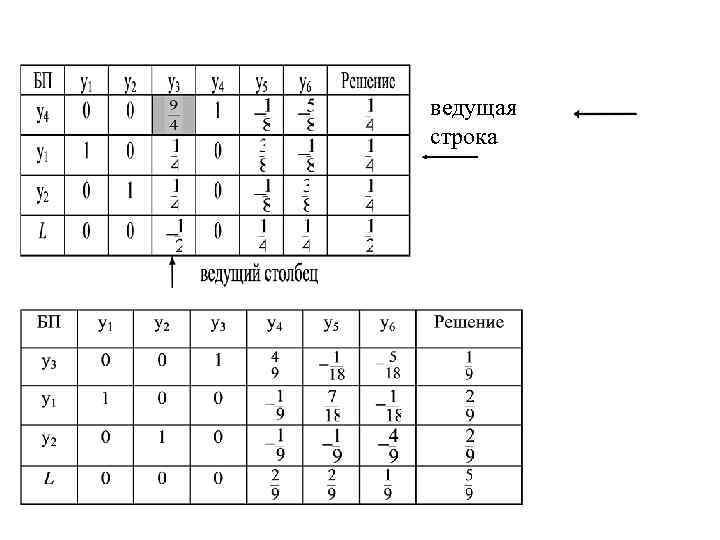ведущая строка

Находим оптимальную смешанную стратегию игрока В в соответствии с формулами

Оптимальное решение исходной задачи находим, используя двойственные оценки, из симплекс - таблицы для оптимального решения двойственной задачи: коэффициент при начальной базисной переменной в оптимальном уравнении прямой задачи равен разности между правой и левой частями ограничения двойственной задачи, ассоциированного с данной начальной переменной.

БЕСКОНЕЧНЫЕ АНТАГОНИСТИЧЕСКИЕ ИГРЫ