Решение геометрических задач повышенного уровня сложности методом координат

Решение геометрических задач повышенного уровня сложности методом координат

…Геометрия – это просто алгебра, воплощенная в фигурах. Софи Жермен (1776 -1831) q Выбираем в пространстве систему координат из соображений удобства выражения координат и наглядности изображения. q Находим координаты необходимых для нас точек. q Решаем задачу, используя основные задачи метода координат. q Переходим№ 01/2013 аналитических соотношений к от Журнал «Математика» геометрическим.

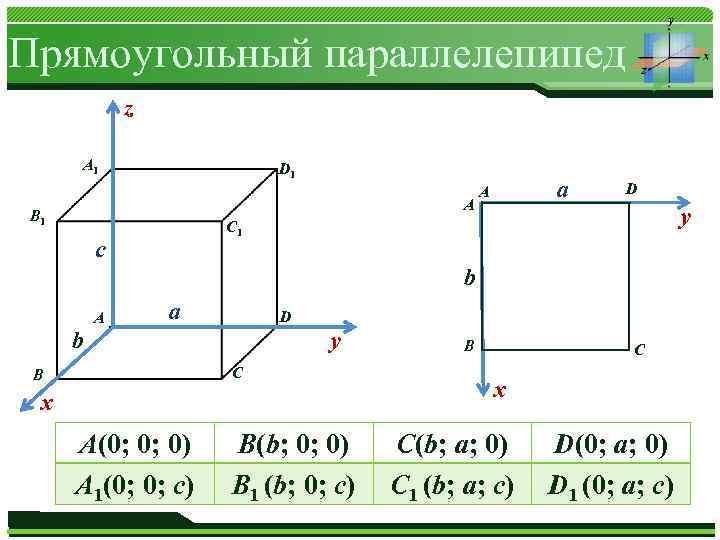Прямоугольный параллелепипед z A 1 D 1 A B 1 а А D y C 1 с b b B A а D y C x А(0; 0; 0) B(b; 0; 0) Журнал «Математика» № 01/2013 А 1(0; 0; с) B 1 (b; 0; с) B C x C(b; a; 0) C 1 (b; a; с) D(0; a; 0) D 1 (0; a; с)

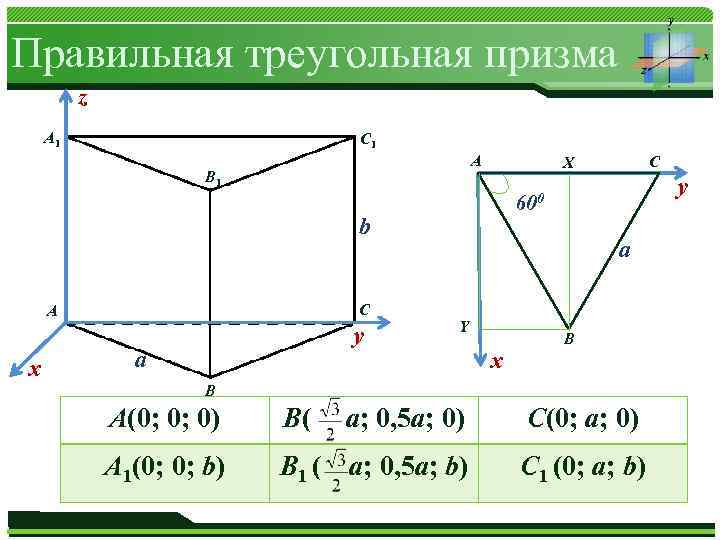Правильная треугольная призма z А 1 C 1 А B 1 C x y а y 600 b А C X а Y x B B А(0; 0; 0) B( a; 0, 5 a; 0) C(0; a; 0) А (0; 0; b) B 1 ( a; 0, 5 a; b) C 1 (0; a; b) 1 Журнал «Математика» № 01/2013

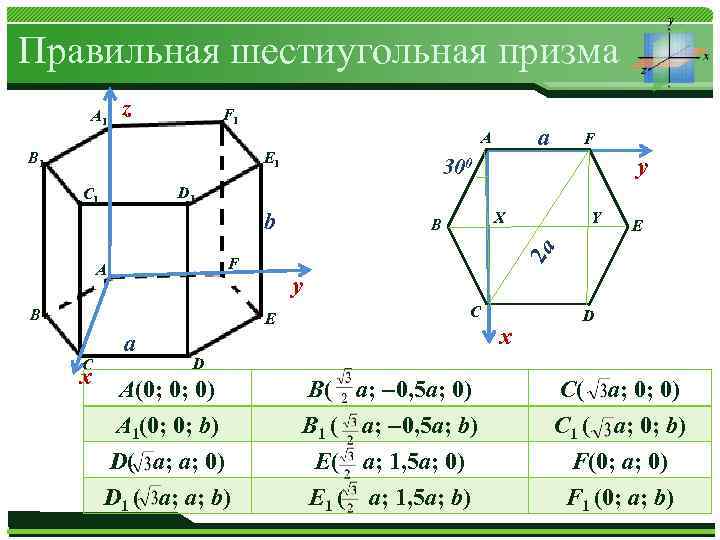Правильная шестиугольная призма А 1 z F 1 а А E 1 B 1 b B E y E а Y X B 2 а F А x y 300 D 1 C F C x D D А(0; 0; 0) А 1(0; 0; b) D( a; a; 0) Журнал «Математика» № 01/2013 D 1 ( a; a; b) B( a; – 0, 5 a; 0) B 1 ( a; – 0, 5 a; b) Е( a; 1, 5 a; 0) Е 1 ( a; 1, 5 a; b) C( а; 0; 0) C 1 ( а; 0; b) F(0; a; 0) F 1 (0; a; b)

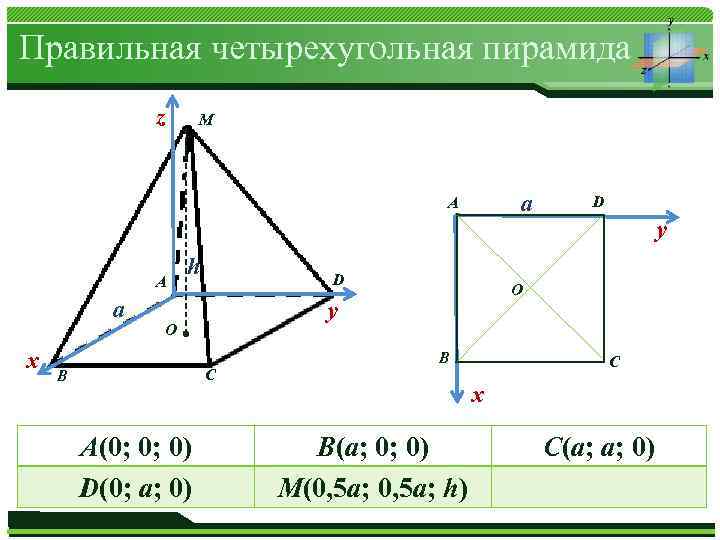Правильная четырехугольная пирамида z M а A A а x B h D C А(0; 0; 0) Журнал «Математика» № 01/2013 D(0; a; 0) y O D B C x B(a; 0; 0) M(0, 5 а; h) C(a; a; 0)

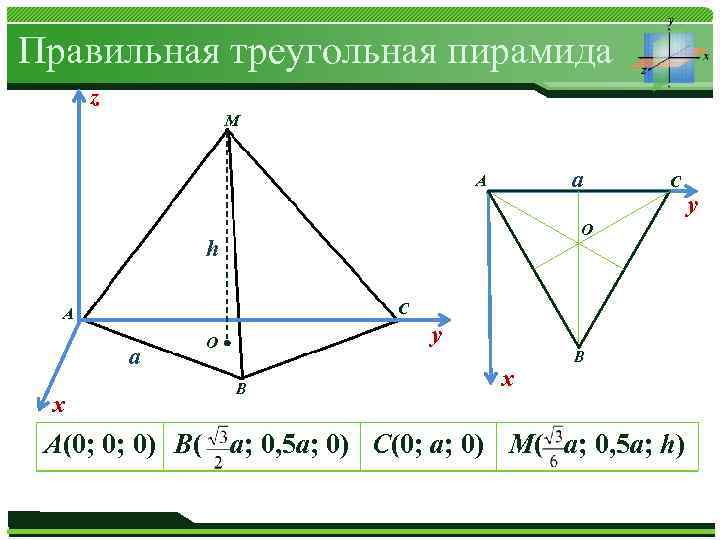Правильная треугольная пирамида z M а А C O h C А а y O B x А(0; 0; 0) B( x B a; 0, 5 a; 0) C(0; a; 0) M( a; 0, 5 a; h) Журнал «Математика» № 01/2013 y

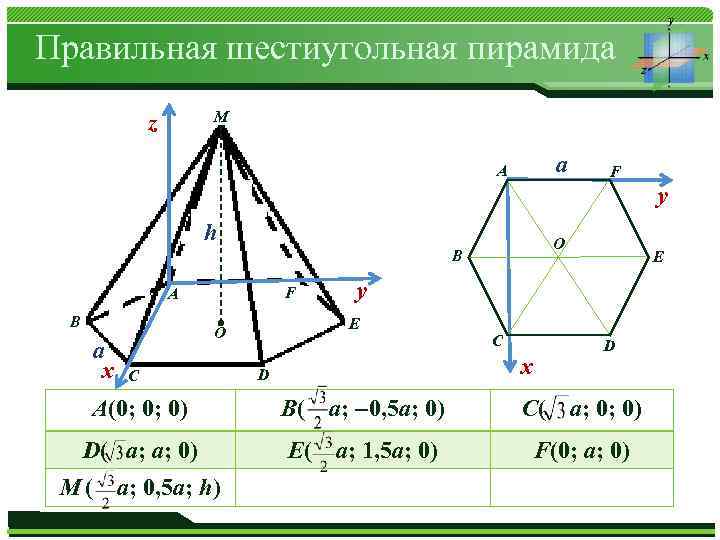Правильная шестиугольная пирамида M z а А F y h O B F А B а x C y E O C D x D А(0; 0; 0) B( a; – 0, 5 a; 0) D( a; a; 0) Е( a; 1, 5 a; 0) Журнал M ( «Математика» № 01/2013 a; 0, 5 a; h) E C( а; 0; 0) F(0; a; 0)

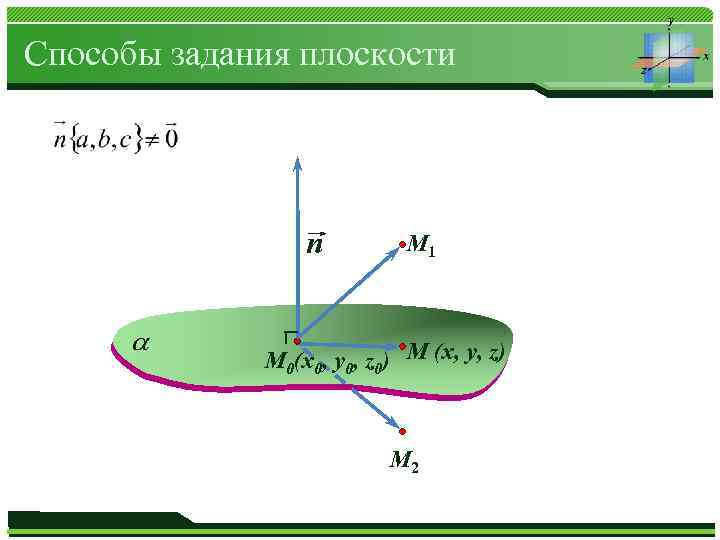Способы задания плоскости n М 1 М 0(x 0, y 0, z 0) М (x, y, z) Журнал «Математика» № 01/2013 М 2

α, проходящей через точку М 0(x 0, y 0, z 0) и перпендикулярной вектору : : где – нормальный вектор плоскости. Журнал «Математика» № 01/2013 n М(x 0, y 0, z 0)

Способы задания прямой l, заданной точкой М 0(x 0, y 0, z 0) и направляющим вектором а : Журнал «Математика» № 01/2013 М 0(x 0, y 0, z 0)

Способы задания прямой М 1(x 1, y 1, z 1) и М 2(x 2, y 2, z 2): а М 1(x 1, y 1, z 1) М 2(x 2, y 2, z 2) Журнал «Математика» № 01/2013

Расстояние между двумя точками Журнал «Математика» № 01/2013