Reservoir Simulation Gridding and Well Modelling Sergey Kurelenkov





































4_-_gridding_and_well_modelling.ppt
- Размер: 4.3 Mегабайта
- Количество слайдов: 81
Описание презентации Reservoir Simulation Gridding and Well Modelling Sergey Kurelenkov по слайдам
 Reservoir Simulation Gridding and Well Modelling Sergey Kurelenkov 2011 (after Ken Sorbie)
Reservoir Simulation Gridding and Well Modelling Sergey Kurelenkov 2011 (after Ken Sorbie)
 Outline • Gridding in Reservoir Simulation • Calculation of Block to Block Flows in Reservoir Simulators • Wells in Reservoir Simulation
Outline • Gridding in Reservoir Simulation • Calculation of Block to Block Flows in Reservoir Simulators • Wells in Reservoir Simulation
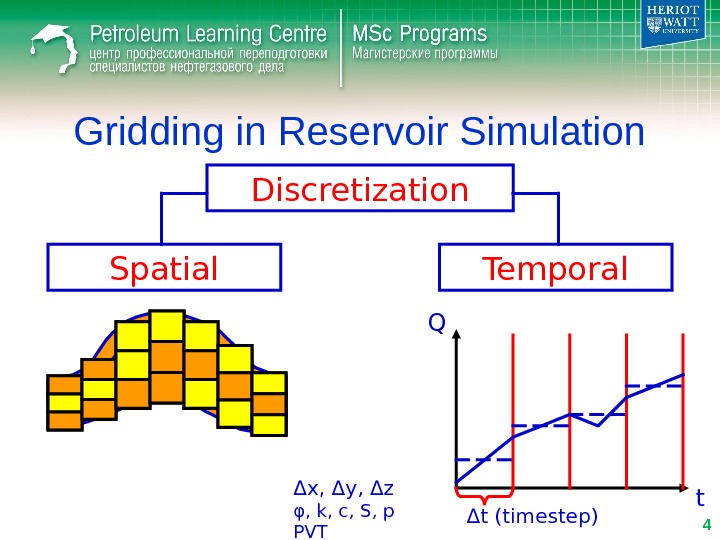
 Gridding in Reservoir Simulation • Reservoir Simulation Model – grid block model of a petroleum reservoir… • Gridding – process of dividing up a reservoir into grid blocks ( spatial discretization ) • Discretization – process of dividing up a continuous quantity into discrete intervals
Gridding in Reservoir Simulation • Reservoir Simulation Model – grid block model of a petroleum reservoir… • Gridding – process of dividing up a reservoir into grid blocks ( spatial discretization ) • Discretization – process of dividing up a continuous quantity into discrete intervals
 Gridding in Reservoir Simulation Discretization Spatial Temporal t. Q Δ t (timestep)Δ x, Δ y, Δ z φ , k, c, S, p PVT
Gridding in Reservoir Simulation Discretization Spatial Temporal t. Q Δ t (timestep)Δ x, Δ y, Δ z φ , k, c, S, p PVT
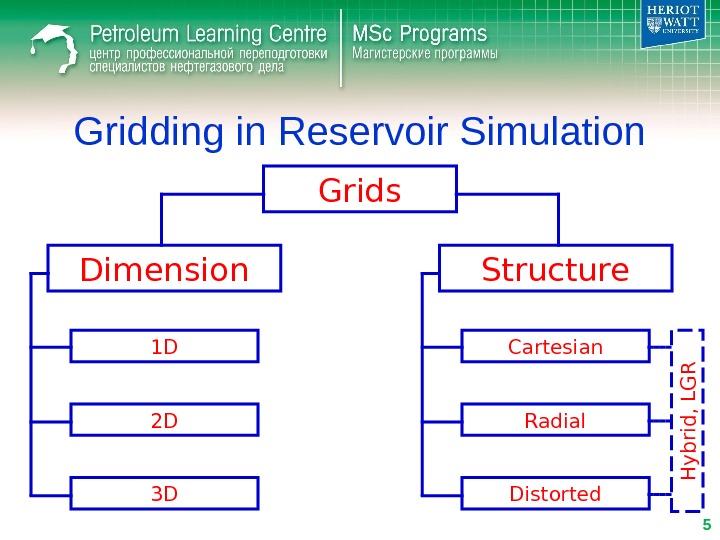
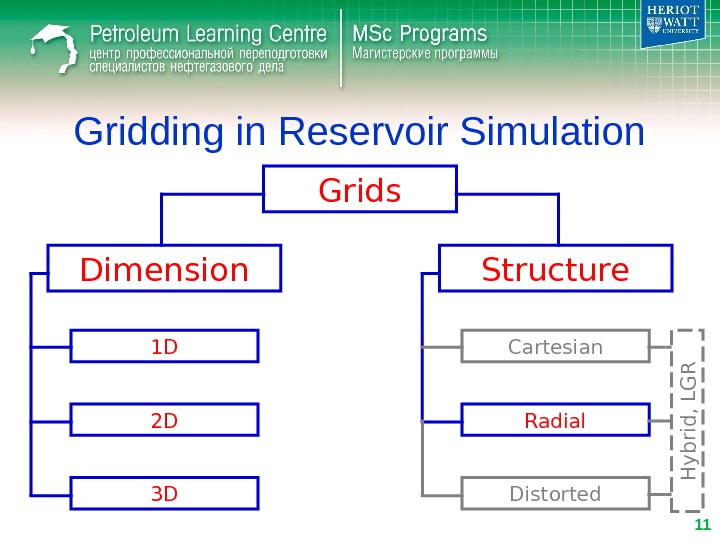
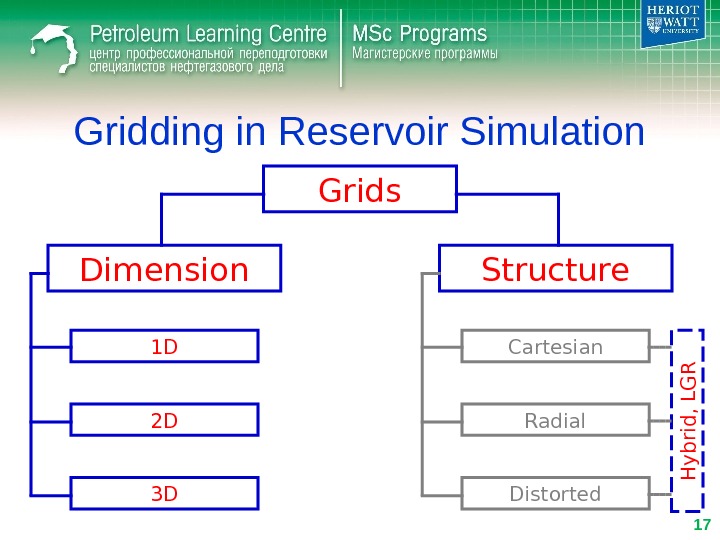
 Gridding in Reservoir Simulation Grids Dimension Structure 1 D 2 D 3 D Cartesian Radial Distorted. H y b rid , L G R
Gridding in Reservoir Simulation Grids Dimension Structure 1 D 2 D 3 D Cartesian Radial Distorted. H y b rid , L G R
 Gridding in Reservoir Simulation Grids Dimension Structure 1 D 2 D 3 D Cartesian Radial Distorted. H y b rid , L G R
Gridding in Reservoir Simulation Grids Dimension Structure 1 D 2 D 3 D Cartesian Radial Distorted. H y b rid , L G R
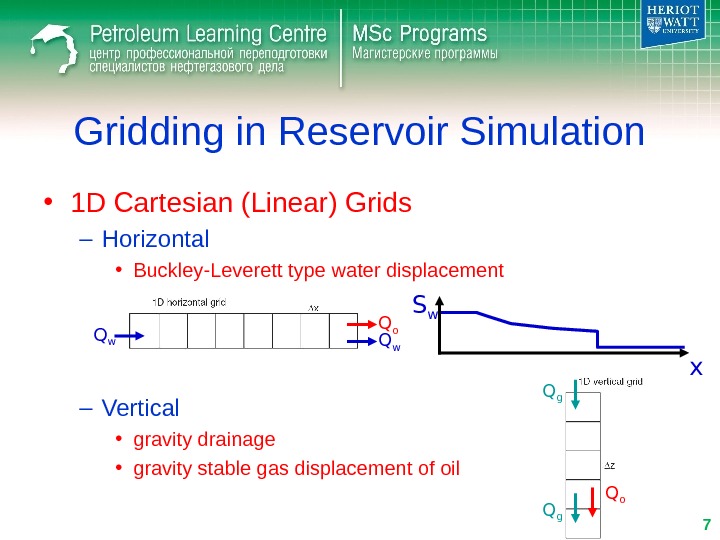
 Gridding in Reservoir Simulation • 1 D Cartesian (Linear) Grids – Horizontal • Buckley-Leverett type water displacement – Vertical • gravity drainage • gravity stable gas displacement of oil x. S w Q w. Q o Q g
Gridding in Reservoir Simulation • 1 D Cartesian (Linear) Grids – Horizontal • Buckley-Leverett type water displacement – Vertical • gravity drainage • gravity stable gas displacement of oil x. S w Q w. Q o Q g
 Gridding in Reservoir Simulation • 2 D Cartesian Grids – Cross-sectional (x/z) • vertical sweep efficiency • water/oil displacements in geostatistically generated cross-section • generation of pseudo-relative permeabilities (2 phase upscaling) • mechanism of gas displacement (importance of gravity)
Gridding in Reservoir Simulation • 2 D Cartesian Grids – Cross-sectional (x/z) • vertical sweep efficiency • water/oil displacements in geostatistically generated cross-section • generation of pseudo-relative permeabilities (2 phase upscaling) • mechanism of gas displacement (importance of gravity)
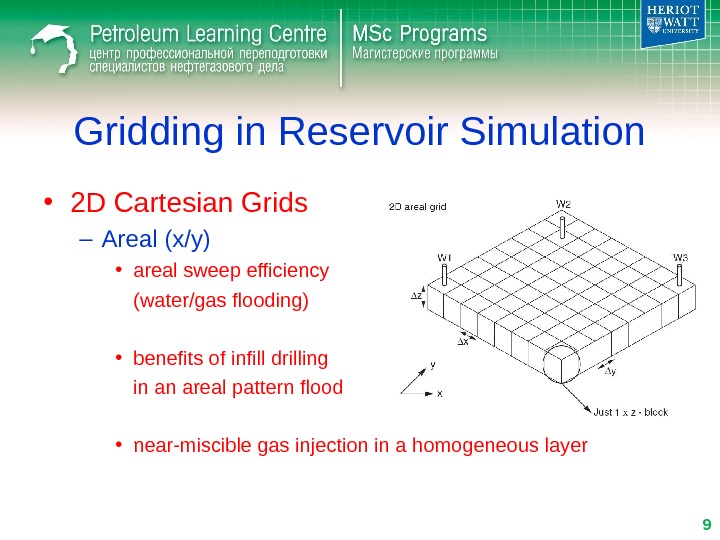
 Gridding in Reservoir Simulation • 2 D Cartesian Grids – Areal (x/y) • areal sweep efficiency (water/gas flooding) • benefits of infill drilling in an areal pattern flood • near-miscible gas injection in a homogeneous layer
Gridding in Reservoir Simulation • 2 D Cartesian Grids – Areal (x/y) • areal sweep efficiency (water/gas flooding) • benefits of infill drilling in an areal pattern flood • near-miscible gas injection in a homogeneous layer
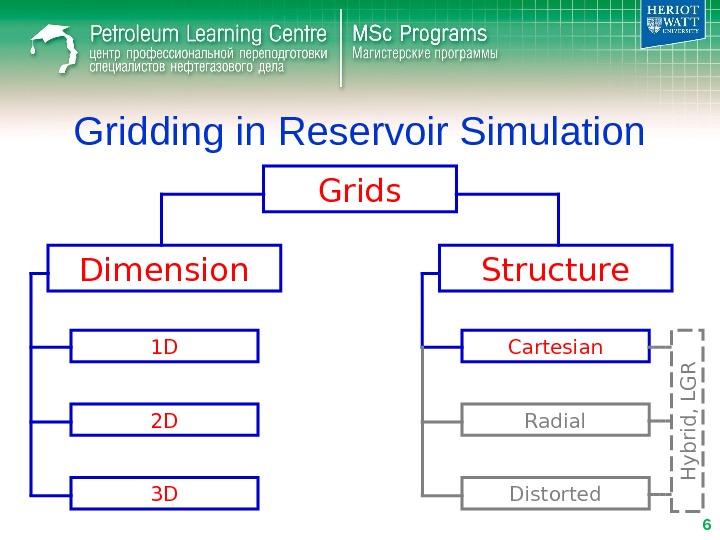
 Gridding in Reservoir Simulation • 3 D Cartesian Grids – Default grid type • easy to set up • less time consuming simulation (equations are derived for this grid) • wide range of field wide reservoir production processes (full field simulation of water/gas flooding and etc. )
Gridding in Reservoir Simulation • 3 D Cartesian Grids – Default grid type • easy to set up • less time consuming simulation (equations are derived for this grid) • wide range of field wide reservoir production processes (full field simulation of water/gas flooding and etc. )
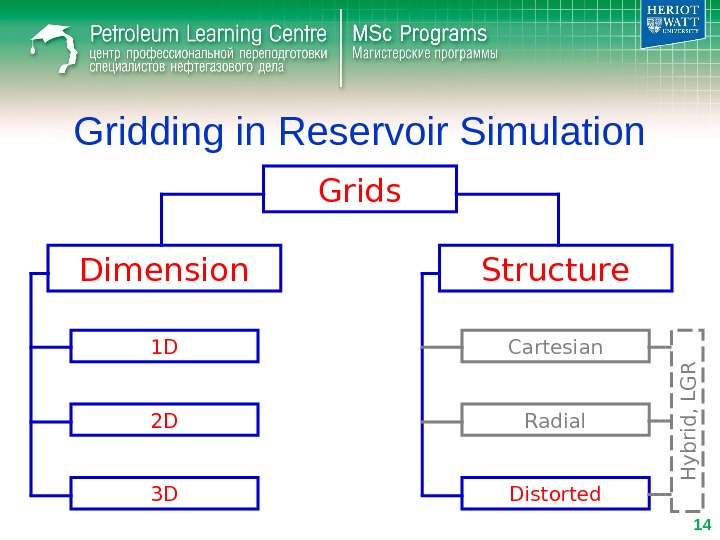
 Gridding in Reservoir Simulation Grids Dimension Structure 1 D 2 D 3 D Cartesian Radial Distorted. H y b rid , L G R
Gridding in Reservoir Simulation Grids Dimension Structure 1 D 2 D 3 D Cartesian Radial Distorted. H y b rid , L G R
 Gridding in Reservoir Simulation • Radial Grids – 1 D • pressure front propagation – 2 D (r/z), 3 D • near wellbore processes (water/gas coning)
Gridding in Reservoir Simulation • Radial Grids – 1 D • pressure front propagation – 2 D (r/z), 3 D • near wellbore processes (water/gas coning)
 Gridding in Reservoir Simulation • Radial Grids – pressure change near well is steep – logarithmically-spaced grid • grid is divided such that wr r r. Pln~)( const)()(1 iir. P 1 iiirrr const 1 i i r r 1 1 ln~)()( i i ii r r r. P
Gridding in Reservoir Simulation • Radial Grids – pressure change near well is steep – logarithmically-spaced grid • grid is divided such that wr r r. Pln~)( const)()(1 iir. P 1 iiirrr const 1 i i r r 1 1 ln~)()( i i ii r r r. P
 Gridding in Reservoir Simulation Grids Dimension Structure 1 D 2 D 3 D Cartesian Radial Distorted. H y b rid , L G R
Gridding in Reservoir Simulation Grids Dimension Structure 1 D 2 D 3 D Cartesian Radial Distorted. H y b rid , L G R
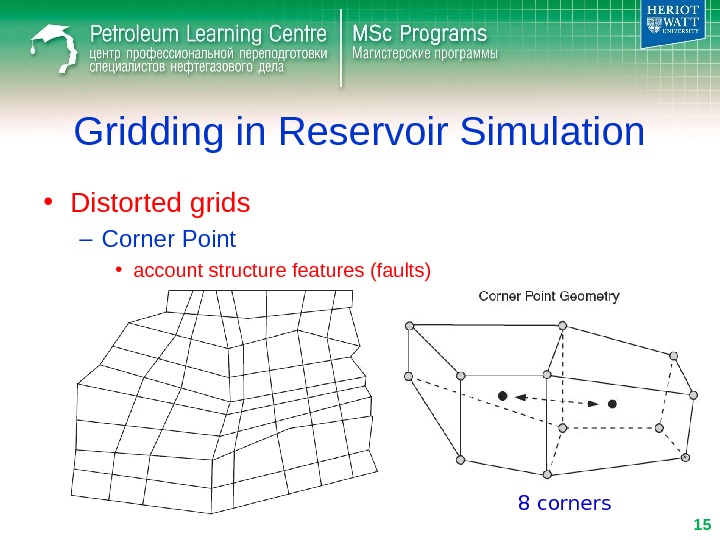
 Gridding in Reservoir Simulation • Distorted grids – Corner Point • account structure features (faults) 8 corners
Gridding in Reservoir Simulation • Distorted grids – Corner Point • account structure features (faults) 8 corners
 Gridding in Reservoir Simulation • Distorted grids – Perpendicular Bisector (PEBI), Voronoi • account structure features (faults) • horizontal well modelling
Gridding in Reservoir Simulation • Distorted grids – Perpendicular Bisector (PEBI), Voronoi • account structure features (faults) • horizontal well modelling
 Gridding in Reservoir Simulation Grids Dimension Structure 1 D 2 D 3 D Cartesian Radial Distorted. H y b rid , L G R
Gridding in Reservoir Simulation Grids Dimension Structure 1 D 2 D 3 D Cartesian Radial Distorted. H y b rid , L G R
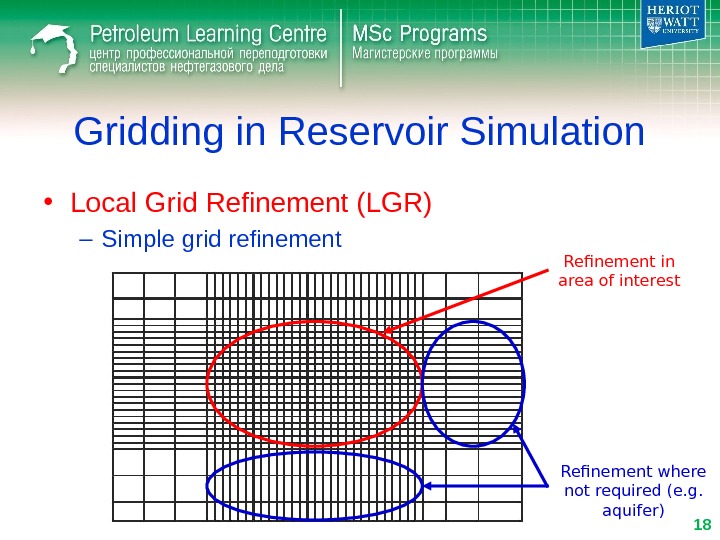
 Gridding in Reservoir Simulation • Local Grid Refinement (LGR) – Simple grid refinement Refinement in area of interest Refinement where not required (e. g. aquifer)
Gridding in Reservoir Simulation • Local Grid Refinement (LGR) – Simple grid refinement Refinement in area of interest Refinement where not required (e. g. aquifer)
 Gridding in Reservoir Simulation • Local Grid Refinement (LGR) – Local Grid Refinement in area of interest Keep coarse grid where not required (e. g. aquifer)
Gridding in Reservoir Simulation • Local Grid Refinement (LGR) – Local Grid Refinement in area of interest Keep coarse grid where not required (e. g. aquifer)
 Gridding in Reservoir Simulation • Local Grid Refinement (LGR) – Hybrid Grid Local Grid Refinement
Gridding in Reservoir Simulation • Local Grid Refinement (LGR) – Hybrid Grid Local Grid Refinement
 Gridding in Reservoir Simulation • Local Grid Refinement (LGR) – Hybrid Grid Local Grid Refinement
Gridding in Reservoir Simulation • Local Grid Refinement (LGR) – Hybrid Grid Local Grid Refinement
 Gridding in Reservoir Simulation • Distorted grids – Faults modelling • Non-neighbor connections (NNC)
Gridding in Reservoir Simulation • Distorted grids – Faults modelling • Non-neighbor connections (NNC)
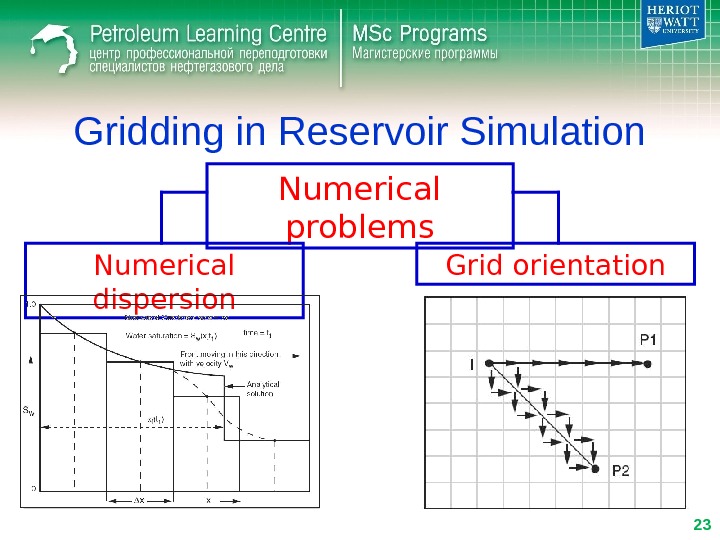
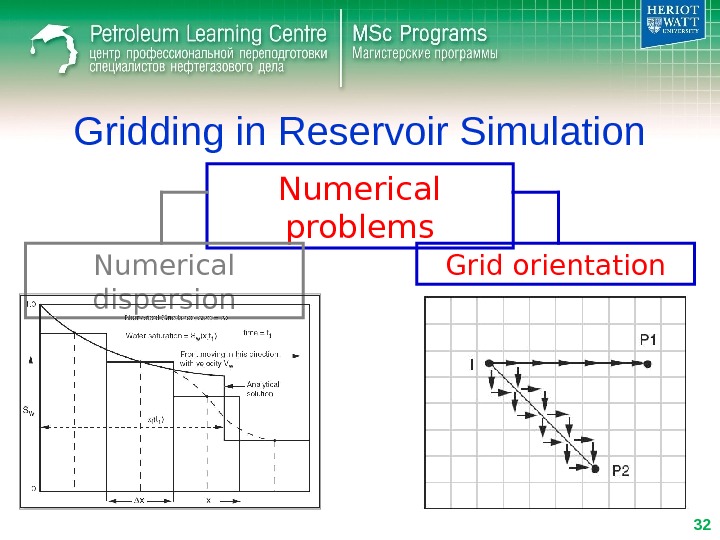
 Gridding in Reservoir Simulation Numerical problems Numerical dispersion Grid orientation
Gridding in Reservoir Simulation Numerical problems Numerical dispersion Grid orientation
 Gridding in Reservoir Simulation Numerical problems Numerical dispersion Grid orientation
Gridding in Reservoir Simulation Numerical problems Numerical dispersion Grid orientation
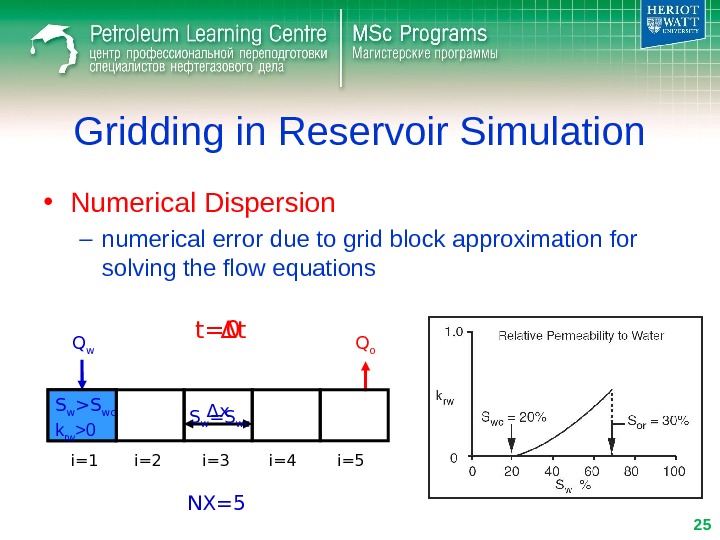
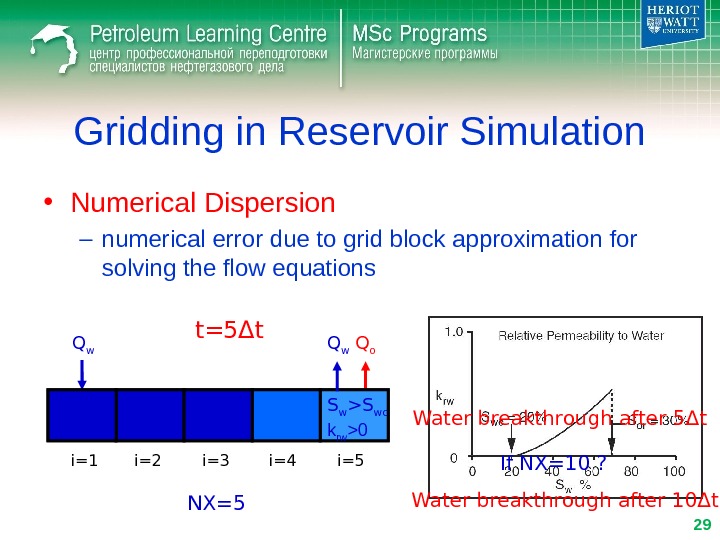
 Gridding in Reservoir Simulation • Numerical Dispersion – numerical error due to grid block approximation for solving the flow equations Q w Q o i=1 i=2 i=3 i=4 i=5Δ x S w =S wct= Δ t 0 NX=5 S w >S wc k rw >
Gridding in Reservoir Simulation • Numerical Dispersion – numerical error due to grid block approximation for solving the flow equations Q w Q o i=1 i=2 i=3 i=4 i=5Δ x S w =S wct= Δ t 0 NX=5 S w >S wc k rw >
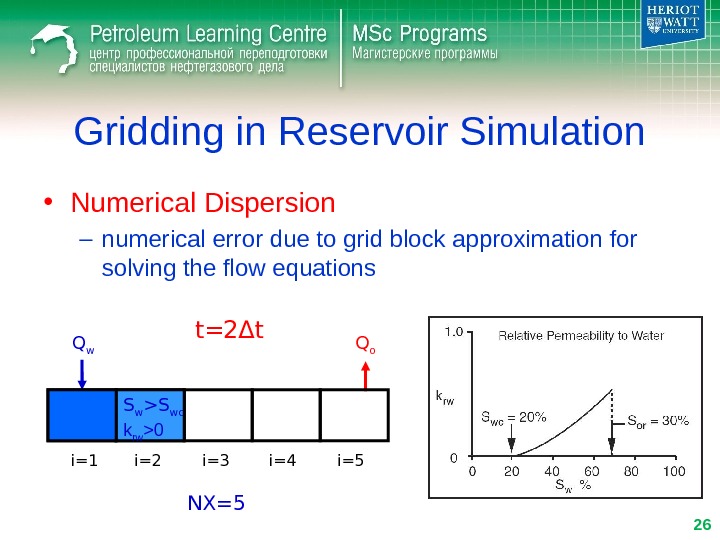
 Gridding in Reservoir Simulation • Numerical Dispersion – numerical error due to grid block approximation for solving the flow equations Q w Q o i=1 i=2 i=3 i=4 i=5 t= 2 Δ t NX=5 S w >S wc k rw >
Gridding in Reservoir Simulation • Numerical Dispersion – numerical error due to grid block approximation for solving the flow equations Q w Q o i=1 i=2 i=3 i=4 i=5 t= 2 Δ t NX=5 S w >S wc k rw >
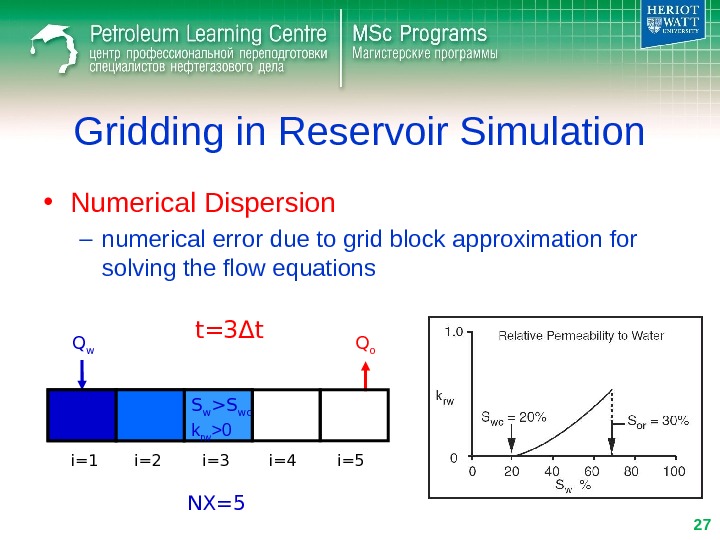
 Gridding in Reservoir Simulation • Numerical Dispersion – numerical error due to grid block approximation for solving the flow equations Q w Q o i=1 i=2 i=3 i=4 i=5 t= 3 Δ t NX=5 S w >S wc k rw >
Gridding in Reservoir Simulation • Numerical Dispersion – numerical error due to grid block approximation for solving the flow equations Q w Q o i=1 i=2 i=3 i=4 i=5 t= 3 Δ t NX=5 S w >S wc k rw >
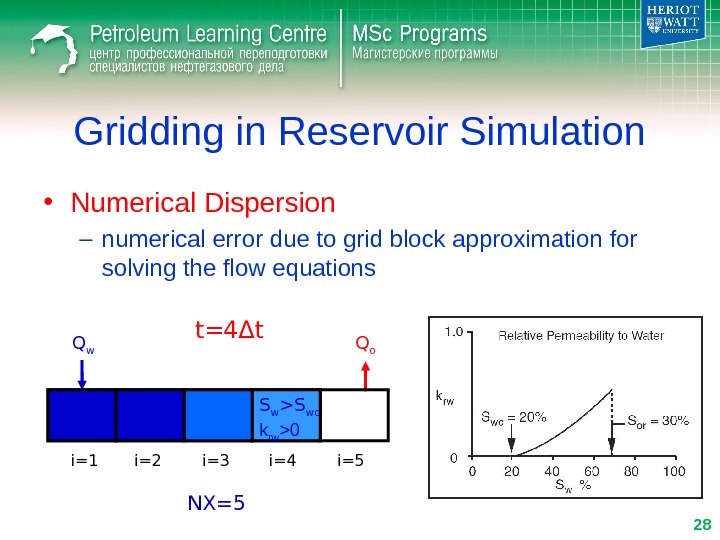
 Gridding in Reservoir Simulation • Numerical Dispersion – numerical error due to grid block approximation for solving the flow equations Q w Q o i=1 i=2 i=3 i=4 i=5 t= 4 Δ t NX=5 S w >S wc k rw >
Gridding in Reservoir Simulation • Numerical Dispersion – numerical error due to grid block approximation for solving the flow equations Q w Q o i=1 i=2 i=3 i=4 i=5 t= 4 Δ t NX=5 S w >S wc k rw >
 Gridding in Reservoir Simulation • Numerical Dispersion – numerical error due to grid block approximation for solving the flow equations Q w Q o i=1 i=2 i=3 i=4 i=5 t= 5 Δ t NX=5 S w >S wc k rw >0 Q w Water breakthrough after 5 Δ t If NX=10 ? Water breakthrough after 10 Δ t’
Gridding in Reservoir Simulation • Numerical Dispersion – numerical error due to grid block approximation for solving the flow equations Q w Q o i=1 i=2 i=3 i=4 i=5 t= 5 Δ t NX=5 S w >S wc k rw >0 Q w Water breakthrough after 5 Δ t If NX=10 ? Water breakthrough after 10 Δ t’
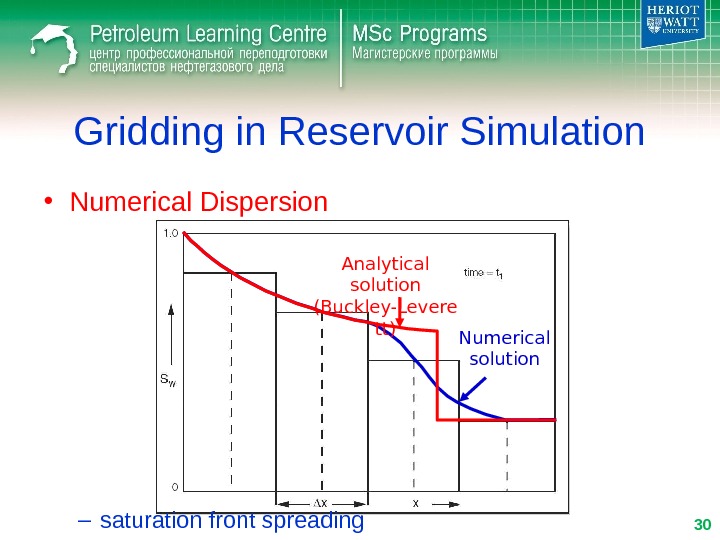
 Gridding in Reservoir Simulation • Numerical Dispersion – saturation front spreading Analytical solution (Buckley-Levere tt) Numerical solution
Gridding in Reservoir Simulation • Numerical Dispersion – saturation front spreading Analytical solution (Buckley-Levere tt) Numerical solution
 Gridding in Reservoir Simulation • Numerical Dispersion – Methods of reducing • Grid refinement (increase in number of grid blocks) • Use of Pseudo-relative permeabilities (2 phase upscaling) • Use of alternative simulation scheme (Streamline simulation) S wcr
Gridding in Reservoir Simulation • Numerical Dispersion – Methods of reducing • Grid refinement (increase in number of grid blocks) • Use of Pseudo-relative permeabilities (2 phase upscaling) • Use of alternative simulation scheme (Streamline simulation) S wcr
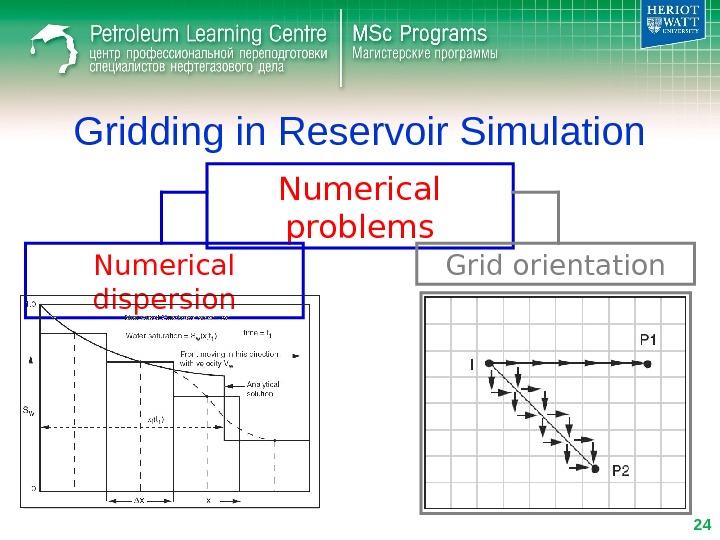
 Gridding in Reservoir Simulation Numerical problems Numerical dispersion Grid orientation
Gridding in Reservoir Simulation Numerical problems Numerical dispersion Grid orientation
 Gridding in Reservoir Simulation • Grid Orientation effect – arises when the fluid flow both oriented with the principal and diagonal grid direction L L P 1 P
Gridding in Reservoir Simulation • Grid Orientation effect – arises when the fluid flow both oriented with the principal and diagonal grid direction L L P 1 P
 Gridding in Reservoir Simulation • Grid Orientation effect – Methods of reducing • Grid refinement (increase in number of grid blocks) • Use of distorted grids (PEBI) • Use of improved numerical schemes (9 -point) • Use of alternative simulation scheme (Streamline simulation) 5 -point 9 -point
Gridding in Reservoir Simulation • Grid Orientation effect – Methods of reducing • Grid refinement (increase in number of grid blocks) • Use of distorted grids (PEBI) • Use of improved numerical schemes (9 -point) • Use of alternative simulation scheme (Streamline simulation) 5 -point 9 -point
 Gridding in Reservoir Simulation • Streamline Simulation Pressure Streamlines Saturation
Gridding in Reservoir Simulation • Streamline Simulation Pressure Streamlines Saturation
 Gridding in Reservoir Simulation • Issues in Choosing Reservoir Simulation Grid – Grid Dimension • 1 D, 2 D, 3 D ? – Grid Geometry/Structure • Cartesian, Distorted, LGR ? – Grid Fineness/Coarseness • Grid block size (number of grid blocks) ? should be related to the simplicity/complexity of the problem
Gridding in Reservoir Simulation • Issues in Choosing Reservoir Simulation Grid – Grid Dimension • 1 D, 2 D, 3 D ? – Grid Geometry/Structure • Cartesian, Distorted, LGR ? – Grid Fineness/Coarseness • Grid block size (number of grid blocks) ? should be related to the simplicity/complexity of the problem
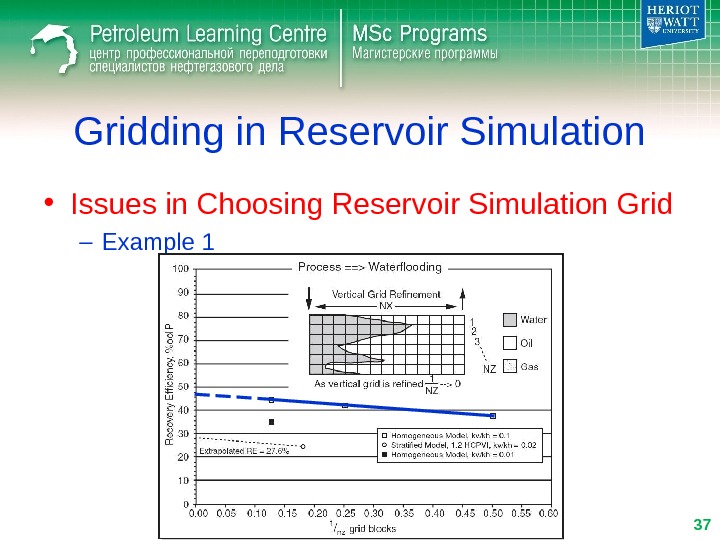
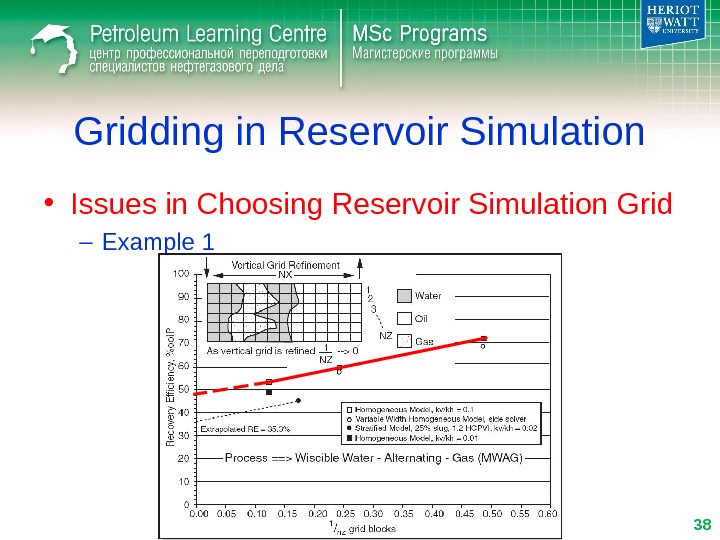
 Gridding in Reservoir Simulation • Issues in Choosing Reservoir Simulation Grid – Example
Gridding in Reservoir Simulation • Issues in Choosing Reservoir Simulation Grid – Example
 • Issues in Choosing Reservoir Simulation Grid – Example 1 Gridding in Reservoir Simulation
• Issues in Choosing Reservoir Simulation Grid – Example 1 Gridding in Reservoir Simulation
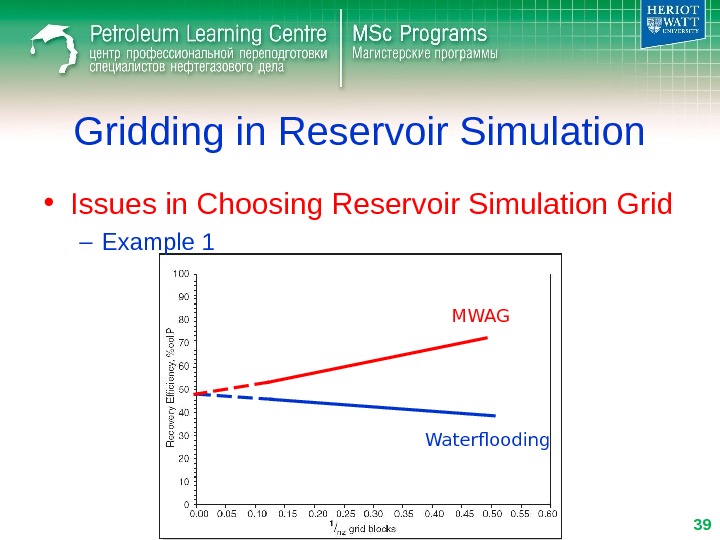
 Gridding in Reservoir Simulation • Issues in Choosing Reservoir Simulation Grid – Example 1 MWAG Waterflooding
Gridding in Reservoir Simulation • Issues in Choosing Reservoir Simulation Grid – Example 1 MWAG Waterflooding
 • Issues in Choosing Reservoir Simulation Grid – Example 2 Gridding in Reservoir Simulation
• Issues in Choosing Reservoir Simulation Grid – Example 2 Gridding in Reservoir Simulation
 Outline • Gridding in Reservoir Simulation • Calculation of Block to Block Flows in Reservoir Simulators • Wells in Reservoir Simulation
Outline • Gridding in Reservoir Simulation • Calculation of Block to Block Flows in Reservoir Simulators • Wells in Reservoir Simulation
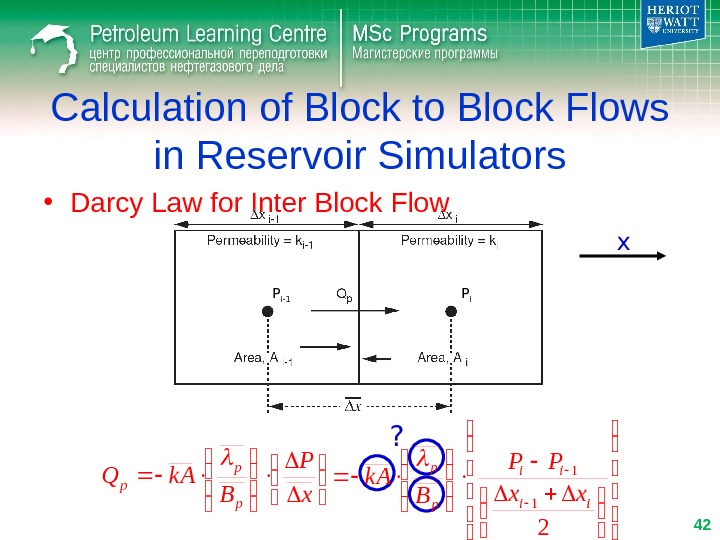
 Calculation of Block to Block Flows in Reservoir Simulators • Darcy Law for Inter Block Flow x P B k AQ p p p x P i-1 ? 2 1 1 ii ii p p xx PP B k
Calculation of Block to Block Flows in Reservoir Simulators • Darcy Law for Inter Block Flow x P B k AQ p p p x P i-1 ? 2 1 1 ii ii p p xx PP B k
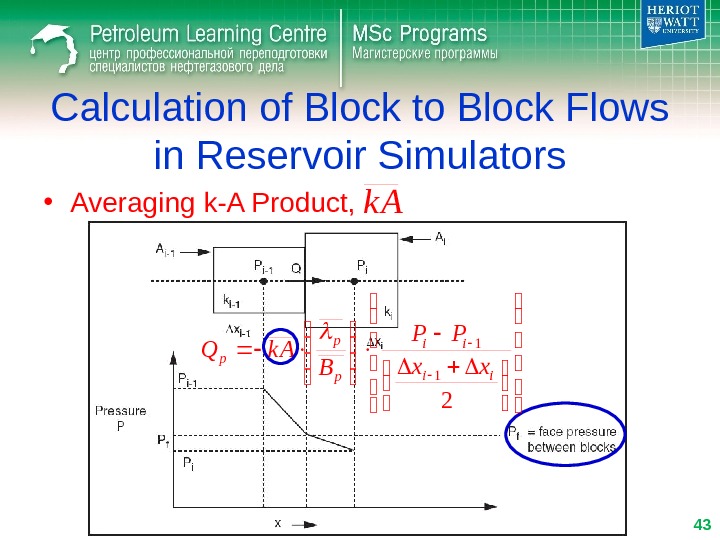
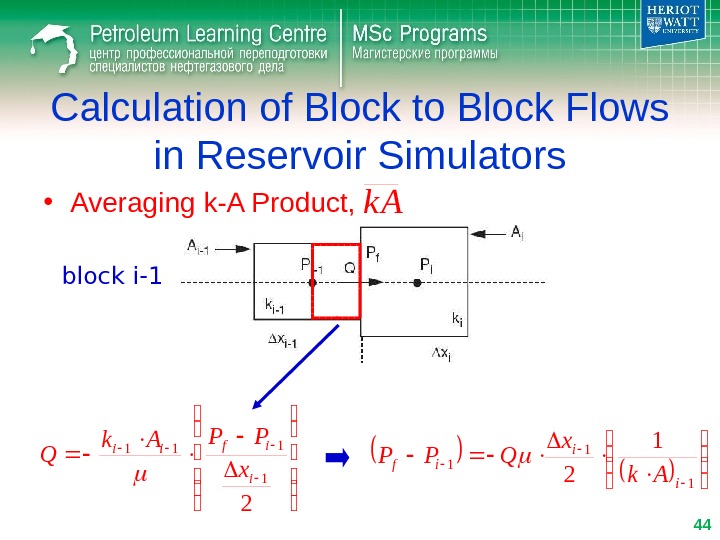
 Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, k A 2 1 1 ii ii p p p xx PP B k AQ
Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, k A 2 1 1 ii ii p p p xx PP B k AQ
 Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, 2 1 111 i ifii x PPAk Q 1 1 2 i i if Ak x QPP block i-1 44 k
Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, 2 1 111 i ifii x PPAk Q 1 1 2 i i if Ak x QPP block i-1 44 k
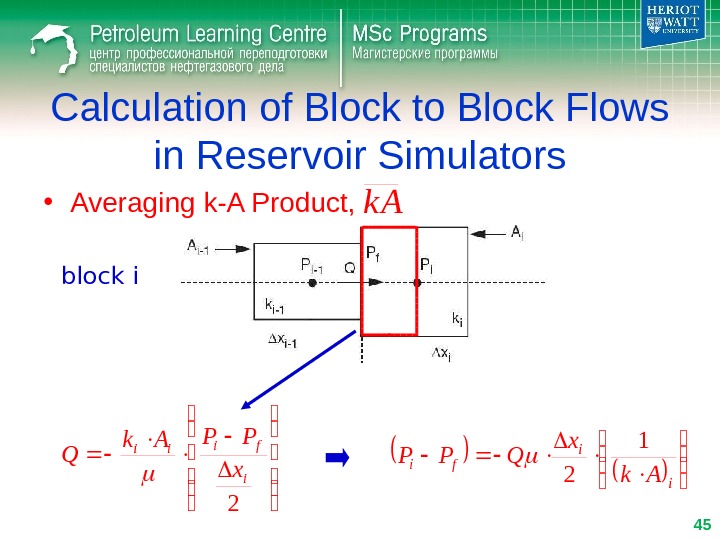
 Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, 2 i fiii x PPAk Q i i fi Ak x QPP 1 2 block i 45 k
Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, 2 i fiii x PPAk Q i i fi Ak x QPP 1 2 block i 45 k
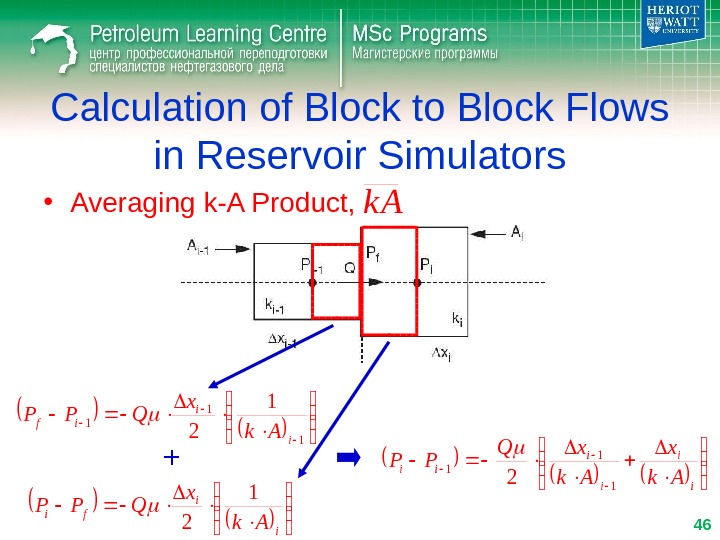
 i i ii Ak x. Q PP 1 1 1 2 Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, 1 1 2 i i if Ak x QPP i i fi Ak x QPP 1 2 + 46 k
i i ii Ak x. Q PP 1 1 1 2 Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, 1 1 2 i i if Ak x QPP i i fi Ak x QPP 1 2 + 46 k
 i i ii Ak x. Q PP 1 1 1 2 Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, 1 1 1 21 ii i i PP Ak x Q 47 k
i i ii Ak x. Q PP 1 1 1 2 Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, 1 1 1 21 ii i i PP Ak x Q 47 k
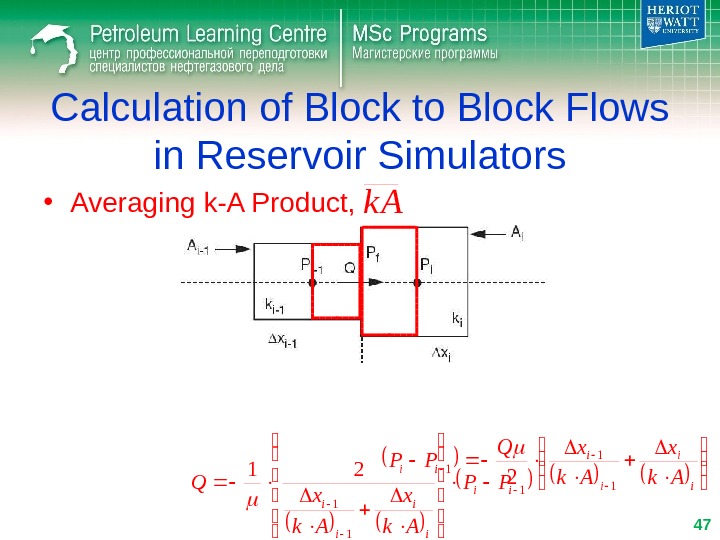
 2 1 1 ii ii xx PPk A Q Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, 1 1 1 21 ii i i PP Ak x Q i iii Ak xxx k A 1 11 2 2 48 k
2 1 1 ii ii xx PPk A Q Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, 1 1 1 21 ii i i PP Ak x Q i iii Ak xxx k A 1 11 2 2 48 k
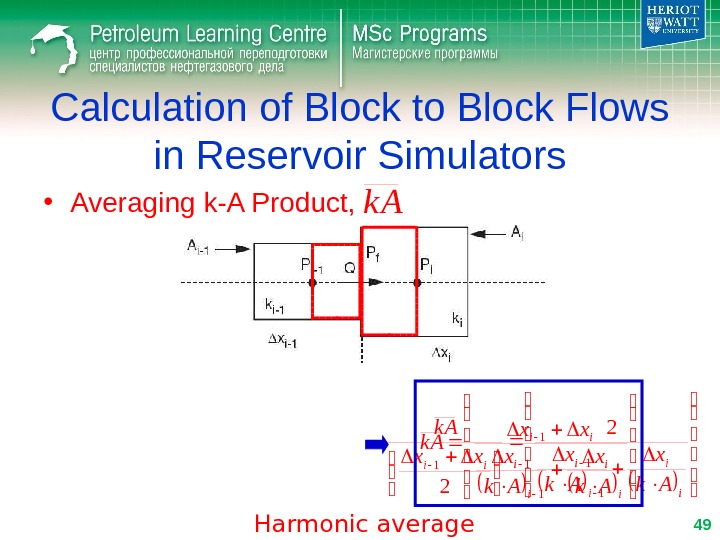
 Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, i iii Ak xxx k A 1 11 2 2 i i ii Ak x xx k A 1 1 1 Harmonic average 49 k
Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, i iii Ak xxx k A 1 11 2 2 i i ii Ak x xx k A 1 1 1 Harmonic average 49 k
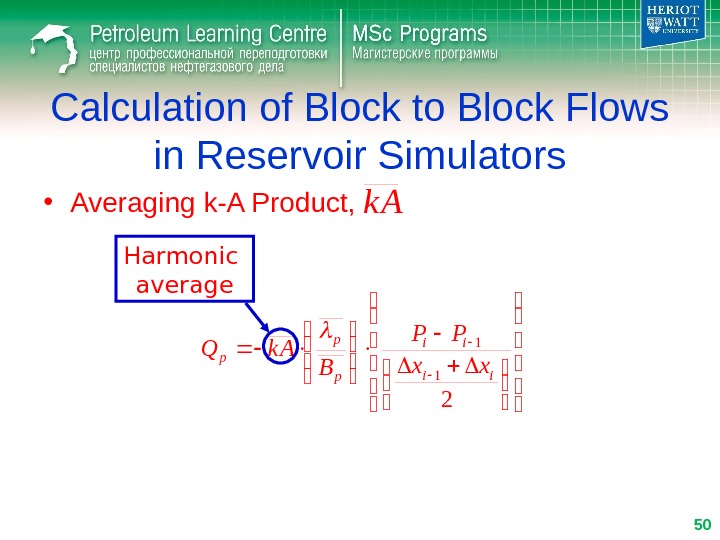
 Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, 2 1 1 ii ii p p p xx PP B k AQ Harmonic average 50 k
Calculation of Block to Block Flows in Reservoir Simulators • Averaging k-A Product, 2 1 1 ii ii p p p xx PP B k AQ Harmonic average 50 k
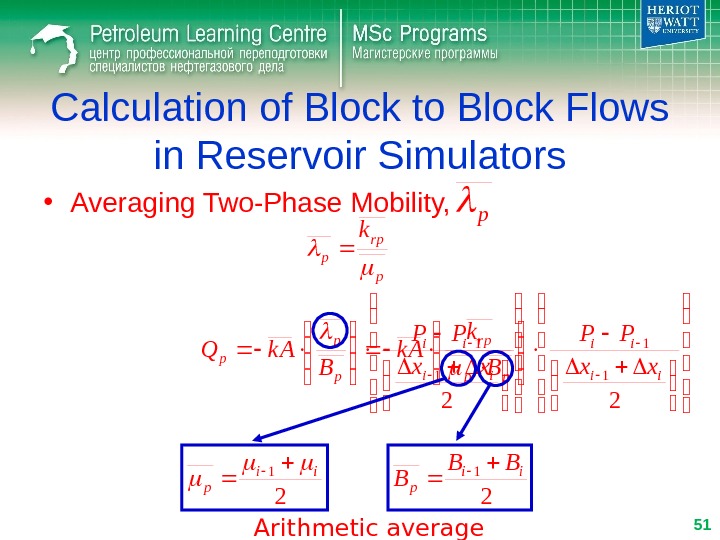
 Calculation of Block to Block Flows in Reservoir Simulators • Averaging Two-Phase Mobility, p 2 1 1 ii ii p p p xx PP B k AQ p rp p k 2 1 1 ii ii pp rp xx PP B k k A 2 1 ii p BB B Arithmetic average
Calculation of Block to Block Flows in Reservoir Simulators • Averaging Two-Phase Mobility, p 2 1 1 ii ii p p p xx PP B k AQ p rp p k 2 1 1 ii ii pp rp xx PP B k k A 2 1 ii p BB B Arithmetic average
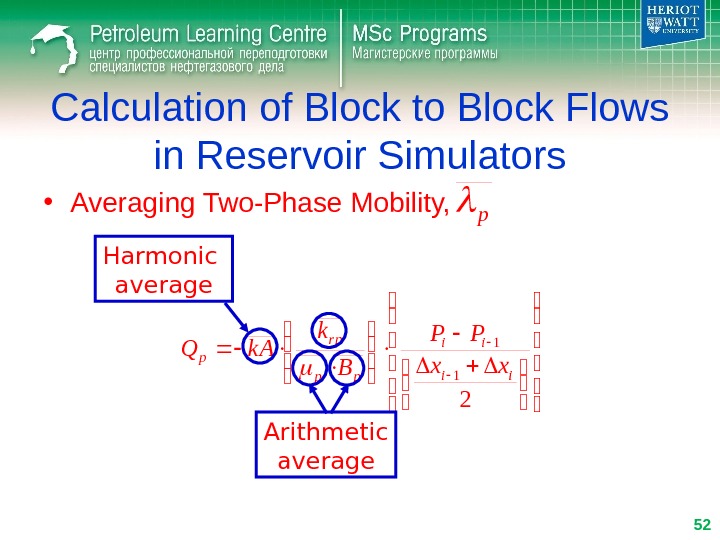
 Calculation of Block to Block Flows in Reservoir Simulators • Averaging Two-Phase Mobility, 2 1 1 ii ii pp rp p xx PP B k k AQ Harmonic average Arithmetic average 52 p
Calculation of Block to Block Flows in Reservoir Simulators • Averaging Two-Phase Mobility, 2 1 1 ii ii pp rp p xx PP B k k AQ Harmonic average Arithmetic average 52 p
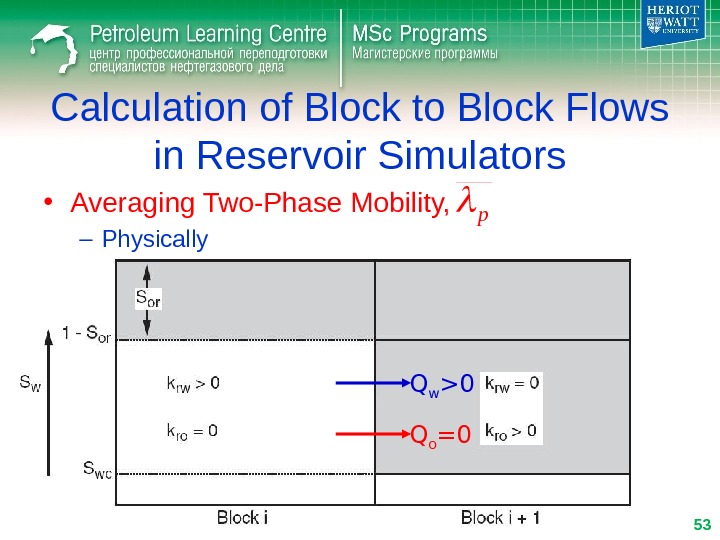
 Calculation of Block to Block Flows in Reservoir Simulators • Averaging Two-Phase Mobility, – Physically Q w >0 Q o =0 53 p
Calculation of Block to Block Flows in Reservoir Simulators • Averaging Two-Phase Mobility, – Physically Q w >0 Q o =0 53 p
 • Averaging Two-Phase Mobility, – Harmonic average (kh ) ? Calculation of Block to Block Flows in Reservoir Simulators k hrw =0 k hro =0 54 p
• Averaging Two-Phase Mobility, – Harmonic average (kh ) ? Calculation of Block to Block Flows in Reservoir Simulators k hrw =0 k hro =0 54 p
 • Averaging Two-Phase Mobility, – Arithmetic average (ka ) ? Calculation of Block to Block Flows in Reservoir Simulators k arw >0 k aro >0 55 p
• Averaging Two-Phase Mobility, – Arithmetic average (ka ) ? Calculation of Block to Block Flows in Reservoir Simulators k arw >0 k aro >0 55 p
 • Averaging Two-Phase Mobility, – Upstream value ? Calculation of Block to Block Flows in Reservoir Simulators k urw >0 k uro =0 56 p
• Averaging Two-Phase Mobility, – Upstream value ? Calculation of Block to Block Flows in Reservoir Simulators k urw >0 k uro =0 56 p
 • Averaging Two-Phase Mobility, – Upstream value ? Calculation of Block to Block Flows in Reservoir Simulators k urw =0 k uro >0 57 p
• Averaging Two-Phase Mobility, – Upstream value ? Calculation of Block to Block Flows in Reservoir Simulators k urw =0 k uro >0 57 p
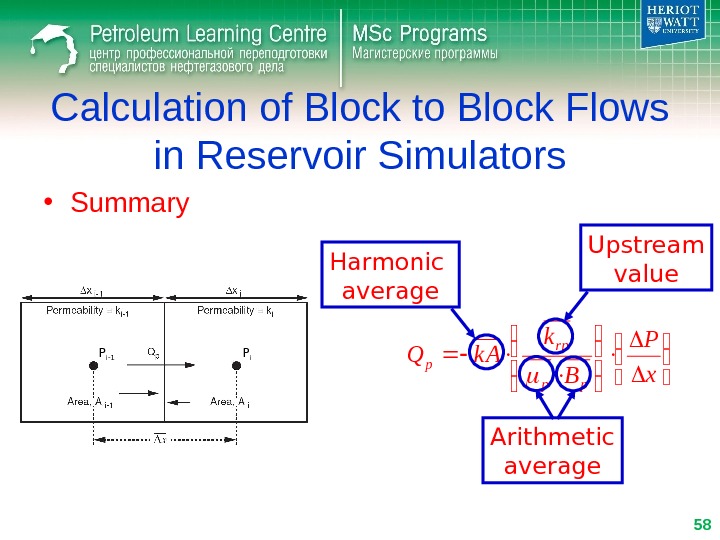
 Calculation of Block to Block Flows in Reservoir Simulators • Summary x P B k k AQ pp rp p Harmonic average Arithmetic average Upstream value P i-
Calculation of Block to Block Flows in Reservoir Simulators • Summary x P B k k AQ pp rp p Harmonic average Arithmetic average Upstream value P i-
 Outline • Gridding in Reservoir Simulation • Calculation of Block to Block Flows in Reservoir Simulators • Wells in Reservoir Simulation
Outline • Gridding in Reservoir Simulation • Calculation of Block to Block Flows in Reservoir Simulators • Wells in Reservoir Simulation
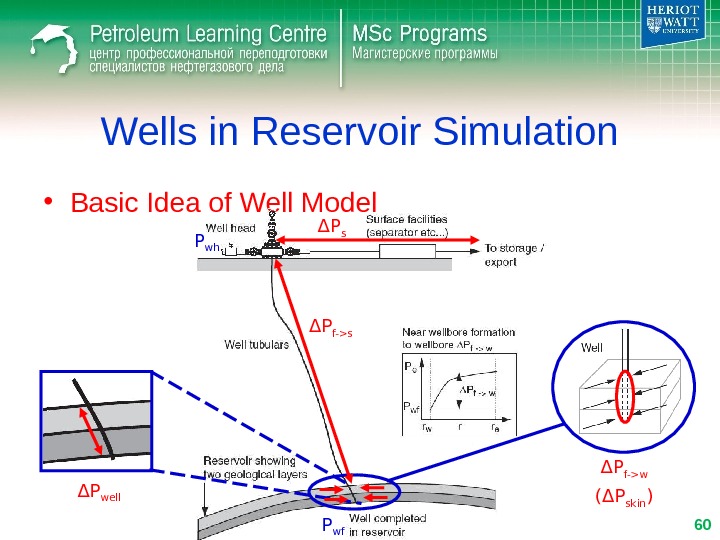
 • Basic Idea of Well Model Wells in Reservoir Simulation Δ P f->w ( Δ P skin )Δ P well Δ P f->sΔ P s P wh P wf
• Basic Idea of Well Model Wells in Reservoir Simulation Δ P f->w ( Δ P skin )Δ P well Δ P f->sΔ P s P wh P wf
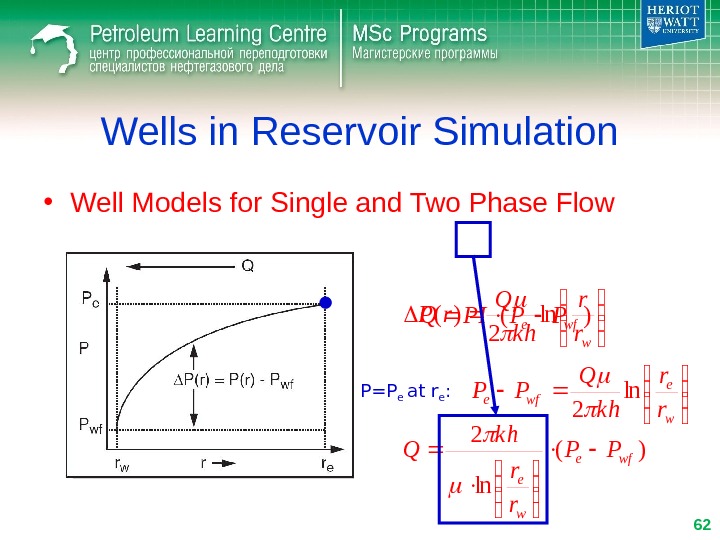
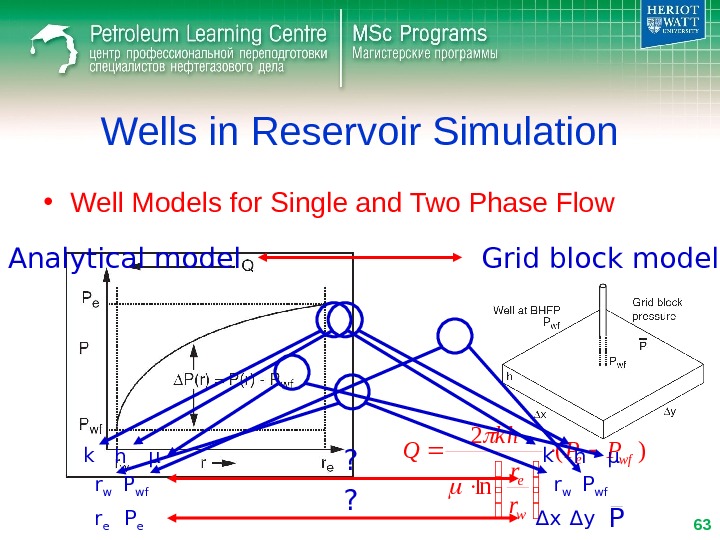
 Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow)(wfe. PPPIQ Givens Controls P wf Q P wf. Q or Limits
Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow)(wfe. PPPIQ Givens Controls P wf Q P wf. Q or Limits
 Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow)(wfe. PPPIQ wr r k h Q r. Pln 2 )( ln 2 wfe w e PP r r k h Q P=P e at r e : w e wfe r r k h Q PPln
Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow)(wfe. PPPIQ wr r k h Q r. Pln 2 )( ln 2 wfe w e PP r r k h Q P=P e at r e : w e wfe r r k h Q PPln
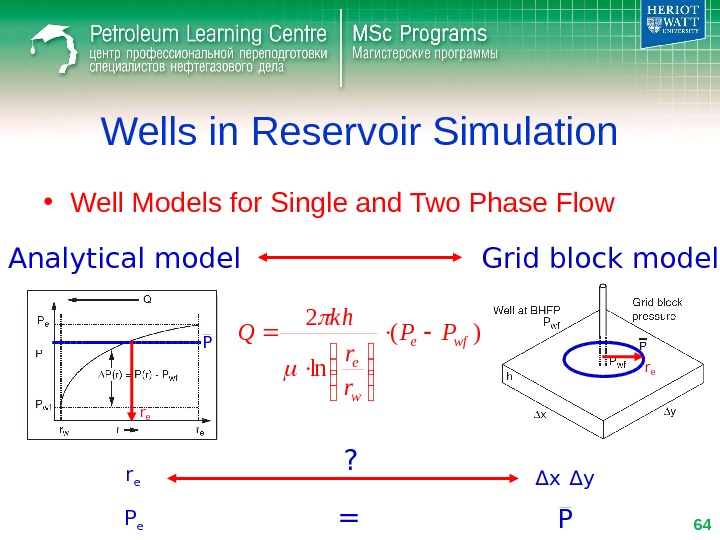
 Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow)( ln 2 wfe w e PP r r k h Q Analytical model Grid block model k h μ r er w P wf P e k h μ r w P wf Δ x Δ y P? ?
Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow)( ln 2 wfe w e PP r r k h Q Analytical model Grid block model k h μ r er w P wf P e k h μ r w P wf Δ x Δ y P? ?
 Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow)( ln 2 wfe w e PP r r k h Q Analytical model Grid block model r e P e Δ x Δ y P = ? P r e
Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow)( ln 2 wfe w e PP r r k h Q Analytical model Grid block model r e P e Δ x Δ y P = ? P r e
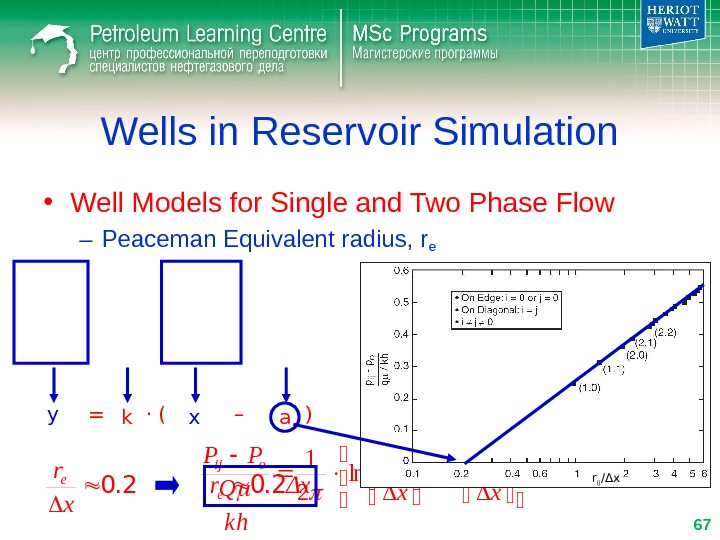
 Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Peaceman Equivalent radius, re 2 D Areal grid r er w r ij i, j P 0 P ij Δ xΔ x w wf r r k h Q Pr. Pln 2 )( e ij oij r r k h Q PPln 2 e ijoij r r k h Q PP ln
Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Peaceman Equivalent radius, re 2 D Areal grid r er w r ij i, j P 0 P ij Δ xΔ x w wf r r k h Q Pr. Pln 2 )( e ij oij r r k h Q PPln 2 e ijoij r r k h Q PP ln
 Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Peaceman Equivalent radius, re e ijoij r r k h Q PP ln 2 1 x r r x x r r reij e ij lnln x r k h Q PPeijoi j lnln
Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Peaceman Equivalent radius, re e ijoij r r k h Q PP ln 2 1 x r r x x r r reij e ij lnln x r k h Q PPeijoi j lnln
 Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Peaceman Equivalent radius, re x r k h Q PPeijoi j lnln 2 1 y = k · ( x – a ) r ij / Δ x 0. 2 x reΔxre 0.
Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Peaceman Equivalent radius, re x r k h Q PPeijoi j lnln 2 1 y = k · ( x – a ) r ij / Δ x 0. 2 x reΔxre 0.
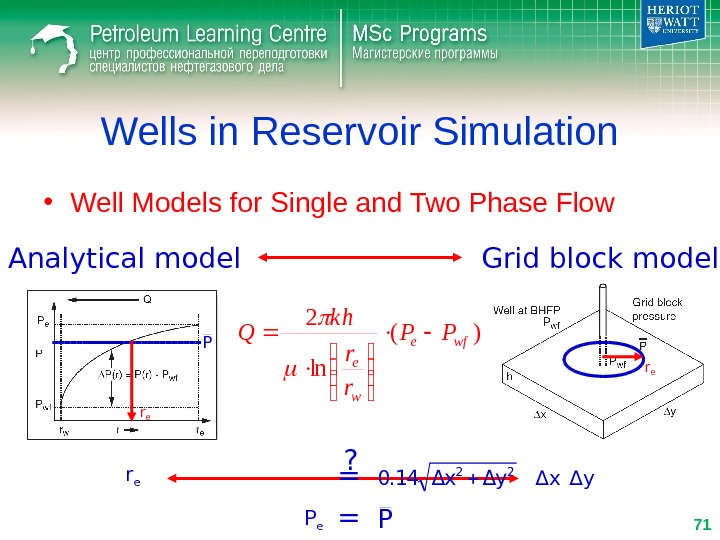
 Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Peaceman Equivalent radius, re Δxre 0. 2 ( Δ x= Δ y) 2 yre 2 x 0. 14 ( Δ x≠ Δ y)
Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Peaceman Equivalent radius, re Δxre 0. 2 ( Δ x= Δ y) 2 yre 2 x 0. 14 ( Δ x≠ Δ y)
 Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Peaceman Equivalent radius, re Δxre 0. 196 Δxre 0. 2 Δxre 0. 433 Δxre 0. 193 Δxre 0.
Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Peaceman Equivalent radius, re Δxre 0. 196 Δxre 0. 2 Δxre 0. 433 Δxre 0. 193 Δxre 0.
 Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Peaceman Equivalent radius, re (k x ≠ k y ) 4 1 2 1 22 y x x y e k k Δy k k Δx k k r 0. 28( Δ x≠ Δ y) k x k y
Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Peaceman Equivalent radius, re (k x ≠ k y ) 4 1 2 1 22 y x x y e k k Δy k k Δx k k r 0. 28( Δ x≠ Δ y) k x k y
 Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow)( ln 2 wfe w e PP r r k h Q Analytical model Grid block model r e Δ x Δ y = ? P r e P e P 22ΔyΔx 0. 14 =
Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow)( ln 2 wfe w e PP r r k h Q Analytical model Grid block model r e Δ x Δ y = ? P r e P e P 22ΔyΔx 0. 14 =
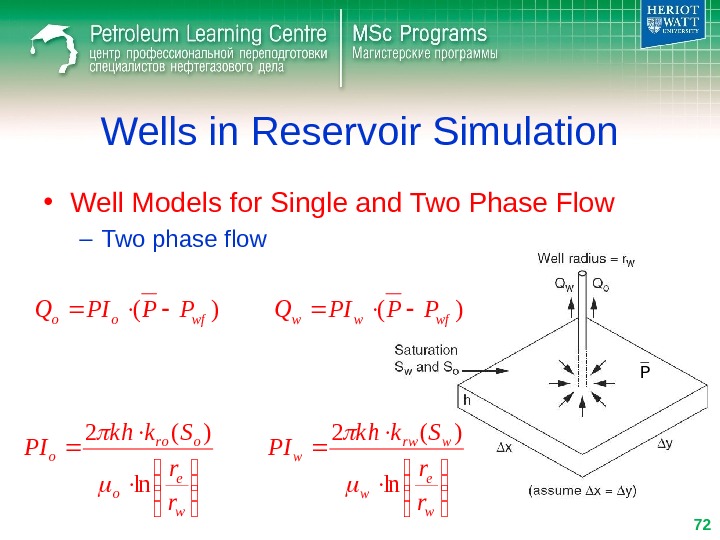
 Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Two phase flow. P )(wfoo. PPPIQ)(wfww. PPPIQ w e o oro o r r Skk h PI ln )(2 w e w wrw w r r Skk h PI ln )(
Wells in Reservoir Simulation • Well Models for Single and Two Phase Flow – Two phase flow. P )(wfoo. PPPIQ)(wfww. PPPIQ w e o oro o r r Skk h PI ln )(2 w e w wrw w r r Skk h PI ln )(
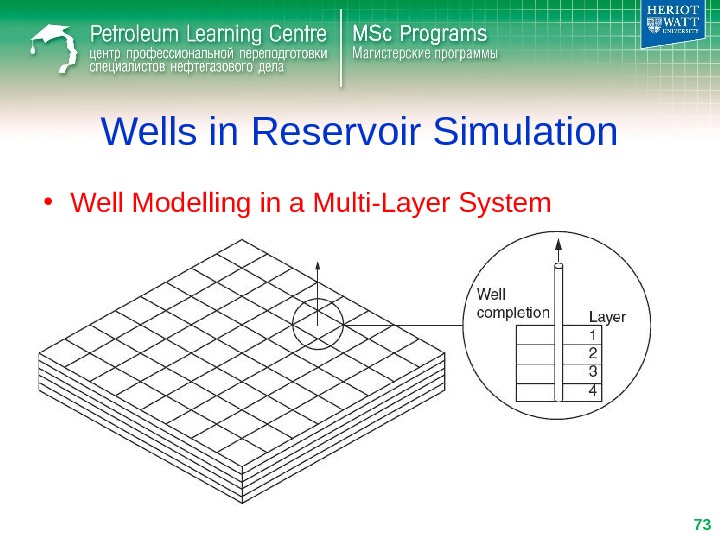
 Wells in Reservoir Simulation • Well Modelling in a Multi-Layer System
Wells in Reservoir Simulation • Well Modelling in a Multi-Layer System
 Wells in Reservoir Simulation • Well Modelling in a Multi-Layer System For each layer (k=1. . 4))(wfkkokok. PPPIQ w ek o koro ok r r Skk h PI ln ))((2 )(wf kkwkwk. PPPIQ w ek w kwrw wk r r Skk h PI ln ))((2 +)()(wfkkwkok. Tk. PPPIPIQ
Wells in Reservoir Simulation • Well Modelling in a Multi-Layer System For each layer (k=1. . 4))(wfkkokok. PPPIQ w ek o koro ok r r Skk h PI ln ))((2 )(wf kkwkwk. PPPIQ w ek w kwrw wk r r Skk h PI ln ))((2 +)()(wfkkwkok. Tk. PPPIPIQ
 Wells in Reservoir Simulation • Well Modelling in a Multi-Layer System For each layer (k=1. . 4))(wfkkokok. PPPIQ )(wf kkwkwk. PPPIQ )()(wfkkwkok. Tk. PPPIPIQ 4 1 )()( k wfkkwkok. TPPPIPIQ Total 4 1 )( k wfkkoko. PPPIQ 4 1 )( k wfkkwkw. PPPIQ For simplicity 4321 wfwf. PPPP
Wells in Reservoir Simulation • Well Modelling in a Multi-Layer System For each layer (k=1. . 4))(wfkkokok. PPPIQ )(wf kkwkwk. PPPIQ )()(wfkkwkok. Tk. PPPIPIQ 4 1 )()( k wfkkwkok. TPPPIPIQ Total 4 1 )( k wfkkoko. PPPIQ 4 1 )( k wfkkwkw. PPPIQ For simplicity 4321 wfwf. PPPP
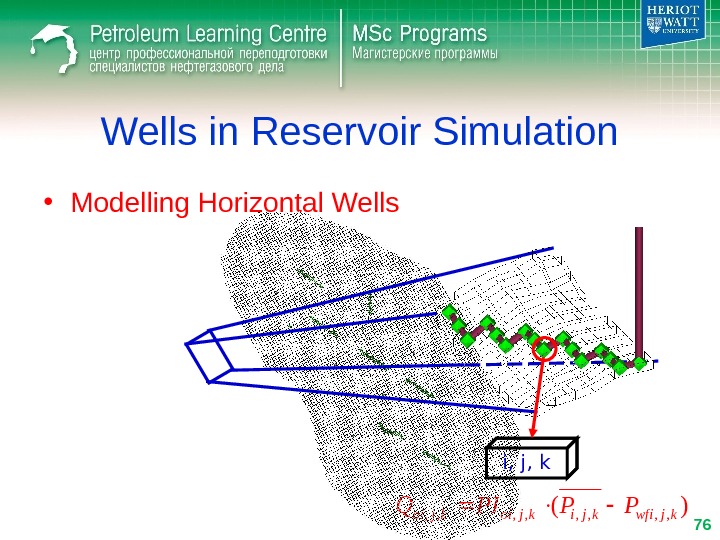
 Wells in Reservoir Simulation • Modelling Horizontal Wells)(, , , , kjwfikjikjoi. PPPIQ i, j, k
Wells in Reservoir Simulation • Modelling Horizontal Wells)(, , , , kjwfikjikjoi. PPPIQ i, j, k
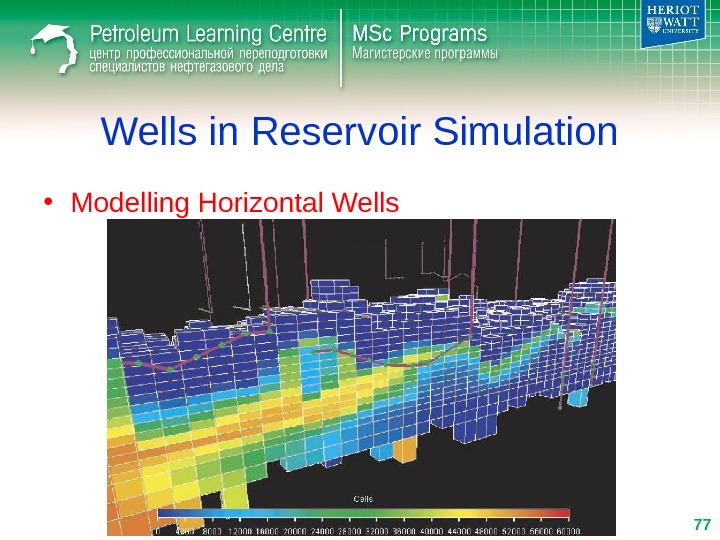
 Wells in Reservoir Simulation • Modelling Horizontal Wells
Wells in Reservoir Simulation • Modelling Horizontal Wells
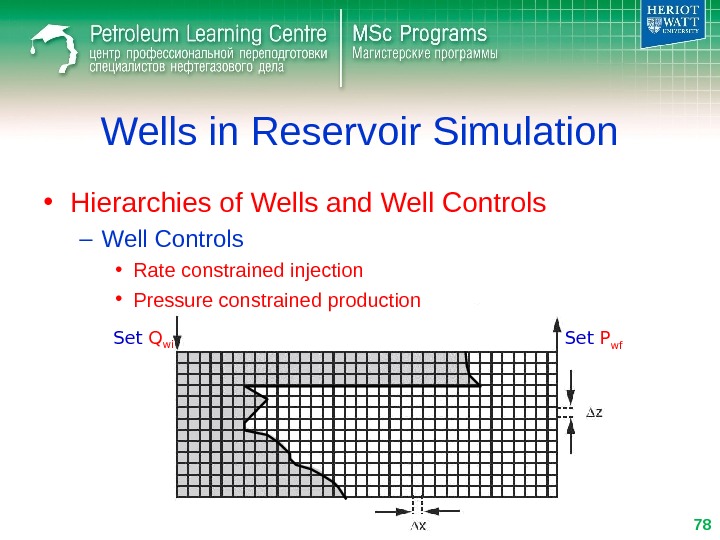
 Wells in Reservoir Simulation • Hierarchies of Wells and Well Controls – Well Controls • Rate constrained injection • Pressure constrained production Set Q wi Set P wf
Wells in Reservoir Simulation • Hierarchies of Wells and Well Controls – Well Controls • Rate constrained injection • Pressure constrained production Set Q wi Set P wf
 Wells in Reservoir Simulation • Hierarchies of Wells and Well Controls – Well Controls • Rate or Pressure constrained production • Voidage replacement (injection) variable Q wi Q op + Q wp Q wi res =Q wi ·B w Q p res =Q op ·B o +Q wp ·B w
Wells in Reservoir Simulation • Hierarchies of Wells and Well Controls – Well Controls • Rate or Pressure constrained production • Voidage replacement (injection) variable Q wi Q op + Q wp Q wi res =Q wi ·B w Q p res =Q op ·B o +Q wp ·B w
 Wells in Reservoir Simulation • Hierarchies of Wells and Well Controls – Well Controls • Rate or Pressure constrained production • Voidage replacement (injection) variable Q wi Q op + Q wp Q wi res =Q wi ·B w Q p res =Q op ·B o +Q wp ·B w. Q wi ·B w =Q op ·B o +Q wp ·B w. Q wi =Q op ·(B o /B w ) +Q wp
Wells in Reservoir Simulation • Hierarchies of Wells and Well Controls – Well Controls • Rate or Pressure constrained production • Voidage replacement (injection) variable Q wi Q op + Q wp Q wi res =Q wi ·B w Q p res =Q op ·B o +Q wp ·B w. Q wi ·B w =Q op ·B o +Q wp ·B w. Q wi =Q op ·(B o /B w ) +Q wp
 Thank you for attention! Reservoir Simulation Gridding and Well Modelling Sergey Kurelenkov
Thank you for attention! Reservoir Simulation Gridding and Well Modelling Sergey Kurelenkov

