Скачать презентацию Research of William Perrizo C S Department NDSU
cf999634122b24f7d3d33668c3fc85ad.ppt
- Количество слайдов: 125
Research of William Perrizo, C. S. Department, NDSU I datamine big data (big data ≡ trillions of rows and, sometimes, thousands of columns (which can complicate data mining trillions of rows). How do I do it? I structure the data table as [compressed] vertical bit columns (called "predicate Trees" or " p. Trees"). I process those p. Trees horizontally (because processing across thousands of column structures is orders of magnitude faster than processing down trillions of row structures. As a result, some tasks that might have taken forever can be done in a humanly acceptable amount of time. What is data mining? Largely it is classification (assigning a class label to a row based on a training table of previously classified rows). Clustering and Association Rule Mining (ARM) are important areas of data mining also, and they are related to classification. The purpose of clustering is usually to create [or improve] a training table. It is also used for anomaly detection, a huge area in data mining. ARM is used to data mine more complex data (relationship matrixes between two entities, not just single entity training tables). Recommenders recommend products to customers based on their previous purchases or rents (or based on their ratings of items)". To make a decision, we typically search our memory for similar situations (near neighbor cases) and base our decision on the decisions we (or an expert) made in those similar cases. We do what worked before (for us or for others). I. e. , we let near neighbor cases vote. But which neighbor vote? "The Magical Number Seven, Plus or Minus Two. . . " Information"[2] is one of the most highly cited papers in psychology cognitive psychologist George A. Miller of Princeton University's Department of Psychology in Psychological Review. It argues that the number of objects an average human can hold in working memory is 7 ± 2 (called Miller's Law). Classification provides a better 7. Some current p. Tree Data Mining research projects 1. Map. Reduce FAUST (FAUST= Functional Analytic Unsupervised and Supervised machine Teaching): Map. Reduce and Hadoop are key-value approaches to organizing and managing Big. Data. In FAUST CLASSIFY we start with a Training TABLE and in FAUST CLUSTER we start with a vector space. 2. p. Tree Text Mining: : I am trying to capturiethe reading sequence, not just the term-frequency matrix (lossless capture) of a text corpus. Preliminary work on the term frequency matrix suggests that attribute selection via simple Standard Deviations really helps (select those columns with high St. D because of their separation potential. =). 3. FAUST CLUSTER/ANOMALASER: This is a method finding anomalies very quickly. 4. Secure p. Tree. Bases: This involves anonymizing the identities of the individual p. Trees and randomly padding them to mask their initial bit positions. 5. FAUST PREDICTOR/CLASSIFIER: This technology is described above. 6. p. Tree Algorithmic Tools: An expanded algorithmic tool set is being developed to include quadratic tools and even higher degree tools. 7. p. Tree Alternative Algorithm Implementation: Implementing p. Tree algorithms in hardware (e. g. , FPGAs) should result in orders of magnitude performance increases? 8. p. Tree O/S Infrastructure: Computers and Operating Systems are designed to do logical operations (AND, OR. . . ) rapidly. Exploit this for p. Tree processing speed. 9. p. Tree Recommenders: This includes, Singular Value Decomposition (SVD) recommenders, p. Tree Near Neighbor Recommenders and p. Tree ARM Recommenders.
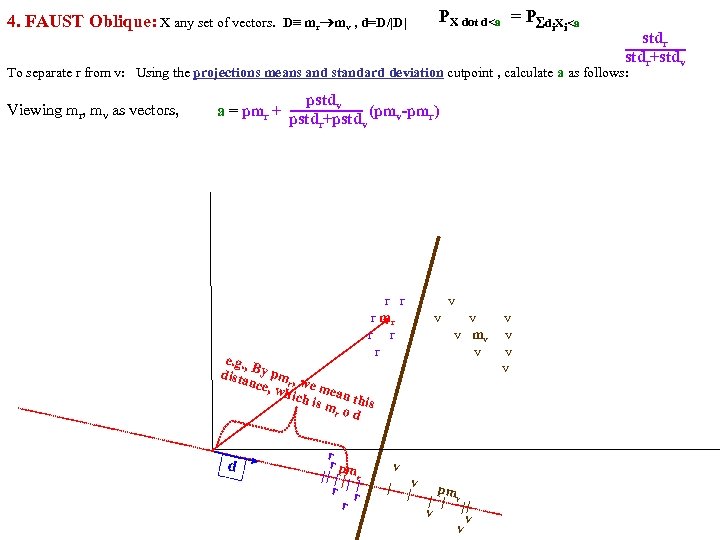
FAUST clustering (the unsupervised part of FAUST) This class of partitioning or clustering methods relies on choosing a functional (mapping of each row in a dim=n table to a real number) which is distance dominated (i. e. , the difference between any two functional values, F(x) and F(y) is always the distance between x and y. The distance dominance of F implies if we find a gap in the F-values, we know that the 2 sets of points mapping to opposite sides of that gap are at least as far apart as the gap width. ). Functionals we've used effectively: The Coordinate Projection Functionals (ej) Check gaps in ej(y) ≡ yj The Square Distance Functional (SD) Check gaps in SDp(y) ≡ (y-p)o(y-p) (parameterized over a p Rn grid). The Dot Product Projection (DPP) Check for gaps in DPPd(y) or DPPpq(y)≡ (y-p)o(p-q)/|p-q| (parameterized over a grid of d=(p-q)/|p-q| Spheren. d The Dot Product Radius (DPR) Check gaps in DPRpq(y) ≡ √ SDp(y) - DPPpq(y)2 The Square Dot Product Radius (SDPR) SDPRpq(y) ≡ SDp(y) - DPPpq(y)2 (easier p. Tree processing) DPP-KM 1. Check gaps in DPPp, d(y) (over grids of p and d? ). 1. 1 Check distances at any sparse extremes. 2. After several rounds of 1, apply k-means to the resulting clusters (when k seems to be determined). DPP-DA 2. Check gaps in DPPp, d(y) (grids of p and d? ) against the density of subcluster. 2. 1 Check distances at sparse extremes against subcluster density. 2. 2 Apply other methods once Dot ceases to be effective. DPP-SD) 3. Check gaps in DPPp, d(y) (over a p-grid and a d-grid) and SDp(y) (over a p-grid). 3. 1 Check sparse ends distance with subcluster density. (DPPpd and SDp share construction steps!) SD-DPP-SDPR) (DPPpq , SDp and SDPRpq share construction steps! SDp(y) ≡ (y-p)o(y-p) = yoy - 2 yop +pop Calc yoy, yop, yoq concurrently? Then constant multiplies DPPpq(y) ≡ (y-p)od=yod-pod= (1/|p-q|)yop - (1/|p-q|)yoq 2*yop, (1/|p-q|)*yop concurrently. Then add | subtract. Calculate DPPpq(y)2. Then subtract it from SDp(y)
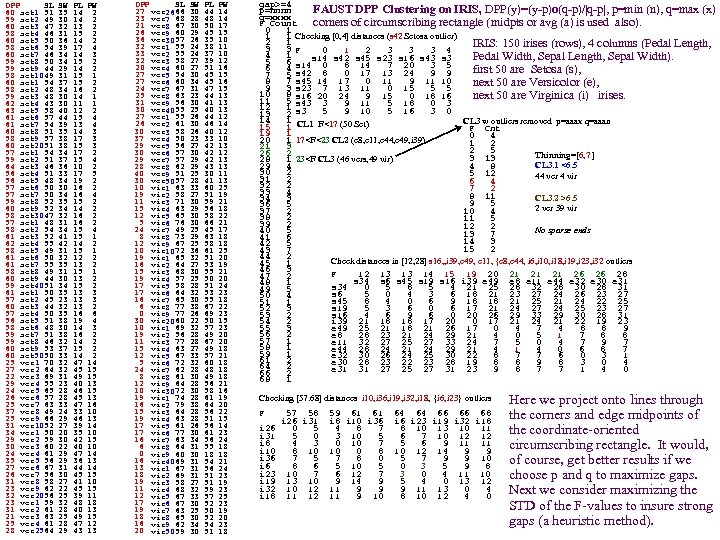DPP SL SW PL PW 60 set 51 35 14 2 1 59 set 49 30 14 2 2 60 set 47 32 13 2 3 58 set 46 31 15 2 4 60 set 50 36 14 2 5 58 set 54 39 17 4 6 60 set 46 34 14 3 7 59 set 50 34 15 2 8 59 set 44 29 14 2 9 58 set 49 31 15 1 10 60 set 54 37 15 2 1 58 set 48 34 16 2 2 59 set 48 30 14 1 3 62 set 43 30 11 1 4 63 set 58 40 12 2 5 61 set 57 44 15 4 6 61 set 54 39 13 4 7 60 set 51 35 14 3 8 58 set 57 38 17 3 9 60 set 51 38 15 3 20 57 set 54 34 17 2 1 59 set 51 37 15 4 2 64 set 46 36 10 2 3 56 set 51 33 17 5 4 56 set 48 34 19 2 5 57 set 50 30 16 2 6 57 set 50 34 16 4 7 59 set 52 35 15 2 8 60 set 52 34 14 2 9 58 set 47 32 16 2 30 57 set 48 31 16 2 1 58 set 54 34 15 4 2 61 set 52 41 15 1 3 62 set 55 42 14 2 4 58 set 49 31 15 1 5 61 set 50 32 12 2 6 61 set 55 35 13 2 7 58 set 49 31 15 1 8 60 set 44 30 13 2 9 59 set 51 34 15 2 40 61 set 50 35 13 3 1 57 set 45 23 13 3 2 60 set 44 32 13 2 3 57 set 50 35 16 6 4 56 set 51 38 19 4 5 58 set 48 30 14 3 6 59 set 51 38 16 2 7 59 set 46 32 14 2 8 60 set 53 37 15 2 9 60 set 50 33 14 2 50 1 25 ver 70 32 47 14 2 27 ver 64 32 45 15 3 22 ver 69 31 49 15 4 29 ver 55 23 40 13 5 24 ver 65 28 46 15 6 26 ver 57 28 45 13 7 25 ver 63 33 47 16 8 37 ver 49 24 33 10 9 25 ver 66 29 46 13 10 31 ver 52 27 39 14 1 34 ver 50 20 35 10 2 29 ver 59 30 42 15 3 30 ver 60 22 40 10 4 24 ver 61 29 47 14 5 35 ver 56 29 36 13 6 27 ver 67 31 44 14 7 26 ver 56 30 45 15 8 31 ver 58 27 41 10 9 23 ver 62 22 45 15 20 32 ver 56 25 39 11 1 23 ver 59 32 48 18 2 31 ver 61 28 40 13 3 21 ver 63 25 49 15 4 25 ver 61 28 47 12 25 28 ver 64 29 43 13 DPP SL SW PL PW 27 ver 66 30 44 14 26 23 ver 68 28 48 14 7 21 ver 67 30 50 17 8 26 ver 60 29 45 15 9 36 ver 57 26 35 10 30 32 ver 55 24 38 11 1 33 ver 55 24 37 10 2 32 ver 58 27 39 12 3 20 ver 60 27 51 16 4 27 ver 54 30 45 15 5 27 ver 60 34 45 16 6 24 ver 67 31 47 15 7 25 ver 63 23 44 13 8 31 ver 56 30 41 13 9 30 ver 55 25 40 13 40 27 ver 55 26 44 12 1 26 ver 61 30 46 14 2 30 ver 58 26 40 12 3 37 ver 50 23 33 10 4 29 ver 56 27 42 13 5 30 ver 57 30 42 12 6 29 ver 57 29 42 13 7 28 ver 62 29 43 13 8 40 ver 51 25 30 11 9 30 ver 57 28 41 13 50 10 vir 63 33 60 25 1 19 vir 58 27 51 19 2 11 vir 71 30 59 21 3 15 vir 63 29 56 18 4 12 vir 65 30 58 22 5 5 vir 76 30 66 21 6 24 vir 49 25 45 17 7 8 vir 73 29 63 18 8 12 vir 67 25 58 18 9 10 vir 72 36 61 25 10 19 vir 65 32 51 20 1 16 vir 64 27 53 19 2 15 vir 68 30 55 21 3 19 vir 57 25 50 20 4 17 vir 58 28 51 24 5 17 vir 64 32 53 23 6 16 vir 65 30 55 18 7 6 vir 77 38 67 22 8 0 vir 77 26 69 23 9 30 vir 60 22 50 15 20 10 vir 69 32 57 23 1 19 vir 56 28 49 20 2 11 vir 77 28 67 20 3 15 vir 63 27 49 18 4 12 vir 67 33 57 21 5 5 vir 72 32 60 18 6 24 vir 62 28 48 18 7 8 vir 61 30 49 18 8 12 vir 64 28 56 21 9 10 vir 72 30 58 16 30 19 vir 74 28 61 19 1 16 vir 79 38 64 20 2 15 vir 64 28 56 22 3 19 vir 63 28 51 15 4 17 vir 61 26 56 14 5 17 vir 77 30 61 23 6 16 vir 63 34 56 24 7 6 vir 64 31 55 18 8 0 vir 60 30 18 18 9 16 vir 69 31 54 21 40 13 vir 67 31 56 24 1 18 vir 69 31 51 23 2 19 vir 58 27 51 19 3 11 vir 68 32 59 23 4 12 vir 67 33 57 25 5 17 vir 67 30 52 23 6 19 vir 63 25 50 19 7 18 vir 65 30 52 20 8 16 vir 62 34 54 23 9 20 vir 59 30 51 18 50 gap>=4 p=nnnn FAUST DPP Clustering on IRIS, DPP(y)=(y-p)o(q-p)/|q-p|, p=min (n), q=max (x) q=xxxx F Count corners of circumscribing rectangle (midpts or avg (a) is used also). 0 1 1 1 Checking [0, 4] distances (s 42 Setosa outlier) 2 1 IRIS: 150 irises (rows), 4 columns (Pedal Length, 3 3 F 0 1 2 3 3 3 4 4 1 s 14 s 42 s 45 s 23 s 16 s 43 s 3 Pedal Width, Sepal Length, Sepal Width). 5 6 s 14 0 8 14 7 20 3 5 6 4 first 50 are Setosa (s), s 42 8 0 17 13 24 9 9 7 5 8 7 s 45 14 17 0 11 9 11 10 next 50 are Versicolor (e), 9 3 s 23 7 13 11 0 15 5 5 10 8 s 16 20 24 9 15 0 18 16 next 50 are Virginica (i) irises. 11 5 s 43 3 9 11 5 18 0 3 12 1 s 3 5 9 10 5 16 3 0 13 2 14 1 CL 1 F<17 (50 Set) CL 3 w outliers removed p=aaax q=aaan 15 1 F Cnt 19 1 0 4 20 1 17
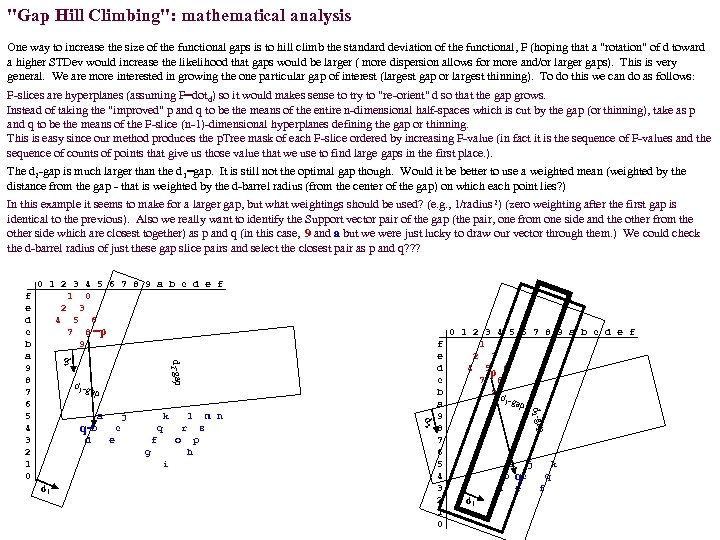
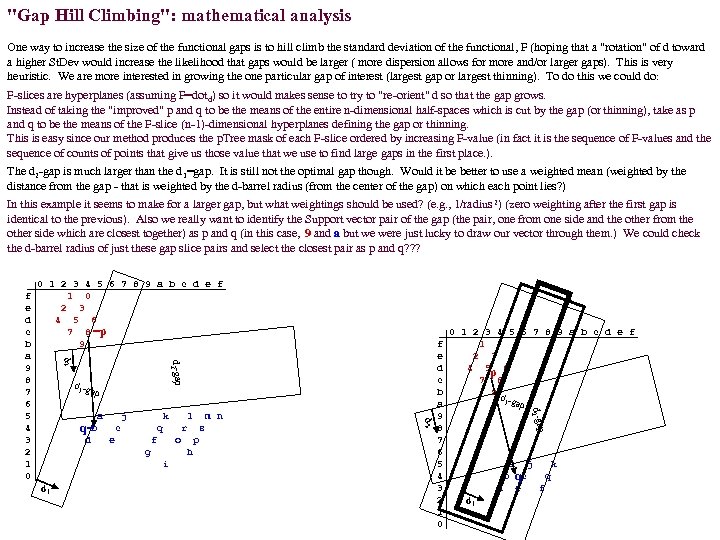"Gap Hill Climbing": mathematical analysis One way to increase the size of the functional gaps is to hill climb the standard deviation of the functional, F (hoping that a "rotation" of d toward a higher St. Dev would increase the likelihood that gaps would be larger ( more dispersion allows for more and/or larger gaps). This is very heuristic. We are more interested in growing the one particular gap of interest (largest gap or largest thinning). To do this we could do: F-slices are hyperplanes (assuming F=dotd) so it would makes sense to try to "re-orient" d so that the gap grows. Instead of taking the "improved" p and q to be the means of the entire n-dimensional half-spaces which is cut by the gap (or thinning), take as p and q to be the means of the F-slice (n-1)-dimensional hyperplanes defining the gap or thinning. This is easy since our method produces the p. Tree mask of each F-slice ordered by increasing F-value (in fact it is the sequence of F-values and the sequence of counts of points that give us those value that we use to find large gaps in the first place. ). The d 2 -gap is much larger than the d 1=gap. It is still not the optimal gap though. Would it be better to use a weighted mean (weighted by the distance from the gap - that is weighted by the d-barrel radius (from the center of the gap) on which each point lies? ) In this example it seems to make for a larger gap, but what weightings should be used? (e. g. , 1/radius 2) (zero weighting after the first gap is identical to the previous). Also we really want to identify the Support vector pair of the gap (the pair, one from one side and the other from the other side which are closest together) as p and q (in this case, 9 and a but we were just lucky to draw our vector through them. ) We could check the d-barrel radius of just these gap slice pairs and select the closest pair as p and q? ? ? 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 0 2 3 4 5 6 7 8 =p 9 d 2 -gap d 2 d 1 -g ap j e m n r f s o g p h i d 1 l q 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 2 3 4 5 p 6 7 8 9 d 1 -gap p d k c f e d c b a 9 8 7 6 5 4 3 2 1 0 d 2 -ga a b q= d 2 f e d c b a 9 8 7 6 5 4 3 2 1 0 a b d d 1 j k qc e q f
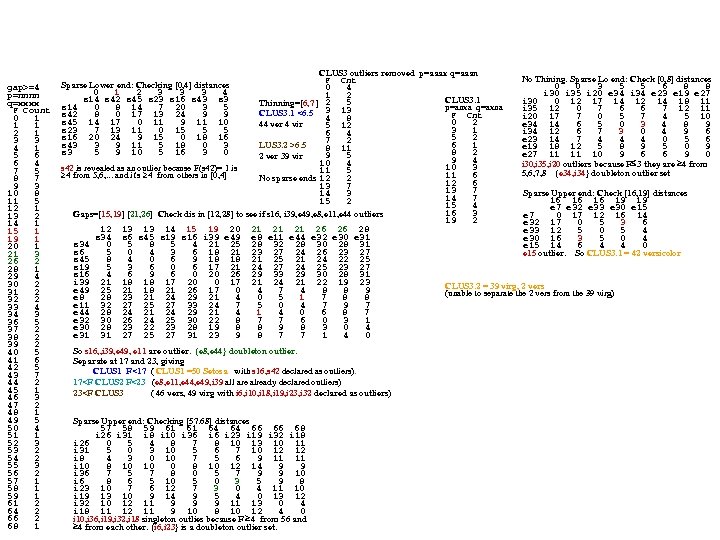gap>=4 p=nnnn q=xxxx F Count 0 1 1 1 2 1 3 3 4 1 5 6 6 4 7 5 8 7 9 3 10 8 11 5 12 1 13 2 14 1 15 1 19 1 20 1 21 3 26 2 28 1 29 4 30 2 31 2 32 2 33 4 34 3 36 5 37 2 38 2 39 2 40 5 41 6 42 5 43 7 44 2 45 1 46 3 47 2 48 1 49 5 50 4 51 1 52 3 53 2 54 2 55 3 56 2 57 1 58 1 59 1 61 2 64 2 66 2 68 1 CLUS 3 outliers removed p=aaax q=aaan No Thining. Sparse Lo end: Check [0, 8] distances F Cnt 0 0 3 5 5 6 8 8 0 4 i 30 i 35 i 20 e 34 i 34 e 23 e 19 e 27 1 2 CLUS 3. 1 i 30 0 12 17 14 12 14 18 11 5 Thinning=[6, 7 ] 2 p=anxa q=axna i 35 12 0 7 6 6 7 12 11 CLUS 3. 1 <6. 5 3 13 F Cnt i 20 17 7 0 5 7 4 5 10 4 8 0 2 e 34 14 6 5 0 3 4 8 9 44 ver 4 vir 5 12 3 1 i 34 12 6 7 3 0 4 9 6 6 4 5 2 e 23 14 7 4 4 4 0 5 6 7 2 6 1 LUS 3. 2 >6. 5 e 19 18 12 5 8 9 5 0 9 8 11 8 2 e 27 11 11 10 9 6 6 9 0 9 5 2 ver 39 vir 9 4 10 4 i 30, i 35, i 20 outliers because F 3 they are 4 from 10 3 s 42 is revealed as an outlier because F(s 42)= 1 is 11 5 5, 6, 7, 8 {e 34, i 34} doubleton outlier set 11 6 4 from 5, 6, . . . and it's 4 from others in [0, 4] No sparse ends 12 2 12 6 13 7 Sparse Upper end: Check [16, 19] distances 14 3 14 7 16 16 16 19 19 15 2 15 4 e 7 e 32 e 33 e 30 e 15 16 3 Gaps=[15, 19] [21, 26] Check dis in [12, 28] to see if s 16, i 39, e 49, e 8, e 11, e 44 outliers e 7 0 17 12 16 14 19 2 e 32 17 0 5 3 6 12 13 13 14 15 19 20 21 21 21 26 26 28 e 33 12 5 0 5 4 s 34 s 6 s 45 s 19 s 16 i 39 e 49 e 8 e 11 e 44 e 32 e 30 e 31 e 30 16 3 5 0 4 s 34 0 5 8 5 4 21 25 28 32 28 30 28 31 e 15 14 6 4 4 0 s 6 5 0 4 3 6 18 21 23 27 24 26 23 27 e 15 outlier. So CLUS 3. 1 = 42 versicolor s 45 8 4 0 6 9 18 18 21 25 21 24 22 25 s 19 5 3 6 0 6 17 21 24 27 24 25 23 27 s 16 4 6 9 6 0 20 26 29 33 29 30 28 31 i 39 21 18 18 17 20 0 17 21 24 21 22 19 23 CLUS 3. 2 = 39 virg, 2 vers e 49 25 21 18 21 26 17 0 4 7 4 8 8 9 (unable to separate the 2 vers from the 39 virg) e 8 28 23 21 24 29 21 4 0 5 1 7 8 8 e 11 32 27 25 27 33 24 7 5 0 4 7 9 7 e 44 28 24 21 24 29 21 4 0 6 8 7 e 32 30 26 24 25 30 22 8 7 7 6 0 3 1 e 30 28 23 22 23 28 19 8 8 9 8 3 0 4 e 31 31 27 25 27 31 23 9 8 7 7 1 4 0 Sparse Lower end: Checking [0, 4] distances 0 1 2 3 3 3 4 s 14 s 42 s 45 s 23 s 16 s 43 s 14 0 8 14 7 20 3 5 s 42 8 0 17 13 24 9 9 s 45 14 17 0 11 9 11 10 s 23 7 13 11 0 15 5 5 s 16 20 24 9 15 0 18 16 s 43 3 9 11 5 18 0 3 s 3 5 9 10 5 16 3 0 So s 16, , i 39, e 49, e 11 are outlier. {e 8, e 44} doubleton outlier. Separate at 17 and 23, giving CLUS 1 F<17 ( CLUS 1 =50 Setosa with s 16, s 42 declared as outliers). 17
![CLUS 1 Sparse low end (check [0, 9] p=nxnn 0 2 4 6 6](https://present5.com/presentation/cf999634122b24f7d3d33668c3fc85ad/image-6.jpg "CLUS 1 Sparse low end (check [0, 9] p=nxnn 0 2 4 6 6")
CLUS 1 Sparse low end (check [0, 9] p=nxnn 0 2 4 6 6 9 10 q=xnxx i 23 i 6 i 36 i 8 i 31 i 3 i 26 0 1 2 3 3 4 4 4 4 5 6 6 6 6 7 7 i 23 0 3 7 6 7 10 10 Dotgp>=4 2 1 i 18 i 19 i 10 i 37 i 5 i 6 i 23 i 32 i 44 i 45 i 49 i 25 i 8 i 15 i 41 i 21 i 33 i 29 i 4 i 3 i 16 i 6 3 0 5 5 6 9 8 p=xnnn 4 1 i 1 0 17 18 10 4 5 15 17 18 6 5 6 6 13 11 6 7 7 8 9 9 7 i 36 7 5 0 7 5 7 7 q=nxxx 6 2 i 18 17 0 12 9 18 17 8 10 4 13 15 20 15 11 27 17 14 20 20 20 13 20 i 8 6 5 7 0 3 5 4 0 1 9 1 i 19 18 12 0 14 21 17 5 4 13 15 17 23 17 9 26 17 16 19 19 20 12 21 i 31 7 6 5 3 0 5 5 1 1 10 1 i 10 10 9 14 0 11 10 10 12 9 6 7 13 8 10 19 9 7 13 13 14 8 12 i 3 10 9 7 5 5 0 4 2 1 11 2 i 37 4 18 21 11 0 5 17 19 19 6 4 2 5 14 9 5 6 6 7 8 10 4 i 26 10 8 7 4 5 4 0 3 2 12 2 i 5 5 17 17 10 5 0 14 15 17 4 5 6 4 10 10 4 5 3 3 5 6 6 i 3, i 26, i 36 >=4 singleton outliers 4 7 13 3 i 6 15 8 5 10 17 14 0 3 9 11 14 19 13 5 24 14 12 16 16 17 9 18 {i 23, i 6}, {i 8, i 31} doubleton ols 5 1 14 3 i 23 17 10 4 12 19 15 3 0 11 13 16 21 15 6 25 16 14 17 17 18 10 20 6 7 15 2 i 32 18 4 13 9 19 17 9 11 0 14 16 20 15 11 27 17 14 20 20 20 12 20 7 5 16 2 i 44 6 13 15 6 6 4 11 13 14 0 3 8 3 9 13 3 2 6 7 8 4 7 8 9 17 4 i 45 5 15 17 7 4 5 14 16 16 3 0 6 4 12 12 2 3 7 7 9 7 5 9 3 18 3 i 49 6 20 23 13 2 6 19 21 20 8 6 0 6 16 8 7 7 7 11 3 10 7 19 3 i 25 6 15 17 8 5 4 13 15 15 3 4 6 0 10 12 4 3 6 6 6 5 5 11 3 20 2 i 8 13 11 9 10 14 10 5 6 11 9 12 16 10 0 20 11 9 12 12 12 5 15 12 5 21 5 i 15 11 27 26 19 9 10 24 25 27 13 12 8 12 20 0 11 13 8 8 9 16 8 13 4 22 6 i 41 6 17 17 9 5 4 14 16 17 3 2 6 4 11 11 0 3 5 5 7 6 4 14 5 23 5 i 21 7 14 16 7 6 5 12 14 14 2 3 8 3 9 13 3 0 7 7 8 4 6 15 4 Sparse hi end (checking [34, 43] 24 2 i 33 7 20 19 13 6 3 16 17 20 6 7 7 6 12 8 5 7 0 1 4 8 5 16 8 34 35 36 36 37 37 39 41 42 43 25 7 i 29 8 20 19 13 7 3 16 17 20 7 7 7 6 12 8 5 7 1 0 3 8 5 17 4 e 20 e 31 e 10 e 32 e 15 e 30 e 11 e 44 e 8 e 49 26 3 i 4 9 20 20 14 8 5 17 18 20 8 9 7 6 12 9 7 8 4 3 0 9 7 18 7 e 20 0 2 5 3 5 4 9 9 9 10 27 2 i 3 9 13 12 8 10 6 9 10 12 4 7 11 5 5 16 6 4 8 8 9 0 10 19 3 e 31 2 0 5 1 6 4 7 7 8 9 28 2 i 16 7 20 21 12 4 6 18 20 20 7 5 3 5 15 8 4 6 5 5 7 10 0 20 5 e 10 5 5 0 6 5 8 9 8 8 10 29 1 i 26 11 11 13 8 12 9 8 10 10 6 9 13 7 4 18 9 7 11 10 10 4 12 21 1 e 32 3 1 6 0 6 3 7 6 7 8 30 3 i 36 14 10 9 8 15 12 5 7 9 9 11 17 11 7 22 11 9 14 14 16 7 15 22 4 e 15 5 6 0 4 11 9 10 9 31 3 i 38 9 19 20 13 7 5 17 18 19 8 8 6 5 12 10 7 7 5 4 2 9 5 23 1 e 30 4 4 8 3 4 0 9 8 8 8 32 7 i 1, i 18, i 19, i 10, i 37, i 32 >=4 outliers 24 1 e 11 9 7 11 9 0 4 5 7 33 4 gap: (24, 31) CLUS 1<27. 5 (50 versi, 49 virg) CLUS 2>27. 5 (50 set, 1 virg) 31 2 e 44 9 7 8 6 9 8 4 0 1 4 34 1 33 2 e 8 9 8 8 7 10 8 5 1 0 4 35 1 34 12 Sparse hi end (checking [38, 39] e 49 10 8 9 8 7 4 4 0 36 2 35 8 38 38 39 39 e 30, e 49, ei 15, e 11 >=4 singleton ols 37 2 36 17 s 42 s 36 s 37 s 1 {e 44, e 8} doubleton ols 39 1 Thinning (8, 13) 37 6 s 42 0 10 16 21 41 1 CLUS 1 Split in middle=10. 5 38 2 s 36 10 0 6 11 42 1 Dotgp>=4 CLUS_1. 1<10. 5 (21 virg, 2 ver) 39 2 s 37 16 6 0 6 43 1 p=nnnn CLUS_1. 2>10. 5 (12 virg, 42 ver) s 15 21 11 6 0 q=xxxx Clus 1 s 37, s 1 outliers 0 1 p=nnxn Sparse hi end (checking [10, 13] Thinning (7, 9) 1 2 q=xxnx 10 10 11 11 13 13 Split in middle=7. 5 2 2 0 2 CLUS 1 e 34 i 2 i 14 i 43 e 41 i 20 i 7 i 35 CLUS_1. 2. 1 < 7. 5 (10 virg, 4 ver) 3 1 1 1 Dotgp>=4 CLUS 1. 2 CLUS_1. 2. 2 > 7. 5 ( 1 virg, 38 ver) e 34 0 4 5 4 10 5 13 6 4 2 2 5 p=nnnx Dotgp>=4 i 15 gap>=4 outlier at F=0 i 2 4 0 3 0 10 7 11 8 5 1 3 8 q=xxxn p=aaan hi end gap outlier i 30 i 14 5 3 0 3 10 7 10 9 6 6 4 9 CLUS 1. 2. 1 0 1 q=aaax i 43 4 0 3 0 10 7 11 8 7 2 5 6 Dotgp>=4 4 1 CLUS 1. 2. 1 0 1 e 41 10 10 0 9 8 14 8 3 6 9 p=anaa 5 3 Dotgp>=4 4 4 i 20 5 7 7 7 9 0 13 7 9 1 7 14 q=axaa 6 5 p=aana 5 3 i 7 13 11 10 11 8 13 0 17 10 2 8 11 0 1 7 4 q=aaxa 6 3 i 35 6 8 9 8 14 7 17 0 11 2 9 7 1 1 8 3 0 5 7 4 i 7, i 35 >=4 singleton outliers 12 2 10 4 2 1 9 6 1 2 8 1 13 6 11 2 4 2 10 7 2 3 9 5 14 6 13 2 6 3 11 3 3 2 10 7 15 7 7 4 12 4 4 1 11 3 16 2 C. 2. 1 0 0 1 2 3 3 4 4 5 5 6 7 9 2 13 8 6 1 12 5 i 24 e 7 i 34 i 47 i 28 e 34 e 36 e 21 i 50 i 2 i 43 i 14 i 22 17 2 14 4 13 3 i 24 0 7 4 2 2 4 4 9 6 5 5 5 7 7 18 3 15 4 14 6 e 7 7 0 6 9 6 5 8 4 5 7 9 9 11 10 19 3 CLUS 1. 2. 1 16 3 i 34 4 6 0 5 4 5 3 9 7 5 6 6 8 9 15 1 20 2 p=naaa 17 8 i 47 2 9 5 0 4 6 5 11 8 7 5 5 6 8 16 4 21 2 q=xaaa i 27 2 6 4 4 0 2 4 7 5 5 6 6 18 5 17 1 22 3 0 4 i 28 4 5 5 6 2 0 4 6 3 3 5 5 7 6 19 3 18 1 e 34 4 8 3 5 4 4 0 9 6 4 4 4 5 6 23 4 1 1 20 1 19 2 e 36 9 4 9 11 7 6 9 0 4 8 10 10 11 9 24 2 2 1 21 1 e 21 6 5 7 8 5 3 6 4 0 4 6 6 8 5 25 1 3 2 22 3 i 50 5 7 5 3 4 8 4 0 3 3 6 5 26 2 4 2 23 1 i 2 5 9 6 5 5 5 4 10 6 3 0 0 3 3 27 3 5 2 i 43 5 9 6 5 5 5 4 10 6 3 0 0 3 3 28 1 6 1 i 14 7 11 8 6 6 7 5 11 8 6 3 3 0 3 i 22 7 10 9 8 6 6 6 9 5 5 3 3 3 0 29 1 7 1 DPP (other corners) Check Dotp, d(y) gaps>=4 Check sparse ends. Sparse low end (checking [0, 7]
HILL CLIMBING GAP WIDTH Check Dotp, d(y) for thinnings. Use AVG of each side of the thinning for p, q. redo. Dot F p=aaan q=aaax 0 3 1 3 2 8 3 3 4 6 5 6 6 5 7 12 8 2 9 4 10 12 11 8 12 13 13 5 14 3 15 7 19 1 20 1 21 7 22 7 23 28 24 6 Cut=8 CLUS_1. 1<8 (45 Virg, 1 Vers) 8
"Gap Hill Climbing": mathematical analysis One way to increase the size of the functional gaps is to hill climb the standard deviation of the functional, F (hoping that a "rotation" of d toward a higher STDev would increase the likelihood that gaps would be larger ( more dispersion allows for more and/or larger gaps). This is very general. We are more interested in growing the one particular gap of interest (largest gap or largest thinning). To do this we can do as follows: F-slices are hyperplanes (assuming F=dotd) so it would makes sense to try to "re-orient" d so that the gap grows. Instead of taking the "improved" p and q to be the means of the entire n-dimensional half-spaces which is cut by the gap (or thinning), take as p and q to be the means of the F-slice (n-1)-dimensional hyperplanes defining the gap or thinning. This is easy since our method produces the p. Tree mask of each F-slice ordered by increasing F-value (in fact it is the sequence of F-values and the sequence of counts of points that give us those value that we use to find large gaps in the first place. ). The d 2 -gap is much larger than the d 1=gap. It is still not the optimal gap though. Would it be better to use a weighted mean (weighted by the distance from the gap - that is weighted by the d-barrel radius (from the center of the gap) on which each point lies? ) In this example it seems to make for a larger gap, but what weightings should be used? (e. g. , 1/radius 2) (zero weighting after the first gap is identical to the previous). Also we really want to identify the Support vector pair of the gap (the pair, one from one side and the other from the other side which are closest together) as p and q (in this case, 9 and a but we were just lucky to draw our vector through them. ) We could check the d-barrel radius of just these gap slice pairs and select the closest pair as p and q? ? ? 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 0 2 3 4 5 6 7 8 =p 9 d 2 -gap d 2 d 1 -g ap j e m n r f s o g p h i d 1 l q 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 2 3 4 5 p 6 7 8 9 d 1 -gap p d k c f e d c b a 9 8 7 6 5 4 3 2 1 0 d 2 -ga a b q= d 2 f e d c b a 9 8 7 6 5 4 3 2 1 0 a b d d 1 j k qc e q f
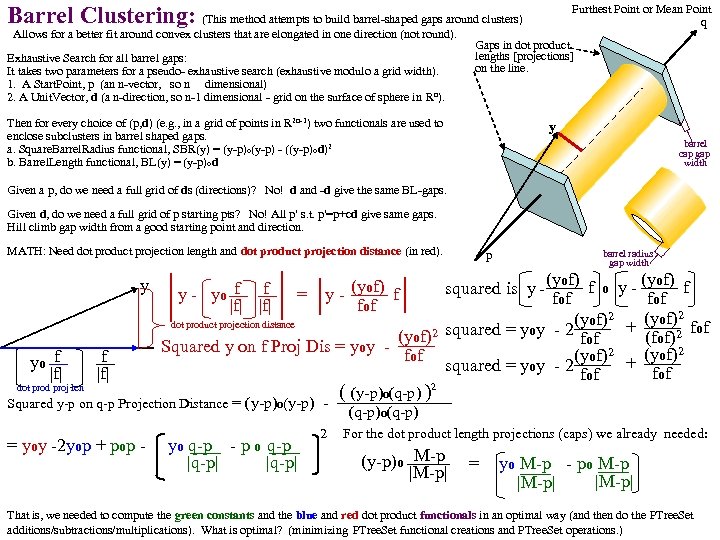Barrel Clustering: (This method attempts to build barrel-shaped gaps around clusters) Allows for a better fit around convex clusters that are elongated in one direction (not round). Exhaustive Search for all barrel gaps: It takes two parameters for a pseudo- exhaustive search (exhaustive modulo a grid width). 1. A Start. Point, p (an n-vector, so n dimensional) 2. A Unit. Vector, d (a n-direction, so n-1 dimensional - grid on the surface of sphere in Rn). Furthest Point or Mean Point q Gaps in dot product lengths [projections] on the line. Then for every choice of (p, d) (e. g. , in a grid of points in R 2 n-1) two functionals are used to enclose subclusters in barrel shaped gaps. a. Square. Barrel. Radius functional, SBR(y) = (y-p)o(y-p) - ((y-p)od)2 b. Barrel. Length functional, BL(y) = (y-p)od y barrel cap gap width Given a p, do we need a full grid of ds (directions)? No! d and -d give the same BL-gaps. Given d, do we need a full grid of p starting pts? No! All p' s. t. p'=p+cd give same gaps. Hill climb gap width from a good starting point and direction. MATH: Need dot product projection length and dot product projection distance (in red). y yo f |f| p barrel radius gap width (yof) f o y - of) f (y squared is y - fof (yof)2 + fof dot product projection distance (yof)2 squared = yoy - 2 fof (fof)2 Squared y on f Proj Dis = yoy f (yof)2 + fof squared = yoy - 2 fof y - yo f f |f| (y = y - of) f fof ( (y-p)o(q-p) )2 Squared y-p on q-p Projection Distance = (y-p)o(y-p) (q-p)o(q-p) dot prod proj len 1 st = yoy -2 yop + pop - ( yo(q-p) - p o(q-p |q-p| 2 For the dot product length projections (caps) we already needed: (y-p)o M-p = ( yo(M-p) - po M-p ) |M-p| That is, we needed to compute the green constants and the blue and red dot product functionals in an optimal way (and then do the PTree. Set additions/subtractions/multiplications). What is optimal? (minimizing PTree. Set functional creations and PTree. Set operations. )
4 functionals in the dot product group of gap clusterers on a Vector. Space subset, Y (y Y): 1. SLp(y) = (y-p)o(y-p), p a fixed vector. Square Length functional primarily for outlier identification and densities. 2. Dotd(y) = yod, (d is a unit vector) the Dot-product functional. Using d=q-p/|q-p| and y-p y y y - (yod)d = projection. Squaring its y - (yod)d Dotp, q(y) = (y-p)o(q-p)/|q-p| 2 length: (y-yodd)o(y-yodd)=yoy-(yod) so again yoy - (yod)2 = squared proj d yod projection yod projection (neg) d 3. SPDd(y) = yoy - (yod)2 (d a unit vector) is the Square Projection Distance functional ( (y-p)o(q-p) )2 E. g. , if d ≡ (q-p)/|q-p|, d = unit vector from vector p to vector q, then SPD(y)= (y-p)o(y-p) (q-p)o(q-p) But to avoid creating an entirely new Vector. PTree. Set(Y-p) 2 for the space (with origin shifted to p), we think it useful q-p to alter the expression to : SPDpq(y) = yoy -2 yop + pop - yo - po |q-p| where we might: q-p 1 st compute the constant vector 2 nd the Scalar. PTree. Set yo q-p |q-p| q-p po 3 rd the constant |q-p| 5 th the SPTree. Set yo q-p - po q-p |q-p| 7 th the SPTree. Sets yoy, yop |q-p| 4 th the SPTree. Set yo q-p - po q-p |q-p| 6 th the constant pop q-p - po |M-p| 8 th the SPTree. Set= yoy -2 yop + pop - yo |M-p| Is it better to leave all the additions and subtractions for one mega-step at the end? Other efficiency thoughts? We note that Dot(y)=yod shares many construction steps with SPD. (y-p)o q-p |q-p| = yo q-p - po |q-p| 4. CAd(y) = yod/|y|, (d unit vector) the Cone Angle functional. Using d=q-p/|q-p| and y=x-p CAp, q(y) = (y-p)od/|y-p| SCAp, q(y) = (y-p)od 2/|y-p|2 = (y-p)od 2/(y-p)o(y-p), Squared Cone Angle functional 2
SPD p 64 29 50 17 q 61 29 45 14 e 14 V Ct 1 6 2 4 3 8 4 4 5 10 6 2 7 2 8 2 9 7 10 2 11 2 12 2 13 1 15 2 17 1 18 4 19 2 20 4 22 1 24 1 25 1 26 1 29 1 31 2 32 2 33 3 37 2 i 15 i 36 92 1 i 32 SPD p 54 22 39 10 q 70 34 51 18 V Ct 2 8 3 10 4 10 5 10 6 5 thin gap 7 10 8 6 9 8 10 6 11 1 masking V>6: Total_e 37 2 Masked_e Total_i 37 29 Masked_i However I cheated a bit. I used p=Min. Vect(e) and q=Max. Vect(e) which makes it somewhat supervised. START OVER WITH THE FULL 150 ---------> SPD on CLUS 1 p 64 29 50 17 p 50 20 35 10 e 11 q 61 29 45 14 e 14 q 58 31 37 12 =MN V Ct 2 10 2 3 3 12 mask: V<8. 5 3 4 mask: V<12. 5 4 12 CTs 50 0 SMs 4 5 5 SMe 5 12 CTe 50 50 SMe 5 7 24 SMi 6 8 CTi 50 24 SMi 6 2 CLUS 1. 1 7 11 CLUS 1 7 2 8 9 8 6 9 5 mask: 8. 5
SPD p 58 44 69 25 axxx q 58 30 37 11 aaaa V Ct. 2 1 3 5 4 6 mask: V<11. 5 5 6 0 SM setosa 6 8 46 SM versicolor 7 6 24 SM virginica 8 8 CLUS 1 9 15 10 7 11 8 12 13 13 8 mask: V>11. 5 14 14 50 SM setosa 4 SM versicolor 15 9 16 13 26 SM virginica CLUS 2 17 6 18 4 19 4 20 3 21 4 23 1 25 1 SPD on CLUS 1 69 28 46 25 C 11 xaax 60 28 46 15 C 11 aaaa V Ct 1 2 2 3 3 4 4 8 5 8 6 14 7 8 8 4 9 5 10 6 11 1 12 3 14 1 15 2 17 1 no thins SPD on CLUS 1 p 60 34 60 25 C 1 US 1 axxx q 60 28 46 15 C 1 US 1 aaaa V Ct. 1 3 2 5 3 9 4 13 5 18 6 12 7 4 8 1 9 2 11 3 no thinnings SPD on CLUS 1 p 69 28 60 25 C 1 US 1 xaxx q 60 28 46 15 C 1 US 1 aaaa V Ct. 1 4 mask: V<3. 5 2 13 14 SM versi 3 7 10 SM virgi CL 1. 1? 4 19 mask: V>3. 5 5 9 0 SM setosa 6 7 32 SM versi 7 9 14 SM virgi 8 2 CLUS 1. 2? SPD on CLUS 2 p 56 44 69 25 C 1 US 2 axxx q 56 32 29 9 C 1 US 2 aaaa V Ct. 6 2 7 2 mask: V<13. 5 8 6 44 SM setosa 9 13 0 SM versicolor 10 7 02 SM virginica 11 7 CLUS 2. 1 12 4 13 5 14 11 15 9 mask: 100>V>13. 5 16 2 6 SM setosa 18 4 4 21 2 24 SM versicolor SM virginica 22 1 CLUS 2. 2 23 3 25 1 26 1 SPD on CLUS 1 69 28 60 15 C 11 xaxa 60 28 46 15 C 11 aaaa V Ct 1 2 2 3 3 12 4 12 5 10 6 15 7 7 8 4 9 1 10 2 11 1 12 1 no thins SPD on CLUS 1 p 69 34 60 15 C 1 US 1 xxxa q 60 28 46 15 C 1 US 1 aaaa V Ct. 1 1 2 3 3 10 4 15 5 16 6 12 7 7 8 3 9 1 10 1 11 1 no thinnings SPD on CLUS 1 p 60 34 46 25 C 1 US 1 axax SPD on CLUS 1 q 60 28 46 15 C 1 US 1 aaaa p 60 34 60 15 C 1 US 1 axxa V Ct. q 60 28 46 15 C 1 US 1 aaaa 1 1 V Ct. 2 3 1 1 3 4 mask: V<9. 5 2 2 4 2 3 6 5 12 37 SM vers 4 9 6 13 16 SM virg CL 1. 1? 5 12 7 9 8 7 6 17 9 2 7 8 10 7 mask: V>9. 5 8 6 11 4 9 SM vers 9 5 13 2 8 SM virg CL 1. 2? 10 1 14 1 11 1 17 2 12 2 no thinnings 18 1 C 11 axaa C 11 aaaa SPD on C 11 xaaa C 11 aaxa C 11 aaax V Ct C 11 aaaa 1 2 mask: V<5. 5 V Ct 2 2 16 ver 1 2 1 3 1 2 3 2 2 4 3 vir. CL 1. 1? 2 1 2 3 4 10 3 5 3 3 3 6 4 9 5 3 4 4 5 10 4 12 5 12 6 13 6 9 6 15 5 11 7 8 mask: V>5. 5 7 4 7 5 6 9 8 7 30 ver 8 5 8 6 7 11 9 4 21 vir. CL 1. 1? 9 4 9 2 8 5 10 3 10 7 10 6 9 5 11 6 11 4 11 3 10 1 12 2 12 1 13 1 11 3 13 2 14 1 13 2 14 2 15 1 17 2 15 2 17 1 18 1 17 2 18 1 19 1 SPD on CLUS 1 p 60 28 60 25 C 11 aaxx q 60 28 46 15 C 11 aaaa V Ct. 1 1 2 7 3 10 4 13 5 13 6 13 7 6 8 2 9 2 11 1 12 2 no thinnings SPD on CLUS 1 69 28 46 25 C 11 xxaa 60 28 46 15 C 11 aaaa V Ct 1 1 mask: V<5. 5 2 4 26 ver 3 6 4 vir CL 1. 1? 4 9 5 10 6 7 mask: V>5. 5 7 9 20 ver 8 5 20 vir CL 1. 1? 9 3 10 4 11 2 12 4 13 1 14 3 17 2 SPD on CLUS 1 p 69 34 46 25 C 1 US 1 xxax q 60 28 46 15 C 1 US 1 aaaa V Ct. 1 1 2 4 3 3 4 9 5 9 6 14 7 9 8 4 9 6 10 3 11 3 12 1 14 2 15 1 16 1 no thinnings
x=s 15 58 40 12 2 (58=avg(y 1) ) V Ct 0 3 s 15, s 17, s 34 1 12 s 6, 11, 16, 19, 20, 22, 28, 32, 3337, 49 2 12 s 1, 10 13, 18, 21, 27, 29, 40, 41, 44, 45, 50 3 7 s 2, 12, 23, 24, 35, 36, 38 4 10 s 2, 3, 7, 13, 25, 26, 30, 31, 46, 48 5 2 s 4, s 43 6 2 s 9, s 39 7 1 s 14 8 1 i 39 9 1 s 32 ^^all 50 setosa + i 39 14 1 e 49 16 2 17 2 19 1 1. (y-p)o(y-p) remove edge 20 2 outliers ( thr>2*50) 21 5 2. lthin gaps in SPD: d, 22 4 from an edge point to MN. 23 3 24 4 3 For each thin PL, do len 25 1 gap anal of pts in " tube". 27 8 28 2 29 2 30 4 31 1 32 4 34 2 35 2 36 2 37 3 38 2 39 2 40 4 41 1 43 2 44 4 45 2 46 1 47 2 48 1 50 4 52 2 53 2 54 2 56 2 57 1 58 1 i 1 62 1 i 31 vv 9 virginica 63 1 i 10 64 1 i 8 66 1 i 36 69 1 i 32 74 1 i 16 76 1 i 18 77 1 i 23 85 1 i 19 But here I mistakenly used the mean rather than the max corner. So I will redo - but note the high level of cluster and outlier revelation? ? ? i 18 77 38 67 22 p i 32 79 38 64 20 p i 19 77 26 69 23 p max 79 38 69 25 max 79 44 69 25 V Ct 0 2 1 2 2 6 1 1 2 2 3 3 2 3 3 5 4 4 3 3 4 3 5 4 4 4 5 3 6 2 5 2 6 4 7 6 6 6 7 4 8 9 7 3 8 7 9 2 8 5 9 2 10 2 9 4 10 3 11 2 10 4 11 1 12 5 11 2 12 4 13 7 12 3 13 5 14 2 13 4 14 4 15 6 14 6 15 7 95 remaining versicolor 16 2 15 4 16 2 and virginica=Sub. Clus 1. 17 5 16 1 17 5 19 3 17 7 18 3 Continue outlier id rounds 20 2 18 2 19 1 on SC 1 (max. SL, max. SW, 22 3 19 3 20 1 max PW) then do "capped 23 2 20 2 21 4 tube" (further subclusters. ) 24 3 22 2 23 2 25 2 23 1 24 2 26 1 24 2 25 4 27 1 25 4 26 1 e 13 i 7 e 40 e 4 e 10 F 28 1 26 4 27 2 e 13 0 14 7 6 10 28 29 3 27 1 28 1 i 7 14 0 9 9 8 29 30 1 28 2 29 2 e 40 7 9 0 2 4 29 e 32 e 11 e 8 e 44 e 49 31 2 29 2 30 1 e 4 6 9 2 0 5 30 e 32 0 7 7 6 8 32 1 e 32 30 1 32 1 e 10 10 8 4 5 0 32 e 11 7 0 5 4 7 42 1 e 11 32 2 e 8 7 5 0 1 4 43 2 e 8, 44 33 1 {e 4, e 40} form a doubleton outlier set e 44 6 4 1 0 4 44 1 e 49 34 1 i 7 and e 10 are singleton outliers e 49 8 7 4 4 0 51 1 i 39 35 1 60 1 No new outliers reviealed 61 1 SPD(y) =(y-p)o(y-p)-(y-p)od 2 d: mn-mx 62 1 V Ct 63 1 Next slide 64 1 65 1 i 1 63 33 60 25 p 66 1 max 79 38 69 25 67 3 V Ct 68 4 0 2 69 4 1 10 45 remaining setosa. 70 3 2 11 This is Sub. Cluster 2 71 3 3 6 (may have additional 72 4 4 15 outliers or sub 73 2 5 4 subclusters but we 74 5 6 8 will not analyse 75 1 7 9 further (would be 76 2 8 4 done in practice tho 77 1 9 5 78 3 10 2 s 3 s 9 s 39 s 43 s 42 s 23 79 1 11 7 s 3 0 4 4 3 9 5 80 1 s 3 e 13 e 20 e 15 e 31 e 32 e 30 F 13 4 s 9 4 0 1 3 6 8 83 1 s 9 e 13 0 5 9 6 6 7 15 14 2 s 39 4 1 0 2 7 7 84 2 s 39, 43 s 43 3 3 2 0 9 5 e 20 5 2 3 4 15 15 2 85 1 s 42 e 15 9 5 0 6 6 4 16 16 1 s 42 9 6 7 9 0 13 87 1 s 23 e 31 6 2 6 0 1 4 17 17 1 s 23 5 8 7 5 13 0 91 1 s 14 e 32 6 3 6 1 0 3 18 18 1 e 30 7 4 4 4 3 0 19 19 1 2 actual gap-ouliers, checking distances reveals e 30, e 15 outliers 4 e-outlier (versicolor), 5 s-outliers (setosa). e 20, e 31, e 32 form SC 12 Declared tripleton outlier set? (But they are not singleton outliers. )
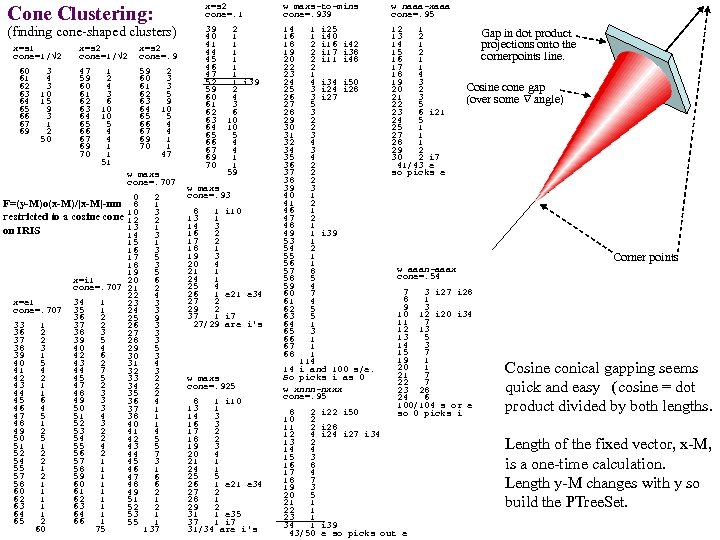Cone Clustering: (finding cone-shaped clusters) x=s 1 cone=1/√ 2 x=s 2 cone=. 9 60 3 61 4 62 3 63 10 64 15 65 9 66 3 67 1 69 2 50 47 1 59 2 60 4 61 3 62 6 63 10 64 10 65 5 66 4 67 4 69 1 70 1 51 59 2 60 3 61 3 62 5 63 9 64 10 65 5 66 4 67 4 69 1 70 1 47 w maxs cone=. 707 0 2 F=(y-M)o(x-M)/|x-M|-mn 8 1 restricted to a cosine cone 10 3 12 2 13 1 on IRIS 14 3 15 1 16 3 17 5 18 3 19 5 x=i 1 20 6 cone=. 707 21 2 22 4 x=e 1 34 1 23 3 cone=. 707 35 1 24 3 36 2 25 9 33 1 37 2 26 3 36 2 38 3 27 3 37 2 39 5 28 3 38 3 40 4 29 5 39 1 42 6 30 3 40 5 43 2 31 4 44 7 32 3 42 2 45 5 33 2 43 1 47 2 34 2 44 1 48 3 35 2 45 6 49 3 36 4 46 4 50 3 37 1 47 5 51 4 38 1 48 1 52 3 40 1 49 2 53 2 41 4 50 5 54 2 42 5 51 1 55 4 43 5 52 2 56 2 44 7 54 2 57 1 45 3 55 1 58 1 46 1 57 2 59 1 47 6 58 1 60 1 48 6 60 1 61 1 49 2 62 1 51 1 63 1 52 2 64 1 53 1 65 2 66 1 55 1 60 75 137 x=s 2 cone=. 1 w maxs-to-mins cone=. 939 w naaa-xaaa cone=. 95 39 2 40 1 41 1 44 1 45 1 46 1 47 1 52 1 i 39 59 2 60 4 61 3 62 6 63 10 64 10 65 5 66 4 67 4 69 1 70 1 59 14 1 i 25 16 1 i 40 18 2 i 16 i 42 19 2 i 17 i 38 20 2 i 11 i 48 22 2 23 1 24 4 i 34 i 50 25 3 i 24 i 28 26 3 i 27 27 5 28 3 29 2 30 2 31 3 32 4 34 3 35 4 36 2 37 2 38 2 39 3 40 1 41 2 46 1 47 2 48 1 49 1 i 39 53 1 54 2 55 1 56 1 57 8 58 5 59 4 60 7 61 4 62 5 63 5 64 1 65 3 66 1 67 1 68 1 114 14 i and 100 s/e. So picks i as 0 w xnnn-nxxx cone=. 95 12 1 13 2 14 1 15 2 16 1 17 1 18 4 19 3 20 2 21 3 22 5 23 6 i 21 24 5 25 1 27 1 28 1 29 2 30 2 i 7 41/43 e so picks e w maxs cone=. 93 8 1 i 10 13 1 14 3 16 2 17 2 18 1 19 3 20 4 21 1 24 1 25 4 26 1 e 21 e 34 27 2 29 2 37 1 i 7 27/29 are i's w maxs cone=. 925 8 1 i 10 13 1 14 3 16 3 17 2 18 2 19 3 20 4 21 1 24 1 25 5 26 1 e 21 e 34 27 2 28 1 29 2 31 1 e 35 37 1 i 7 31/34 are i's Gap in dot product projections onto the cornerpoints line. Cosine cone gap (over some angle) Corner points w aaan-aaax cone=. 54 7 3 i 27 i 28 8 1 9 3 10 12 i 20 i 34 11 7 12 13 13 5 14 3 15 7 19 1 20 1 21 7 22 7 23 28 24 6 100/104 s or e so 0 picks i 8 2 i 22 i 50 10 2 11 2 i 28 12 4 i 27 i 34 13 2 14 4 15 3 16 8 17 4 18 7 19 3 20 5 21 1 22 1 23 1 34 1 i 39 43/50 e so picks out e Cosine conical gapping seems quick and easy (cosine = dot product divided by both lengths. Length of the fixed vector, x-M, is a one-time calculation. Length y-M changes with y so build the PTree. Set.
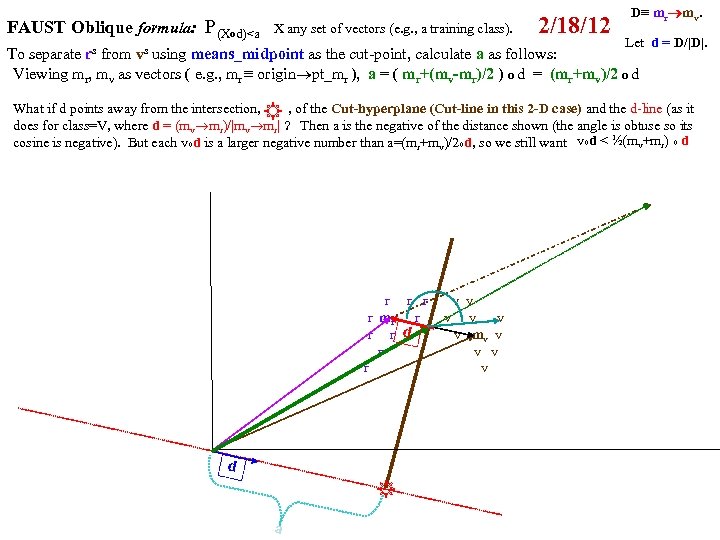
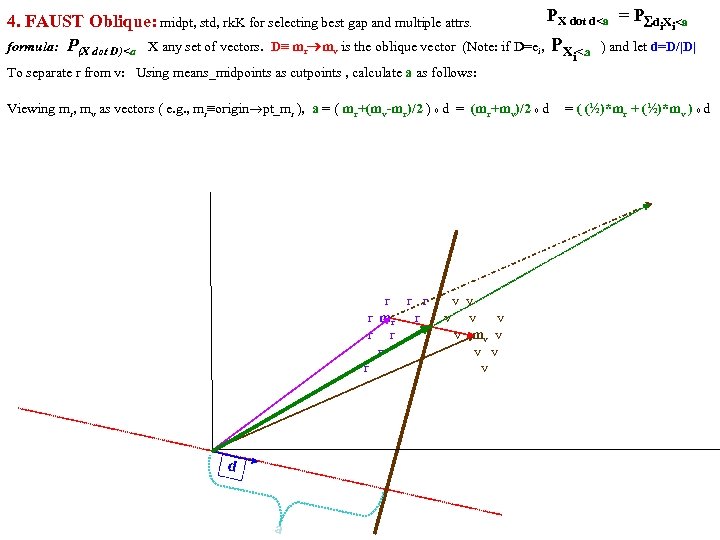
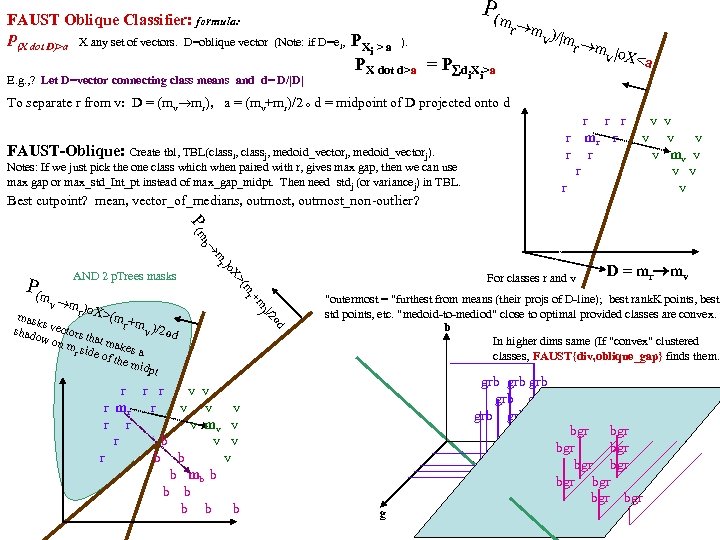FAUST Oblique Classifier: formula: P(X dot D)>a X any set of vectors. D=oblique vector (Note: if D=ei, PX E. g. , ? Let D=vector connecting class means and d= D/|D| P(m i > a ). PX dot d>a = P d X >a i i r m )/ v |m r m |o v X< a To separate r from v: D = (mv mr), a = (mv+mr)/2 o d = midpoint of D projected onto d FAUST-Oblique: Create tbl, TBL(classi, classj, medoid_vectori, medoid_vectorj). Notes: If we just pick the one class which when paired with r, gives max gap, then we can use max gap or max_std_Int_pt instead of max_gap_midpt. Then need stdj (or variancej) in TBL. Best cutpoint? mean, vector_of_medians, outmost_non-outlier? r r r v v r mr r v v v r r v mv v r v v r v P (m b a For classes r and v +m (m r X> od w on rs that m akes m si r de of th a e mid pt r r r v v r mr r v v v r r v mv v r b v v r b b v b mb b b b b b b od hado |/2 ) v m )o r X>(m mask s vec r +mv )/2 to s )o mr P(m AND 2 p. Trees masks D = mr mv "outermost = "furthest from means (their projs of D-line); best rank. K points, best std points, etc. "medoid-to-mediod" close to optimal provided classes are convex. b In higher dims same (If "convex" clustered classes, FAUST{div, oblique_gap} finds them. grb grb bgr D bgr grb bgr g r
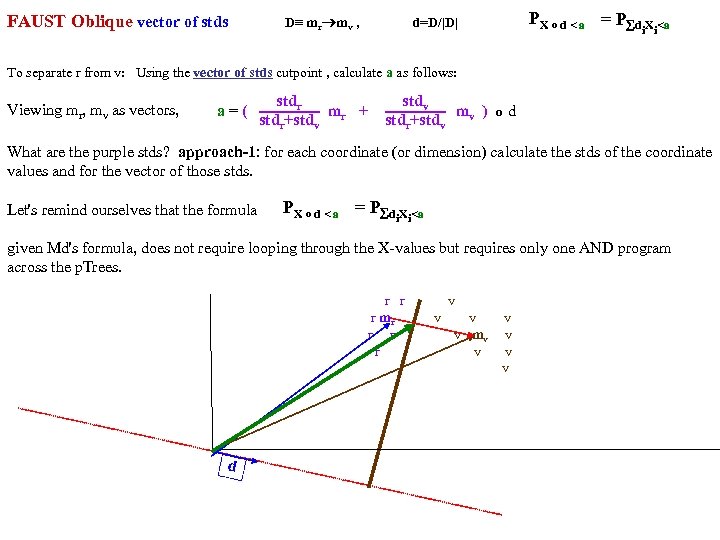
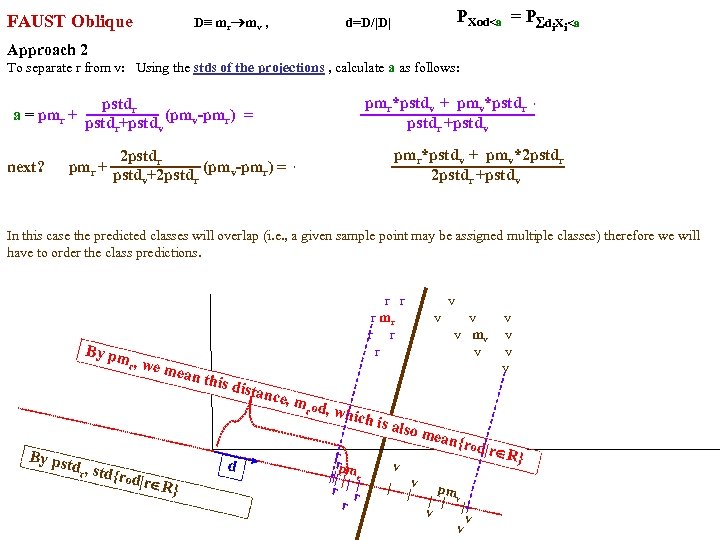
Separate class. R, class. V using midpoints of means (mom) method: calc a midpoints of means (mom) FAUST Oblique PR = P(X dot d)
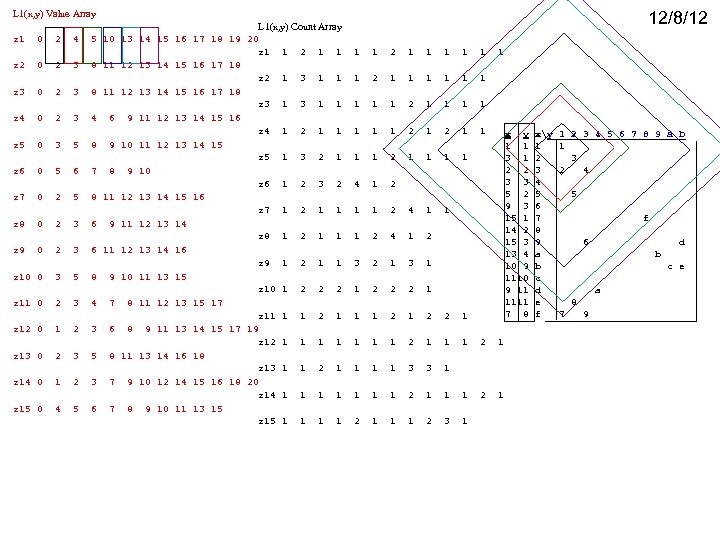L 1(x, y) Value Array 12/8/12 L 1(x, y) Count Array z 1 0 2 4 5 10 13 14 15 16 17 18 19 20 z 1 1 2 1 1 1 1 z 2 0 2 3 8 11 12 13 14 15 16 17 18 z 2 1 3 1 1 1 2 1 1 1 z 3 0 2 3 8 11 12 13 14 15 16 17 18 z 3 1 1 1 2 1 1 z 4 0 2 3 4 6 9 11 12 13 14 15 16 z 4 1 2 1 1 x y xy 1 2 3 4 5 6 7 8 9 a b z 5 0 3 5 8 9 10 11 12 13 14 15 1 1 1 1 z 5 1 3 2 1 1 1 1 3 1 2 3 2 2 3 2 4 z 6 0 5 6 7 8 9 10 3 3 4 z 6 1 2 3 2 4 1 2 5 5 z 7 0 2 5 8 11 12 13 14 15 16 9 3 6 z 7 1 2 1 1 2 4 1 1 15 1 7 f z 8 0 2 3 6 9 11 12 13 14 14 2 8 z 8 1 2 1 1 1 2 4 1 2 15 3 9 6 d z 9 0 2 3 6 11 12 13 14 16 13 4 a b z 9 1 2 1 1 3 2 1 3 1 10 9 b c e z 10 0 3 5 8 9 10 11 13 15 1110 c z 10 1 2 2 2 1 9 11 d a 1111 e 8 z 11 0 2 3 4 7 8 11 12 13 15 17 7 8 f 7 9 z 11 1 1 2 1 2 2 1 z 12 0 1 2 3 6 8 9 11 13 14 15 17 19 z 12 1 1 1 1 2 1 z 13 0 2 3 5 8 11 13 14 16 18 z 13 1 1 2 1 1 3 3 1 z 14 0 1 2 3 7 9 10 12 14 15 16 18 20 z 14 1 1 1 1 2 1 z 15 0 4 5 6 7 8 9 10 11 13 15 z 15 1 1 2 1 1 1 2 3 1
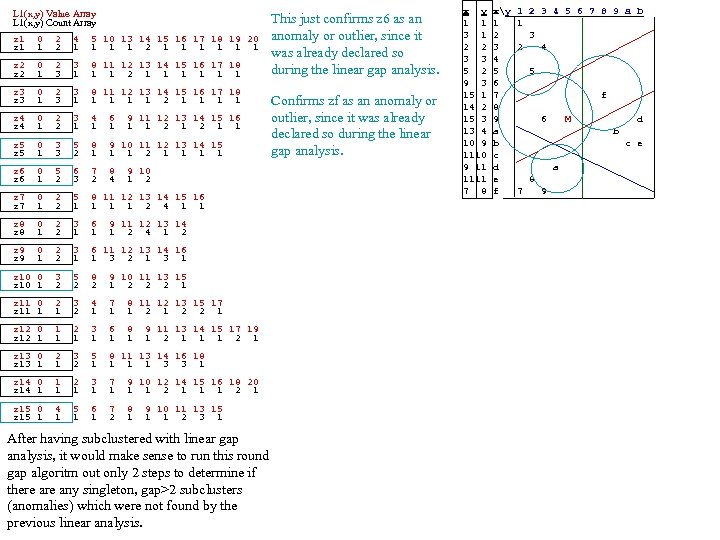L 1(x, y) Value Array L 1(x, y) Count Array z 1 0 2 4 5 10 13 14 15 16 17 18 19 20 z 1 1 2 1 1 1 1 z 2 0 2 3 8 11 12 13 14 15 16 17 18 z 2 1 3 1 1 1 2 1 1 1 z 3 0 2 3 8 11 12 13 14 15 16 17 18 z 3 1 1 1 2 1 1 z 4 0 2 3 4 6 9 11 12 13 14 15 16 z 4 1 2 1 1 z 5 0 3 5 8 9 10 11 12 13 14 15 z 5 1 3 2 1 1 1 1 This just confirms z 6 as an anomaly or outlier, since it was already declared so during the linear gap analysis. Confirms zf as an anomaly or outlier, since it was already declared so during the linear gap analysis. z 6 0 5 6 7 8 9 10 z 6 1 2 3 2 4 1 2 z 7 0 2 5 8 11 12 13 14 15 16 z 7 1 2 1 1 2 4 1 1 z 8 0 2 3 6 9 11 12 13 14 z 8 1 2 1 1 1 2 4 1 2 z 9 0 2 3 6 11 12 13 14 16 z 9 1 2 1 1 3 2 1 3 1 z 10 0 3 5 8 9 10 11 13 15 z 10 1 2 2 2 1 z 11 0 2 3 4 7 8 11 12 13 15 17 z 11 1 1 2 1 2 2 1 z 12 0 1 2 3 6 8 9 11 13 14 15 17 19 z 12 1 1 1 1 2 1 z 13 0 2 3 5 8 11 13 14 16 18 z 13 1 1 2 1 1 3 3 1 z 14 0 1 2 3 7 9 10 12 14 15 16 18 20 z 14 1 1 1 1 2 1 z 15 0 4 5 6 7 8 9 10 11 13 15 z 15 1 1 2 1 1 1 2 3 1 After having subclustered with linear gap analysis, it would make sense to run this round gap algoritm out only 2 steps to determine if there any singleton, gap>2 subclusters (anomalies) which were not found by the previous linear analysis. x y xy 1 2 3 4 5 6 7 8 9 a b 1 1 1 1 3 1 2 3 2 2 3 2 4 3 3 4 5 2 5 5 9 3 6 15 1 7 f 14 2 8 15 3 9 6 M d 13 4 a b 10 9 b c e 1110 c 9 11 d a 1111 e 8 7 8 f 7 9
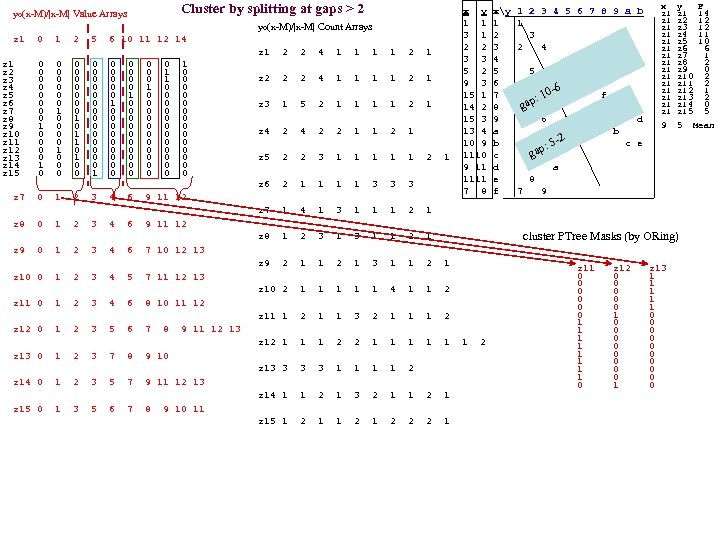yo(x-M)/|x-M| Value Arrays Cluster by splitting at gaps > 2 yo(x-M)/|x-M| Count Arrays z 1 0 1 2 5 6 10 11 12 14 z 1 2 2 4 1 1 2 1 0 0 0 0 1 z 1 z 2 0 1 2 5 6 10 11 12 14 0 0 0 0 1 0 z 2 0 0 0 0 1 0 z 3 0 0 0 1 0 0 z 4 z 3 0 1 2 5 6 10 11 12 14 0 0 0 1 0 0 0 z 5 0 0 1 0 0 z 6 0 1 0 0 0 0 z 7 0 0 1 0 0 0 z 8 z 4 0 1 3 6 10 11 12 14 1 0 0 0 0 z 9 z 10 0 0 1 0 0 0 z 11 0 0 0 0 z 5 0 1 2 3 5 6 10 11 12 14 z 12 0 1 0 0 0 0 z 13 0 0 1 0 0 0 z 14 1 0 0 0 0 z 6 0 1 2 3 7 8 9 10 z 15 0 0 0 1 0 0 0 z 2 2 2 4 1 1 2 1 z 3 1 5 2 1 1 2 1 z 4 2 2 1 1 2 1 z 5 2 2 3 1 1 1 2 1 z 6 2 1 1 3 3 3 z 7 0 1 2 3 4 6 9 11 12 x y xy 1 2 3 4 5 6 7 8 9 a b 1 1 1 1 3 1 2 3 2 2 3 2 4 3 3 4 5 2 5 5 9 3 6 -6 15 1 7 f : 10 gap 14 2 8 15 3 9 6 M d 13 4 a b 10 9 b c e 5 -2 ap: g 1110 c 9 11 d a 1111 e 8 7 8 f 7 9 x y F z 1 14 z 1 z 2 12 z 1 z 3 12 z 1 z 4 11 z 5 10 z 1 z 6 6 z 1 z 7 1 z 8 2 z 1 z 9 0 z 10 2 z 11 2 z 12 1 z 13 2 z 14 0 z 15 5 9 5 Mean z 7 1 4 1 3 1 1 1 2 1 z 8 0 1 2 3 4 6 9 11 12 z 8 1 2 3 1 1 2 1 cluster PTree Masks (by ORing) z 9 0 1 2 3 4 6 7 10 12 13 z 9 2 1 1 2 1 3 1 1 2 1 z 10 0 1 2 3 4 5 7 11 12 13 z 10 2 1 1 1 4 1 1 2 z 11 0 1 2 3 4 6 8 10 11 12 z 11 1 2 1 1 3 2 1 1 1 2 z 12 0 1 2 3 5 6 7 8 9 11 12 13 z 12 1 1 1 2 z 13 0 1 2 3 7 8 9 10 z 13 3 1 1 2 z 14 0 1 2 3 5 7 9 11 12 13 z 14 1 1 2 1 3 2 1 1 2 1 z 15 0 1 3 5 6 7 8 9 10 11 z 15 1 2 1 2 2 2 1 z 11 0 0 0 1 1 1 1 0 z 12 0 0 0 1 0 0 0 0 1 z 13 1 1 1 0 0 0 0 0
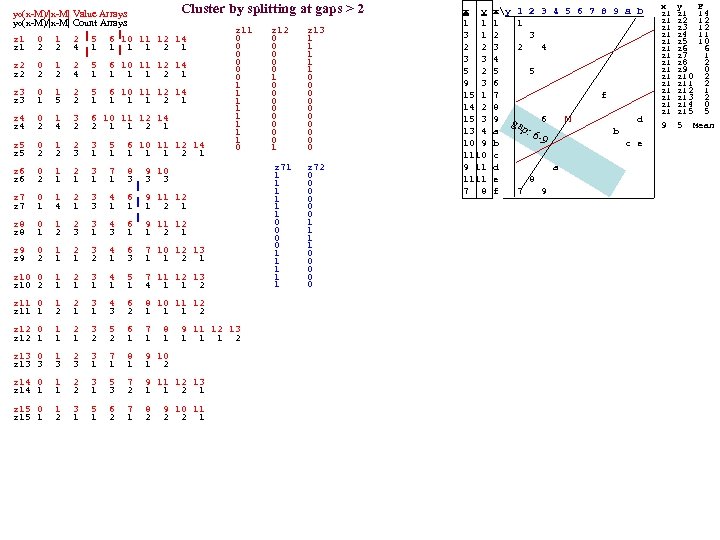yo(x-M)/|x-M| Value Arrays yo(x-M)/|x-M| Count Arrays Cluster by splitting at gaps > 2 z 1 0 1 2 5 6 10 11 12 14 z 1 2 2 4 1 1 2 1 z 2 0 1 2 5 6 10 11 12 14 z 2 2 2 4 1 1 2 1 z 3 0 1 2 5 6 10 11 12 14 z 3 1 5 2 1 1 2 1 z 4 0 1 3 6 10 11 12 14 z 4 2 2 1 1 2 1 z 5 0 1 2 3 5 6 10 11 12 14 z 5 2 2 3 1 1 1 2 1 z 11 0 0 0 1 1 1 1 0 z 6 0 1 2 3 7 8 9 10 z 6 2 1 1 3 3 3 z 7 0 1 2 3 4 6 9 11 12 z 7 1 4 1 3 1 1 1 2 1 z 8 0 1 2 3 4 6 9 11 12 z 8 1 2 3 1 1 2 1 z 9 0 1 2 3 4 6 7 10 12 13 z 9 2 1 1 2 1 3 1 1 2 1 z 10 0 1 2 3 4 5 7 11 12 13 z 10 2 1 1 1 4 1 1 2 z 11 0 1 2 3 4 6 8 10 11 12 z 11 1 2 1 1 3 2 1 1 1 2 z 12 0 1 2 3 5 6 7 8 9 11 12 13 z 12 1 1 1 2 z 13 0 1 2 3 7 8 9 10 z 13 3 1 1 2 z 14 0 1 2 3 5 7 9 11 12 13 z 14 1 1 2 1 3 2 1 1 2 1 z 15 0 1 3 5 6 7 8 9 10 11 z 15 1 2 1 2 2 2 1 z 12 0 0 0 1 0 0 0 0 1 z 13 1 1 1 0 0 0 0 0 z 71 1 1 1 0 0 1 1 1 z 72 0 0 0 1 1 0 0 0 x y xy 1 2 3 4 5 6 7 8 9 a b 1 1 1 1 3 1 2 3 2 2 3 2 4 3 3 4 5 2 5 5 9 3 6 15 1 7 f 14 2 8 15 3 9 6 M d gap : 6 13 4 a b -9 10 9 b c e 1110 c 9 11 d a 1111 e 8 7 8 f 7 9 x y F z 1 14 z 1 z 2 12 z 1 z 3 12 z 1 z 4 11 z 5 10 z 1 z 6 6 z 1 z 7 1 z 8 2 z 1 z 9 0 z 10 2 z 11 2 z 12 1 z 13 2 z 14 0 z 15 5 9 5 Mean
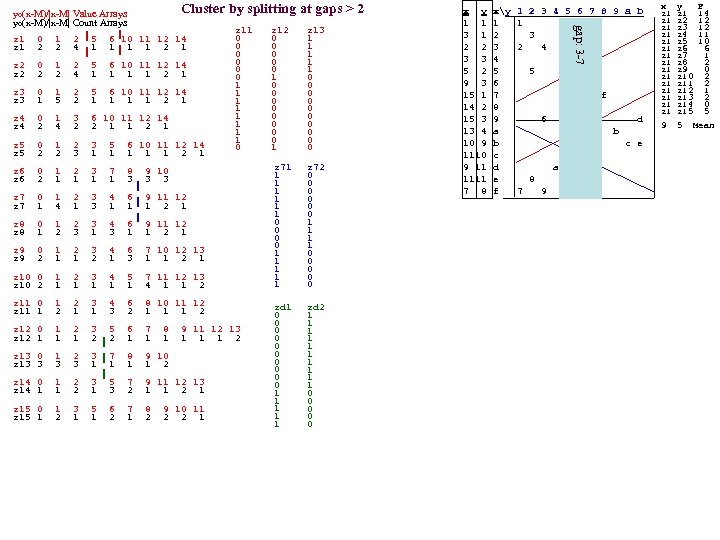Cluster by splitting at gaps > 2 z 1 0 1 2 5 6 10 11 12 14 z 1 2 2 4 1 1 2 1 z 2 0 1 2 5 6 10 11 12 14 z 2 2 2 4 1 1 2 1 z 3 0 1 2 5 6 10 11 12 14 z 3 1 5 2 1 1 2 1 z 4 0 1 3 6 10 11 12 14 z 4 2 2 1 1 2 1 z 5 0 1 2 3 5 6 10 11 12 14 z 5 2 2 3 1 1 1 2 1 z 11 0 0 0 1 1 1 1 0 z 6 0 1 2 3 7 8 9 10 z 6 2 1 1 3 3 3 z 7 0 1 2 3 4 6 9 11 12 z 7 1 4 1 3 1 1 1 2 1 z 8 0 1 2 3 4 6 9 11 12 z 8 1 2 3 1 1 2 1 z 9 0 1 2 3 4 6 7 10 12 13 z 9 2 1 1 2 1 3 1 1 2 1 z 10 0 1 2 3 4 5 7 11 12 13 z 10 2 1 1 1 4 1 1 2 z 11 0 1 2 3 4 6 8 10 11 12 z 11 1 2 1 1 3 2 1 1 1 2 z 12 0 1 2 3 5 6 7 8 9 11 12 13 z 12 1 1 1 2 z 13 0 1 2 3 7 8 9 10 z 13 3 1 1 2 z 14 0 1 2 3 5 7 9 11 12 13 z 14 1 1 2 1 3 2 1 1 2 1 z 15 0 1 3 5 6 7 8 9 10 11 z 15 1 2 1 2 2 2 1 z 12 0 0 0 1 0 0 0 0 1 z 13 1 1 1 0 0 0 0 0 z 71 1 1 1 0 0 1 1 1 z 72 0 0 0 1 1 0 0 0 zd 1 0 0 0 0 0 1 1 1 zd 2 1 1 1 1 1 0 0 0 x y xy 1 2 3 4 5 6 7 8 9 a b 1 1 1 1 3 1 2 3 2 2 3 2 4 3 3 4 5 2 5 5 9 3 6 15 1 7 f 14 2 8 15 3 9 6 M d 13 4 a b 10 9 b c e 1110 c 9 11 d a 1111 e 8 7 8 f 7 9 gap: 3 -7 yo(x-M)/|x-M| Value Arrays yo(x-M)/|x-M| Count Arrays x y F z 1 14 z 1 z 2 12 z 1 z 3 12 z 1 z 4 11 z 5 10 z 1 z 6 6 z 1 z 7 1 z 8 2 z 1 z 9 0 z 10 2 z 11 2 z 12 1 z 13 2 z 14 0 z 15 5 9 5 Mean
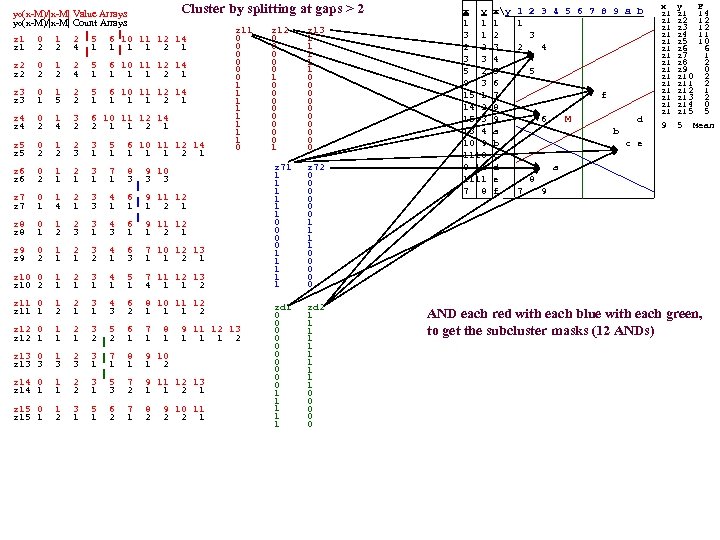yo(x-M)/|x-M| Value Arrays yo(x-M)/|x-M| Count Arrays Cluster by splitting at gaps > 2 z 1 0 1 2 5 6 10 11 12 14 z 1 2 2 4 1 1 2 1 z 2 0 1 2 5 6 10 11 12 14 z 2 2 2 4 1 1 2 1 z 3 0 1 2 5 6 10 11 12 14 z 3 1 5 2 1 1 2 1 z 4 0 1 3 6 10 11 12 14 z 4 2 2 1 1 2 1 z 5 0 1 2 3 5 6 10 11 12 14 z 5 2 2 3 1 1 1 2 1 z 11 0 0 0 1 1 1 1 0 z 6 0 1 2 3 7 8 9 10 z 6 2 1 1 3 3 3 z 7 0 1 2 3 4 6 9 11 12 z 7 1 4 1 3 1 1 1 2 1 z 8 0 1 2 3 4 6 9 11 12 z 8 1 2 3 1 1 2 1 z 9 0 1 2 3 4 6 7 10 12 13 z 9 2 1 1 2 1 3 1 1 2 1 z 10 0 1 2 3 4 5 7 11 12 13 z 10 2 1 1 1 4 1 1 2 z 11 0 1 2 3 4 6 8 10 11 12 z 11 1 2 1 1 3 2 1 1 1 2 z 12 0 1 2 3 5 6 7 8 9 11 12 13 z 12 1 1 1 2 z 13 0 1 2 3 7 8 9 10 z 13 3 1 1 2 z 14 0 1 2 3 5 7 9 11 12 13 z 14 1 1 2 1 3 2 1 1 2 1 z 15 0 1 3 5 6 7 8 9 10 11 z 15 1 2 1 2 2 2 1 z 12 0 0 0 1 0 0 0 0 1 z 13 1 1 1 0 0 0 0 0 z 71 1 1 1 0 0 1 1 1 z 72 0 0 0 1 1 0 0 0 zd 1 0 0 0 0 0 1 1 1 zd 2 1 1 1 1 1 0 0 0 x y xy 1 2 3 4 5 6 7 8 9 a b 1 1 1 1 3 1 2 3 2 2 3 2 4 3 3 4 5 2 5 5 9 3 6 15 1 7 f 14 2 8 15 3 9 6 M d 13 4 a b 10 9 b c e 1110 c 9 11 d a 1111 e 8 7 8 f 7 9 x y F z 1 14 z 1 z 2 12 z 1 z 3 12 z 1 z 4 11 z 5 10 z 1 z 6 6 z 1 z 7 1 z 8 2 z 1 z 9 0 z 10 2 z 11 2 z 12 1 z 13 2 z 14 0 z 15 5 9 5 Mean AND each red with each blue with each green, to get the subcluster masks (12 ANDs)
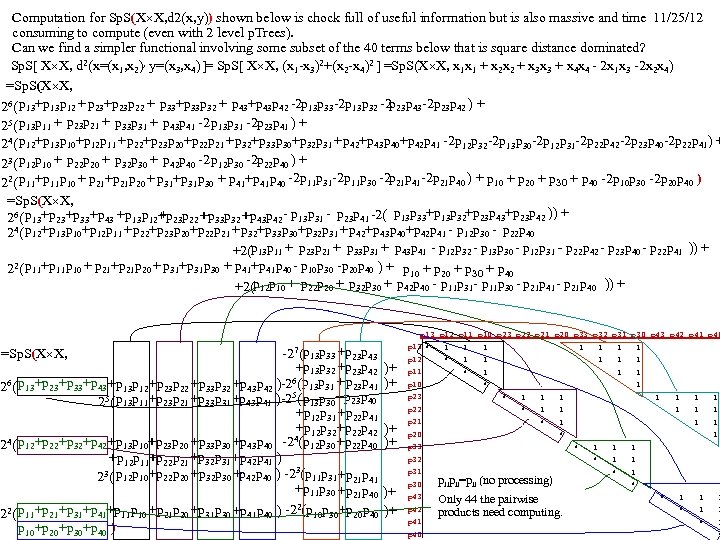Computation for Sp. S(X X, d 2(x, y)) shown below is chock full of useful information but is also massive and time 11/25/12 consuming to compute (even with 2 level p. Trees). Can we find a simpler functional involving some subset of the 40 terms below that is square distance dominated? Sp. S[ X X, d 2(x=(x 1, x 2), y=(x 3, x 4) ]= Sp. S[ X X, (x 1 -x 3)2+(x 2 -x 4)2 ] =Sp. S(X X, x 1 x 1 + x 2 x 2 + x 3 x 3 + x 4 x 4 - 2 x 1 x 3 -2 x 2 x 4) =Sp. S(X X, 26( p 13+p 13 p 12 + p 23+p 23 p 22 + p 33+p 33 p 32 + p 43+p 43 p 42 -2 p 13 p 33 -2 p 13 p 32 -2 p 23 p 43 -2 p 23 p 42 ) + 25( p 13 p 11 + p 23 p 21 + p 33 p 31 + p 43 p 41 -2 p 13 p 31 -2 p 23 p 41 ) + 24( p 12+p 13 p 10+p 12 p 11 + p 22+p 23 p 20+p 22 p 21 +p 32+p 33 p 30+p 32 p 31 +p 42+p 43 p 40+p 42 p 41 -2 p 12 p 32 -2 p 13 p 30 -2 p 12 p 31 -2 p 22 p 42 -2 p 23 p 40 -2 p 22 p 41) + 23( p 12 p 10 + p 22 p 20 + p 32 p 30 + p 42 p 40 -2 p 12 p 30 -2 p 22 p 40 ) + 22( p 11+p 11 p 10 + p 21+p 21 p 20 + p 31+p 31 p 30 + p 41+p 41 p 40 -2 p 11 p 31 -2 p 11 p 30 -2 p 21 p 41 -2 p 21 p 40 ) + p 10 + p 20 + p 30 + p 40 -2 p 10 p 30 -2 p 20 p 40 ) =Sp. S(X X, + 26( p 13+p 23+p 33+p 43 +p 13 p 12 +p 23 p 22 +p 33 p 32 +p 43 p 42 - p 13 p 31 - p 23 p 41 -2( p 13 p 33+p 13 p 32+p 23 p 43+p 23 p 42 )) + 24( p 12+p 13 p 10+p 12 p 11 +p 22+p 23 p 20+p 22 p 21 +p 32+p 33 p 30+p 32 p 31 +p 42+p 43 p 40+p 42 p 41 - p 12 p 30 - p 22 p 40 +2(p 13 p 11 + p 23 p 21 + p 33 p 31 + p 43 p 41 - p 12 p 32 - p 13 p 30 - p 12 p 31 - p 22 p 42 - p 23 p 40 - p 22 p 41 )) + 22( p 11+p 11 p 10 + p 21+p 21 p 20 + p 31+p 31 p 30 + p 41+p 41 p 40 - p 10 p 30 -p 20 p 40 ) + p 10 + p 20 + p 30 + p 40 +2(p 12 p 10 + p 22 p 20 + p 32 p 30 + p 42 p 40 - p 11 p 31 - p 11 p 30 - p 21 p 41 - p 21 p 40 )) + -27(p 13 p 33 +p 23 p 43 +p 13 p 32 +p 23 p 42 6( 26( p 13+p 23+p 33+p 43 +p 13 p 12+p 23 p 22 +p 33 p 32 +p 43 p 42 )-2 p 13 p 31 + p 23 p 41 5 25( p 13 p 11+p 23 p 21 +p 33 p 31 +p 43 p 41 )-2 (p 13 p 30 +p 23 p 40 +p 12 p 31 +p 22 p 41 +p 12 p 32 +p 22 p 42 4( p 12+p 22+p 32+p 42 +p 13 p 10+p 23 p 20 +p 33 p 30 +p 43 p 40 -24(p 12 p 30 +p 22 p 40 + 2 +p 12 p 11+p 22 p 21 +p 32 p 31 +p 42 p 41 ) 3 23( p 12 p 10+p 22 p 20 +p 32 p 30 +p 42 p 40 ) -2 (p 11 p 31 +p 21 p 41 +p 11 p 30 +p 21 p 40 2 + 22( p 11+p 21+p 31+p 41+p 11 p 10 +p 21 p 20 +p 31 p 30 +p 41 p 40 ) -2 (p 10 p 30+p 20 p 40 p 10+p 20+p 30+p 40 ) =Sp. S(X X, )+ )+ p 13 p 12 p 11 p 10 p 23 p 22 p 21 p 20 p 33 p 32 p 31 p 30 p 43 p 42 p 41 p 40 p 13 * 1 1 p 12 * 1 1 1 p 11 * 1 1 1 p 10 * 1 p 23 * 1 1 p 22 * 1 1 1 )+ )+ p 21 * 1 1 1 p 20 * 1 p 33 * 1 1 1 p 32 * 1 1 p 31 * 1 p 30 piipii=pii (no processing) * p 43 Only 44 the pairwise * 1 1 1 p 42 products need computing. * 1 1 p 41 * 1 p 40 *
The computation for Sp. S(X X, d 2(x, y)) is massive and time consuming (even with 2 level p. Trees). Can we use a simpler distance dominated functional? Here we try a Manhattan_distance based functional: L 1(x, y)≡ i=1. . n|xi-yi| Claim L 1(x, y) L 2(x, y)≡( i=1. . n(xi-yi)2)½ / √ 2 Proof: on x 2+y 2=1, f(x, y) = x+y , so f(x)= x + (1 -x 2)½ f'(x) = 1 + ½(1 -x 2)-½ (-2 x) = 0 1 = x / (1 -x 2)-½ 1 -x 2 = x 2 1= 2 x 2 1/2= x 2 1 = x 2 / 1 -x 2 1/√ 2= x p. Tree Operations: +, -, *, . . . input_operands=p. Trees output=p. Tree PTree. Set Operations (column ops): +, -, *, max, min, rank. K, . . . input_operands=PTree. Sets output=PTree. Set Table Functionals (p. Trees and PTree. Sets are tables too!): col_max, col_min, col_rank. K, max of lin combo of cols, . . . input_operand=table output=column of reals or a PTree. Set Table Functional Contour: Max. Pts, Min. Pts, Ran. KPts, . . . input_operand=table, functional, set of reals. output=mask p. Tree of the set of points that map into that set of reals under that functional on that table.
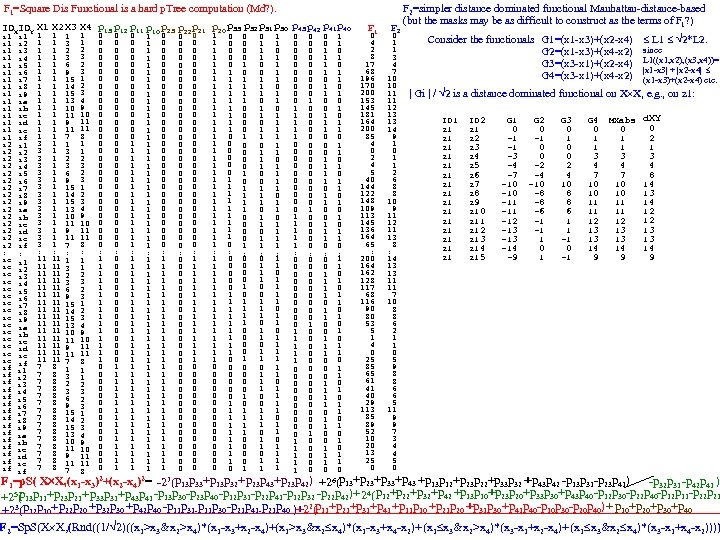F 1=Square Dis Functional is a hard p. Tree computation (Md? ). IDXIDY X 1 X 2 X 3 X 4 p 13 p 12 p 11 p 10 p 23 p 22 p 21 p 20 p 33 p 32 p 31 p 30 p 43 p 42 p 41 p 40 z 1 z 1 z 1 z 1 z 2 z 2 z 2 z 2 : ze ze ze ze zf zf zf zf z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 za zb zc zd ze zf : z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 za zb zc zd ze zf 1 1 1 1 3 3 3 3 : 11 11 11 11 7 7 7 7 1 1 1 1 1 1 1 1 : 11 11 11 11 8 8 8 8 1 3 2 3 6 9 15 14 15 13 10 11 9 11 7 : 1 3 2 3 6 9 15 14 15 13 10 11 9 11 7 1 1 2 3 2 3 1 2 3 4 9 10 11 11 8 : 1 1 2 3 2 3 1 2 3 4 9 10 11 11 8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 : : 1 0 1 0 1 0 1 0 0 1 0 1 0 1 0 1 )2+(x 0 0 0 0 1 1 1 1 1 1 1 1 : 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 : 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 : 1 1 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 1 1 1 1 1 0 : 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 0 1 1 1 1 0 0 0 0 1 : 0 0 0 0 1 0 1 1 1 1 0 0 0 0 1 0 1 1 1 0 1 1 0 1 1 : 0 1 1 1 0 1 1 0 1 1 1 1 0 1 1 1 1 : 1 1 0 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 : 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 0 0 0 0 0 : 0 0 0 0 0 1 0 0 0 0 1 1 1 1 0 0 1 1 1 0 : 0 0 1 1 1 1 0 0 1 1 1 0 1 0 1 0 1 0 1 1 0 : 1 1 0 1 0 1 0 1 1 0 F 1 0 4 2 8 17 68 196 170 200 153 145 181 164 200 85 4 0 2 4 5 40 144 122 148 109 113 145 136 164 65 : 200 164 162 128 117 68 116 90 80 53 5 1 4 0 25 85 65 61 41 40 29 113 85 89 52 10 20 13 25 0 F 2 0 1 1 3 4 7 10 10 11 11 12 13 13 14 9 1 0 1 1 2 6 8 8 10 9 11 12 11 13 8 : 14 13 13 11 11 7 10 8 8 6 2 1 1 0 5 9 8 8 6 6 5 11 9 9 7 3 4 4 5 0 F 2=simpler distance dominated functional Manhattan-distance-based (but the masks may be as difficult to construct as the terms of F 1? ) Consider the functionals G 1=(x 1 -x 3)+(x 2 -x 4) G 2=(x 1 -x 3)+(x 4 -x 2) G 3=(x 3 -x 1)+(x 2 -x 4) G 4=(x 3 -x 1)+(x 4 -x 2) L 1 √ 2*L 2. since L 1((x 1, x 2), (x 3, x 4))= |x 1 -x 3| + |x 2 -x 4| (x 1 -x 3)+(x 2 -x 4) etc. | Gi | / √ 2 is a distance dominated functional on X X, e. g. , on z 1: ID 1 ID 2 G 1 G 2 G 3 G 4 MXabs z 1 0 0 0 z 1 z 2 -1 1 z 1 z 3 -1 0 0 1 1 z 1 z 4 -3 0 0 3 3 z 1 z 5 -4 -2 2 4 4 z 1 z 6 -7 -4 4 7 7 z 1 z 7 -10 10 10 z 1 z 8 -10 -8 8 10 z 1 z 9 -11 -8 8 11 z 10 -11 -6 6 11 z 11 -12 -1 1 12 z 12 -13 -1 1 13 z 13 -13 1 -1 13 z 14 -14 0 0 14 z 15 -9 1 -1 9 9 d. XY 0 2 1 3 4 8 14 13 14 12 12 13 13 14 9 2 7 p F 1=p. S( X X, (x 1 -x 3 -p 32 p 31 -p 42 p 41 ) +26 p +p 23+p 33+p 43 +p 13 p 12+p 23 p 22+p 33 p 32 + p 43 p 42 -p 13 p 31 - 23 p 41) 2 -x 4) = -2 (p 13 p 33+p 13 p 32+ p 23 p 43+p 23 p 42) ( 13 4( p 12+p 22+p 32+p 42 +p 13 p 10+ 23 p 20 +p +p 43 p 40 -p 12 p 30 -p 22 p 40 -p 12 p 11 -p 22 p 21 +p 33 p 30 5( 13 p 11+p 23 p 21+ p 33 p 31+ p 43 p 41 -p 13 p 30 -p 23 p 40 -p 12 p 31 -p 22 p 41 -p 12 p 32 -p 22 p 42)+ 2 p +2 +p + +23(p 12 p 10+ p 22 p 20 +p 32 p 30 +p 42 p 40 -p 11 p 31 -p 11 p 30 -p 21 p 41 -p 21 p 40 )+22(p 11+p 21+p 31+p 41 +p 11 p 10 + 21 p 20 + p 31 p 30 +p 41 p 40 -p 10 p 30 -p 20 p 40) + p 10+p 20+p 30+p 40 F 2=Sp. S(X X, (Rnd((1/√ 2)((x 1>x 3&x 2>x 4)*(x 1 -x 3+x 2 -x 4)+ x 1>x 3&x 2 x 4)*(x 1 -x 3+x 4 -x 2)+ (x 1 x 3&x 2>x 4)*(x 3 -x 1+x 2 -x 4)+ (x 1 x 3&x 2 x 4)*(x 3 -x 1+x 4 -x 2)))) (
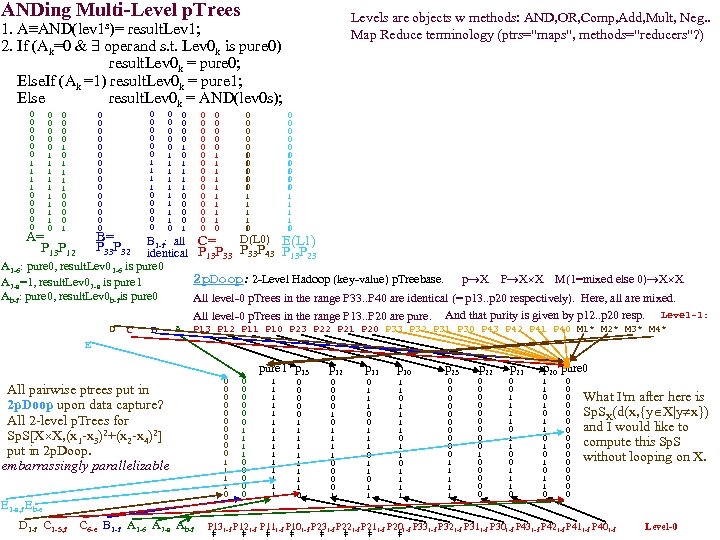ANDing Multi-Level p. Trees Levels are objects w methods: AND, OR, Comp, Add, Mult, Neg. . Map Reduce terminology (ptrs="maps", methods="reducers"? ) 1. A≡AND(lev 1 s)= result. Lev 1; 2. If (Ak=0 & operand s. t. Lev 0 k is pure 0) result. Lev 0 k = pure 0; Else. If (Ak =1) result. Lev 0 k = pure 1; Else result. Lev 0 k = AND(lev 0 s); 0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 1 0 1 1 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 1 0 1 0 1 1 1 0 0 0 1 0 1 1 0 1 B= D(L 0) P 33 P 32 B 1 -f: all C=P P 33 P 43 E(L 1) P 13 33 P 13 P 23 identical A= E. g. , P 13 P 12 A 1 -6: pure 0, result. Lev 01 -6 is pure 0 A 7 -a=1, result. Lev 07 -a is pure 1 Ab-f: pure 0, result. Lev 0 b-fis pure 0 D C B 2 p. Doop: 2 -Level Hadoop (key-value) p. Treebase. p X P X X M(1=mixed else 0) X X All level-0 p. Trees in the range P 33. . P 40 are identical (= p 13. . p 20 respectively). Here, all are mixed. Level-1: All level-0 p. Trees in the range P 13. . P 20 are pure. And that purity is given by p 12. . p 20 resp. A P 13 P 12 P 11 P 10 P 23 P 22 P 21 P 20 P 33 P 32 P 31 P 30 P 43 P 42 P 41 P 40 M 1* M 2* M 3* M 4* E All pairwise ptrees put in 2 p. Doop upon data capture? All 2 -level p. Trees for Sp. S[X X, (x 1 -x 3)2+(x 2 -x 4)2] put in 2 p. Doop. embarrassingly parallelizable E 1 -a, f Eb-e D 1 -f C 1 -5, f 0 0 0 0 0 1 1 0 0 0 pure 1 p 13 1 1 1 1 0 0 0 1 1 1 1 1 0 p 12 p 11 p 10 0 0 1 1 1 1 0 0 1 0 1 1 0 1 1 1 1 0 1 1 p 23 0 0 0 0 0 1 1 1 p 22 0 0 0 0 0 1 0 0 0 p 21 0 0 1 1 0 0 1 1 1 0 p 20 pure 0 1 1 0 1 0 1 1 0 0 0 0 What I'm after here is Sp. SX(d(x, {y X|y x}) and I would like to compute this Sp. S without looping on X. C 6 -e B 1 -f A 1 -6 A 7 -a Ab-f P 131 -f P 121 -f P 111 -f P 101 -f P 231 -f P 221 -f P 211 -f P 201 -f P 331 -f P 321 -f P 311 -f P 301 -f P 431 -f P 421 -f P 411 -f P 401 -f Level-0 ‡ ‡
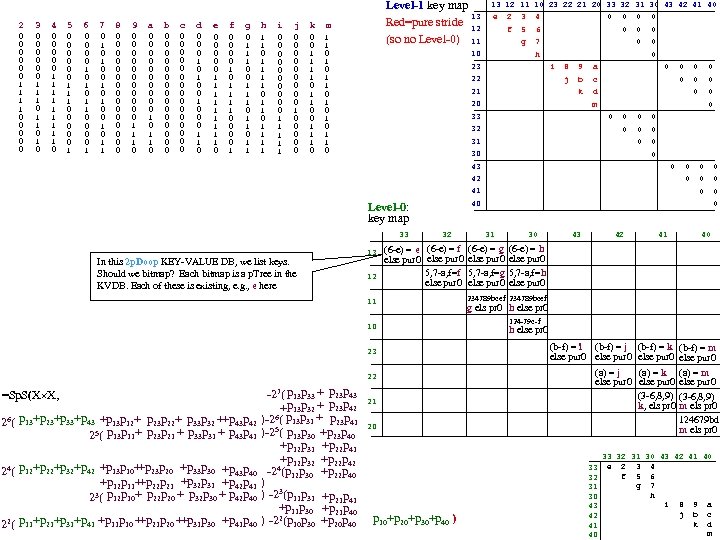2 0 0 0 1 1 0 0 0 3 0 0 0 1 1 1 0 1 0 4 0 0 0 1 1 1 1 1 0 5 0 0 0 1 1 1 0 0 0 1 6 0 0 1 0 1 1 0 0 1 7 0 1 0 1 0 0 1 1 8 0 0 0 0 9 0 0 0 1 1 1 0 a 0 0 0 0 0 1 0 1 1 0 b 0 0 0 0 c 0 0 0 0 d 0 0 0 1 0 0 0 1 1 0 e 0 0 0 1 1 1 1 1 0 f 0 0 1 0 1 1 0 0 1 g 0 1 1 1 0 1 1 h 1 1 0 1 1 i 0 0 0 0 0 1 1 1 j 0 0 0 0 0 1 0 0 0 k 0 0 1 1 0 0 1 1 1 0 Level-1 key map 13 Red=pure stride 12 (so no Level-0) 11 m 1 1 0 1 0 1 0 13 12 11 10 23 22 21 20 33 32 31 30 43 42 41 40 e 10 2 3 4 f 5 6 g 0 0 0 0 7 0 0 h 23 0 i a b c k 21 9 j 22 8 d 20 0 0 0 0 0 31 30 0 0 32 31 (6 -e) = e (6 -e) = f (6 -e) = g else pur 0 5, 7 -a, f=f 5, 7 -a, f=g else pur 0 11 10 23 22 -27( p 13 p 33 + p 23 p 43 +p 13 p 32 + p 23 p 42 6( p p + p p 23 41 26( p 13+p 23+p 33+p 43 +p 13 p 12+ p 23 p 22+ p 33 p 32 ++p 43 p 42 ) -2 13 31 5 25( p 13 p 11+ p 23 p 21 + p 33 p 31 + p 43 p 41 ) -2 ( p 13 p 30 +p 23 p 40 +p 12 p 31 +p 22 p 41 +p 12 p 32 +p 22 p 42 +p 24( p 12+p 22+p 32+p 42 +p 13 p 10+ 23 p 20 +p 33 p 30 +p 43 p 40 -24(p 12 p 30 +p 22 p 40 +p 12 p 11+ 22 p 21 +p 32 p 31 +p 42 p 41 ) +p 3( p 12 p 10+ p 22 p 20 + p 32 p 30 + p 42 p 40 ) -23(p 11 p 31 +p p 2 21 41 +p 11 p 30 +p 21 p 40 2 22( p 11+p 21+p 31+p 41 +p 11 p 10 ++p 21 p 20 ++p 31 p 30 +p 41 p 40 ) -2 (p 10 p 30 +p 20 p 40 0 0 40 Level-0: key map =Sp. S(X X, 0 0 41 0 0 42 12 0 0 0 32 13 0 0 43 In this 2 p. Doop KEY-VALUE DB, we list keys. Should we bitmap? Each bitmap is a p. Tree in the KVDB. Each of these is existing, e. g. , e here 0 0 m 33 0 0 21 20 p 10+p 20+p 30+p 40 ) 0 30 43 42 41 40 (6 -e) = h else pur 0 5, 7 -a, f=h else pur 0 234789 bcef g els pr 0 h else pr 0 124 -79 c-f h else pr 0 (b-f) = i (b-f) = j (b-f) = k (b-f) = m else pur 0 (a) = j (a) = k else pur 0 (3 -6, 8, 9) k, els pr 0 (a) = m else pur 0 (3 -6, 8, 9) m els pr 0 124679 bd m els pr 0 33 32 31 30 43 42 41 40 33 e 2 3 4 f 5 6 32 g 7 31 h 30 i 8 9 a 43 j b c 42 k d 41 m 40
p. Tree Rank(K) 11/17/12 (Rank(n-1) applied to Sp. S(X X, d 2(x, y)) gives 2 nd smallest distance from each x (useful in outlier analysis? ) Rank. Kval=0; p=K; c=0; P=Pure 1; /*Also Rank. Pts are returned as the resulting p. Tree, P*/ For i=n to 0 {c=Count(P&Pi); If (c>=p) {Rank. Val=Rank. Val+2 i; P=P&Pi }; else {p=p-c; P=P&P'i }; return Rank. Kval, P; /* Below K=n-1=7 -1=6 (looking for the 6 th highest = 2 nd lowest value) */ /* Notice that each new P has value. We should retain every one of them. How to catalog in 2 p. Doop? ? */ Cross out the 0 -positions of P each step. X P 4, 3 P 4, 2 P 4, 1 P 4, 0 10 1 0 5 0 1 6 0 1 1 0 7 0 1 11 1 0 1 1 9 1 0 0 1 3 0 0 1 1 (n=3) c=Count(P&P 4, 3)= 3 < 6 p=6– 3=3; P=P&P’ 4, 3 masks off highest 3 (n=2) c=Count(P&P 4, 2)= 3 >= 3 P=P&P 4, 2 masks off lowest 1 (n=1) c=Count(P&P 4, 1)=2 < 3 p=3 -2=1; P=P&P'4, 1 masks off highest 2 (n=0) c=Count(P&P 4, 0 )=1 Rank. Kval= 23 * {0}+ 22 *{1}+ 21 * {0} 20 * {1} = 5 + >= 1 {0} (val 8) {1} (val 4) {0} (val 8 -2=6 ) {1} P=P&P 4, 0 0 1 0 0 0 P=Map. Rank. KPts= List. Rank. KPts={2}
Suppose Min. Val is duplicated (occurs at two points). What does the algorithm return? Rank. Kval=0; p=K; c=0; P=Pure 1; /*Also Rank. Pts are returned as the resulting p. Tree, P*/ For i=n to 0 {c=Count(P&Pi); If (c>=p) {Rank. Val=Rank. Val+2 i; P=P&Pi }; else {p=p-c; P=P&P'i }; ret Rank. Kval, P; P 4, 3 P 4, 2 P 4, 1 P 4, 0 1. P = P 4, 3 10 1 0 5 0 1 Ct (P) = 3 6 0 1 1 0 3 0 0 1 1 P = P’ 4, 3 masks off highest 3 11 1 0 1 1 9 1 0 0 1 3 0 0 1 1 < 6 {0} (Val 8) p=6– 3=3 2. Ct(P&P 4, 2) = 2 <3 {0} P = P&P'4, 2 p=3 -2=1 masks off highest 2 (val 4) 3. Ct(P&P 4, 1 )=2 P=P&P 4, 1 4. Ct (P&P 4, 0 )=1 P=P&P 4, 0 23 * {0}+ 22 *{0}+ 21 * {1} 20 * {1} = + >= 1 {1} 3=Min. Val=rank(n-1)Val. Pmask Min. Pts=rank(n-1)Pts{#4, #7}
Suppose Min. Val is triplicated (occurs at three points). What does the algorithm return? Rank. Kval=0; p=K; c=0; P=Pure 1; /*Also Rank. Pts are returned as the resulting p. Tree, P*/ For i=n to 0 {c=Count(P&Pi); If (c>=p) {Rank. Val=Rank. Val+2 i; P=P&Pi }; else {p=p-c; P=P&P'i }; return Rank. Kval, P; P 4, 3 P 4, 2 P 4, 1 P 4, 0 1. P = P 4, 3 10 1 0 3 0 0 1 1 Ct (P) = 3 6 0 1 1 0 3 0 0 1 1 P = P’ 4, 3 (masks off the highest 3 val 8) 11 1 0 1 1 9 1 0 0 1 3 0 0 1 1 < 6 {0} p=6– 3=3 2. Ct(P&P 4, 2) = 1 <3 {0} P = P&P'4, 2 p=3 -1=2 (masks off highest 1 val 4) 3. Ct(P&P 4, 1 )=3 P=P&P 4, 1 4. Ct (P&P 4, 0 )=3 P=P&P 4, 0 23 * {0}+ 22 *{0}+ 21 * {1} 20 * {1} = 3=Min. Val. + >= 2 {1} Pc mask Min. Pts #4, #5, #7
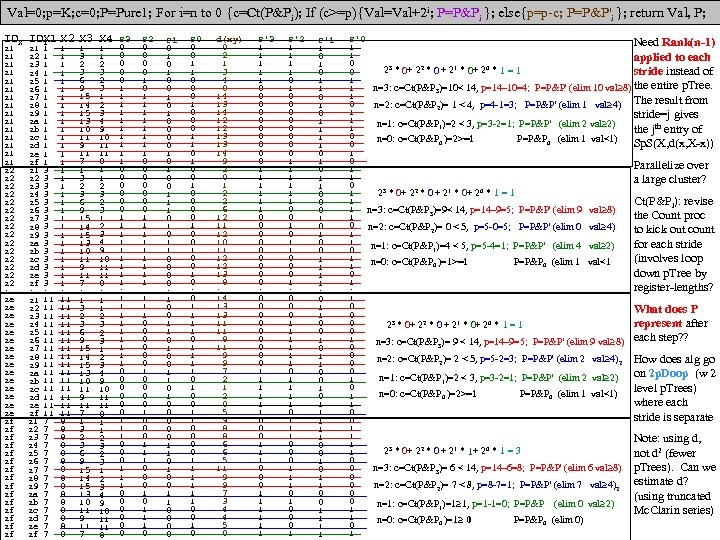Val=0; p=K; c=0; P=Pure 1; For i=n to 0 {c=Ct(P&Pi); If (c>=p){Val=Val+2 i; P=P&Pi }; else{p=p-c; P=P&P'i }; return Val, P; IDX IDY X 2 X 3 X 4 X 1 z 1 z 1 z 1 z 2 z 2 z 2 z 2 z 2 : ze ze ze ze zf zf zf zf z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 za zb zc zd ze zf : z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 za zb zc zd ze zf 1 1 1 1 3 3 3 3 : 11 11 11 11 7 7 7 7 1 1 1 1 1 1 1 1 : 11 11 11 11 8 8 8 8 1 3 2 3 6 9 15 14 15 13 10 11 9 11 7 : 1 3 2 3 6 9 15 14 15 13 10 11 9 11 7 1 1 2 3 2 3 1 2 3 4 9 10 11 11 8 : 1 1 2 3 2 3 1 2 3 4 9 10 11 11 8 P 3 0 0 0 1 1 1 1 1 : 1 1 1 1 1 0 0 0 0 0 0 P 2 0 0 1 0 1 1 1 1 0 0 0 0 1 1 1 0 0 0 1 0 0 0 1 1 1 0 P 1 0 1 0 0 1 1 1 0 0 : 1 0 0 1 1 0 1 0 0 0 1 1 0 0 P 0 0 0 1 1 0 0 1 0 0 1 0 : 0 1 1 1 1 0 1 0 0 1 1 1 0 0 1 0 d(xy) 0 2 1 3 4 8 14 13 14 12 12 13 13 14 9 2 0 1 2 2 6 12 11 12 10 11 12 12 13 8 : 14 13 13 11 11 8 11 9 9 7 2 1 2 0 5 9 8 8 6 6 5 11 9 9 7 3 4 4 5 0 P'3 1 1 1 0 0 0 0 0 : 0 0 0 0 0 1 1 1 1 1 1 P'2 1 1 0 1 0 0 0 0 1 1 1 0 0 0 1 : 0 0 0 1 1 1 0 1 1 1 0 0 0 1 P'1 1 0 1 0 1 1 0 0 0 1 1 : 0 1 1 0 0 1 0 1 1 1 0 0 1 1 P'0 Need Rank(n-1) 1 1 applied to each 0 23 * + 22 * + 21 * + 20 * 1 = 1 0 0 stride instead of 1 n=3: c=Ct(P&P 3)=10< 14, p=14– 10=4; P=P&P' (elim 10 val 8) the entire p. Tree. 1 1 0 n=2: c=Ct(P&P 2)= 1 < 4, p=4 -1=3; P=P&P' (elim 1 val 4) The result from 1 stride=j gives 1 n=1: c=Ct(P&P 1)=2 < 3, p=3 -2=1; P=P&P' (elim 2 val 2) 1 the jth entry of 0 n=0: c=Ct(P&P 0 )=2>=1 P=P&P 0 (elim 1 val<1) Sp. S(X, d(x, X-x)) 0 1 0 Parallelize over 1 1 a large cluster? 0 23 * + 22 * + 21 * + 20 * 1 = 1 1 0 0 0 1 Ct(P&Pi): revise 1 n=3: c=Ct(P&P 3)=9< 14, p=14– 9=5; P=P&P' (elim 9 val 8) the Count proc 1 0 n=2: c=Ct(P&P 2)= 0 < 5, p=5 -0=5; P=P&P' (elim 0 val 4) to kick out count 1 1 for each stride n=1: c=Ct(P&P 1)=4 < 5, p=5 -4=1; P=P&P' (elim 4 val 2) 0 1 (involves loop n=0: c=Ct(P&P 0 )=1>=1 P=P&P 0 (elim 1 val<1 1 down p. Tree by 0 1 register-lengths? : 1 0 What does P 0 0 represent after 23 * + 22 * + 21 * + 20 * 1 = 1 0 0 1 n=3: c=Ct(P&P 3)= 9 < 14, p=14– 9=5; P=P&P' (elim 9 val 8) each step? ? 0 0 n=2: c=Ct(P&P 2)= 2 < 5, p=5 -2=3; P=P&P' (elim 2 val 4)2 How does alg go 0 0 on 2 p. Doop (w 2 n=1: c=Ct(P&P 1)=2 < 3, p=3 -2=1; P=P&P' (elim 2 val 2) 1 0 level p. Trees) n=0: c=Ct(P&P 0 )=2>=1 P=P&P 0 (elim 1 val<1) 1 where each 1 0 stride is separate 0 1 1 Note: using d, 1 23 * + 22 * + 21 * + 20 * 1 = 3 0 0 1 1 not d 2 (fewer 0 n=3: c=Ct(P&P 3)= 6 < 14, p=14– 6=8; P=P&P' (elim 6 val 8) p. Trees). Can we 0 0 0 n=2: c=Ct(P&P 2)= 7 < 8, p=8 -7=1; P=P&P' (elim 7 val 4)2 estimate d? 0 (using truncated 0 n=1: c=Ct(P&P 1)=1 1, p=1 -1=0; P=P&P (elim 0 val 2) 1 Mc. Clarin series) 1 n=0: c=Ct(P&P 0 )=1 0 P=P&P 0 (elim 0) 0 1
Sparse Gap Revealer Width 24 Count 2 11/10/112 on a Sp. S of unknown origin ; -) (can't reconstruct it). X x 1 x 2 f= z 1 1 1 z 2 3 1 z 3 2 2 z 4 3 3 z 5 6 2 z 6 9 3 z 7 15 1 z 8 14 2 z 9 15 3 za 13 4 zb 10 9 zc 11 10 zd 9 11 ze 11 11 zf 7 8 xod 11 27 23 34 53 80 118 114 125 114 110 121 109 125 83 p 6 0 0 0 1 1 1 1 1 p 5 0 0 0 1 1 1 1 1 0 p 4 0 1 1 1 1 0 1 1 p 3 1 1 0 0 0 1 0 1 1 0 p 2 0 0 1 0 1 0 1 1 0 p 1 1 1 0 0 0 1 p 0 1 1 1 0 0 0 1 1 1 1 p 6' 1 1 1 0 0 0 0 0 p 5' 1 1 1 0 0 0 0 0 1 p 4' 1 0 0 0 0 1 0 0 p 3' 0 0 1 1 1 0 1 0 0 1 p 2' 1 1 0 1 0 1 0 0 1 p 1' 0 0 1 1 1 0 p 0' 0 0 0 1 1 1 0 0 0 0 1 z 2 z 7 2 z 3 z 5 z 8 3 z 4 z 6 z 9 4 za 5 M 6 7 8 zf 9 zb a zc b zd ze c 0 1 2 3 4 5 6 7 8 9 a b c d e f p 4' 0 p 6' 0 0 p 5' 1 p 6' &p 5' &p 4' 0 1 1 0 1 [000 0000, 000 1111]= [0, 15]=[0, 16) 1 0 1 1 has 1 point in it, z 1 od=11 is only 0 0 0 1 1 0 5 units from the right edge, so z 1 is 0 1 1 0 0 0 not declared an outlier (yet). 1 0 0 0 Next, we check the min dis from the 1 0 0 right edge of the next interval to see if 0 0 1 1 0 z 1's right-side gap is actually 24 (the 0 0 0 1 calculation of the min a p. Tree process 0 0 1 0 - no x looping required!) 1 C=5 C=3 C=1 p 4' p 6' p 5' 0 0 1 1 1 [001 0000, 001 1111] = [16, 32). The 1 1 0 0 1 [010 0000 , 010 1111] = [32, 48). 0 minimum, z 3 od=23 is 7 units from the 1 0 1 1 1 0 0 z 4 od=34 is within 2 of 32, so z 4 1 left edge, 16, so z 1 has only a 5+7=12 0 1 0 0 0 is not declared an anomaly. 1 unit gap on its right (not a 24 gap). So z 1 0 0 1 1 0 is not declared a 2 4 1 (and is declared a 2 4 0 1 0 0 1 1 0 1 inlier). 1 0 0 0 1 1 0 0 1 1 0 0 C=5 C=2 C=3 C=2 C=1 &p 4' p 6 &p ' p 5' 1 1 0 0 5 0 0 [100 0000 , 100 1111]= [64, 80). 1 1 0 0 1 1 0 This is clearly a 24 gap. But we have 0 0 0 already declared point to the left an 0 0 1 1 outlier and made a subcluster cut! 0 0 1 1 1 1 0 0 0 0 1 1 p 4 p 6 p 5' 0 0 1 1 1 [101 0000 , 101 1111]= [80, 96). 1 0 0 1 1 0 0 0 z 6 od=80, zfod=83 0 1 X 2 d. X 1 X 2 1 0 X 1 X 2 d. X 1 X 2 0 1 z 7 z 8 1. 4 1 z 9 z 10 2. 2 1 z 7 z 9 2. 0 1 0 0 z 9 z 11 7. 8 1 z 7 z 10 3. 6 1 0 0 z 9 z 12 8. 1 1 z 7 z 11 9. 4 1 0 0 z 9 z 13 10. 0 1 1 z 7 z 12 9. 8 0 0 z 9 z 14 8. 9 0 z 7 z 13 11. 7 0 1 1 0 0 z 11 5. 8 0 z 7 z 14 10. 8 0 1 1 z 10 z 12 6. 3 1 z 8 z 9 1. 4 1 0 0 z 13 8. 1 1 z 8 z 10 2. 2 1 C 10 z 8 z 11 8. 1 z 10 z 14 7. 3 C=2 z 8 z 12 8. 5 z 8 z 13 10. 3 z 8 z 14 9. 5 C 10 C=2 C=0 p 4 p 6' p 5 0 0 1 1 1 [011 0000, 011 1111] = [ 48, 64). 1 0 0 1 z 5 od=53 is 19 from z 4 od=34 (>24) 1 0 0 1 1 1 but 11 from 64. But the next int 1 1 [64, 80) is empty z 5 is 27 from its 1 0 0 1 right nbr. z 5 is declared an outlier 1 0 0 1 and we put a subcluster cut thru z 5 1 0 0 1 1 1 [111 0000 , 1111]= [112, 128) 1 0 0 1 z 7 od=118 1 z 8 1 1 od=114 0 0 1 z 9 od=125 1 od=114 0 za 0 C=5 zcod=121 zeod=125 C=2 C=1 No 24 gaps. But we can consult Sp. S(d 2(x, y) for actual distances: p 6 p 4' p 5 1 1 0 0 [110 0000 , 110 1111]= [96, 112). 0 0 zbod=110, zdo 1 d=109. So both 0 0 1 1 {z 6, zf} declared outliers (gap 16 1 1 0 both sides. 0 0 0 1 1 X 2 d. X 1 X 2 0 0 1 1 z 11 z 12 1. 4 0 0 1 1 z 13 2. 2 1 1 z 14 2. 2 1 1 0 0 1 1 z 12 z 13 2. 2 1 1 0 0 z 12 z 14 1. 0 C 10 p 6 p 4 p 5 0 0 0 1 1 0 0 0 Which reveals that there are 1 1 0 0 1 1 no 24 gaps in this 1 1 0 0 1 1 subcluster. 1 1 And, incidentally, it reveals 1 1 1 0 0 a 5. 8 gap between {7, 8, 9, a} 1 1 1 and {b, c, d, e} but that 1 1 0 0 1 1 analysis is messy and the 1 1 gap would be revealed by 0 0 C 10 the next xof. M round on this C=8 C=6 sub-cluster anyway. C=8 C=2 z 13 z 14 2. 0
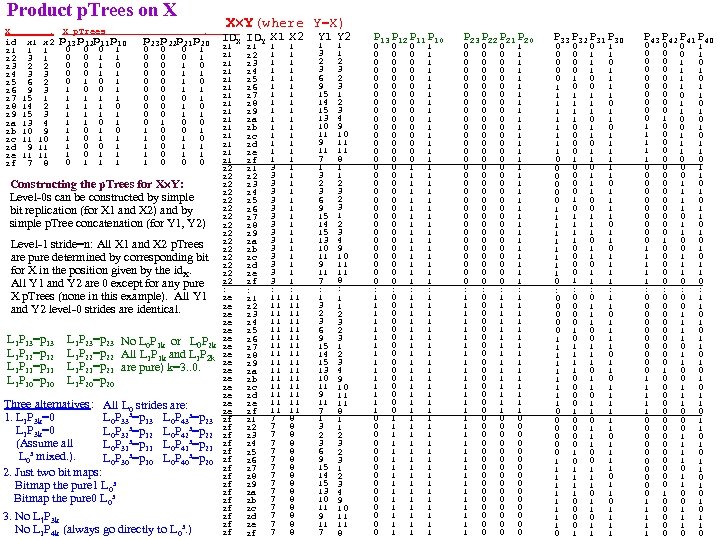Product p. Trees on X X . id x 1 x 2 z 1 1 1 z 2 3 1 z 3 2 2 z 4 3 3 z 5 6 2 z 6 9 3 z 7 15 1 z 8 14 2 z 9 15 3 za 13 4 zb 10 9 zc 11 10 zd 9 11 ze 11 11 zf 7 8 X Y(where Y=X) X p. Trees . p 13 p 12 p 11 p 10 p 23 p 22 p 21 p 20 IDX IDY X 1 X 2 1 1 z 1 z 1 z 1 z 2 z 2 Constructing the p. Trees for X Y: z 2 Level-0 s can be constructed by simple z 2 bit replication (for X 1 and X 2) and by z 2 simple p. Tree concatenation (for Y 1, Y 2) z 2 Level-1 stride=n: All X 1 and X 2 p. Trees z 2 are pure determined by corresponding bit z 2 for X in the position given by the id. X. z 2 All Y 1 and Y 2 are 0 except for any pure z 2 : X p. Trees (none in this example). All Y 1 ze ze and Y 2 level-0 strides are identical. ze ze ze L 1 P 13=p 13 L 1 P 23=p 23 No L 0 P 1 k or L 0 P 2 k ze ze L 1 P 12=p 12 L 1 P 22=p 22 All L 1 P 1 k and L 1 P 2 k ze ze L 1 P 11=p 11 L 1 P 21=p 21 are pure) k=3. . 0. ze ze L 1 P 10=p 10 L 1 P 20=p 20 ze ze ze Three alternatives: All L 0 strides are: ze s=p 1. L 1 P 3 k=0 L 0 P 33 13 L 0 P 43 23 zf L 1 P 3 k=0 L 0 P 32 s=p 12 L 0 P 42 s=p 22 zf zf (Assume all L 0 P 31 s=p 11 L 0 P 41 s=p 21 zf zf L 0 s mixed. ). L 0 P 30 s=p 10 L 0 P 40 s=p 20 zf zf 2. Just two bit maps: zf zf Bitmap the pure 1 L 0 s zf s Bitmap the pure 0 L 0 zf zf zf 3. No L 1 P 3 k zf s. ) No L 1 P 4 k (always go directly to L 0 zf 0 0 0 1 1 1 1 1 0 0 0 1 0 1 1 0 0 1 1 1 0 1 1 1 1 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 1 1 0 0 1 1 1 0 1 0 1 0 1 1 0 z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 za zb zc zd ze zf : z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 za zb zc zd ze zf 1 1 1 1 3 3 3 3 : 11 11 11 11 7 7 7 7 1 1 1 1 1 1 1 1 : 11 11 11 11 8 8 8 8 Y 1 Y 2 1 3 2 3 6 9 15 14 15 13 10 11 9 11 7 : 1 3 2 3 6 9 15 14 15 13 10 11 9 11 7 1 1 2 3 2 3 1 2 3 4 9 10 11 11 8 : 1 1 2 3 2 3 1 2 3 4 9 10 11 11 8 P 13 P 12 P 11 P 10 0 0 0 0 0 0 0 : 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 : 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 : 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 P 23 P 22 P 21 P 20 0 0 0 0 0 0 0 : 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 : 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 : 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 : 1 1 1 1 0 0 0 0 P 33 P 32 P 31 P 30 0 0 1 1 1 1 1 0 : 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 0 1 1 1 1 0 0 0 0 1 : 0 0 0 0 1 0 1 1 1 1 0 0 0 0 1 0 1 1 1 0 1 1 0 1 1 : 0 1 1 1 0 1 1 0 1 1 1 1 0 1 1 1 1 : 1 1 0 1 1 0 1 1 1 1 P 43 P 42 P 41 P 40 0 0 1 1 1 0 0 0 0 0 1 1 1 : 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 0 0 0 0 0 : 0 0 0 0 0 1 0 0 0 0 1 1 1 1 0 0 1 1 1 0 : 0 0 1 1 1 1 0 0 1 1 1 0 1 0 1 0 1 0 1 1 0 : 1 1 0 1 0 1 0 1 1 0
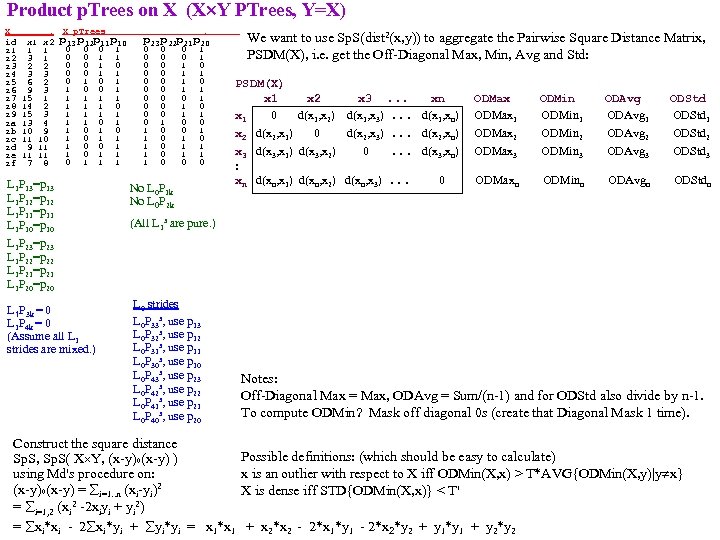Product p. Trees on X (X Y PTrees, Y=X) X . id x 1 x 2 z 1 1 1 z 2 3 1 z 3 2 2 z 4 3 3 z 5 6 2 z 6 9 3 z 7 15 1 z 8 14 2 z 9 15 3 za 13 4 zb 10 9 zc 11 10 zd 9 11 ze 11 11 zf 7 8 X p. Trees . p 13 p 12 p 11 p 10 0 0 1 1 1 1 1 0 0 0 1 0 1 1 0 0 1 1 1 0 1 1 L 1 P 13=p 13 L 1 P 12=p 12 L 1 P 11=p 11 L 1 P 10=p 10 1 1 0 1 1 p 23 p 22 p 21 p 20 0 0 1 1 1 0 0 0 0 0 1 0 0 0 1 1 0 0 1 1 1 0 1 0 1 0 1 1 0 No L 0 P 1 k No L 0 P 2 k We want to use Sp. S(dist 2(x, y)) to aggregate the Pairwise Square Distance Matrix, PSDM(X), i. e. get the Off-Diagonal Max, Min, Avg and Std: PSDM(X) x 1 x 2 x 3. . . xn ODMax ODMin ODAvg ODStd x 1 0 d(x 1, x 2) d(x 1, x 3) . . . d(x 1, xn) ODMax 1 ODMin 1 ODAvg 1 ODStd 1 x 2 d(x 2, x 1) 0 d(x 2, x 3) . . . d(x 2, xn) ODMax 2 ODMin 2 ODAvg 2 ODStd 2 x 3 d(x 3, x 1) d(x 3, x 2) 0 . . . d(x 3, xn) ODMax 3 ODMin 3 ODAvg 3 ODStd 3 : xn d(xn, x 1) d(xn, x 2) d(xn, x 3) . . . 0 ODMaxn ODMinn ODAvgn ODStdn (All L 1 s are pure. ) L 1 P 23=p 23 L 1 P 22=p 22 L 1 P 21=p 21 L 1 P 20=p 20 L 1 P 3 k = 0 L 1 P 4 k = 0 (Assume all L 1 strides are mixed. ) L 0 strides L 0 P 33 s, use p 13 L 0 P 32 s, use p 12 L 0 P 31 s, use p 11 L 0 P 30 s, use p 10 L 0 P 43 s, use p 23 L 0 P 42 s, use p 22 L 0 P 41 s, use p 21 L 0 P 40 s, use p 20 Notes: Off-Diagonal Max = Max, ODAvg = Sum/(n-1) and for ODStd also divide by n-1. To compute ODMin? Mask off diagonal 0 s (create that Diagonal Mask 1 time). Construct the square distance Possible definitions: (which should be easy to calculate) Sp. S, Sp. S( X Y, (x-y)o(x-y) ) x is an outlier with respect to X iff ODMin(X, x) > T*AVG{ODMin(X, y)|y x} using Md's procedure on: 2 (x-y)o(x-y) = i=1. . n (xi-yi) X is dense iff STD{ODMin(X, x)} < T' 2 -2 x y + y 2) = i=1, 2 (xi i = xi*xi - 2 xi*yi + yi*yi = x 1*x 1 + x 2*x 2 - 2*x 1*y 1 - 2*x 2*y 2 + y 1*y 1 + y 2*y 2
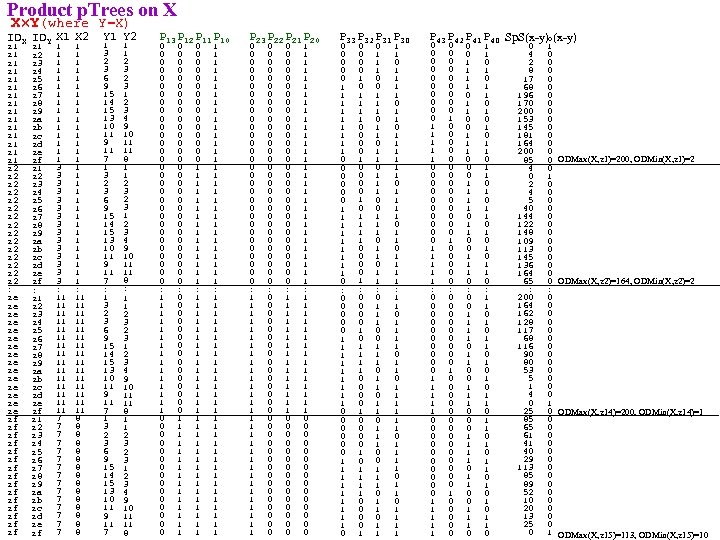Product p. Trees on X X Y(where Y=X) IDX IDY X 1 X 2 z 1 z 1 z 1 z 1 z 2 z 2 z 2 z 2 : ze ze ze ze zf zf zf zf z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 za zb zc zd ze zf : z 1 z 2 z 3 z 4 z 5 z 6 z 7 z 8 z 9 za zb zc zd ze zf 1 1 1 1 3 3 3 3 : 11 11 11 11 7 7 7 7 1 1 1 1 1 1 1 1 : 11 11 11 11 8 8 8 8 Y 1 Y 2 1 3 2 3 6 9 15 14 15 13 10 11 9 11 7 : 1 3 2 3 6 9 15 14 15 13 10 11 9 11 7 1 1 2 3 2 3 1 2 3 4 9 10 11 11 8 : 1 1 2 3 2 3 1 2 3 4 9 10 11 11 8 P 13 P 12 P 11 P 10 0 0 0 0 0 0 0 : 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 : 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 : 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 P 23 P 22 P 21 P 20 0 0 0 0 0 0 0 : 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 : 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 : 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 : 1 1 1 1 0 0 0 0 P 33 P 32 P 31 P 30 0 0 1 1 1 1 1 0 : 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 0 1 1 1 1 0 0 0 0 1 : 0 0 0 0 1 0 1 1 1 1 0 0 0 0 1 0 1 1 1 0 1 1 0 1 1 : 0 1 1 1 0 1 1 0 1 1 1 1 0 1 1 1 1 : 1 1 0 1 1 0 1 1 1 1 P 43 P 42 P 41 P 40 Sp. S(x-y)o(x-y) 0 0 0 0 0 1 1 1 1 1 : 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 1 0 0 0 0 0 : 0 0 0 0 0 1 0 0 0 0 1 1 1 1 0 0 1 1 1 0 : 0 0 1 1 1 1 0 0 1 1 1 0 1 0 1 0 1 0 1 1 0 : 1 1 0 1 0 1 0 1 1 0 0 4 2 8 17 68 196 170 200 153 145 181 164 200 85 4 0 2 4 5 40 144 122 148 109 113 145 136 164 65 : 200 164 162 128 117 68 116 90 80 53 5 1 4 0 25 85 65 61 41 40 29 113 85 89 52 10 20 13 25 0 1 0 0 0 0 0 0 0 : 0 0 0 0 1 0 0 0 0 1 ODMax(X, z 1)=200, ODMin(X, z 1)=2 ODMax(X, z 2)=164, ODMin(X, z 2)=2 ODMax(X, z 14)=200, ODMin(X, z 14)=1 ODMax(X, z 15)=113, ODMin(X, z 15)=10
L 1 P 13 L 1 P 12 L 1 P 11 L 1 P 10 L 0 p 13 L 0 p 12 L 0 p 11 L 0 p 10 0 0 1 1 1 1 1 0 0 0 1 1 1 1 0 0 1 0 1 1 0 1 1 1 1 0 1 1 L 0 P 33 L 0 P 32 L 0 P 31 L 0 P 30 L 1 P 23 L 1 P 22 L 1 P 21 L 1 P 20 L 0 p 23 L 0 p 22 L 0 p 21 L 0 p 20 0 0 1 1 1 0 0 0 0 0 1 1 0 1 1 0 0 1 1 1 0 1 0 1 0 1 1 0 L 0 P 43 L 0 P 42 L 0 P 41 L 0 P 40 L 1(x 1*x 1)=(23 p 13+22 p 12+21 p 11+p 10) = (26(p 13+p 13 p 12)+24(2 p 13 p 11+p 22 p 10+p 13 p 10+p 12 p 11)+23(p 12 p 10)+22 p 11+p 10 L 0(x 1*x 1)= empty L 0(y 2*y 2)=(23 p 13+22 p 12+21 p 11+p 10) = (26(p 13+p 13 p 12)+24(2 p 13 p 11+p 22 p 10+p 13 p 10+p 12 p 11)+23(p 12 p 10)+22 p 11+p 10 L 1(y 2*y 2)= empty L 1 ODMask empty L 0 ODMask=m: m 1 1 0 0 0 0 m 2 0 1 0 0 0 0 . . . mn 0 0 0 0 1 ODMax(X, zk) = Max(L 0(k)[(x-y)o(x-y)] ODMin(X, zk) = Min(L 0(k)[(x-y)o(x-y)*ODMask'], etc. Sp. S( X Y, (x-y)o(x-y) ): (x-y)o(x-y) = i=1. . n (xi-yi)2 = x 1*x 1 + x 2*x 2 - 2*x 1*y 1 - 2*x 2*y 2 + y 1*y 1 + y 2*y 2
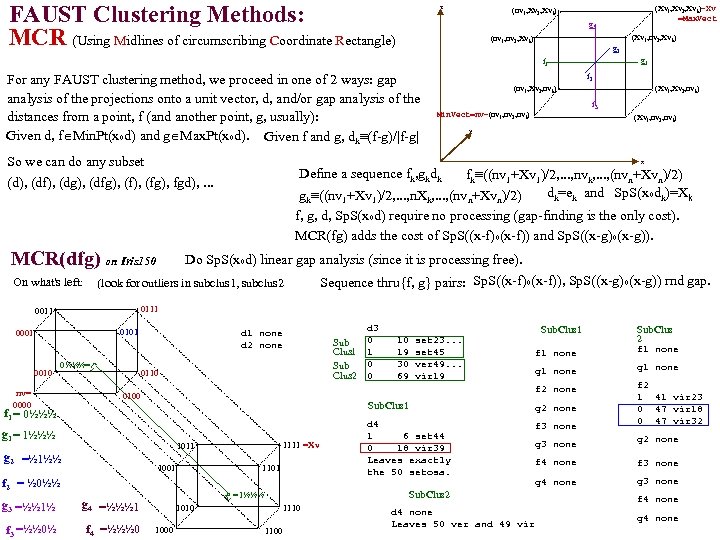FAUST Clustering Methods: MCR (Using Midlines of circumscribing Coordinate Rectangle) z g 3 (Xv 1, nv 2, Xv 3) (nv 1, nv 2, Xv 3) g 2 g 1 f 1 For any FAUST clustering method, we proceed in one of 2 ways: gap analysis of the projections onto a unit vector, d, and/or gap analysis of the distances from a point, f (and another point, g, usually): Given d, f Min. Pt(xod) and g Max. Pt(xod). Given f and g, dk≡(f-g)/|f-g| So we can do any subset (d), (df), (dg), (dfg), (fg), fgd), . . . MCR(dfg) on Iris 150 On what's left: f 2 (Xv 1, Xv 2, nv 3) (nv 1, Xv 2, nv 3) f 3 Min. Vect=nv=(nv 1, nv 2, nv 3) (Xv 1, nv 2, nv 3) y x Define a sequence fk, gkdk fk≡((nv 1+Xv 1)/2, . . . , nvk, . . . , (nvn+Xvn)/2) dk=ek and Sp. S(xodk)=Xk gk≡((nv 1+Xv 1)/2, . . . , n. Xk, . . . , (nvn+Xvn)/2) f, g, d, Sp. S(xod) require no processing (gap-finding is the only cost). MCR(fg) adds the cost of Sp. S((x-f)o(x-f)) and Sp. S((x-g)o(x-g)). Do Sp. S(xod) linear gap analysis (since it is processing free). (look for outliers in subclus 1, subclus 2 Sequence thru{f, g} pairs: Sp. S((x-f)o(x-f)), Sp. S((x-g)o(x-g)) rnd gap. 0111 0011 0½½½=f 1 nv= 0000 d 1 none d 2 none 0110 0100 g 1 = 1½½½ 1111 =Xv 1011 1101 1001 f 2 = ½ 0½½ g 3 =½½ 1½ f 4 =½½½ 0 g =1½½½ 1 g 4 =½½½ 1 f 3 =½½ 0½ Sub Clus 1 Sub Clus 2 f 1 none Sub. Clus 2 f 1 none g 1 none f 2 1 41 vir 23 0 47 vir 18 0 47 vir 32 Sub. Clus 1 f 1 = 0½½½ g 2 =½ 1½½ d 3 0 10 set 23. . . 1 19 set 45 0 30 ver 49. . . 0 69 vir 19 f 2 none 0101 0010 (Xv 1, Xv 2, Xv 3)=Xv =Max. Vect (nv 1, Xv 2, Xv 3) d 4 1 6 set 44 0 18 vir 39 Leaves exactly the 50 setosa. f 3 none g 3 none 1100 g 2 none f 4 none f 3 none g 4 none g 3 none Sub. Clus 2 1110 1000 g 2 none d 4 none Leaves 50 ver and 49 vir f 4 none g 4 none
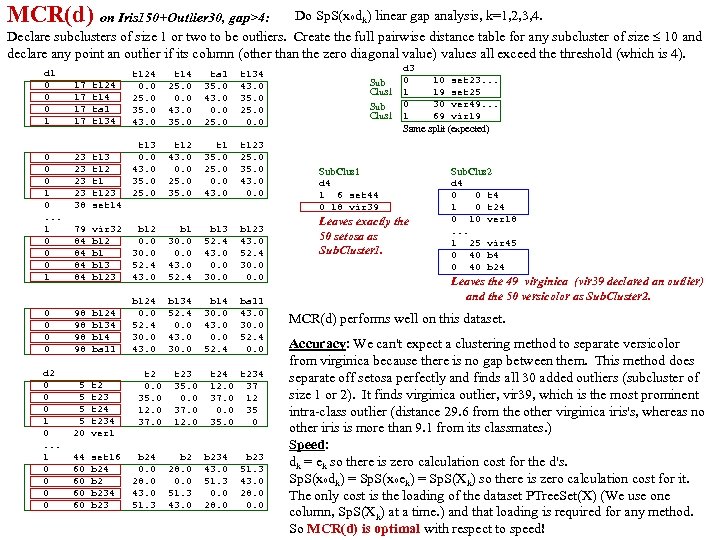MCR(d) on Iris 150+Outlier 30, gap>4: Do Sp. S(xodk) linear gap analysis, k=1, 2, 3, 4. Declare subclusters of size 1 or two to be outliers. Create the full pairwise distance table for any subcluster of size 10 and declare any point an outlier if its column (other than the zero diagonal value) values all exceed the threshold (which is 4). d 1 0 17 t 124 0 17 t 14 0 17 tal 1 17 t 134 0 23 t 13 0 23 t 12 0 23 t 1 1 23 t 123 0 38 set 14. . . 1 79 vir 32 0 84 b 13 1 84 b 123 0 98 b 124 0 98 b 134 0 98 b 14 0 98 ball d 2 0 5 t 23 0 5 t 24 1 5 t 234 0 20 ver 1. . . 1 44 set 16 0 60 b 24 0 60 b 234 0 60 b 23 t 124 t 14 tal t 134 0. 0 25. 0 35. 0 43. 0 25. 0 0. 0 43. 0 35. 0 43. 0 0. 0 25. 0 43. 0 35. 0 25. 0 0. 0 t 13 t 123 0. 0 43. 0 35. 0 25. 0 43. 0 0. 0 25. 0 35. 0 25. 0 0. 0 43. 0 25. 0 35. 0 43. 0 0. 0 b 12 b 13 b 123 0. 0 30. 0 52. 4 43. 0 30. 0 43. 0 52. 4 43. 0 0. 0 30. 0 43. 0 52. 4 30. 0 b 124 b 134 b 14 ball 0. 0 52. 4 30. 0 43. 0 52. 4 0. 0 43. 0 30. 0 43. 0 0. 0 52. 4 43. 0 30. 0 52. 4 0. 0 t 23 t 24 t 234 0. 0 35. 0 12. 0 37 35. 0 0. 0 37. 0 12 12. 0 37. 0 0. 0 35 37. 0 12. 0 35. 0 0 b 24 b 234 b 23 0. 0 28. 0 43. 0 51. 3 28. 0 0. 0 51. 3 43. 0 51. 3 0. 0 28. 0 51. 3 43. 0 28. 0 0. 0 Sub Clus 1 d 3 0 10 set 23. . . 1 19 set 25 0 30 ver 49. . . 1 69 vir 19 Same split (expected) Sub. Clus 1 d 4 1 6 set 44 0 18 vir 39 Leaves exactly the 50 setosa as Sub. Cluster 1. Sub. Clus 2 d 4 0 0 t 4 1 0 t 24 0 10 ver 18. . . 1 25 vir 45 0 40 b 4 0 40 b 24 Leaves the 49 virginica (vir 39 declared an outlier) and the 50 versicolor as Sub. Cluster 2. MCR(d) performs well on this dataset. Accuracy: We can't expect a clustering method to separate versicolor from virginica because there is no gap between them. This method does separate off setosa perfectly and finds all 30 added outliers (subcluster of size 1 or 2). It finds virginica outlier, vir 39, which is the most prominent intra-class outlier (distance 29. 6 from the other virginica iris's, whereas no other iris is more than 9. 1 from its classmates. ) Speed: dk = ek so there is zero calculation cost for the d's. Sp. S(xodk) = Sp. S(xoek) = Sp. S(Xk) so there is zero calculation cost for it. The only cost is the loading of the dataset PTree. Set(X) (We use one column, Sp. S(Xk) at a time. ) and that loading is required for any method. So MCR(d) is optimal with respect to speed!
CCR(fgd) (Corners of Circumscribing Coordinate Rectangle) f 1=min. Vec. X≡(min. Xx 1. . min. Xxn) (0000) g 1=Max. Vec. X≡(Max. Xx 1. . Max. Xxn) (1111), d=(g-f)/|g-f| Sequence thru main diagonal pairs, {f, g} lexicographically. For each, create d. f 1=Mn. Vec Rn. Gp>4 none start Sub Clus 1 Sub Clus 2 g 1=Mx. Vec Rn. Gp>4 0 7 vir 18. . . 1 47 ver 30 0 53 ver 49. . 0 74 set 14 Sub. Clus 1 Lin>4 none f 2=0001 Rn. Gp>4 none CCR(f) Do Sp. S((x-f)o(x-f)) round gap analysis CCR(g) Do Sp. S((x-g)o(x-g)) round gap analysis. CCR(d) Do Sp. S((xod)) linear gap analysis. Notes: No calculation required to find f and g (assuming Max. Vec. X and min. Vec. X have been calculated and residualized when PTree. Set. X was captured. ) Sub. Cluster 2 g 2=1110 Rn. Gp>4 none This ends Sub. Clus 2 = 47 setosa only Lin>4 none f 1=0000 Rn. Gp>4 none g 1=1111 Rn. Gp>4 none Lin>4 none f 3=0010 Rn. Gp>4 none f 2=0001 Rn. Gp>4 none g 2=1110 Rn. Gp>4 none Lin>4 none f 3=0010 Rn. Gp>4 none g 3=1101 Rn. Gp>4 none Lin>4 none f 4=0011 Rn. Gp>4 none g 4=1100 Rn. Gp>4 none Lin>4 none f 5=0100 Rn. Gp>4 none g 5=1011 Rn. Gp>4 none Lin>4 none If the dimension is high, since the main diagonal corners are liekly far from X and thus the large radii make the round gaps nearly linear. g 3=1101 Rn. Gp>4 none g 4=1100 Rn. Gp>4 none Lin>4 none f 5=0100 Rn. Gp>4 none g 5=1011 Rn. Gp>4 none Lin>4 none f 6=0101 Rn. Gp>4 none g 6=1010 Rn. Gp>4 none f 6=0101 Rn. Gp>4 1 19 set 26 0 28 ver 49 0 31 set 42 0 31 ver 8 0 32 set 36 0 32 ver 44 1 35 ver 11 0 41 ver 13 ver 49 set 42 ver 8 set 36 ver 44 ver 11 0. 0 19. 8 3. 9 21. 3 3. 9 7. 2 19. 8 0. 0 21. 6 10. 4 21. 8 23. 8 3. 9 21. 6 0. 0 23. 9 1. 4 4. 6 21. 3 10. 4 23. 9 0. 0 24. 2 27. 1 3. 9 21. 8 1. 4 24. 2 0. 0 3. 6 7. 2 23. 8 4. 6 27. 1 3. 6 0. 0 Lin>4 none f 7=0110 Rn. Gp>4 none g 7=1001 Rn. Gp>4 none Lin>4 none f 8=0111 Rn. Gp>4 none f 7=0110 Rn. Gp>4 1 28 ver 13 0 33 vir 49 f 8=0111 Rn. Gp>4 none g 6=1010 Rn. Gp>4 none g 7=1001 Rn. Gp>4 none g 8=1000 Rn. Gp>4 none Lin>4 none This ends Sub. Clus 1 = 95 ver and vir samples only Lin>4 none Subc 2. 1 ver 49 ver 8 ver 44 ver 11
SL SW PL PW 1 set 51 35 14 2 0 1 1 0 0 1 1 1 0 0 0 1 0 2 set 49 30 14 2 0 1 1 0 0 0 1 1 1 1 0 0 0 0 0 1 0 3 set 47 32 13 2 0 1 1 1 0 0 0 0 1 0 4 set 46 31 15 2 0 1 1 1 0 0 0 1 1 0 0 1 0 5 set 50 36 14 2 0 1 1 0 0 0 1 1 1 0 0 0 1 0 6 set 54 39 17 4 0 1 1 0 1 0 0 1 1 1 0 0 0 1 0 0 7 set 46 34 14 3 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 8 set 50 34 15 2 0 1 1 0 0 0 1 0 0 1 0 9 set 44 29 14 2 0 1 1 0 0 0 1 0 10 set 49 31 15 1 0 1 1 0 0 0 1 1 1 1 1 0 0 0 0 0 1 1 set 54 37 15 2 0 1 1 0 1 0 1 0 0 0 1 1 0 0 1 0 2 set 48 34 16 2 0 1 1 0 0 0 1 0 0 0 0 1 0 3 set 48 30 14 1 0 1 1 0 0 1 1 1 0 0 0 1 4 set 43 30 11 1 0 1 0 1 1 1 1 0 0 1 0 1 1 0 0 0 1 5 set 58 40 12 2 0 1 1 1 0 1 0 0 0 0 1 1 0 0 0 1 0 6 set 57 44 15 4 0 1 1 1 0 0 0 1 1 0 0 0 1 0 0 7 set 54 39 13 4 0 1 1 0 1 0 0 1 1 1 0 0 0 1 0 0 8 set 51 35 14 3 0 1 1 0 0 1 1 1 0 0 0 1 1 9 set 57 38 17 3 0 1 1 1 0 0 0 1 0 0 1 1 20 set 51 38 15 3 0 1 1 0 0 0 0 1 1 1 set 54 34 17 2 0 1 1 0 1 0 0 0 0 1 0 2 set 51 37 15 4 0 1 1 0 0 1 0 1 0 0 0 1 0 0 3 set 46 36 10 2 0 1 1 1 0 0 0 0 0 1 0 4 set 51 33 17 5 0 1 1 0 0 1 0 0 0 1 5 set 48 34 19 2 0 1 1 0 0 0 1 0 0 1 0 6 set 50 30 16 2 0 1 1 0 0 0 1 0 0 0 0 1 0 7 set 50 34 16 4 0 1 1 0 0 0 1 0 0 0 0 1 0 0 8 set 52 35 15 2 0 1 1 0 0 0 1 1 1 1 0 0 1 0 9 set 52 34 14 2 0 1 1 0 0 0 0 1 1 1 0 0 0 1 0 30 set 47 32 16 2 0 1 1 1 0 0 0 0 1 0 1 set 48 31 16 2 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 0 2 set 54 34 15 4 0 1 1 0 1 0 0 0 0 1 1 0 0 0 1 0 0 3 set 52 41 15 1 0 1 0 0 1 0 0 0 1 4 set 55 42 14 2 0 1 1 1 1 0 1 0 0 1 1 1 0 0 0 1 0 5 set 49 31 15 1 0 1 1 0 0 0 1 1 1 1 1 0 0 0 0 0 1 6 set 50 32 12 2 0 1 1 0 0 0 0 1 1 0 0 0 1 0 7 set 55 35 13 2 0 1 1 1 1 0 0 0 0 1 0 8 set 49 31 15 1 0 1 1 0 0 0 1 1 1 1 1 0 0 0 0 0 1 9 set 44 30 13 2 0 1 1 0 0 1 1 0 0 0 0 1 0 40 set 51 34 15 2 0 1 1 0 0 1 1 1 0 0 0 0 1 1 0 0 1 0 1 set 50 35 13 3 0 1 1 0 0 0 1 1 0 1 0 0 1 1 2 set 45 23 13 3 0 1 1 0 1 0 1 1 1 0 0 0 0 1 1 3 set 44 32 13 2 0 1 1 0 0 0 0 1 0 4 set 50 35 16 6 0 1 1 0 0 0 1 1 0 0 0 0 0 1 1 0 5 set 51 38 19 4 0 1 1 0 0 0 1 1 0 0 0 1 0 0 6 set 48 30 14 3 0 1 1 0 0 1 1 1 0 0 0 1 1 7 set 51 38 16 2 0 1 1 0 0 0 0 0 0 1 0 8 set 46 32 14 2 0 1 1 1 0 0 0 0 0 1 1 1 0 0 0 1 0 9 set 53 37 15 2 0 1 1 0 0 1 0 0 0 1 1 0 0 1 0 50 set 50 33 14 2 0 1 1 0 0 1 0 0 0 1 1 1 0 0 0 1 ver 70 32 47 14 1 0 0 0 1 1 0 0 0 0 1 1 1 1 0 0 1 1 1 0 2 ver 64 32 45 15 1 0 0 0 1 0 1 0 0 1 1 3 ver 69 31 49 15 1 0 0 0 1 0 1 1 0 0 0 1 1 1 1 4 ver 55 23 40 13 0 1 1 1 0 1 0 0 0 1 1 0 1 ver 65 28 46 15 1 0 0 0 1 0 1 1 1 0 0 0 1 1 5 ver 57 28 45 13 0 1 1 1 0 0 0 1 1 0 1 6 ver 63 33 47 16 0 1 1 1 1 0 0 1 0 1 0 0 7 ver 49 24 33 10 0 1 1 0 0 0 0 1 0 8 ver 66 29 46 13 1 0 0 1 1 1 0 1 0 1 1 1 0 0 0 1 1 0 1 9 ver 52 27 39 14 0 1 1 0 0 0 1 1 0 1 0 0 1 1 1 0 10 ver 50 20 35 10 0 1 1 0 0 0 1 0 0 0 1 1 0 0 1 0 1 ver 59 30 42 15 0 1 1 1 0 0 1 0 1 0 0 0 1 1 2 ver 60 22 40 10 0 1 1 0 0 1 0 0 0 1 0 3 ver 61 29 47 14 0 1 1 1 0 1 0 1 1 0 0 1 1 1 0 4 ver 56 29 36 13 0 1 1 1 0 1 0 0 0 0 1 1 0 1 5 ver 67 31 44 14 1 0 0 1 1 1 0 1 1 0 0 1 1 1 0 6 ver 56 30 45 15 0 1 1 1 0 0 1 1 0 0 1 1 7 ver 58 27 41 10 0 1 1 1 0 0 1 1 0 1 0 1 0 8 ver 62 22 45 15 0 1 1 1 0 0 1 0 1 1 0 0 1 1 9 ver 56 25 39 11 0 1 1 1 0 0 1 0 0 1 1 20 ver 59 32 48 18 0 1 1 1 0 0 0 1 0 1 ver 61 28 40 13 0 1 1 1 0 0 0 1 1 0 1 2 ver 63 25 49 15 0 1 1 1 0 0 1 1 0 0 0 1 1 1 1 3 ver 61 28 47 12 0 1 1 1 0 0 0 1 1 1 1 0 0 4 ver 64 29 43 13 1 0 0 0 0 1 1 1 0 1 0 1 1 0 1 5 ver 66 30 44 14 1 0 0 1 1 0 0 1 1 1 0 6 ver 68 28 48 14 1 0 0 0 1 1 1 0 0 0 1 1 1 0 7 ver 67 30 50 17 1 0 0 1 1 0 0 1 1 0 0 0 1 8 ver 60 29 45 15 0 1 1 0 0 0 1 1 1 0 1 0 1 0 0 1 1 9 ver 57 26 35 10 0 1 1 1 0 0 1 0 0 0 1 1 0 0 1 0 30 ver 55 24 38 11 0 1 1 1 0 0 0 0 1 1 1 ver 55 24 37 10 0 1 1 1 0 0 1 0 1 0 2 ver 58 27 39 12 0 1 1 1 0 0 1 1 0 0 3 ver 60 27 51 16 0 1 1 0 0 0 1 1 0 1 0 0 4 ver 54 30 45 15 0 1 1 0 0 1 1 0 0 1 1 5 ver 60 34 45 16 0 1 1 0 0 1 1 0 1 0 0 6 ver 67 31 47 15 1 0 0 1 1 1 0 1 1 0 0 1 1 7 ver 63 23 44 13 0 1 1 1 0 1 1 0 1 8 ver 56 30 41 13 0 1 1 1 0 0 1 0 0 1 1 0 1 9 ver 55 25 40 13 0 1 1 1 0 0 1 0 1 0 0 0 1 1 0 1 40 ver 55 26 44 12 0 1 1 1 0 1 0 0 1 1 0 0 1 ver 61 30 46 14 0 1 1 1 1 0 0 1 1 1 0 2 SL SW PL PW ver 58 26 40 12 0 1 1 1 0 1 0 0 0 1 1 0 0 3 ver 50 23 33 10 0 1 1 0 0 1 0 1 1 1 0 0 0 0 1 0 1 0 4 ver 56 27 42 13 0 1 1 1 0 0 1 1 0 1 0 1 0 0 0 1 1 0 1 5 ver 57 30 42 12 0 1 1 1 0 0 1 0 1 0 1 0 0 0 1 1 0 0 6 ver 57 29 42 13 0 1 1 1 0 1 0 1 0 0 0 1 1 0 1 7 ver 62 29 43 13 0 1 1 1 0 1 0 1 1 0 1 8 ver 51 25 30 11 0 1 1 0 0 1 1 0 0 0 1 1 9 ver 57 28 41 13 0 1 1 1 0 0 0 1 1 0 1 50 1 vir 63 33 60 25 0 1 1 1 1 0 0 1 0 1 1 0 0 1 2 vir 58 27 51 19 0 1 1 1 0 0 1 1 0 1 0 0 1 1 3 vir 71 30 59 21 1 0 0 0 1 1 1 1 0 0 1 1 1 0 1 0 1 4 vir 63 29 56 18 0 1 1 1 0 1 1 1 0 0 1 0 5 vir 65 30 58 22 1 0 0 0 1 1 1 1 0 0 1 1 0 6 vir 76 30 66 21 1 0 0 0 1 1 0 1 0 0 1 0 1 7 vir 49 25 45 17 0 1 1 0 0 1 0 1 0 0 0 1 8 vir 73 29 63 18 1 0 0 1 0 1 1 1 0 1 0 9 vir 67 25 58 18 1 0 0 1 1 1 0 0 1 0 10 vir 72 36 61 25 1 0 0 0 1 1 0 0 1 1 vir 65 32 51 20 1 0 0 0 0 0 1 1 0 1 0 0 2 vir 64 27 53 19 1 0 0 0 0 1 1 0 1 0 0 1 1 3 vir 68 30 55 21 1 0 0 0 1 1 1 0 1 0 1 4 vir 57 25 50 20 0 1 1 1 0 0 1 0 0 5 vir 58 28 51 24 0 1 1 1 0 0 0 1 1 0 0 0 6 vir 64 32 53 23 1 0 0 0 1 1 0 1 0 1 1 1 7 vir 65 30 55 18 1 0 0 0 1 1 1 1 0 0 1 0 8 vir 77 38 67 22 1 0 0 1 1 0 1 1 0 9 vir 77 26 69 23 1 0 0 1 1 0 1 0 1 0 0 0 1 0 1 1 1 20 vir 60 22 50 15 0 1 1 0 0 1 0 0 0 1 1 1 vir 69 32 57 23 1 0 0 0 1 1 1 0 0 1 0 1 1 1 2 vir 56 28 49 20 0 1 1 1 0 0 0 1 0 1 0 0 3 vir 77 28 67 20 1 0 0 1 1 1 0 0 0 0 1 1 0 1 0 0 4 vir 63 27 49 18 0 1 1 1 0 1 1 0 0 0 1 0 5 vir 67 33 57 21 1 0 0 0 0 1 0 1 1 1 0 0 1 0 1 6 vir 72 32 60 18 1 0 0 0 1 1 0 0 0 1 0 7 vir 62 28 48 18 0 1 1 1 0 0 0 0 0 1 0 8 vir 61 30 49 18 0 1 1 1 1 0 0 0 1 0 9 vir 64 28 56 21 1 0 0 0 0 1 0 1 30 vir 72 30 58 16 1 0 0 0 0 1 1 1 0 0 1 vir 74 28 61 19 1 0 0 1 1 1 0 0 0 1 1 0 1 0 0 1 1 2 vir 79 38 64 20 1 0 0 1 1 0 0 0 0 1 0 0 3 vir 64 28 56 22 1 0 0 0 0 1 1 0 4 vir 63 28 51 15 0 1 1 1 0 0 0 1 1 5 vir 61 26 56 14 0 1 1 0 0 1 1 1 0 6 vir 77 30 61 23 1 0 0 1 1 0 1 0 1 1 1 7 vir 63 34 56 24 0 1 1 1 1 0 0 0 1 1 1 0 0 0 8 vir 64 31 55 18 1 0 0 0 0 1 1 1 0 0 1 0 9 vir 60 30 18 18 0 1 1 1 1 0 0 0 1 0 40 vir 69 31 54 21 1 0 0 0 1 0 1 1 0 0 1 0 1 1 vir 67 31 56 24 1 0 0 1 1 1 0 0 1 1 0 0 0 2 vir 69 31 51 23 1 0 0 0 1 0 1 1 0 1 0 1 1 1 3 vir 58 27 51 19 0 1 1 1 0 0 1 1 0 1 0 0 1 1 4 vir 68 32 59 23 1 0 0 0 1 1 1 0 1 0 1 1 1 5 vir 67 33 57 25 1 0 0 1 1 1 0 0 1 1 0 0 1 6 vir 67 30 52 23 1 0 0 1 1 0 0 1 1 0 0 0 1 1 1 7 vir 63 25 50 19 0 1 1 1 0 0 1 0 0 1 1 8 vir 65 30 52 20 1 0 0 0 1 1 1 1 0 0 0 1 0 0 9 vir 62 34 54 23 0 1 1 1 0 0 0 1 1 0 0 1 1 1 50 vir 59 30 51 18 0 1 1 1 0 0 1 1 0 1 0 t 1 20 30 37 12 0 0 1 0 0 0 1 1 0 0 1 0 1 0 1 1 t 2 58 5 37 12 0 1 1 1 0 0 0 0 1 0 1 1 t 3 58 30 2 12 0 1 1 1 0 0 0 1 0 0 0 1 1 t 4 58 30 37 0 0 1 1 1 0 0 1 0 1 0 0 0 t 12 20 5 37 12 0 0 1 0 1 0 0 1 0 1 1 t 13 20 30 2 12 0 0 1 0 0 0 1 0 0 0 1 1 t 14 20 30 37 0 0 0 1 1 0 0 1 0 1 0 0 0 t 23 58 5 2 12 0 1 1 1 0 1 0 0 0 0 0 1 1 t 24 58 5 37 0 0 1 1 1 0 0 0 0 1 0 1 0 1 0 0 0 t 34 58 30 2 0 0 1 1 1 0 0 0 1 0 0 0 0 t 123 20 5 2 12 0 0 1 0 1 0 0 0 0 0 1 0 1 1 t 124 20 5 37 0 0 0 1 0 1 0 1 0 0 0 t 134 20 30 2 0 0 0 1 1 0 0 0 0 t 234 58 5 2 0 0 1 1 1 0 1 0 0 0 0 tall 20 5 2 0 0 0 1 0 1 0 0 0 0 b 1 90 30 37 12 1 0 1 0 0 1 0 1 0 1 1 b 2 58 60 37 12 0 1 1 1 0 0 0 1 0 1 0 1 1 b 3 58 30 80 12 0 1 1 1 0 0 1 1 0 1 0 0 0 1 0 1 1 b 4 58 30 37 40 0 1 1 1 0 0 1 0 1 1 0 0 0 b 12 90 60 37 12 1 0 1 0 1 1 0 0 0 1 0 1 0 1 1 b 13 90 30 80 12 1 0 1 0 0 1 1 0 1 0 0 0 1 0 1 1 b 14 90 30 37 40 1 1 0 0 1 0 1 1 0 0 0 b 23 58 60 80 12 0 1 1 1 0 0 1 0 0 0 1 0 1 1 b 24 58 60 37 40 0 1 1 1 0 0 0 1 0 1 1 0 0 0 b 34 58 30 80 40 0 1 1 1 0 0 1 1 0 1 0 1 0 0 0 b 123 90 60 80 12 1 0 1 0 1 1 0 0 0 1 0 1 1 b 124 90 60 37 40 1 0 1 1 1 1 0 0 0 1 0 1 1 0 0 0 b 134 90 30 80 40 1 1 0 1 0 1 0 0 0 b 234 58 60 80 40 0 1 1 1 0 0 1 0 1 0 0 0 ball 90 60 80 40 1 0 1 1 1 1 0 0 1 0 1 0 0 0 Before adding the new tuples: MINS 43 20 10 1 MAXS 79 44 69 25 MEAN 58 30 37 12 same after additions.
FM(fgd) (Furthest-from-the-Mediod) f=M Gp>4 1 53 b 13 0 58 t 123 0 59 b 234 0 59 tal 0 60 b 134 1 61 b 123 0 67 ball DISTANCES t 123 b 234 tal b 134 b 123 0. 00 106. 48 12. 00 111. 32 118. 36 106. 48 0. 00 110. 24 43. 86 42. 52 12. 00 110. 24 0. 00 114. 93 118. 97 111. 32 43. 86 114. 93 0. 00 41. 04 118. 36 42. 52 118. 97 41. 04 0. 00 All outliers! f 0=t 123 Rn. Gp>4 Sub. Clust-1 f 0=b 2 Rn. Gp>4 1 0 b 2 0 28 ver 36 Sub. Clust-2 f 0=t 3 Rn. Gp>4 none Sub. Clust-1 f 0=b 3 Rn. Gp>4 1 0 b 3 0 23 vir 8. . . 1 54 b 1 0 62 vir 39 Sub. Clust-2 f 0=t 3 Lin. Gap>4 1 0 t 3 0 12 t 34 Sub. Clust-1 f 0=t 24 Rn. Gp>4 1 0 t 24 1 12 t 2 0 20 ver 13 Sub. Clust-1 f 0=b 1 Rn. Gp>4 1 0 b 1 0 23 ver 1 Sub. Clust-1 f 0=ver 19 Rn. Gp>4 none Sub. Clust-1 f 0=ver 19 Lin. Gp>4 none Sub. Clust-2 f 0=t 34 Lin. Gap>4 1 0 t 34 0 13 set 36 1 0 t 123 0 25 t 13 1 28 t 134 0 34 set 42. . . 1 103 b 23 0 108 b 13 f 0=b 23 Rn. Gp>4 1 0 b 23 0 30 b 3. . . 1 84 t 34 0 95 t 23 0 96 t 234 FMO (FM using a Gram-Schmidt Orthonormal basis) X Rn. Calculate M=Mean. Vector(X) directly, using only the residualized 1 -counts of the basic p. Trees of X. And BTW, use residualized STD calculations to guide in choosing good gap width thresholds (which define what an outlier is going to be and also determine when we divide into sub-clusters. )) f 1 Mx. Pt(Sp. S[(M-x)o(M-x)]). d 1≡(M-f 1)/|M-f 1|. If d 11 0, Gram-Schmidt {d 1 e 1. . . ek-1 ek+1. . en} d 2 ≡ (e 2 - (e 2 od 1) / |e 2 - (e 2 od 1)d 1| d 3 ≡ (e 3 - (e 3 od 1)d 1 - (e 3 od 2) / |e 3 - (e 3 od 1)d 1 - (e 3 od 2)d 2|. . . dh≡(eh-(ehod 1)d 1 -(ehod 2)d 2 -. . -(ehodh-1) / |eh-(ehod 1)d 1 -(ehod 2)d 2 -. . . -(ehodh-1)dh-1| Thm: Mx. Pt[Sp. S((M-x)od)]=Mx. Pt[Sp. S(xod)] (shift by Mod, Mx. Pts are same Repick f 1 Mn. Pt[Sp. S(xod 1)]. Pick g 1 Mx. Pt[Sp. S(xod 1)] Pick fh Mn. Pt[Sp. S(xodh)]. Pick gh Mx. Pt[Sp. S(xodh)]. f 0=b 124 Rn. Gp>4 1 0 b 124 b 12 b 14 b 24 0 28 b 12 0. 00 41. 04 42. 52 0 30 b 14 41. 04 0. 00 43. 86 1 32 b 24 42. 52 43. 86 0. 00 Sub. Clust-2 f 0=set 16 Ln. Gp>4 none 0 41 vir 10. . . All outliers again! 1 75 t 24 Sub. Clust-1 1 81 t 1 f 1=ver 49 Rd. Gp>4 none 1 86 t 14 Sub. Clust-2 Sub. Clust-1 f 1=set 42 Rd. Gp>4 none 1 93 t 12 f 1=ver 49 Ln. Gp>4 none 0 98 t 124 Sub. Clust-2 f 0=b 34 Rn. Gp>4 f 1=set 42 Ln. Gp>4 none 1 0 b 34 Sub. Clust-2 is 50 setosa! 0 26 vir 1 Likely f 2, f 3 and f 4 . . . Sub. Clust-1 analysis will not find none. 1 66 vir 39 0 72 set 24. . . 1 83 t 3 0 88 t 34 Sub. Clust-2 1. Choose f 0 (high outlier potential? e. g. , furthest from mean, M? ) 2. Do f 0 -rnd-gap analysis (+ subcluster anal? ) 3. f 1 be s. t. no x further away from f 0 (in some dir) (all d 1 dot prods 0) 4. Do f 1 -rnd-gap analysis (+ subclust anal? ). 5. Do d 1 -linear-gap analysis, d 1≡ f 0 -f 1 / |f 0 -f 1|. 6. Let f 2 s. t. no x is further away (in some direction) from d 1 -line than f 2 7. Do f 2 -round-gap analysis. 8. Do d 2 -linear-gap d 2 ≡ f 0 -f 2 - (f 0 -f 2)od 1 / len. . .
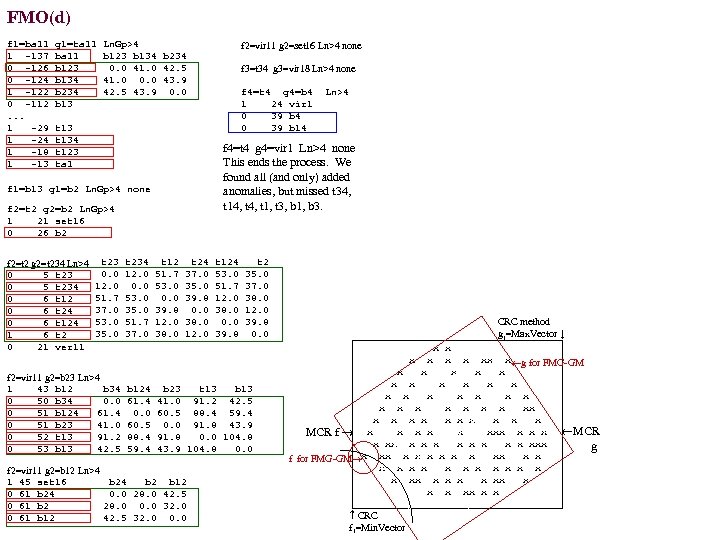FMO(d) f 1=ball g 1=tall Ln. Gp>4 b 123 b 134 b 234 1 -137 ball 0. 0 41. 0 42. 5 0 -126 b 123 41. 0 0. 0 43. 9 0 -124 b 134 42. 5 43. 9 0. 0 1 -122 b 234 0 -112 b 13. . . 1 -29 t 13 1 -24 t 134 1 -18 t 123 1 -13 tal f 1=b 13 g 1=b 2 Ln. Gp>4 none f 2=t 2 g 2=b 2 Ln. Gp>4 1 21 set 16 0 26 b 2 f 2=vir 11 g 2=set 16 Ln>4 none f 3=t 34 g 3=vir 18 Ln>4 none f 4=t 4 g 4=b 4 Ln>4 1 24 vir 1 0 39 b 4 0 39 b 14 f 4=t 4 g 4=vir 1 Ln>4 none This ends the process. We found all (and only) added anomalies, but missed t 34, t 14, t 1, t 3, b 1, b 3. f 2=t 2 g 2=t 234 Ln>4 t 234 t 12 t 24 t 124 t 2 0. 0 12. 0 51. 7 37. 0 53. 0 35. 0 0 5 t 234 12. 0 0. 0 53. 0 35. 0 51. 7 37. 0 51. 7 53. 0 0. 0 39. 8 12. 0 38. 0 0 6 t 12 37. 0 35. 0 39. 8 0. 0 38. 0 12. 0 0 6 t 24 0 6 t 124 53. 0 51. 7 12. 0 38. 0 0. 0 39. 8 35. 0 37. 0 38. 0 12. 0 39. 8 0. 0 1 6 t 2 0 21 ver 11 f 2=vir 11 g 2=b 23 Ln>4 b 34 b 124 b 23 t 13 b 13 1 43 b 12 0 50 b 34 0. 0 61. 4 41. 0 91. 2 42. 5 0 51 b 124 61. 4 0. 0 60. 5 88. 4 59. 4 0 51 b 23 41. 0 60. 5 0. 0 91. 8 43. 9 91. 2 88. 4 91. 8 0. 0 104. 8 0 52 t 13 0 53 b 13 42. 5 59. 4 43. 9 104. 8 0. 0 f 2=vir 11 g 2=b 12 Ln>4 1 45 set 16 0 61 b 24 0 61 b 2 0 61 b 12 b 24 b 2 b 12 0. 0 28. 0 42. 5 28. 0 0. 0 32. 0 42. 5 32. 0 0. 0 CRC method g 1=Max. Vector ↓ x x x x xx x g for FMG-GM x x x x x x x x x x x x x x x x x x xx x x x x x x x x x x xxx x MCR f x x xx x x xxx g xx x x f for FMG-GM x xx x x x x x x x x xx x x xx x xx x x x x x x CRC x xx f 1=Min. Vector x x
f 1=bal Rn. Gp>4 Finally we would classify within Sub. Cluster 1 using the means of another training set (with 1 0 ball FAUST Classify). We would also classify Sub. Cluster 2. 1 and Sub. Cluster 2. 2, but would we know Sub 0 28 b 123. . . we would find Sub. Cluster 2. 1 to be all Setosa and Sub. Cluster 2. 2 to be all Versicolor (as we did Clus 1 1 73 t 4 before). In Sub. Cluster 1 we would separate Versicolor from Virginica perfectly (as we did before). Sub 0 78 vir 39. . . f 1 Mx. Pt(Sp. S((MClus 2 1 98 t 34 t 12 t 23 t 124 t 234 We could FAUST Classify each outlier (if so desired) to find out 0 103 t 12 0. 0 51. 7 12. 0 53. 0 x)o(M-x))), which class they are outliers from. However, what about the rouge 0 104 t 23 51. 7 0. 0 53. 0 12. 0 Round gaps first, outliers I added? What would we expect? They are not represented in 0 107 t 124 12. 0 53. 0 0. 0 51. 7 then Linear gaps. 1 108 t 234 53. 0 12. 0 51. 7 0. 0 the training set, so what would happen to them? My thinking: they 0 113 t 13 are real iris samples so we should not do the really do the outlier 1 116 t 134 analysis and subsequent classification on the original 150. 0 122 t 123 Sub. Clus 2 f 1=t 14 Rn>4 0 125 tal 0 0 t 1 We already know (assuming the "other training set" has the same 1 0 t 14 Sub. Clus 1 f 1=b 123 Rn>4 means as these 150 do), that we can separate Setosa, Versicolor and 0 30 ver 8. . . 1 0 b 123 b 13 vir 32 vir 18 b 23 Virginica prefectly using FAUST Classify. 1 47 set 15 0 30 b 13 0. 0 22. 5 22. 4 43. 9 0 52 t 3 0 30 vir 32 22. 5 0. 0 4. 1 35. 3 0 52 t 34 0 30 vir 18 If this is typical (though concluding 22. 4 4. 1 0. 0 33. 4 1 32 b 23 43. 9 35. 3 33. 4 0. 0 from one example is definitely "over 0 37 vir 6 Sub. Clus 2 f 1=set 23 Rn>4 FMO(fg) start Sub. Clus 1 f 1=b 134 Rn>4 1 0 b 134 0 24 vir 19 SC 1 f 2=ver 13 Rn>4 1 0 ver 13 0 5 ver 43 Sub. Clus 1 f 1=b 234 Rn>4 SC 1 g 2=vir 10 Rn>4 1 0 b 234 1 0 vir 10 1 30 b 34 0 6 vir 44 0 37 vir 10 Sub. Clus 1 f 1=b 124 Rn>4 b 12 b 14 1 0 b 124 0. 0 28. 0 30. 0 0 28 b 12 28. 0 0. 0 41. 0 0 30 b 14 30. 0 41. 0 0. 0 1 32 b 24 0 41 b 1. . . SC 1 f 4=b 1 Rn>4 1 59 t 4 1 0 b 1 0 68 b 3 0 23 ver 1 1 17 vir 39 0 23 ver 49 0 26 ver 8 Sub Clus 2. 2 0 27 ver 44 1 30 ver 11 0 43 t 24 0 43 t 2 SC 1 f 1=vir 19 Rn>4 1 44 t 4 0 52 b 2 SC 1 g 4=b 4 Rn>4 1 0 b 4 0 21 vir 15 SC 1 g 1=b 2 Rn>4 1 0 t 4 0 28 ver 36 Sub. C 1 us 1 has 91, only versicolor and virginica. |ver 49 ver 8 ver 44 ver 11 0. 0 3. 9 7. 1 3. 9 0. 0 1. 4 4. 7 3. 9 1. 4 0. 0 3. 7 7. 1 4. 7 3. 7 0. 0 Almost outliers! Subcluster 2. 2 Which type? Must classify. Sb. Cl_2. 1 g 1=ver 39 Rn>4 1 0 vir 39 0 7 set 21 Note: what remains in Sub. Clus 2. 1 is exactly the 50 setosa. But we wouldn't know that, so we continue to look for outliers and subclusters. Sb. Cl_2. 1 g 1=set 19 Rn>4 none Sb. Cl_2. 1 f 3=set 16 Rn>4 none Sb. Cl_2. 1 Ln. G>4 none Sb. Cl_2. 1 g 3=set 9 Rn>4 none Sb. Cl_2. 1 f 2=set 42 Rn>4 Sb. Cl_2. 1 Ln. G>4 none 1 0 set 42 0 6 set 9 Sb. Cl_2. 1 f 4=set Rn>4 none Sb. Cl_2. 1 f 2=set 9 Rn>4 none Sb. Cl_2. 1 g 4=set Rn>4 none Sb. Cl_2. 1 g 2=set 16 Rn>4 none Sb. Cl_2. 1 Ln. G>4 none fitting"), then we have to conclude that Mark's round gap analysis is more productive than linear dot product proj gap analysis! FFG (Furthest to Furthest), computes Sp. S((M-x)o(M-x)) for f 1 (expensive? Grab any pt? , corner pt? ) then compute Sp. S((x-f 1)o(x-f 1)) for f 1 -round-gapanalysis. Then compute Sp. S(xod 1) to get g 1 to have projection furthest from that of f 1 ( for d 1 linear gap analysis) (Too expensive? since gk-round-gap-analysis and linear analysis contributed very little! But we need it to get f 2, etc. Are there other cheaper ways to get a good f 2? Need Sp. S((x-g 1)o(x-g 1)) for g 1 round-gap-analysis (too expensive!)
Mark 10/15 (“thin” gap using tfxidf). Classification left, reuters text right. Seems right on! Mining and assays grouped, anomalies are gold strikes (vs. production), livestock. Min gap needs to be from the MSB not LSB - ie, how many bits to consider for gaps. Reason: as you add attributes, the distances start getting large, so needs to be relative. I seem to get better results with oblique rather than round, but jury still out…. JAPAN'S DOWA MINING TO PRODUCE GOLD FROM APRIL TOKYO, 3/16 - Dowa Mining Co Ltd> said it will start commercial production of gold, copper, lead 0 and zinc from its Nurukawa Mine in northern Japan in April. A company spokesman said the mine's monthly output is expected to consist of 1, 300 tonnes of gold ore and 3, 700 of black ore, which consists of copper, lead and zinc ores. A company survey shows the gold ore contains up to 13. 3 grams of gold per tonne, he said. Proven gold ore reserves amount to 50, 000 tonnes while estimated reserves of gold and black ores total one mln tonnes, he added. GERMAN BANK SEES HIGHER GOLD PRICE FOR 1987 HAMBURG, March 16 - Gold is expected to continue its rise this year due to renewed inflationary pressures, especially in the U. S. , Hamburg-based Vereins- und Westbank AG said. It said in a statement the stabilisation of crude oil prices and the Organisation of 0 Petroleum Exporting Countries' efforts to achieve further firming of the price led to growing inflationary pressures in the U. S. , The world's biggest crude oil producer. Money supplies in the U. S. , Japan and West Germany exceed the central banks' limits and real growth of their gross national products, it said. Use of physical gold should rise this year due to increased industrial demand higher expected coin production, the banksaid. Speculative demand, which influences the gold price on futures markets, has also risen. These factors and South Africa's unstable political situation, which may lead to a temporary reduction in gold supplies from that country, underline the firmer sentiment, it said. However, Australia's output is estimated to rise to 90 tonnes this year from 73. 5 tonnes in 1986. SOME 7, 000 MINERS GO ON STRIKE IN SOUTH AFRICA, 3/16 - Some 7, 000 black miners went on strike at South African gold and coal mines, the National Union of 2 Mineworkers (NUM) said. A NUM spokesman said 6, 000 workers began an underground sit-in at the Grootvlei gold mine, owned by General Union Mining Corp, to protest the transfer of colleagues to different jobs. He said about 1, 000 employees of Anglo American Corp's New Vaal Colliery also downed tools but the reason for the stoppage was not immediately clear. Officials of the two companies were not available for comment and the NUM said it was trying to start negotiations with management. LEVON RESOURCES < LVNVF> GOLD ASSAYS IMPROVED VANCOUVER, British Columbia, March 16 - Levon Resources Ltd said re-checked gold assays from the Howard tunnel on its Congress, British Columbia property yielded higher gold grades than those reported in January and February. It said assays from zone 0 averaged 0. 809 ounces of gold a ton over a 40 foot section with an average width of 6. 26 feet. Levon previously reported the zone averaged 0. 226 ounces of gold a ton over a 40 foot section with average width of 5. 16 feet. Levon said re-checked assays from zone two averaged 0. 693 ounces of gold a ton over a 123 foot section with average width of 4. 66 feet. Levon Resources said the revised zone two assays compared to previously reported averages of 0. 545 ounces of gold a ton over a 103 foot section with average width of 4. 302 feet. Company also said it intersected another vein 90 feet west of zone two, which assayed 0. 531 ounces of gold a ton across a width of 3. 87 feet. BP < BP> UNIT SEES MINE PROCEEDING NEW YORK, March 16 - British Petroleum Co PLC said based on a feasibility report from & lt; Ridgeway Mining Co, its joint venture Ridgeway Project in South Carolina could start commercial gold production by mid-1988. The company said the mine would produce at an approximate rate of 158, 000 ounces of gold per year over the first four full years of operation from 1989 through 1992 and at an average of 133, 000 ounces a year over the full projected 110 year life of the mine. BP's partner in the venture is Galactic Resources of Toronto. The company said subject to receipt of all statutory permits, finalization of financing arrangements and management and joint venture review, construction of a 15, 000 short ton per day processing facility can start. Capital costs to bring the mine into production are estimated at 76 mln dlrs. BP UNIT SEES U. S. GOLD MINE PROCEEDING NEW YORK, March 16 - British Petroleum Co PLC said based on a feasibility report from Ridgeway Mining Co, its joint venture Ridgeway Project in South Carolina could start commercial gold production by mid-1988. The company said the mine would produce approximately 158, 000 0 ounces of gold per year over the first four full years of operation from 1989 through 1992 and at an average 133, 000 ounces a year over the full projected 11 year life of the mine. BP's partner is Galactic Resources Ltd of Toronto. BP said subject to receipt of all statutory permits, finalization of financing arrangements and management and joint venture review, construction of a 15, 000 short ton per day processing facility can start. Capital costs to bring the mine into production are estimated at 76 mln dlrs 0 0 0 1 LEVON RESOURCES REPORTS IMPROVED GOLD ASSAYS VANCOUVER, British Columbia, March 16 - Levon Resources Ltd said re-checked gold assays from the Howard tunnel on its Congress, British Columbia property yielded higher gold grades than those reported in January and February. It said assays from zone averaged 0. 809 ounces of gold a ton. Levon previously reported the zone averaged 0. 226 ounces of gold a ton. Levon said re-checked assays from zone two averaged 0. 693 ounces of gold a ton. Levon Resources said the revised zone two assays compared to previously reported averages of 0. 545 ounces of gold a ton. The company also said it intersected another vein 90 feet west of zone two, which assayed 0. 531 ounces of gold a ton. VICEROY RESOURCE CORP> DETAILS GOLD ASSAYS Vancouver, British Columbia, March 17 - Viceroy Resource Corp said recent drilling on the Lesley Ann deposit extended the high-grade mineralization over a width of 600 feet. Assays ranged from 0. 35 ounces of gold per ton over a 150 -foot interval at a depth of 350 to 500 feet to 1. 1 ounces of gold per ton over a 65 -foot interval at a depth of 200 to 410 feet. STARREX LINKS SHARE PRICE TO ASSAY SPECULATION TORONTO, March 16 - Starrex Mining Corp Ltd> said a sharp rise in its share price is based on speculation for favorable results from its current underground diamond drilling program at its 35 pct owned Star Lake gold mine in northern Saskatchewan. Starrex Mining shares rose 40 cts to 4. 75 dlrs in trading on the Toronto Stock Exchange. The company said drilling results from the program which started in late February are encouraging, "but it is too soon for conclusions. " Starrex did not disclose check assay results from the exploration program. U. S. MEAT GROUP TO FILE TRADE COMPLAINTS WASHINGTON, March 13 -
For speed of text mining (and of other high dimension datamining), we might do additional dimension reduction (after stemming content word). A simple way is to use STD of the column of numbers generated by the functional (e. g. , Xk, Sp. S((x-M)o(x-M)), Sp. S((x-f)o(x-f)), Sp. S(xod), etc. ). The STDs of the columns, Xk, can be precomputed up front, once and for all. STDs of projection and square distance functionals must be done after they are generated (could be done upon capture too). Good functionals produce many large gaps. In Iris 150 and Iris 150+Out 30, I find that the precomputed STD is a good indicator of that. A text mining scheme might be: 1. Capture the text as a PTree. SET (after stemming the content words) and store mean, median, STD of every column (content word stem). 2. Throw out low STD columns. 4'. Use a weighted sum of "importance" and STD? (If the STD is low, there can't be many large gaps. ) A possible Attribute Selection algorithm: 1. Peel from X, outliers using CRM-lin, CRC-lin, possibly M-rnd, fg-rnd. . (Xin = X - Xout) 2. Calculate widths of each Xin-Circumscribing Rectangle edge, crewk 4. Look for wide gaps top down (or, very simply, order by STD). 4'. Divide crewk into count{xk| x Xin}. (but that doesn't account for dups) 4''. look for preponderance of wide thin-gaps top down. 4'''. look for high projection interval count dispersion (STD). Notes: 1. Maybe an inlier sub-cluster needs occur from more than one functional projection to be declared an inlier sub-cluster? 2. STD of a functional projection appears to be a good indicator of the quality of its gap analysis. For FAUST Cluster-d (pick d, then f=Mn. Pt(xod) and g=Mx. Pt(xod) ) a full grid of unit vectors (all directions, equally spaced) may be needed. Such a grid could be constructed using angles a 1, . . . , am, each equi-width partitioned on [0, 180), with the formulas: d = e 1 k=n. . . 2 cos k + e 2 sin 2 k=n. . . 3 cos k + e 3 sin 3 k=n. . . 4 cos k +. . . + ensin n where i's start at 0 and increment by . So, di 1. . in= j=1. . n[ ej sin((ij-1) ) * k=n. . j+1 cos(k ) ]; i 0≡ 0, divides 180 (e. g. , 90, 45, 22. 5. . . ) CRMSTD(dfg) Eliminate all columns with STD < threshold. d 3 Sub 0 10 set 23. . . 50 set+vir 39 Clus 1 1 19 set 25 Sub 0 30 ver 49. . . 50 ver_49 vir Clus 2 0 69 vir 19 d 5 (f 5=vir 23, g 5=set 14) none, f 5 none, g 5 none d 5 (f 5=vir 32, g 5=set 14) none, f 5 none, g 5 none d 5 (f 5=vir 6, g 5=set 14) none, f 5 none, g 5 none (d 1+d 3)/sqr(2) clus 1 none (d 1+d 3)/sqr(2) clus 2: ver 49 ver 8 ver 44 ver 11 0 57. 3 ver 49 0. 0 3. 9 7. 2 0 58. 0 ver 8 3. 9 0. 0 1. 4 4. 6 0 58. 7 ver 44 3. 9 1. 4 0. 0 3. 6 1 60. 1 ver 11 7. 2 4. 6 3. 6 0. 0 0 64. 3 ver 10 none (d 3+d 4)/sqr(2) clus 1 none (d 3+d 4)/sqr(2) clus 2 none (d 1+d 3+d 4)/sqr(3) clus 1 1 44. 5 set 19 0 55. 4 vir 39 (d 1+d 3+d 4)/sqr(3) clus 2 none (d 1+d 2+d 3+d 4)/sqr(4) clus 1 (d 1+d 2+d 3+d 4)/sqr(4) clus 2 none d 5 (f 5=vir 19, g 5=set 14) none f 5 1 0. 0 vir 19 clus 2 0 4. 1 vir 23 g 5 none Just about all the high STD columns find the subcluster split. d 5 (f 5=vir 18, g 5=set 14) none f 5 1 0. 0 vir 18 clus 2 1 4. 1 vir 32 0 8. 2 vir 6 g 5 none In addition, they find the four outliers as well
CRMSTD(dfg) using IRIS rectangle on Satlog (1805 rows of R, G, IR 1, IR 2 with classes {1, 2, 3, 4, 5, 7}. ). Here I made a mistake and left Min. Vec, Max. Vec and M as they were for IRIS (so probably far from the Satlog dataset). The results were good? ? ? Suggests random f and g? d 2 STD=23. 7 gp>3 val cl num 3 361 3 84 3 100 3 315 (d 2+d 3)/sqr 2 STD=23. 6 (d 1+d 2)/sqr 2 STD=25. 3 (d 1+d 4)/sqr 2 STD=15. 5 1 121 1 297 0. 0 7. 3 16. 4 10. 1 1 173. 2 3 244 3 361 3 84 3 100 3 315 1 153. 4 3 200 0 59. 4 5 75 0 126 3 361 7. 3 0. 0 10. 7 3. 9 0 183. 8 3 361 0. 0 7. 3 16. 4 10. 1 0 157. 7 3 315 1 60. 1 5 24 0 127 3 84 16. 4 10. 7 0. 0 11. 5 0 181. 7 3 84 7. 3 0. 0 10. 7 3. 9 1 157. 7 3 84 0 64. 3 5 149. . . 0 128 3 100 10. 1 3. 9 11. 5 0. 0 0 184. 6 3 100 16. 4 10. 7 0. 0 11. 5 0 161. 2 3 361 1 142. 1 3 84 0 128 3 315 0 180. 3 3 315 10. 1 3. 9 11. 5 0. 0 0 145. 7 3 361 d 4 STD=20. 3 gp>3 val cl num SQRT(x-f 2)o(x-f 2) STD=26. 7 (d 1+d 3)/sqr 2 STD=16. 8 d 3+d 4)/sqr 2 STD=25. 7 1 29 5 75 (d 2+d 4)/sqr 2 STD=20. 4 val cl num 1 159. 8 3 84 1 39. 5 5 75 0 40. 0 5 75 1 33 5 24 1 41. 6 5 75 0 166. 9 3 361 0 44. 5 5 24. . . 1 41. 0 5 24. . . 0 37 5 73. . . 0 45. 9 5 24. . . 1 142. 5 2 119 1 109. 5 3 45 1 150 2 85 1 168. 8 3 244 3 361 3 84 3 100 3 315 0 146. 5 2 191 0 115. 0 3 361 0 154 2 191 0 180. 4 3 361 0. 0 7. 3 16. 4 10. 1 0 147. 5 2 85 0 115. 5 3 315 0 178. 1 3 84 7. 3 0. 0 10. 7 3. 9 d 3 STD=17. 2 gp>3 0 116. 0 3 84 0 179. 2 3 100 16. 4 10. 7 0. 0 11. 5 val cl num d 1+d 2+d 3+d 4)/sqr 4 STD=25. 9 0 117. 5 3 100 same 0 176. 1 3 315 10. 1 3. 9 11. 5 0. 0 1 139 2 191 0 92. 5 5 75 d 1+d 2+d 3)/sqr 3 STD=25. 3 0 145 2 85 SQRT(x-g 2)o(x-g 2) STD=26. 8 1 95. 0 5 24 1 203. 8 3 84 val cl num 0 99. 0 5 149 d 1 STD=13. 6 g>3 none 0 209. 0 3 361 1 101. 5 5 73 1 15. 6 5 75 5 149 5 24 5 73 5 168 SQRT(x-M)o(x-M) STD=28 0 105. 0 5 121. . . 0 22. 5 5 149 0. 0 7. 7 4. 6 8. 1 (d 1+d 2+d 4)/sqr 3 STD=21. 9 val cl num 1 222. 0 3 244 0 22. 9 5 24 7. 7 0. 0 7. 1 14. 0 0 67. 0 5 24 0 226. 5 3 315 1 29. 6 5 75 0 24. 1 5 73 4. 6 7. 1 0. 0 7. 3 1 67. 5 5 75 0 227. 0 3 100 1 34. 2 5 24 1 26. 6 5 168 8. 1 14. 0 7. 3 0. 0 0 72. 5 5 149 1 229. 0 3 84 0 38. 7 5 149 0 29. 6 5 121. . . d 1+d 3+d 4/sq 3 STD=22. 1 sqr(x-f 4)o(x-f 4 STD=27. 8 0 233. 0 3 361 same 1 39. 7 5 73 1 162. 1 2 119 val cl num 0 81. 4 5 24 0 43. 7 5 168 0 168. 7 2 191 1 35. 6 5 75 1 77. 4 5 75 SQRT(x-f 1)o(x-f 1) STD=27 0 169. 7 2 85 1 39. 9 5 24 SQRT(x-f 5)o(x-f 5) STD=25 val cl num 0 45. 3 5 149 Skip STD<25, same outliers: val cl num 0 41. 1 5 24 1 45. 7 5 73 SQRT(x-f 3)o(x-f 3) STD=27. 5 2_85, 2_191, 1 147. 1 3 100 1 41. 6 5 75 val cl num 0 50. 8 5 168. . . 3_361, 3_84, 3_100, 3_315, 0 151. 7 2 85 0 44. 9 5 149. . . 1 52. 2 5 75 1 176. 2 2 119 5_24, 5_73, 5_75, 5_149, 5_168, 0 152. 3 2 191 1 172. 8 3 84 0 58. 0 5 24 0 182. 9 2 191 0 176. 6 3 361 SQRT(x-g 4)o(x-g 4) STD=27. 7 1 58. 2 5 149 0 182. 9 2 85 SQRTx-g 5 ox-g 5 STD=27. 4 val cl num 0 61. 5 5 73 SQRT(x-g 1)o(x-g 1) STD=26. 3 val cl num 1 144. 8 2 119 3 315 2 191 3 84 3 100 2 85 3 361 1 62. 5 5 168 val cl num 0 27. 8 5 75 0 148. 6 3 315 0. 0 120. 7 3. 9 11. 5 122. 2 10. 1 0 66. 0 5 121. . . 1 41. 6 5 75 1 29. 4 5 24 0 150. 7 2 191 120. 7 0. 0 119. 2 115. 0 7. 8 121. 3 1 188. 2 3 361 0 45. 9 5 24. . . 0 150. 9 3 84 3. 9 119. 2 0. 0 10. 7 120. 7 7. 3 0 35. 1 5 73 0 192. 0 2 191 0 151. 8 3 100 11. 5 115. 0 10. 7 0. 0 116. 4 1 166. 1 2 119 1 35. 6 5 149 0 193. 6 2 85 0 151. 8 2 85 122. 2 7. 8 120. 7 116. 4 0. 0 122. 5 0 172. 3 2 191 0 39. 4 5 71 SQRT(x-g 3)o(x-g 3) STD=24. 9 none 0 153. 9 3 361 10. 1 121. 3 7. 3 16. 4 122. 5 0. 0 0 172. 8 2 85
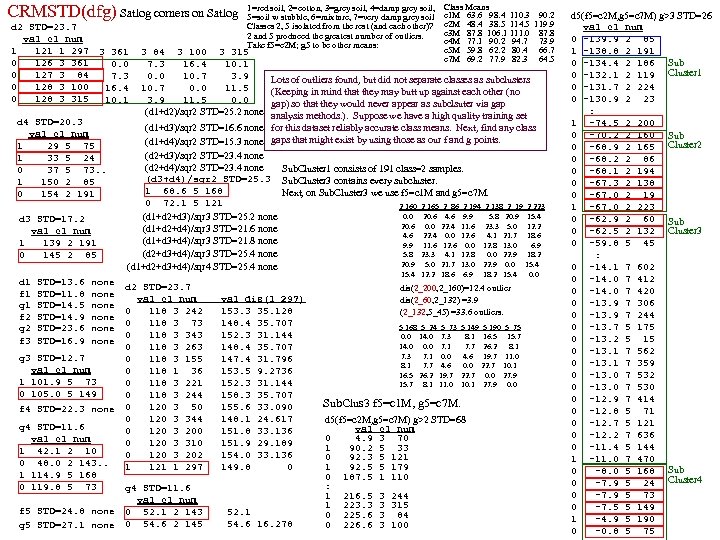CRMSTD(dfg) Satlog corners on Satlog d 2 STD=23. 7 val cl num 1 121 1 297 0 126 3 361 0 127 3 84 0 128 3 100 0 128 3 315 1=red soil, 2=cotton, 3=grey soil, 4=damp grey soil, 5=soil w stubble, 6=mixture, 7=very damp grey soil Classes 2, 5 isolated from the rest (and each other)? 2 and 5 produced the greatest number of outliers. Take f 5=c 2 M; g 5 to be other means: 3 361 3 84 3 100 3 315 0. 0 7. 3 16. 4 10. 1 7. 3 0. 0 10. 7 3. 9 16. 4 10. 7 0. 0 11. 5 10. 1 3. 9 11. 5 0. 0 (d 1+d 2)/sqr 2 STD=25. 2 none d 4 STD=20. 3 val cl num 1 29 5 75 1 33 5 24 0 37 5 73. . 1 150 2 85 0 154 2 191 d 3 STD=17. 2 val cl num 1 139 2 191 0 145 2 85 d 1 STD=13. 6 none f 1 STD=11. 8 none g 1 STD=14. 5 none f 2 STD=14. 9 none g 2 STD=23. 6 none f 3 STD=16. 9 none g 3 STD=12. 7 val cl num 1 101. 9 5 73 0 105. 0 5 149 f 4 STD=22. 3 none g 4 STD=11. 6 val cl num 1 42. 1 2 10 0 48. 0 2 143. . 1 114. 9 5 168 0 119. 8 5 73 f 5 STD=24. 8 none g 5 STD=27. 1 none Class Means c 1 M 63. 6 98. 4 110. 3 90. 2 c 2 M 48. 4 38. 5 114. 5 119. 9 c 3 M 87. 8 106. 1 111. 0 87. 8 c 4 M 77. 1 90. 2 94. 7 73. 9 c 5 M 59. 8 62. 2 80. 4 66. 7 c 7 M 69. 2 77. 9 82. 3 64. 5 Lots of outliers found, but did not separate classes as subclusters (Keeping in mind that they may butt up against each other (no gap) so that they would never appear as subclsuter via gap analysis methods. ). Suppose we have a high quality training set (d 1+d 3)/sqr 2 STD=16. 6 none for this dataset reliably accurate class means. Next, find any class (d 1+d 4)/sqr 2 STD=15. 3 none gaps that might exist by using those as our f and g points. (d 2+d 3)/sqr 2 STD=23. 4 none (d 2+d 4)/sqr 2 STD=23. 4 none Sub. Cluster 1 consists of 191 class=2 samples. (d 3+d 4)/sqr 2 STD=25. 3 Sub. Cluster 3 contains every subcluster. 1 68. 6 5 168 Next, on Sub. Cluster 3 we use f 5=c 1 M and g 5=c 7 M. 0 72. 1 5 121 2 160 2 165 2 86 2 194 2 138 2 19 2 223 0. 0 20. 6 4. 6 9. 9 5. 8 20. 9 15. 4 (d 1+d 2+d 3)/sqr 3 STD=25. 2 none 20. 6 0. 0 22. 4 11. 6 23. 3 5. 0 12. 2 (d 1+d 2+d 4)/sqr 3 STD=21. 6 none 4. 6 22. 4 0. 0 12. 6 4. 1 21. 7 18. 6 (d 1+d 3+d 4)/sqr 3 STD=21. 8 none 9. 9 11. 6 12. 6 0. 0 12. 8 13. 0 6. 9 (d 2+d 3+d 4)/sqr 3 STD=25. 4 none 5. 8 23. 3 4. 1 12. 8 0. 0 22. 9 18. 2 20. 9 5. 0 21. 7 13. 0 22. 9 0. 0 15. 4 (d 1+d 2+d 3+d 4)/sqr 4 STD=25. 4 none 15. 4 12. 2 18. 6 6. 9 18. 2 15. 4 0. 0 d 2 STD=23. 7 val cl num val dis(1 297) 0 118 3 242 153. 3 35. 128 0 118 3 73 148. 4 35. 707 0 118 3 343 152. 3 31. 144 0 118 3 263 148. 4 35. 707 0 118 3 155 147. 4 31. 796 0 118 1 36 153. 5 9. 2736 0 118 3 221 152. 3 31. 144 0 118 3 244 158. 3 35. 707 0 120 3 50 155. 6 33. 090 0 120 3 344 148. 1 24. 617 0 120 3 200 151. 8 33. 136 0 120 3 310 151. 9 29. 189 0 120 3 202 154. 0 33. 136 1 121 1 297 149. 8 0 g 4 STD=11. 6 val cl num 0 52. 1 2 143 52. 1 0 54. 6 2 145 54. 6 16. 278 dis(2_200, 2_160)=12. 4 outlier dis(2_60, 2_132) =3. 9 2_132, 5_45) =33. 6 outliers. ( 5 168 5 24 5 73 5 149 5 190 5 75 0. 0 14. 0 7. 3 8. 1 16. 5 15. 7 14. 0 0. 0 7. 1 7. 7 26. 2 8. 1 7. 3 7. 1 0. 0 4. 6 19. 7 11. 0 8. 1 7. 7 4. 6 0. 0 22. 7 10. 1 16. 5 26. 2 19. 7 22. 7 0. 0 27. 9 15. 7 8. 1 11. 0 10. 1 27. 9 0. 0 Sub. Clus 3 f 5=c 1 M, g 5=c 7 M. d 5(f 5=c 2 M, g 5=c 7 M) g>2 STD=68 val cl num 0 4. 9 3 70 1 90. 2 5 33 0 92. 3 5 121 1 92. 5 5 179 0 187. 5 1 110 : 1 216. 5 3 244 1 223. 3 3 315 0 225. 6 3 84 0 226. 6 3 100 d 5(f 5=c 2 M, g 5=c 7 M) g>3 STD=26 val cl num 0 -139. 9 2 85 1 -138. 8 2 191 0 -134. 4 2 186 Sub 0 -132. 1 2 119 Cluster 1 0 -131. 7 2 224 0 -130. 9 2 23 : 1 -74. 5 2 200 0 -70. 2 2 160 Sub 0 -68. 9 2 165 Cluster 2 0 -68. 2 2 86 0 -68. 1 2 194 0 -67. 3 2 138 0 -67. 0 2 19 1 -67. 0 2 223 0 -62. 9 2 60 Sub 0 -62. 5 2 132 Cluster 3 0 -59. 8 5 45 : 0 -14. 1 7 602 0 -14. 0 7 412 0 -14. 0 7 420 0 -13. 9 7 306 0 -13. 9 7 244 0 -13. 7 5 175 0 -13. 2 5 15 0 -13. 1 7 562 0 -13. 1 7 359 0 -13. 0 7 532 0 -13. 0 7 530 0 -12. 9 7 414 0 -12. 8 5 71 0 -12. 7 5 121 0 -12. 2 7 636 0 -11. 4 5 144 1 -11. 0 7 470 0 -8. 0 5 168 Sub 0 -7. 9 5 24 Cluster 4 0 -7. 9 5 73 0 -7. 5 5 149 1 -4. 9 5 190 0 -0. 8 5 75
Density: A set is T-dense iff it has no distance gaps greater than T. 10/20/12 (Equivalently, every point has neighbors in its' T-neighborhood. ) We can use L 1 or HOB or L distance, since dis. L (x, y); dis. L (x, y) 2*dis. HOB(x, y) and dis. L (x, y) n*dis. L (x, y) 1 2 2 2 Definition: Y X is T-dense iff there does not exist y Y such that dis 2(y, Y-{y}) > T. Theorem-1: If for every y Y, dis 2(y, Y-{y}) T then Y is T-dense. Using L 1 distance, not L 2=Euclidean: Theorem-2: dis. L 1(x, y) dis. L 2(x, y) (from here on we will use disk to mean dis. Lk ). Therefore: If, for every y Y, dis 1(y, Y-{y}) T then Y is T-dense. ( Proof: dis 2(y, Y-{y}) dis 1(y, Y-{y}) T ) 2*dis. HOB(x, y) dis 2(x, y) (Proof: Let the bit pattern of dis 2(x, y) be 001 bk-1. . . b 0 then dis. HOB(x, y)=2 k and the most bk-1. . . b 0 can contribute is 2 k-1 (if it's all 1 -bits). So dis 2(x, y) 2 k + (2 k - 1) 2*2 k = 2*dis. HOB(x, y). Theorem-3: If, for every y Y, dis. HOB(y, Y-{y}) T/2 then Y is T-dense. Proof: dis 2(y, Y-{y}) 2*dis. HOB(y, Y-{y}) 2*T/2 = T Theorem-4: If, for every y Y, dis (y, Y-{y}) T/n then Y is T-dense. Proof: dis 2(y, Y-{y}) n*dis. HOB(y, Y-{y}) n*T/n = T Pick T' based on T and the dimension, n (It can be done!). If Max. Gap(yoek)=Max. Gap(Yk) < T' k=1. . n, then Y is T-dense (Recall, yoek is just Yk as a column of values. ) Note: We use the logn p. Tree. Gap. Finder to avoid sorting. Unfortunately, it doesn't immediately find all gaps precisely at their full width (because it descends using power of 2 widths), but if we find all PTree. Gaps, we can be assured that Max. PTree. Gap(Y) Max. Gap(Y) or we can keep track of "thin gaps" and thereby actually identify all gaps (see the slide on p. Tree. Gap. Finder). Theorem-5: If k=1. . n. Max. Gap(Yk) T, then Y is T-dense Proof: dis 1(y, x)≡ k=1. . n|yk-xk|. |yk-xk| Max. Gap(Yk) x Y. So dis 2(y, Y-{y}) dis 1(y, Y-{y}) k=1. . n. Max. Gap(Yk) T
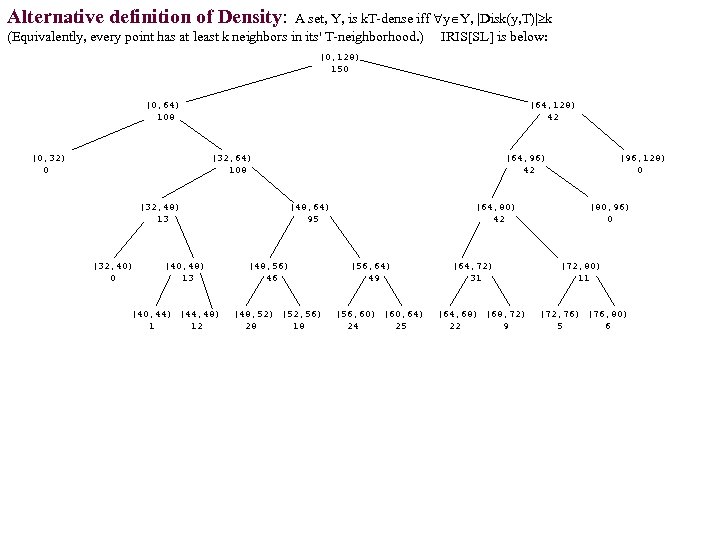Alternative definition of Density: A set, Y, is k. T-dense iff y Y, |Disk(y, T)| k (Equivalently, every point has at least k neighbors in its' T-neighborhood. ) IRIS[SL] is below: [0, 128) 150 [0, 64) [64, 128) 108 42 [0, 32) [32, 64) [64, 96) [96, 128) 0 108 42 0 [32, 48) [48, 64) [64, 80) [80, 96) 13 95 42 0 [32, 40) [40, 48) [48, 56) [56, 64) [64, 72) [72, 80) 0 13 46 49 31 11 [40, 44) [44, 48) [48, 52) [52, 56) [56, 60) [60, 64) [64, 68) [68, 72) [72, 76) [76, 80) 1 12 28 18 24 25 22 9 5 6
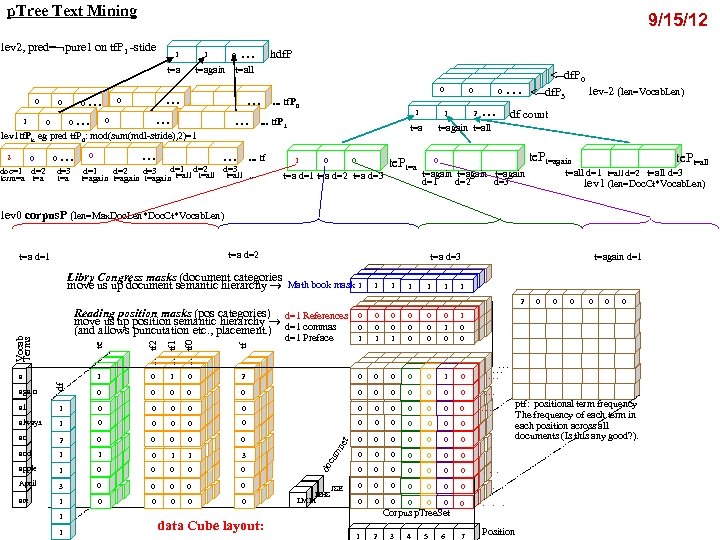p. Tree Text Mining 9/15/12 lev 2, pred= pure 1 on tf. P 1 -stide 1 hdf. P 0 . . . 1 t=again t=all 0 1 0 0 . . . 0 . . . tf. P 0 . . . tf. P 1 lev 1 tf. Pk eg pred tf. P 0: mod(sum(mdl-stride), 2)=1 2 0 0 . . . doc=1 d=2 d=3 term=a t=a . . . 0 . . . tf d=1 d=2 d=3 t=all . . . t=again 1 8 8 0 1 1 1 3 3 3 0 . . . 2 . . . t=again t=all 1 . . . 8 0 1 te. Pt=a 0 0 <--df. P 0 lev-2 (len=Vocab. Len) <--df. P 3 df count te. Pt=again d=1 d=2 d=3 t=a d=1 t=a d=2 t=a d=3 lev 0 corpus. P (len=Max. Doc. Len*Doc. Ct*Vocab. Len) t=a d=2 t=a d=1 t=a d=3 Libry Congress masks (document categories move us up document semantic hierarchy Math book mask 1 1 1 1 0 0 0 0 0 1 0 t=again d=1 1 0 0 2 . . . tf 0 1 0 2 0 0 0 0 0 1 0 0 0 0 0 . . . always. 1 0 0 0 an 2 0 0 0 and 1 1 0 1 1 3 0 0 0 0 apple 0 0 0 0 . . . 0 0 0 0 . 0 0 0 3 0 0 0 are 1 0 0 0 1 data Cube layout: mn cu do 1 April et all 1 0 0 0 . . . 0 again 0 . . . 0 . . . df . . . tf 1 1 a . . . tf 2 d=1 Preface te Vocab Terms Reading position masks (pos categories) d=1 References move us up position semantic hierarchy d=1 commas (and allows puncutation etc. , placement. ) JSE HHS LMM Corpus p. Tree. Set 1 2 3 4 5 6 7 Position te. Pt=all d=1 t=all d=2 t=all d=3 lev 1 (len=Doc. Ct*Vocab. Len) ptf: positional term frequency The frequency of each term in each position across all documents (Is this any good? ).
tf a b f l b r b c c c c i g w a b b b r i r c h l l c r d f g r h h a w a a b b e g o b a i e o o o c c d i d e a d u i e i i y a b c a a k e o a h w u k l a t c w r u a s o a l l l r e g l s y y k d g e d y d t n y e d n h k n y t y h g t l e l l n h l h m m o r t t w o k l l m e o m t n p o s h h t t w o w u i a a a m r n o h o o p p l u r i s r u o r t w i m o s n d m i e r e s l i i u n o e m w e w a f a o e g y b d n y y n r e d e g m d n g n e b n e o y e n l 01 TBM 0 0 0 0 0 1 0 0 02 TLP 0 0 0 0 0 0 0 0 03 DDD 0 0 0 0 1 0 0 0 0 0 0 04 LMM 0 1 0 0 0 0 0 0 1 0 0 0 05 HDS 0 0 0 0 0 0 0 1 0 0 0 06 SPP 0 0 1 0 0 0 0 2 0 0 07 OMH 0 0 0 1 0 0 0 0 0 3 0 0 0 0 08 JSC 0 0 0 0 1 0 0 0 0 2 0 0 0 09 HBD 0 0 1 0 0 0 0 0 0 0 0 10 JAJ 0 0 0 0 0 0 1 0 0 0 1 11 OMM 0 0 0 0 0 0 0 0 12 OWF 0 0 0 0 1 0 0 0 0 0 13 RRS 0 0 0 1 0 0 0 0 0 0 14 ASO 0 0 0 0 0 1 0 0 0 15 PCD 0 0 0 0 0 0 1 0 0 0 0 1 0 16 PPG 0 0 0 1 0 0 0 0 0 0 0 17 FEC 0 0 0 0 0 1 0 0 0 0 18 HTP 0 0 0 0 0 1 0 0 0 0 0 21 LAU 0 0 0 0 0 1 0 1 0 0 0 0 22 HLH 0 0 0 0 0 0 0 0 23 MTB 0 0 0 1 0 0 0 0 0 0 0 25 WOW 0 0 0 0 0 0 0 0 26 SBS 1 0 4 0 0 0 1 1 0 0 0 0 1 0 0 27 CBC 0 0 1 0 0 0 0 2 0 0 0 28 BBB 0 0 0 1 0 0 0 0 1 0 0 29 LFW 1 1 0 0 0 0 0 0 0 0 30 HDD 0 1 0 0 0 0 0 1 1 0 0 0 0 0 32 JGF 0 0 0 0 0 0 1 0 0 4 0 0 0 33 BFP 0 0 0 2 0 0 0 0 1 0 0 0 35 SSS 0 0 0 1 0 0 0 1 0 1 0 0 0 0 36 LTT 0 0 0 0 0 0 0 0 37 MBB 0 0 0 0 4 0 0 0 0 38 YLS 0 0 0 0 0 2 0 0 0 39 LCS 0 1 0 0 0 0 3 0 0 0 1 0 0 41 OKC 0 0 0 0 0 0 0 5 0 0 0 42 BBC 0 0 0 1 0 0 0 0 0 43 HHD 0 0 0 0 0 0 1 0 0 0 0 44 HLH 0 0 0 0 0 1 0 0 0 0 0 1 1 45 BBB 0 0 2 0 0 0 0 0 1 0 0 0 0 0 46 TTP 0 1 0 0 0 0 0 1 0 0 0 0 0 47 CCM 0 0 0 0 1 0 0 0 0 48 OTB 0 0 0 0 0 0 0 0 49 WLG 0 0 1 0 0 0 0 0 0 1 0 0 0 50 LJH 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 2 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 2 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 2 0 0 1 0 2 0 0 0 0 1 0 0 0 0 0 0 0 0 0 5 0 0 0 2 0 0 0 0 8 0 0 0 4 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 2 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 3 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 60 content words from 44 Mother Goose documents (listed on the next slide). I started with 50 documents, but only documents with at least two content words were kept.
01 TBM 02 TLP 03 DDD 04 LMM 05 HDS 06 SPP 07 OMH 08 JSC 09 HBD 10 JAJ 11 OMM 12 OWF 13 RRS 14 ASO 15 PCD 16 PPG 17 FEC 18 HTP 21 LAU 22 HLH 23 MTB 25 WOW 26 SBS 27 CBC 28 BBB 29 LFW 30 HDD 32 JGF 33 BFP 35 SSS 36 LTT 37 MBB 38 YLS 39 LCS 41 OKC 42 BBC 43 HHD 44 HLH 45 BBB 46 TTP 47 CCM 48 OTB 49 WLG Three blind mice! See how they run! They all ran after the farmer's wife, who cut off their tails with a carving knife. Did you ever see such a thing in your life as three blind mice? This little pig went to market. This little pig stayed at home. This little pig had roast beef. This little pig had none. This little pig said Wee, wee. I can't find my way home. Diddle dumpling, my son John. Went to bed with his breeches on, one stocking off, and one stocking on. Diddle dumpling, my son John. Little Miss Muffet sat on a tuffet, eating of curds and whey. There came a big spider and sat down beside her and frightened Miss Muffet away. Humpty Dumpty sat on a wall. Humpty Dumpty had a great fall. All the Kings horses, and all the Kings men cannot put Humpty Dumpty together again. See a pin and pick it up. All the day you will have good luck. See a pin and let it lay. Bad luck you will have all the day. Old Mother Hubbard went to the cupboard to give her poor dog a bone. But when she got there the cupboard was bare and so the poor dog had none. She went to the baker to buy him some bread. When she came back the dog was dead. Jack Sprat could eat no fat. His wife could eat no lean. And so between them both they licked the platter clean. Hush baby. Daddy is near. Mamma is a lady and that is very clear. Jack and Jill went up the hill to fetch a pail of water. Jack fell down, and broke his crown and Jill came tumbling after. When up Jack got and off did trot as fast as he could caper, to old Dame Dob who patched his nob with vinegar and brown paper. One misty morning when cloudy was the weather, I met an old man clothed all in leather. He began to praise and I began to grin. How do you do? And how do you do again? There came an old woman from France who taught grown-up children to dance. But they were so stiff she sent them home in a sniff. This sprightly old woman from France. A robin and a robins son once went to town to buy a bun. They could not decide on plum or plain. And so they went back home again. If all the seas were one sea, what a great sea that would be! And if all the trees were one tree, what a great tree that would be! And if all the axes were one axe, what a great axe that would be! And if all the men were one man, what a great man he would be! And if the great man took the great axe and cut down the great tree and let it fall into the great sea, what a splish splash that would be! Great A. little a. This is pancake day. Toss the ball high. Throw the ball low. Those that come after may sing heigh ho! Flour of England, fruit of Spain, met together in a shower of rain. Put in a bag tied round with a string. If you'll tell me this riddle, I will give you a ring. Here sits the Lord Mayor. Here sit his two men. Here sits the cock. Here sits the hen. Here sit the little chickens. Here they run in. Chin chopper, chin! I had two pigeons bright and gay. They flew from me the other day. What was the reason they did go? I can not tell, for I do not know. The Lion and the Unicorn were fighting for the crown. The Lion beat the Unicorn all around the town. Some gave them white bread and some gave them brown. Some gave them plum cake, and sent them out of town. I had a little husband no bigger than my thumb. I put him in a pint pot, and I bid him drum. I bought a little hanky to wipe his little nose and a pair of little garters to tie his little hose. How many miles to Babylon? Three score miles and ten. Can I get there by candle light? Yes, and back again. If your heels are nimble and light, you may get there by candle light. There was an old woman, and what do you think? She lived on nothing but victuals and drink. Victuals and drink were the chief of her diet, yet this old woman could never be quiet. Sleep baby sleep. Our cottage valley is deep. The little lamb is on the green with woolly fleece so soft and clean. Sleep baby sleep, down where the woodbines creep. Be always like the lamb so mild, a kind and sweet and gentle child. Sleep baby sleep. Cry baby cry. Put your finger in your eye and tell your mother it was not I. Baa black sheep, have you any wool? Yes sir yes sir, three bags full. One for my master and one for my dame, but none for the little boy who cries in the lane. When little Fred went to bed, he always said his prayers. He kissed his mamma and then his papa, and straight away went upstairs. Hey diddle! The cat and the fiddle. The cow jumped over the moon. The little dog laughed to see such sport, and the dish ran away with the spoon. Jack, come and give me your fiddle, if ever you mean to thrive. No I will not give my fiddle to any man alive. If I should give my fiddle, they will think that I have gone mad. For many a joyous day, my fiddle and I have had. Buttons, a farthing a pair! Come, who will buy them of me? They are round and sound and pretty and fit for girls of the city. Come, who will buy them ? Buttons, a farthing a pair! Sing a song of sixpence, a pocket full of rye. Four and twenty blackbirds, baked in a pie. When the pie was opened, the birds began to sing. Was not that a dainty dish to set before the king? The king was in his counting house, counting out his money. The queen was in the parlor, eating bread and honey. The maid was in the garden, hanging out the clothes. When down came a blackbird and snapped off her nose. Little Tommy Tittlemouse lived in a little house. He caught fishes in other mens ditches. Here we go round the mulberry bush, the mulberry bush. Here we go round the mulberry bush, on a cold and frosty morning. This is the way we wash our hands, wash our hands. This is the way we wash our hands, on a cold and frosty morning. This is the way we wash our clothes, wash our clothes. This is the way we wash our clothes, on a cold and frosty morning. This is the way we go to school, go to school. This is the way we go to school, on a cold and frosty morning. This is the way we come out of school, come out of school. This is the way we come out of school, on a cold and frosty morning. If I had as much money as I could tell, I never would cry young lambs to sell. Young lambs to sell, young lambs to sell. I never would cry young lambs to sell. A little cock sparrow sat on a green tree. And he chirped and chirped, so merry was he. A naughty boy with his bow and arrow, determined to shoot this little cock sparrow. This little cock sparrow shall make me a stew, and his giblets shall make me a little pie, too. Oh no, says the sparrow, I will not make a stew. So he flapped his wings and away he flew. Old King Cole was a merry old soul. And a merry old soul was he. He called for his pipe and he called for his bowl and he called for his fiddlers three. And every fiddler, he had a fine fiddle and a very fine fiddle had he. There is none so rare as can compare with King Cole and his fiddlers three. Bat bat, come under my hat and I will give you a slice of bacon. And when I bake I will give you a cake, if I am not mistaken. Hark hark, the dogs do bark! Beggars are coming to town. Some in jags and some in rags and some in velvet gowns. The hart he loves the high wood. The hare she loves the hill. The Knight he loves his bright sword. The Lady loves her will. Bye baby bunting. Father has gone hunting. Mother has gone milking. Sister has gone silking. And brother has gone to buy a skin to wrap the baby bunting in. Tom the piper's son, stole a pig and away he run. The pig was eat and Tom was beat and Tom ran crying down the street. Cocks crow in the morn to tell us to rise and he who lies late will never be wise. For early to bed and early to rise, is the way to be healthy and wise. One two, buckle my shoe. Three four, knock at the door. Five six, ick up sticks. Seven eight, lay them straight. Nine ten. a good fat hen. Eleven twelve, dig and delve. Thirteen fourteen, maids a courting. Fifteen sixteen, maids in the kitchen. Seventeen eighteen. maids a waiting. Nineteen twenty, my plate is empty. There was a little girl who had a little curl right in the middle of her forehead. When she was good she was very good and when she was bad she was horrid.
te a b f l b r b c c c c i g w a b b b r i r c h l l c r d f g r h h a w a a b b e g o b a i e o o o c c d i d e a d u i e i i y a b c a a k e o a h w u k l a t c w r u a s o a l l l r e g l s y y k d g e d y d t n y e d n h k n y t y h g t l e l l n h l h m m o r t t w o k l l m e o m t n p o s h h t t w o w u i a a a m r n o h o o p p l u r i s r u o r t w i m o s n d m i e r e s l i i u n o e m w e w a f a o e g y b d n y y n r e d e g m d n g n e b n e o y e n l 01 TBM 0 0 0 0 0 1 0 0 02 TLP 0 0 0 0 0 0 0 0 03 DDD 0 0 0 0 1 0 0 0 0 0 0 04 LMM 0 1 0 0 0 0 0 0 1 0 0 0 05 HDS 0 0 0 0 0 0 0 1 0 0 0 06 SPP 0 0 1 0 0 0 0 0 07 OMH 0 0 0 1 0 0 0 0 0 1 0 0 0 0 08 JSC 0 0 0 0 1 0 0 0 09 HBD 0 0 1 0 0 0 0 0 0 0 0 10 JAJ 0 0 0 0 0 0 1 0 0 0 1 11 OMM 0 0 0 0 0 0 0 0 12 OWF 0 0 0 0 1 0 0 0 0 0 13 RRS 0 0 0 1 0 0 0 0 0 0 14 ASO 0 0 0 0 0 1 0 0 0 15 PCD 0 0 0 0 0 0 1 0 0 0 0 1 0 16 PPG 0 0 0 1 0 0 0 0 0 0 0 17 FEC 0 0 0 0 0 1 0 0 0 0 18 HTP 0 0 0 0 0 1 0 0 0 0 0 21 LAU 0 0 0 0 0 1 0 1 0 0 0 0 22 HLH 0 0 0 0 0 0 0 0 23 MTB 0 0 0 1 0 0 0 0 0 0 0 25 WOW 0 0 0 0 0 0 0 0 26 SBS 1 0 0 0 1 1 0 0 0 0 1 0 0 27 CBC 0 0 1 0 0 0 0 0 0 28 BBB 0 0 0 1 0 0 0 0 1 0 0 29 LFW 1 1 0 0 0 0 0 0 0 0 30 HDD 0 1 0 0 0 0 0 1 1 0 0 0 0 0 32 JGF 0 0 0 0 0 0 1 0 0 0 0 0 33 BFP 0 0 0 0 0 0 1 0 0 0 35 SSS 0 0 0 1 0 0 0 1 0 1 0 0 0 0 36 LTT 0 0 0 0 0 0 0 0 37 MBB 0 0 0 0 1 0 0 0 0 38 YLS 0 0 0 0 0 1 0 0 0 39 LCS 0 1 0 0 0 0 1 0 0 0 1 0 0 41 OKC 0 0 0 0 0 0 0 1 0 0 0 42 BBC 0 0 0 1 0 0 0 0 0 43 HHD 0 0 0 0 0 0 1 0 0 0 0 44 HLH 0 0 0 0 0 1 0 0 0 0 0 1 1 45 BBB 0 0 1 0 0 0 0 0 0 0 46 TTP 0 1 0 0 0 0 0 1 0 0 0 0 0 47 CCM 0 0 0 0 1 0 0 0 0 48 OTB 0 0 0 0 0 0 0 0 49 WLG 0 0 1 0 0 0 0 0 0 1 0 0 0 50 LJH 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 df 2 5 4 3 2 2 3 3 2 2 4 2 2 2 3 3 2 4 2 3 5 3 3 2 2 2 6 2 2 2 5 2 6 3 2 3 3 4 2 3 5 2 3 2 2 2
mtf=10 a b f *tf/df l b r b c c c c i g w a b b b r i r c h l l c r d f g r h h a w a a b b e g o b a i e o o o c c d i d e a d u i e i i y a b c a a k e o a h w u k l a t c w r u a s o a l l l r e g l s y y k d g e d y d t n y e d n h k n y t y h g t l e l l n h l h m m o r t t w o k l l m e o m t n p o s h h t t w o w u i a a a m r n o h o o p p l u r i s r u o r t w i m o s n d m i e r e s l i i u n o e m w e w a f a o e g y b d n y y n r e d e g m d n g n e b n e o y e n l 01 TBM 0 0 0 0 0 5 0 0 02 TLP 0 0 0 0 0 0 0 0 03 DDD 0 0 0 0 3 0 0 0 0 0 0 04 LMM 0 2 0 0 0 0 0 0 2 0 0 0 05 HDS 0 0 0 0 0 0 0 3 0 0 0 06 SPP 0 0 5 0 0 0 0 0 07 OMH 0 0 0 3 0 0 0 0 0 100 0 0 0 08 JSC 0 0 0 0 5 0 0 0 0 4 0 0 0 09 HBD 0 0 3 0 0 0 0 0 0 0 0 10 JAJ 0 0 0 5 0 0 0 3 0 0 0 5 11 OMM 0 0 0 0 3 0 0 0 0 12 OWF 0 0 0 0 5 0 0 0 0 0 13 RRS 0 0 0 3 0 0 0 0 0 0 14 ASO 0 0 0 0 0 5 0 0 3 0 0 0 15 PCD 0 0 0 0 0 0 3 0 0 0 0 5 0 16 PPG 0 0 0 5 0 0 0 0 0 0 0 17 FEC 0 0 0 0 0 3 0 0 0 0 18 HTP 0 0 0 0 0 5 0 0 0 0 0 3 0 0 0 0 0 21 LAU 0 0 0 0 0 3 0 5 0 0 0 0 22 HLH 0 0 0 0 0 0 0 0 23 MTB 0 0 0 3 0 0 0 0 0 0 0 25 WOW 0 0 0 0 0 0 0 0 26 SBS 5 0 100 0 0 5 5 0 0 0 0 5 0 0 27 CBC 0 0 3 0 0 0 0 5 0 0 0 28 BBB 0 0 0 5 0 0 3 0 0 0 0 5 0 0 29 LFW 5 2 0 0 0 3 0 0 0 0 0 0 30 HDD 0 2 0 0 0 0 0 5 3 0 0 0 0 0 32 JGF 0 0 0 0 0 0 3 0 0 130 0 0 33 BFP 0 0 0 0 0 0 5 0 0 0 35 SSS 0 0 0 3 0 0 0 5 0 2 0 0 5 0 0 36 LTT 0 0 0 0 0 0 0 0 37 MBB 0 0 0 0 100 0 0 0 38 YLS 0 0 0 0 0 5 0 0 0 39 LCS 0 2 0 0 0 3 0 0 0 0 100 0 0 5 0 0 41 OKC 0 0 0 0 0 0 0 170 0 0 42 BBC 0 0 0 3 0 0 0 5 0 0 0 0 0 43 HHD 0 0 0 0 0 0 3 0 0 0 0 44 HLH 0 0 0 0 0 5 0 0 0 0 0 5 5 45 BBB 0 0 5 0 0 0 0 0 3 0 0 0 0 0 46 TTP 0 2 0 0 0 0 0 3 0 0 2 0 0 0 0 47 CCM 0 0 0 0 3 0 0 0 0 48 OTB 0 0 0 0 0 0 0 0 49 WLG 0 0 5 0 0 0 0 0 0 5 0 0 0 50 LJH 0 0 0 0 3 0 0 0 0 2 0 0 0 0 0 0 3 0 0 4 0 0 0 0 0 5 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 7 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 3 0 0 0 0 100 0 0 0 3 0 0 0 0 0 0 7 0 0 0 0 200 0 0 0 0 0 5 0 0 0 0 0 0 0 3 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 5 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 7 0 0 0 0 5 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 3 0 0 0 0 100 0 0 0 0 0 0 5 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 5 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 3 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 3 0 0 0 5 7 0 0 5 0 7 0 0 100 0 0 0 0 5 0 0 2 0 0 0 0 0 0 0 0 250 0 0 7 0 0 0 0 270 0 0 200 0 0 5 0 0 0 0 0 0 0 5 0 0 0 3 0 0 0 0 0 5 0 0 0 7 0 0 100 0 3 0 0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 5 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 100 0 3 0 0 0 0 0 5 0 0 0 0 3 0 0 0 0 150 0 0 0 2 0 0 0 5 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 5 0 0 0 0
mtf 0 a b f l b r b c c c c i g w a b b b r i r c h l l c r d f g r h h a w a a b b e g o b a i e o o o c c d i d e a d u i e i i y a b c a a k e o a h w u k l a t c w r u a s o a l l l r e g l s y y k d g e d y d t n y e d n h k n y t y h g t l e l l n h l h m m o r t t w o k l l m e o m t n p o s h h t t w o w u i a a a m r n o h o o p p l u r i s r u o r t w i m o s n d m i e r e s l i i u n o e m w e w a f a o e g y b d n y y n r e d e g m d n g n e b n e o y e n l 01 TBM 0 0 0 0 0 1 0 0 02 TLP 0 0 0 0 0 0 0 0 03 DDD 0 0 0 0 1 0 0 0 0 0 0 04 LMM 0 0 0 0 0 0 0 0 05 HDS 0 0 0 0 0 0 0 1 0 0 0 06 SPP 0 0 1 0 0 0 0 0 07 OMH 0 0 0 1 0 0 0 0 08 JSC 0 0 0 0 1 0 0 0 0 09 HBD 0 0 1 0 0 0 0 0 0 0 0 10 JAJ 0 0 0 0 0 0 1 0 0 0 1 11 OMM 0 0 0 0 0 0 0 0 12 OWF 0 0 0 0 1 0 0 0 0 0 13 RRS 0 0 0 1 0 0 0 0 0 0 14 ASO 0 0 0 0 0 1 0 0 0 15 PCD 0 0 0 0 0 0 1 0 0 0 0 1 0 16 PPG 0 0 0 1 0 0 0 0 0 0 0 17 FEC 0 0 0 0 0 1 0 0 0 0 18 HTP 0 0 0 0 0 1 0 0 0 0 0 21 LAU 0 0 0 0 0 1 0 1 0 0 0 0 22 HLH 0 0 0 0 0 0 0 0 23 MTB 0 0 0 1 0 0 0 0 0 0 0 25 WOW 0 0 0 0 0 0 0 0 26 SBS 1 0 0 0 0 0 0 0 1 0 0 27 CBC 0 0 1 0 0 0 0 0 0 28 BBB 0 0 0 1 0 0 0 0 1 0 0 29 LFW 1 0 0 0 0 0 0 0 0 30 HDD 0 0 0 0 0 0 1 1 0 0 0 0 0 32 JGF 0 0 0 0 0 0 1 0 0 0 0 0 33 BFP 0 0 0 0 0 0 1 0 0 0 35 SSS 0 0 0 1 0 0 0 0 1 0 0 36 LTT 0 0 0 0 0 0 0 0 37 MBB 0 0 0 0 1 0 0 0 0 38 YLS 0 0 0 0 0 1 0 0 0 39 LCS 0 0 0 0 1 0 0 0 0 0 1 0 0 41 OKC 0 0 0 0 0 0 0 1 0 0 0 42 BBC 0 0 0 1 0 0 0 0 0 43 HHD 0 0 0 0 0 0 1 0 0 0 0 44 HLH 0 0 0 0 0 1 0 0 0 0 0 1 1 45 BBB 0 0 1 0 0 0 0 0 0 0 46 TTP 0 0 0 0 0 1 0 0 0 47 CCM 0 0 0 0 1 0 0 0 0 48 OTB 0 0 0 0 0 0 0 0 49 WLG 0 0 1 0 0 0 0 0 0 1 0 0 0 50 LJH 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
mtf 1 a b f l b r b c c c c i g w a b b b r i r c h l l c r d f g r h h a w a a b b e g o b a i e o o o c c d i d e a d u i e i i y a b c a a k e o a h w u k l a t c w r u a s o a l l l r e g l s y y k d g e d y d t n y e d n h k n y t y h g t l e l l n h l h m m o r t t w o k l l m e o m t n p o s h h t t w o w u i a a a m r n o h o o p p l u r i s r u o r t w i m o s n d m i e r e s l i i u n o e m w e w a f a o e g y b d n y y n r e d e g m d n g n e b n e o y e n l 01 TBM 0 0 0 0 0 0 0 0 02 TLP 0 0 0 0 0 0 0 0 03 DDD 0 0 0 0 1 0 0 0 0 0 0 04 LMM 0 1 0 0 0 0 0 0 1 0 0 0 05 HDS 0 0 0 0 0 0 0 1 0 0 0 06 SPP 0 0 0 0 0 0 0 0 07 OMH 0 0 0 1 0 0 0 0 0 1 0 0 0 0 08 JSC 0 0 0 0 0 0 0 0 09 HBD 0 0 1 0 0 0 0 0 0 0 0 10 JAJ 0 0 0 0 0 0 0 1 0 0 0 11 OMM 0 0 0 0 0 0 0 0 12 OWF 0 0 0 0 0 0 0 0 13 RRS 0 0 0 1 0 0 0 0 0 0 14 ASO 0 0 0 0 0 0 0 1 0 0 0 15 PCD 0 0 0 0 0 0 1 0 0 0 0 0 16 PPG 0 0 0 0 0 0 0 0 17 FEC 0 0 0 0 0 1 0 0 0 0 18 HTP 0 0 0 0 0 0 1 0 0 0 0 0 21 LAU 0 0 0 0 0 1 0 0 0 0 0 0 22 HLH 0 0 0 0 0 0 0 0 23 MTB 0 0 0 1 0 0 0 0 0 0 0 25 WOW 0 0 0 0 0 0 0 0 26 SBS 0 0 1 0 0 0 0 0 0 0 0 27 CBC 0 0 1 0 0 0 0 0 0 0 0 28 BBB 0 0 0 0 1 0 0 0 0 29 LFW 0 1 0 0 0 0 0 0 0 30 HDD 0 1 0 0 0 0 0 0 1 0 0 0 32 JGF 0 0 0 0 0 0 1 0 0 0 0 0 33 BFP 0 0 0 0 0 0 0 0 35 SSS 0 0 0 1 0 0 0 0 0 36 LTT 0 0 0 0 0 0 0 0 37 MBB 0 0 0 0 0 0 0 0 38 YLS 0 0 0 0 0 0 0 0 39 LCS 0 1 0 0 0 0 0 0 0 41 OKC 0 0 0 0 0 0 0 0 42 BBC 0 0 0 1 0 0 0 0 0 0 0 43 HHD 0 0 0 0 0 0 1 0 0 0 0 44 HLH 0 0 0 0 0 0 0 0 45 BBB 0 0 0 1 0 0 0 0 0 46 TTP 0 1 0 0 0 0 0 1 0 0 0 0 0 47 CCM 0 0 0 0 1 0 0 0 0 48 OTB 0 0 0 0 0 0 0 0 49 WLG 0 0 0 0 0 0 0 0 50 LJH 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
mtf 2 a b f l b r b c c c c i g w a b b b r i r c h l l c r d f g r h h a w a a b b e g o b a i e o o o c c d i d e a d u i e i i y a b c a a k e o a h w u k l a t c w r u a s o a l l l r e g l s y y k d g e d y d t n y e d n h k n y t y h g t l e l l n h l h m m o r t t w o k l l m e o m t n p o s h h t t w o w u i a a a m r n o h o o p p l u r i s r u o r t w i m o s n d m i e r e s l i i u n o e m w e w a f a o e g y b d n y y n r e d e g m d n g n e b n e o y e n l 01 TBM 0 0 0 0 0 1 0 0 02 TLP 0 0 0 0 0 0 0 0 03 DDD 0 0 0 0 0 0 0 0 04 LMM 0 0 0 0 0 0 0 0 05 HDS 0 0 0 0 0 0 0 0 06 SPP 0 0 1 0 0 0 0 0 07 OMH 0 0 0 0 0 0 0 0 08 JSC 0 0 0 0 1 0 0 0 09 HBD 0 0 0 0 0 0 0 0 10 JAJ 0 0 0 1 0 0 0 0 0 1 11 OMM 0 0 0 0 0 0 0 0 12 OWF 0 0 0 0 1 0 0 0 0 0 13 RRS 0 0 0 0 0 0 0 0 14 ASO 0 0 0 0 0 1 0 0 0 15 PCD 0 0 0 0 0 0 0 0 1 0 16 PPG 0 0 0 1 0 0 0 0 0 0 0 17 FEC 0 0 0 0 0 0 0 0 18 HTP 0 0 0 0 0 1 0 0 0 0 0 0 21 LAU 0 0 0 1 0 0 0 0 0 0 0 22 HLH 0 0 0 0 0 0 0 0 23 MTB 0 0 0 0 0 0 0 0 25 WOW 0 0 0 0 0 0 0 0 26 SBS 1 0 0 0 0 0 0 0 1 0 0 27 CBC 0 0 0 0 0 1 0 0 0 28 BBB 0 0 0 1 0 0 0 0 0 0 1 0 0 29 LFW 1 0 0 0 0 0 0 0 0 30 HDD 0 0 0 0 0 0 1 0 0 0 0 0 32 JGF 0 0 0 0 0 0 0 1 0 0 0 33 BFP 0 0 0 0 0 0 1 0 0 0 35 SSS 0 0 0 0 0 0 1 0 0 0 0 36 LTT 0 0 0 0 0 0 0 0 37 MBB 0 0 0 0 1 0 0 0 0 38 YLS 0 0 0 0 0 1 0 0 0 39 LCS 0 0 0 0 0 0 0 0 1 0 0 41 OKC 0 0 0 0 0 0 0 0 42 BBC 0 0 0 0 1 0 0 0 0 0 43 HHD 0 0 0 0 0 0 0 0 44 HLH 0 0 0 0 0 1 0 0 0 0 0 1 1 45 BBB 0 0 1 0 0 0 0 0 0 0 0 46 TTP 0 0 0 0 0 0 0 0 47 CCM 0 0 0 0 0 0 0 0 48 OTB 0 0 0 0 0 0 0 0 49 WLG 0 0 1 0 0 0 0 0 0 1 0 0 0 50 LJH 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
mtf 3 a b f l b r b c c c c i g w a b b b r i r c h l l c r d f g r h h a w a a b b e g o b a i e o o o c c d i d e a d u i e i i y a b c a a k e o a h w u k l a t c w r u a s o a l l l r e g l s y y k d g e d y d t n y e d n h k n y t y h g t l e l l n h l h m m o r t t w o k l l m e o m t n p o s h h t t w o w u i a a a m r n o h o o p p l u r i s r u o r t w i m o s n d m i e r e s l i i u n o e m w e w a f a o e g y b d n y y n r e d e g m d n g n e b n e o y e n l 01 TBM 0 0 0 0 0 0 0 0 02 TLP 0 0 0 0 0 0 0 0 03 DDD 0 0 0 0 0 0 0 0 04 LMM 0 0 0 0 0 0 0 0 05 HDS 0 0 0 0 0 0 0 0 06 SPP 0 0 0 0 0 0 0 0 07 OMH 0 0 0 0 0 0 1 0 0 0 0 08 JSC 0 0 0 0 0 0 0 0 09 HBD 0 0 0 0 0 0 0 0 10 JAJ 0 0 0 0 0 0 0 0 11 OMM 0 0 0 0 0 0 0 0 12 OWF 0 0 0 0 0 0 0 0 13 RRS 0 0 0 0 0 0 0 0 14 ASO 0 0 0 0 0 0 0 0 15 PCD 0 0 0 0 0 0 0 0 16 PPG 0 0 0 0 0 0 0 0 17 FEC 0 0 0 0 0 0 0 0 18 HTP 0 0 0 0 0 0 0 0 21 LAU 0 0 0 0 0 0 0 0 22 HLH 0 0 0 0 0 0 0 0 23 MTB 0 0 0 0 0 0 0 0 25 WOW 0 0 0 0 0 0 0 0 26 SBS 0 0 1 0 0 0 0 0 0 0 0 27 CBC 0 0 0 0 0 0 0 0 28 BBB 0 0 0 0 0 0 0 0 29 LFW 0 0 0 0 0 0 0 0 30 HDD 0 0 0 0 0 0 0 0 32 JGF 0 0 0 0 0 0 0 1 0 0 0 33 BFP 0 0 0 0 0 0 0 0 35 SSS 0 0 0 0 0 0 0 0 36 LTT 0 0 0 0 0 0 0 0 37 MBB 0 0 0 0 1 0 0 0 0 38 YLS 0 0 0 0 0 0 0 0 39 LCS 0 0 0 0 0 1 0 0 0 0 41 OKC 0 0 0 0 0 0 0 0 42 BBC 0 0 0 0 0 0 0 0 43 HHD 0 0 0 0 0 0 0 0 44 HLH 0 0 0 0 0 0 0 0 45 BBB 0 0 0 0 0 0 0 0 46 TTP 0 0 0 0 0 0 0 0 47 CCM 0 0 0 0 0 0 0 0 48 OTB 0 0 0 0 0 0 0 0 49 WLG 0 0 0 0 0 0 0 0 50 LJH 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
mtf 4 a b f l b r b c c c c i g w a b b b r i r c h l l c r d f g r h h a w a a b b e g o b a i e o o o c c d i d e a d u i e i i y a b c a a k e o a h w u k l a t c w r u a s o a l l l r e g l s y y k d g e d y d t n y e d n h k n y t y h g t l e l l n h l h m m o r t t w o k l l m e o m t n p o s h h t t w o w u i a a a m r n o h o o p p l u r i s r u o r t w i m o s n d m i e r e s l i i u n o e m w e w a f a o e g y b d n y y n r e d e g m d n g n e b n e o y e n l 01 TBM 0 0 0 0 0 0 0 0 02 TLP 0 0 0 0 0 0 0 0 03 DDD 0 0 0 0 0 0 0 0 04 LMM 0 0 0 0 0 0 0 0 05 HDS 0 0 0 0 0 0 0 0 06 SPP 0 0 0 0 0 0 0 0 07 OMH 0 0 0 0 0 0 0 0 08 JSC 0 0 0 0 0 0 0 0 09 HBD 0 0 0 0 0 0 0 0 10 JAJ 0 0 0 0 0 0 0 0 11 OMM 0 0 0 0 0 0 0 0 12 OWF 0 0 0 0 0 0 0 0 13 RRS 0 0 0 0 0 0 0 0 14 ASO 0 0 0 0 0 0 0 0 15 PCD 0 0 0 0 0 0 0 0 16 PPG 0 0 0 0 0 0 0 0 17 FEC 0 0 0 0 0 0 0 0 18 HTP 0 0 0 0 0 0 0 0 21 LAU 0 0 0 0 0 0 0 0 22 HLH 0 0 0 0 0 0 0 0 23 MTB 0 0 0 0 0 0 0 0 25 WOW 0 0 0 0 0 0 0 0 26 SBS 0 0 0 0 0 0 0 0 27 CBC 0 0 0 0 0 0 0 0 28 BBB 0 0 0 0 0 0 0 0 29 LFW 0 0 0 0 0 0 0 0 30 HDD 0 0 0 0 0 0 0 0 32 JGF 0 0 0 0 0 0 0 0 33 BFP 0 0 0 0 0 0 0 0 35 SSS 0 0 0 0 0 0 0 0 36 LTT 0 0 0 0 0 0 0 0 37 MBB 0 0 0 0 0 0 0 0 38 YLS 0 0 0 0 0 0 0 0 39 LCS 0 0 0 0 0 0 0 0 41 OKC 0 0 0 0 0 0 0 1 0 0 0 42 BBC 0 0 0 0 0 0 0 0 43 HHD 0 0 0 0 0 0 0 0 44 HLH 0 0 0 0 0 0 0 0 45 BBB 0 0 0 0 0 0 0 0 46 TTP 0 0 0 0 0 0 0 0 47 CCM 0 0 0 0 0 0 0 0 48 OTB 0 0 0 0 0 0 0 0 49 WLG 0 0 0 0 0 0 0 0 50 LJH 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
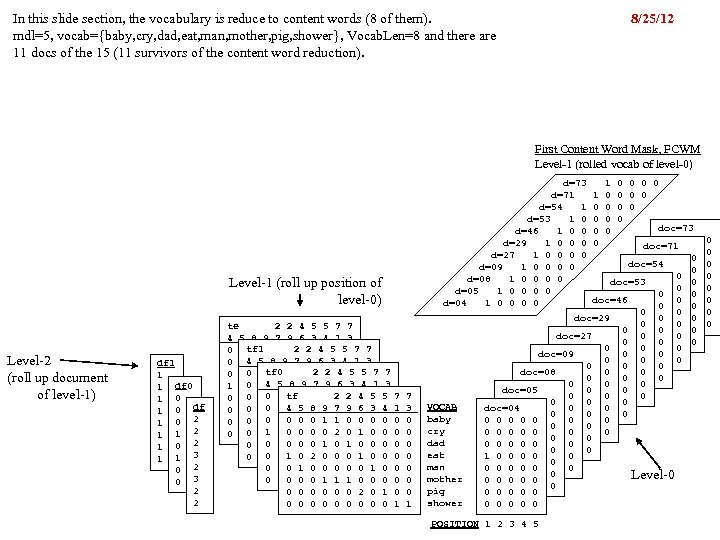In this slide section, the vocabulary is reduce to content words (8 of them). 8/25/12 mdl=5, vocab={baby, cry, dad, eat, man, mother, pig, shower}, Vocab. Len=8 and there are 11 docs of the 15 (11 survivors of the content word reduction). First Content Word Mask, FCWM Level-1 (rolled vocab of level-0) Level-1 (roll up position of level-0) Level-2 (roll up document of level-1) df 1 1 1 df 0 1 0 df 1 0 2 1 1 2 1 0 2 1 1 3 0 2 0 3 2 2 te 2 2 4 5 5 7 7 4 5 8 9 7 9 6 3 4 1 3 tf 1 2 2 4 5 5 0 0 0 1 1 0 0 0 7 7 4 5 8 9 7 9 6 3 4 0 0 1 0 0 0 0 1 3 tf 0 2 2 4 5 0 0 0 0 1 0 0 0 5 7 7 4 5 8 9 7 9 6 3 4 1 3 0 0 1 0 0 0 1 0 0 tf 2 2 0 0 0 1 1 0 0 0 0 0 1 0 0 0 4 5 5 7 7 4 5 8 9 7 9 6 3 4 0 0 0 1 3 0 0 1 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 2 0 1 0 0 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 2 0 0 0 1 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 2 0 1 0 0 0 1 1 d=73 1 0 0 d=71 1 0 0 d=54 1 0 0 d=53 1 0 0 doc=73 d=46 1 0 0 0 0 0 d=29 1 0 0 doc=71 0 0 0 d=27 1 0 0 0 0 0 doc=54 0 0 0 d=09 1 0 0 0 0 0 d=08 1 0 0 doc=53 0 0 0 0 d=05 1 0 0 0 0 doc=460 0 0 0 0 d=04 1 0 0 0 0 0 0 0 0 doc=290 0 0 0 1 0 0 0 0 0 0 doc=270 0 0 0 1 0 0 0 0 0 1 0 0 0 0 doc=090 1 0 0 0 0 0 0 0 1 0 0 0 0 doc=080 0 0 0 0 0 0 0 0 1 1 0 0 0 doc=050 1 0 0 0 0 0 0 0 0 0 VOCAB doc=040 0 0 0 1 0 0 0 0 baby 0 0 0 1 1 0 0 0 0 1 0 0 cry 0 0 0 0 0 0 0 dad 0 0 0 0 0 1 0 0 0 0 0 eat 1 0 0 0 0 man 0 0 0 0 Level-0 mother 0 0 0 0 0 pig 0 0 0 shower 0 0 0 POSITION 1 2 3 4 5
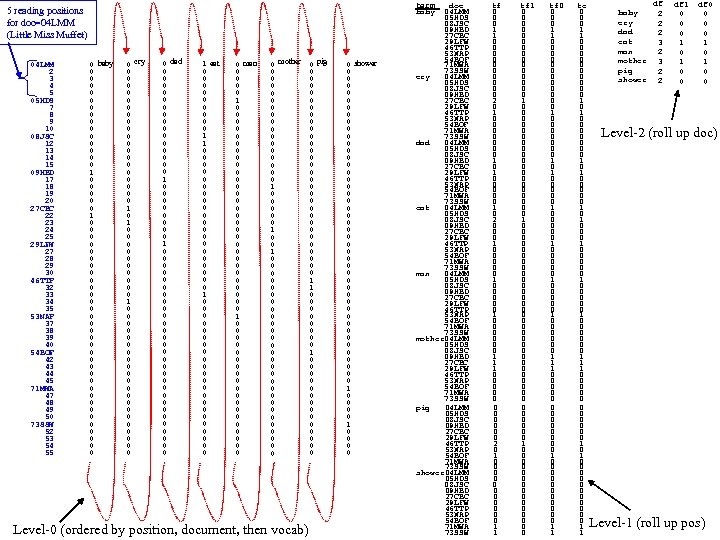5 reading positions for doc=04 LMM (Little Miss Muffet) 04 LMM 2 3 4 5 05 HDS 7 8 9 10 08 JSC 12 13 14 15 09 HBD 17 18 19 20 27 CBC 22 23 24 25 29 LFW 27 28 29 30 46 TTP 32 33 34 35 53 NAP 37 38 39 40 54 BOF 42 43 44 45 71 MWA 47 48 49 50 73 SSW 52 53 54 55 0 baby 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 cry 0 0 0 0 0 1 0 0 0 0 0 0 0 0 dad 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 eat 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 man 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 mother 0 pig 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 Level-0 (ordered by position, document, then vocab) 0 shower 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 term doc tf 1 tf 0 te baby 04 LMM 0 0 05 HDS 0 0 08 JSC 0 0 09 HBD 1 0 1 1 27 CBC 1 0 1 1 29 LFW 0 0 46 TTP 0 0 53 NAP 0 0 54 BOF 0 0 71 MWA 0 0 73 SSW 0 0 cry 04 LMM 0 0 05 HDS 0 0 08 JSC 0 0 09 HBD 0 0 27 CBC 2 1 0 1 29 LFW 0 0 46 TTP 1 0 1 1 53 NAP 0 0 54 BOF 0 0 71 MWA 0 0 73 SSW 0 0 dad 04 LMM 0 0 05 HDS 0 0 08 JSC 0 0 09 HBD 1 0 1 1 27 CBC 0 0 29 LFW 1 0 1 1 46 TTP 0 0 53 NAP 0 0 54 BOF 0 0 71 MWA 0 0 73 SSW 0 0 eat 04 LMM 1 0 1 1 05 HDS 0 0 08 JSC 2 1 0 1 09 HBD 0 0 27 CBC 0 0 29 LFW 0 0 46 TTP 1 0 1 1 53 NAP 0 0 54 BOF 0 0 71 MWA 0 0 73 SSW 0 0 man 04 LMM 0 0 05 HDS 1 0 1 1 08 JSC 0 0 09 HBD 0 0 27 CBC 0 0 29 LFW 0 0 46 TTP 0 0 53 NAP 1 0 1 1 54 BOF 0 0 71 MWA 0 0 73 SSW 0 0 mother 04 LMM 0 0 05 HDS 0 0 08 JSC 0 0 09 HBD 1 0 1 1 27 CBC 1 0 1 1 29 LFW 1 0 1 1 46 TTP 0 0 53 NAP 0 0 54 BOF 0 0 71 MWA 0 0 73 SSW 0 0 pig 04 LMM 0 0 05 HDS 0 0 08 JSC 0 0 09 HBD 0 0 27 CBC 0 0 29 LFW 0 0 46 TTP 2 1 0 1 53 NAP 0 0 54 BOF 1 0 1 1 71 MWA 0 0 73 SSW 0 0 shower 04 LMM 0 0 05 HDS 0 0 08 JSC 0 0 09 HBD 0 0 27 CBC 0 0 29 LFW 0 0 46 TTP 0 0 53 NAP 0 0 54 BOF 0 0 71 MWA 1 0 1 1 73 SSW 1 0 1 1 baby cry dad eat man mother pig shower df 2 2 2 3 2 2 df 1 0 0 0 1 0 0 df 0 0 1 0 0 Level-2 (roll up doc) Level-1 (roll up pos)
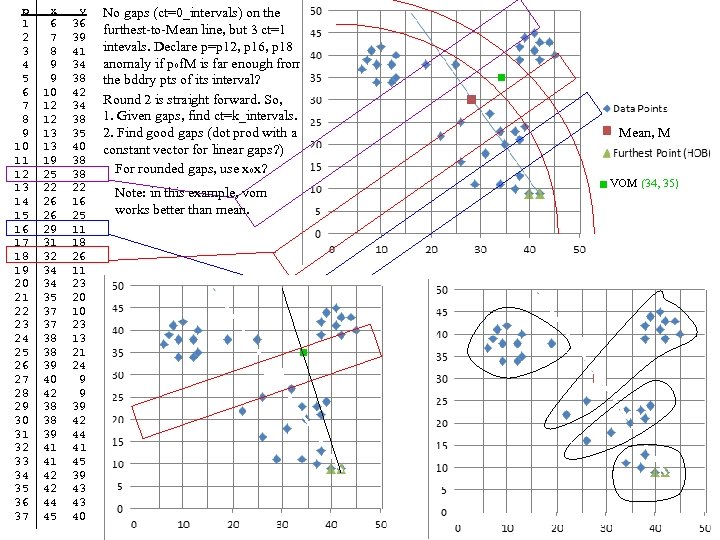p x y 1 6 36 2 7 39 3 8 41 4 9 34 5 9 38 6 10 42 7 12 34 8 12 38 9 13 35 10 13 40 11 19 38 12 25 38 13 22 22 14 26 16 15 26 25 16 29 11 17 31 18 18 32 26 19 34 11 20 34 23 21 35 20 22 37 10 23 37 23 24 38 13 25 38 21 26 39 24 27 40 9 28 42 9 29 38 39 30 38 42 31 39 44 32 41 41 33 41 45 34 42 39 35 42 43 36 44 43 37 45 40 No gaps (ct=0_intervals) on the furthest-to-Mean line, but 3 ct=1 intevals. Declare p=p 12, p 16, p 18 anomaly if pof. M is far enough from the bddry pts of its interval? Round 2 is straight forward. So, 1. Given gaps, find ct=k_intervals. 2. Find good gaps (dot prod with a constant vector for linear gaps? ) For rounded gaps, use xox? Note: in this example, vom works better than mean. Mean, M VOM (34, 35)
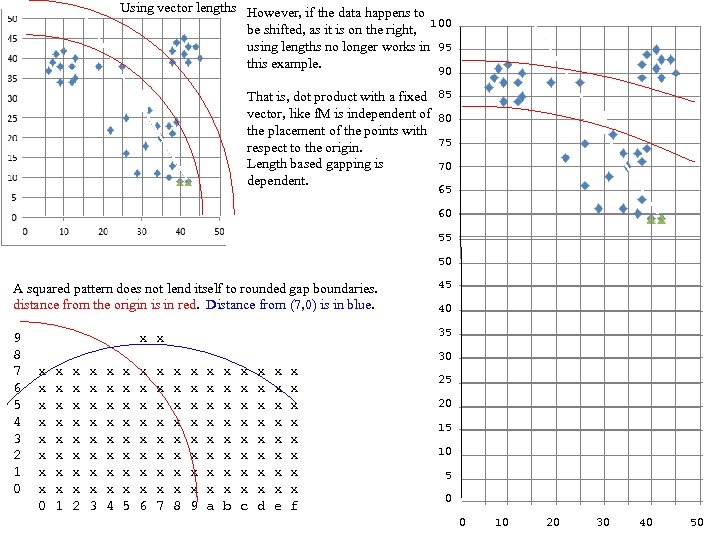Using vector lengths However, if the data happens to be shifted, as it is on the right, 100 using lengths no longer works in 95 this example. 90 That is, dot product with a fixed 85 vector, like f. M is independent of 80 the placement of the points with 75 respect to the origin. Length based gapping is 70 dependent. 65 60 55 50 A squared pattern does not lend itself to rounded gap boundaries. distance from the origin is in red. Distance from (7, 0) is in blue. 45 9 x x 8 7 x x x x 6 x x x x 5 x x x x 4 x x x x 3 x x x x 2 x x x x 1 x x x x x x x x 0 1 2 3 4 5 6 7 8 9 a b c d e f 35 40 30 25 20 15 10 5 0 0 10 20 30 40 50
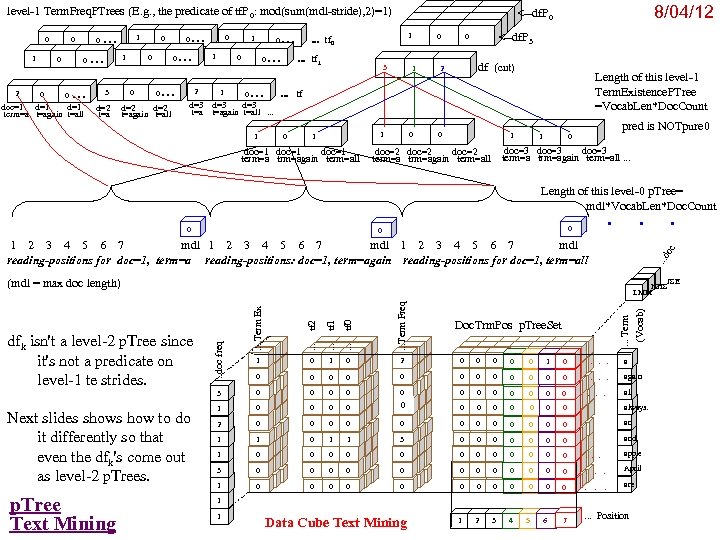level-1 Term. Freq. PTrees (E. g. , the predicate of tf. P 0: mod(sum(mdl-stride), 2)=1) 0 1 2 0 0 1 0 . . . doc=1 d=1 term=a t=again t=all 3 0. . . 0 0. . . d=2 t=again t=all 0 1 2 1 1 1 0. . . tf 0 0 0. . . tf 1 0. . . tf d=3 t=again t=all . . . 1 0 8 3 1 8 8 0 1 1 1 0 3 3 8/04/12 <--df. P 0 3 <--df. P 3 df (cnt) 2 Length of this level-1 Term. Existence. PTree =Vocab. Len*Doc. Count 1 1 0 0 1 1 pred is NOTpure 0 0 doc=3 doc=1 doc=2 term=a trm=again term=all. . . 0 Length of this level-0 p. Tree= mdl*Vocab. Len*Doc. Count . . . 0 0 . . . d oc 1 2 3 4 5 6 7 mdl reading-positions for doc=1, term=a reading-positions: doc=1, term=again reading-positions for doc=1, term=all JSE HHS LMM p. Tree Text Mining . . . tf 0 . . . Term Freq 1 0 2 0 0 0 1 0 . a 0 0 0 . again 0 0 0 . all 1 0 0 0 3 0 0 0 0 always. 2 0 0 0 an 1 1 0 1 1 3 0 0 0 0 and . . . Term (Vocab) . . . tf 1 0 . . doc freq . . . tf 2 Next slides shows how to do it differently so that even the dfk's come out as level-2 p. Trees. 1 3 dfk isn't a level-2 p. Tree since it's not a predicate on level-1 te strides. . Term Ex (mdl = max doc length) Doc. Trm. Pos p. Tree. Set 1 0 0 0 . . . apple 3 0 0 0 . April 1 0 0 0 . are 1 2 3 4 1 1 Data Cube Text Mining 5 6 7 . . . Position
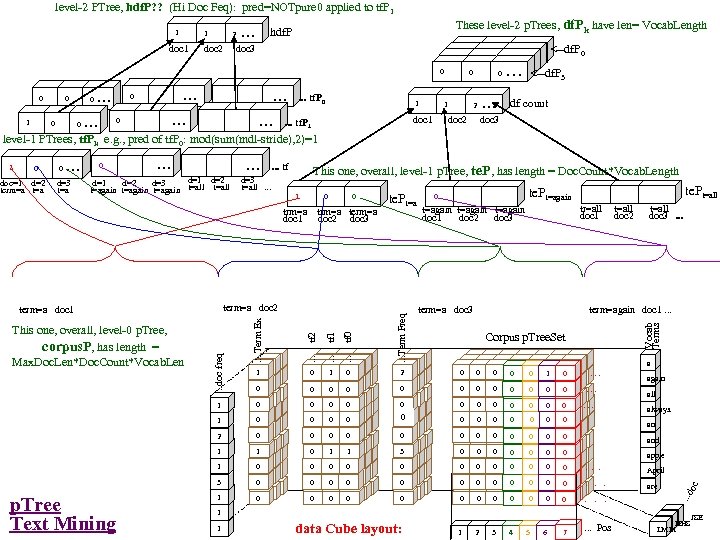level-2 PTree, hdf. P? ? (Hi Doc Feq): pred=NOTpure 0 applied to tf. P 1 1 These level-2 p. Trees, df. Pk have len= Vocab. Length hdf. P 2 . . . 1 doc 2 doc 3 0 0 1 0 0 . . . 0 . . . tf. P 0 1 . . . 8 8 8 0 1 1 1 3 3 3 0 . . . 2 . . . 1 <--df. P 0 <--df. P 3 df count doc 1 doc 2 doc 3 . . . tf. P 1 level-1 PTrees, tf. Pk e. g. , pred of tf. P 0: mod(sum(mdl-stride), 2)=1 0 0 . . . doc=1 d=2 d=3 term=a t=a 0 . . tf d=1 d=2 d=3 t=again t=all . . . This one, overall, level-1 p. Tree, te. P, has length = Doc. Count*Vocab. Length 1 0 0 trm=a term=a doc 1 doc 2 doc 3 term=a doc 2 0 te. Pt=again te. Pt=all tr=all t=all doc 1 doc 2 doc 3 . . . t=again doc 1 doc 2 doc 3 term=a doc 3 . . . tf 0 . . . Term Freq 0 2 0 0 0 1 0 . . . 0 0 0 0 0 0 . . . 0 0 0 3 0 0 0 0 2 0 0 0 1 1 0 1 1 3 0 0 0 0 apple 1 0 0 0 . . . April 3 0 0 0 . are 1 0 0 0 . data Cube layout: 1 2 3 4 Vocab Terms . . . tf 1 1 Corpus p. Tree. Set a 5 6 7 all always. an and 1 1 again . . . Pos . . . doc freq 0 1 p. Tree Text Mining 1 1 This one, overall, level-0 p. Tree, corpus. P, has length = Max. Doc. Len*Doc. Count*Vocab. Len . . . tf 2 term=again doc 1. . . Term Ex term=a doc 1 te. Pt=a oc 2 JSE HHS LMM
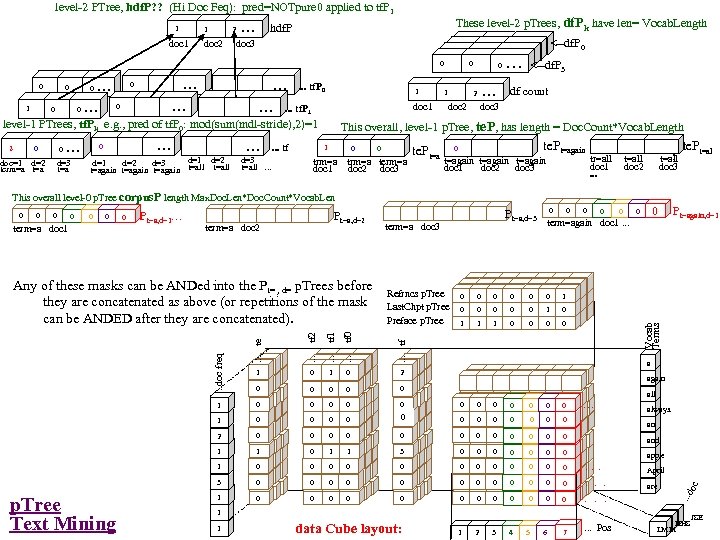level-2 PTree, hdf. P? ? (Hi Doc Feq): pred=NOTpure 0 applied to tf. P 1 1 These level-2 p. Trees, df. Pk have len= Vocab. Length hdf. P 2 . . . 1 doc 2 doc 3 0 0 1 0 0 . . . 0 . . . tf. P 0 1 . . . doc=1 d=2 d=3 term=a t=a . . . 0 0 . . . tf d=1 d=2 d=3 t=again t=all . . . 8 8 0 1 1 1 3 3 0 . . . <--df. P 3 df count 2 . . . 1 <--df. P 0 3 doc 1 doc 2 doc 3 . . . tf. P 1 level-1 PTrees, tf. Pk e. g. , pred of tf. P 0: mod(sum(mdl-stride), 2)=1 2 8 This overall, level-1 p. Tree, te. P, has length = Doc. Count*Vocab. Length 1 0 0 te. Pt=a trm=a term=a doc 1 doc 2 doc 3 0 te. Pt=again t=again doc 1 doc 2 doc 3 te. Pt=al l tr=all t=all doc 1 doc 2 doc 3 . . . This overall level-0 p. Tree corpus. P length Max. Doc. Len*Doc. Count*Vocab. Len 0 0 term=a doc 1 0 Pt=a, d=1. . . Pt=a, d=2 term=a doc 3 0 0 0 Pt=again, d=1 0 0 0 0 0 1 1 1 0 0 1 0 2 0 0 0 1 0 0 0 . . . 1 0 0 0 3 0 0 0 0 2 0 0 0 1 1 0 1 1 3 0 0 0 0 apple 1 0 0 0 . . . April 3 0 0 0 . are 1 0 0 0 . data Cube layout: 1 2 3 4 p. Tree Text Mining a again all an and 1 1 5 6 7 always. . Pos . . . doc freq . . . tf 0 0 . . . tf 1 0 . . . tf 2 Refrncs p. Tree Last. Chpt p. Tree Preface p. Tree 0 term=again doc 1. . . te Any of these masks can be ANDed into the Pt= , d= p. Trees before they are concatenated as above (or repetitions of the mask can be ANDED after they are concatenated). Pt=a, d=3 oc 0 Vocab Terms 0 JSE HHS LMM
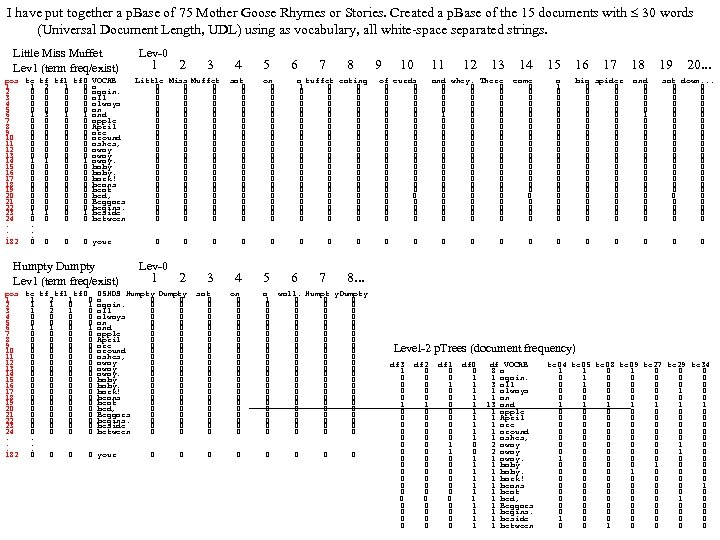I have put together a p. Base of 75 Mother Goose Rhymes or Stories. Created a p. Base of the 15 documents with 30 words (Universal Document Length, UDL) using as vocabulary, all white-space separated strings. Little Miss Muffet Lev 1 (term freq/exist) pos 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24. . . 182 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20. . . te tf tf 1 tf 0 VOCAB Little Miss Muffet sat on a tuffet eating of curds and whey. There came a big spider and sat down. . . 1 2 1 0 a 0 0 0 0 0 1 0 0 0 0 0 0 0 again. 0 0 0 0 0 0 0 0 all 0 0 0 0 0 0 0 0 always 0 0 0 0 0 0 0 0 an 0 0 0 0 0 1 3 1 1 and 0 0 0 0 0 1 0 0 0 0 apple 0 0 0 0 0 0 0 0 April 0 0 0 0 0 0 0 0 are 0 0 0 0 0 0 0 0 around 0 0 0 0 0 0 0 0 ashes, 0 0 0 0 0 0 0 0 0 0 0 0 0 away 0 0 0 0 0 1 1 0 1 away. 0 0 0 0 0 0 0 0 0 0 0 0 0 baby. 0 0 0 0 0 0 0 0 bark! 0 0 0 0 0 0 0 0 beans 0 0 0 0 0 0 0 0 beat 0 0 0 0 0 0 0 0 bed, 0 0 0 0 0 0 0 0 Beggars 0 0 0 0 0 0 0 0 begins. 0 0 0 0 0 1 1 0 1 beside 0 0 0 0 0 0 0 0 between 0 0 0 0 0 . 0 0 0 0 your 0 0 0 0 0 Humpty Dumpty Lev 1 (term freq/exist) pos 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24. . . 182 Lev-0 1 2 3 4 5 6 7 8. . . te tf tf 1 tf 0 05 HDS Humpty Dumpty sat on a wall. Humpt y. Dumpty 1 2 1 0 a 0 0 1 0 0 0 1 1 0 1 again. 0 0 0 0 1 2 1 0 all 0 0 0 0 0 0 always 0 0 0 0 0 0 an 0 0 0 0 1 1 0 1 and 0 0 0 0 0 0 apple 0 0 0 0 0 0 April 0 0 0 0 0 0 are 0 0 0 0 0 0 around 0 0 0 0 0 0 ashes, 0 0 0 0 0 0 away 0 0 0 0 0 0 away. 0 0 0 0 0 0 baby. 0 0 0 0 0 0 bark! 0 0 0 0 0 0 beans 0 0 0 0 0 0 beat 0 0 0 0 0 0 bed, 0 0 0 0 0 0 Beggars 0 0 0 0 0 0 begins. 0 0 0 0 0 0 beside 0 0 0 0 0 0 between 0 0 0 0 . . . 0 0 your 0 0 0 0 Level-2 p. Trees (document frequency) df 3 df 2 df 1 df 0 df VOCAB te 04 te 05 te 08 te 09 te 27 te 29 te 34 1 0 0 0 8 a 1 1 0 0 1 1 again. 0 1 0 0 1 1 3 all 0 1 0 0 1 1 always 0 0 0 1 1 an 0 0 1 1 0 1 13 and 1 1 0 0 0 1 1 apple 0 0 0 1 1 April 0 0 0 1 1 are 0 0 0 1 1 around 0 0 0 1 1 ashes, 0 0 0 1 0 2 away 0 0 0 1 0 0 1 1 away. 1 0 0 0 1 1 baby 0 0 1 0 0 0 1 1 baby. 0 0 0 1 1 bark! 0 0 0 1 1 beans 0 0 0 1 1 beat 0 0 0 0 0 1 1 bed, 0 0 0 1 1 Beggars 0 0 0 1 1 begins. 0 0 0 1 1 beside 1 0 0 0 1 1 between 0 0 1 0 0
Latent semantic indexing (LSI) is indexing and retrieval that uses Singular value decomposition for patterns in terms and concepts in text. LSI is based on the principle that words that are used in the same contexts tend to have similar meanings. LSI feature: ability to extract conceptual content of a body of text by establishing associations between terms that occur in similar contexts. [1] LSI overcomes synonymy, polysemy which cause mismatches in info retrieval [3] and cause Boolean keyword queries to mess up. LSI performs autodoc categorization (assignment of docs to predefined categories based on similarity to conceptual content of the categories. [5] LSI uses example docs for conceptual basis categories - concepts are compared to the concepts contained in the example items, and a category (or categories) is assigned to the docs based on similarities between concepts they contain and the concepts contained in example docs. Mathematics of LSI (linear algebra techniques to learn the conceptual correlations in a collection of text). Construct a weighted term-document matrix, do Singular Value Decomposition on it. Use that to identify the concepts contained in the text. Term Document Matrix, A: Each (of m) terms represented by a row, each (of n) doc is rep'ed by a column, with each matrix cell, aij, initially representing number of times the associated term appears in the indicated document, tfij. This matrix is usually large and very sparse. Once a term-document matrix is constructed, local and global weighting functions can be applied to it to condition the data. local: [13] Binary if term exists in the doc Term. Frequency; global weighting functions: Binary Normal Gf. Idf, Idf Entropy Mathematics of LSI (linear algebra techniques to learn the conceptual correlations in a collection of text). Construct a weighted term-document matrix, do Singular Value Decomposition on it. Use that to identify the concepts contained in the text. Term Document Matrix, A: Each (of m) term represented by a row, each (of n) doc is rep'ed by a column, with each matrix cell, aij, initially representing number of times the associated term appears in the indicated document, tfij. This matrix is usually large and very sparse. SVD basically reduces the dimensionality of the matrix to a tractable size by finding the singular values. It involves matrix operations and may not be amenable to p. Tree operations (i. e. horizontal methods are highly developed and my be best. We should study it though to see if we can identify a p. Tree based breakthrough for creating the reduction that SVD achieves. Is a new SVD program run required for every new query? or is it a one time thing? If it is one-time, there is probably little advantage in searching for p. Tree speedups? If and when it is not a one-time application to the original data, p. Tree speedups my hold promise. Even if it is one-time, we might take the point of view that we do the SVD reduction (using standard horizontal methods) and then covert the result to vertical p. Trees for the data mining (which would be done over and over again). That p. Tree-ization of the end result of the SVD reduction could be organized as in the previous slides. Here is a good paper on the subject of LSI and SVD: http: //www. cob. unt. edu/itds/faculty/evengelopoulos/dsci 5910/LSA_Deerwester 1990. pdf Thoughts for the future: I am now convinced we can do LSI using p. Tree processing. The heart of LSI is SVD. The heart of SVD is Gaussian Elimination (which is adding a constant times a matrix row to another row - which we can do with p. Trees). We will talk more about this next Saturday and during the week.
SVD: Let X be the t by d Term. Frequency (tf) matrix. It can be decomposed as T 0 S 0 D 0 T where T and D have ortho-normal columns and S has only the singular values on its diagonal in descending order. Remove from T 0, S 0, D 0, row-col of all but highest k singular values, giving T, S, D. X ~= X^ ≡ TSDT (X^ is the rank=k matrix closest to X). We have reduced the dimension from rank(X) to k and we note, X^X^T = TS 2 TT and X^TX^ = DS 2 DT There are three sorts of comparisons of interest: Comparing 1. terms (how similar are terms, i and j? ) (comparing rows) 2. documents (how similar are documents i and j? ) (comparing documents) 3. terms and documents (how associated are term i and doc j? ) (examining individual cells) Comparing terms (how similar are terms, i and j? ) (comparing rows) Dot product between two rows of X^ reflects their similarity (similar occurrence pattern across the documents). X^X^T is the square t x t symmetric matrix containing all these dot products. X^X^T = TS 2 TT This means the ij cell in X^X^T is the dot prod of i and j rows of TS (rows TS can be considered coords of terms). Comparing documents (how similar are documents, i and j? ) (comparing columns) Dot product of two columns of X^ reflects their similarity (extent to which two documents have a similar profile of terms). X^TX^ is the square d x d symmetric matrix containing all these dot products. X^TX^ = DS 2 DT This means the ij cell in X^TX^ is the dot prod of i and j columns of DS (considered coords of documents). Comparing a term and a document (how associated are term i and document j? ) (analyzing cell i, j of X^) Since X^ = TSDT cell ij is the dot product of the ith row of TS½ and the jth column of DS½
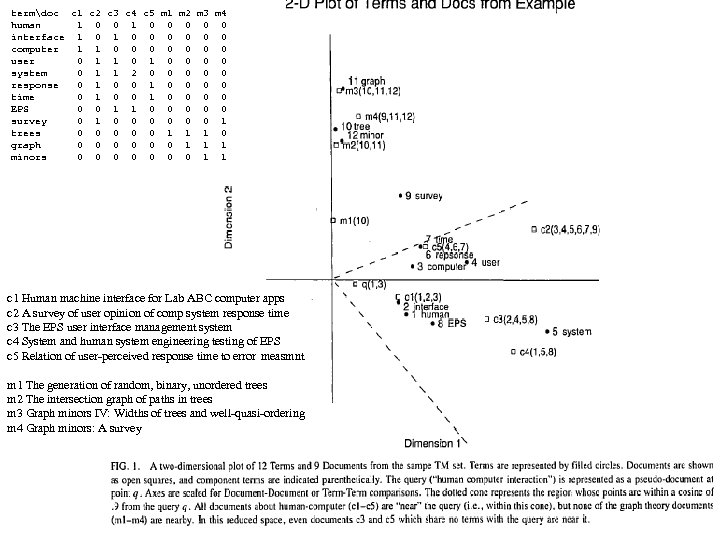termdoc c 1 c 2 c 3 c 4 c 5 m 1 m 2 m 3 m 4 human 1 0 0 0 0 0 interface 1 0 0 0 0 computer 1 1 0 0 0 0 user 0 1 1 0 0 0 0 system 0 1 1 2 0 0 0 response 0 1 0 0 0 0 time 0 1 0 0 0 0 EPS 0 0 1 1 0 0 0 survey 0 1 0 0 0 1 trees 0 0 0 1 1 1 0 graph 0 0 0 1 1 1 minors 0 0 0 0 1 1 c 1 Human machine interface for Lab ABC computer apps c 2 A survey of user opinion of comp system response time c 3 The EPS user interface management system c 4 System and human system engineering testing of EPS c 5 Relation of user-perceived response time to error measmnt m 1 The generation of random, binary, unordered trees m 2 The intersection graph of paths in trees m 3 Graph minors IV: Widths of trees and well-quasi-ordering m 4 Graph minors: A survey
termdoc c 1 c 2 c 3 c 4 c 5 m 1 m 2 m 3 m 4 human 1 0 0 0 0 0 interface 1 0 0 0 0 computer 1 1 0 0 0 0 user 0 1 1 0 0 0 0 system 0 1 1 2 0 0 0 response 0 1 0 0 0 0 time 0 1 0 0 0 0 EPS 0 0 1 1 0 0 0 survey 0 1 0 0 0 1 trees 0 0 0 1 1 1 0 graph 0 0 0 1 1 1 minors 0 0 0 0 1 1 X = T 0 S 0 D 0 T T 0 D 0 col-orthonormal. Approx X keeping only 1 st 2 singular values and corresp cols of T, D which are coords used to position terms and docs in 2 D rep above. In this reduced model: X ~ X^ = TSD T
http: //ocw. mit. edu/courses/mathematics/18 -06 -linear-algebra-spring-2010/tools/
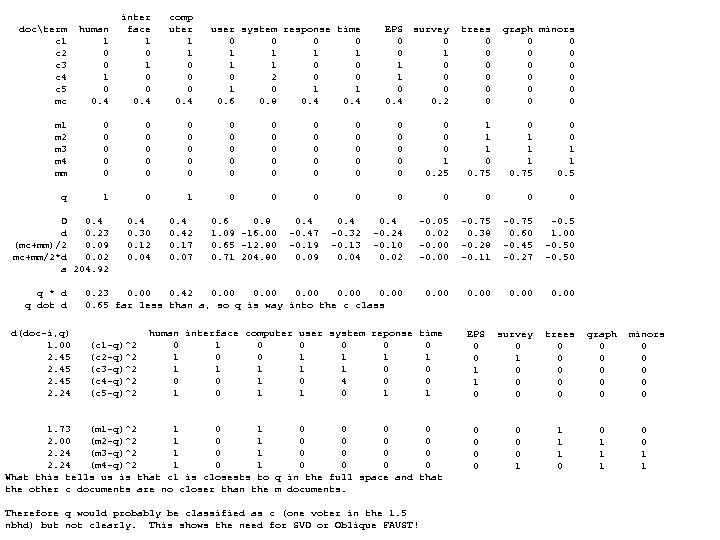inter comp docterm human face uter user system response time EPS c 1 1 0 0 0 c 2 0 0 1 1 1 0 c 3 0 1 1 0 0 1 c 4 1 0 0 0 2 0 0 1 c 5 0 0 0 1 1 0 mc 0. 4 0. 6 0. 8 0. 4 survey trees graph minors 0 0 1 0 0 0 0 0. 2 0 0 0 m 1 0 0 0 0 m 2 0 0 0 0 m 3 0 0 0 0 m 4 0 0 0 0 mm 0 0 0 0 0 1 0 0 0 1 1 1 1 0 1 1 0. 25 0. 75 0. 5 q 1 0 0 0 0 0 D 0. 4 0. 6 0. 8 0. 4 -0. 05 -0. 75 -0. 5 d 0. 23 0. 30 0. 42 1. 09 -16. 00 -0. 47 -0. 32 -0. 24 0. 02 0. 38 0. 60 1. 00 (mc+mm)/2 0. 09 0. 12 0. 17 0. 65 -12. 80 -0. 19 -0. 13 -0. 10 -0. 00 -0. 28 -0. 45 -0. 50 mc+mm/2*d 0. 02 0. 04 0. 07 0. 71 204. 80 0. 09 0. 04 0. 02 -0. 00 -0. 11 -0. 27 -0. 50 a 204. 92 q * d 0. 23 0. 00 0. 42 0. 00 0. 00 q dot d 0. 65 far less than a, so q is way into the c class d(doc-i, q) human interface computer user system reponse time EPS survey trees graph minors 1. 00 (c 1 -q)^2 0 1 0 0 0 0 0 2. 45 (c 2 -q)^2 1 0 0 1 1 0 1 0 0 0 2. 45 (c 3 -q)^2 1 1 1 0 0 0 0 2. 45 (c 4 -q)^2 0 0 1 0 4 0 0 1 0 0 2. 24 (c 5 -q)^2 1 0 1 1 0 0 0 1. 73 (m 1 -q)^2 1 0 0 0 0 1 0 0 2. 00 (m 2 -q)^2 1 0 0 0 0 1 1 0 2. 24 (m 3 -q)^2 1 0 0 0 0 1 1 1 2. 24 (m 4 -q)^2 1 0 0 0 1 0 1 1 What this tells us is that c 1 is closests to q in the full space and that the other c documents are no closer than the m documents. Therefore q would probably be classified as c (one voter in the 1. 5 nbhd) but not clearly. This shows the need for SVD or Oblique FAUST!
Provenance From Wikipedia, the free encyclopedia Jump to: navigation, search For other uses Provenance (disambiguation). 7/7/12 Archaeology: Evidence of provenance can be of importance in archaeology. Fakes are not unknown and finds are sometimes removed from the context in which they were found without documentation, reducing their value to the world of learning. Even when apparently discovered in-situ archaeological finds are treated with caution. The provenance of a find may not be properly represented by the context in which it was found. Artifacts can be moved far from their place of origin by mechanisms that include looting, collecting, theft or trade and further research is often required to establish the true provenance of a find. Paleontology: In paleontology it is recognised that fossils can also move from their primary context and are sometimes found, apparently in-situ, in deposits to which they do not belong, moved by, for example, the erosion of nearby but different outcrops. Most museums make strenuous efforts to record how the works in their collections were acquired and these records are often of use in helping to establish provenance. Seed provenance: Seed provenance refers to the specified area in which plants that produced seed are located or were derived. Data provenance: Scientific research is held to be of good provenance when it is documented in detail sufficient to allow reproducibility. [23] Scientific workflows assist scientists and programmers with tracking their data through all transformations, analyses, and interpretations. Data sets are reliable when the process used to create them are reproducible and analyzable for defects. [24] Current initiatives to effectively manage, share, and reuse ecological data are indicative of the increasing importance of data provenance. Examples of these initiatives are National Science Foundation Datanet projects, Data. ONE and Data Conservancy. Computers and law: The term provenance is used when ascertaining the source of goods such as computer hardware to assess if they are genuine or counterfeit. Chain of custody is an equivalent term used in law, especially for evidence in criminal or commercial cases. Data provenance covers the provenance of computerized data. There are two main aspects of data provenance: ownership of the data and data usage. Ownership will tells the user who is responsible for the source of the data, ideally including information on the originator of the data. Data usage gives details regarding how the data has been used and modified and often includes info on how to cite the data source or sources. Data provenance is of particular concern with electronic data, as data sets are often modified and copied without proper citation or acknowledgement of the originating data set. Databases make it easy to select specific information from data sets and merge this data with other data sources without any documentation of how the data was obtained or how it was modified from the original data set or sets. Secure Provenance refers to providing integrity and confidentiality guarantees to provenance information. In other words, secure provenance means to ensure that history cannot be rewritten, and users can specify who else can look into their actions on the object. [25] See also Dating methodology (archaeology) Post excavation Arnolfini Portrait - fairly full example of the provenance of a painting Annunciation (van Eyck, Washington) - another example Records Management Traceability External links: Look up provenance in Wiktionary, the free dictionary. EU Provenance Project - a technology project that sought to support the electronic certification of data provenance Data. ONE Data Conservancy
APPENDIX: HADOOP Map. Reduce Bad news: lots of programming work Communication and coordination; Recovery from machine failure; Status reporting; Debugging; Optimization; Locality Bad news II: repeat for every problem you want to solve. How can we make it easy to write distributed programs? Data Flow in Map. Reduce: Read a lot of data Map: extract something you care about from each rec. Partition the output – which keys go to which reducer. Shuffle and sort – reducer expects his keys sorted and for each key – list of all values Reduce: aggregate, summarize, filter, or transform. Write the results. Map selects. Reduce does grouping and summing. Example: Word histogram Map(string input_key, string input_value); /*input_key=doc_name, input)value=doc_contents*/ For each word w in input_values: Emit_intermediate(w, *!*); Reduce(string key, Iterator intermediate_value); /*key: a word, same for i/o; intermediate_value a list of counts*/ int result – 0; for each v in intermediate_value: result += Parse. Int(v); Emit(A=String(result)); HADOOP Map. Reduce Example: Inverted Wed Graph For each pg, gen a list of incoming links. Input: Web documents Map: for each link L in doc D emit
Singular Value Decomposition ( http: //mathworld. wolfram. com/Singular. Value. html ) If a matrix has a matrix of eigenvectors that is not invertible (for example, the matrix has the noninvertible system of eigenvectors ), then does not have an eigen decomposition. However, if is an real matrix with , then can be written using a so-called singular value decomposition of the form A = UDVT (1) Note that there are several conflicting notational conventions in use in the literature. Press et al. (1992) define to be an matrix, as , and as . However, Mathematica defines as an , as , and as . In both systems, and have orthogonal columns so that UTU=1 (2) and VTV=1 (3) (where the two identity matrices may have different dimensions), and has entries only along the diagonal. For a complex matrix , the singular value decomposition is a decomposition into the form A = UDV H (4) where U and V are unitary matrices, VH is the conjugate transpose of V, and D is a diagonal matrix whose elements are the singular values of the original matrix. If is a complex matrix, then there always exists such a decomposition with positive singular values ( Golub and Van Loan 1996, pp. 70 and 73). Singular value decomposition is implemented in Mathematica as Singular. Value. Decomposition[m], which returns a list U, D, V , where U and V are matrices and D is a diagonal matrix made up of the singular values of . SEE ALSO: Cholesky Decomposition, Eigen Decomposition Theorem, Eigenvalue, Eigenvector, LU Decomposition, Matrix Decomposition, Matrix Decomposition Theorem, QR Decomposition, Singular Value, Unitary Matrix REFERENCES: Gentle, J. E. "Singular Value Factorization. " § 3. 2. 7 in Numerical Linear Algebra for Applications in Statistics. Springer-Verlag, pp. 102 -103, 98. Golub, G. H. and Van Loan, C. F. "The Singular Value Decomposition" and "Unitary Matrices. " § 2. 5. 3 and 2. 5. 6 in Matrix Computations, 3 rd ed. Baltimore, MD: Johns Hopkins University Press, pp. 70 -71 and 73, 1996. Nash, J. C. "The Singular-Value Decomposition and Its Use to Solve Least-Squares Problems. " Ch. 3 in Compact Numerical Methods for Computers: Linear Algebra and Function Minimisation, 2 nd ed. Bristol, England: Adam Hilger, pp. 30 -48, 1990. Press, W. H. ; Flannery, B. P. ; Teukolsky, S. A. ; and Vetterling, W. T. "Singular Value Decomposition. " § 2. 6 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2 nd ed. Cambridge, England: Cambridge University Press, pp. 51 -63, 1992. CITE THIS AS: Weisstein, Eric W. "SVD. " Math. World--A Wolfram http: //mathworld. wolfram. com/Singular. Value. Decomposition. html Wolfram Web Resources Mathematica » The #1 tool for creating Demonstrations and anything technical. Wolfram|Alpha » Explore anything with the first computational knowledge engine. Wolfram Demonstrations Project » Explore thousands of free applications across science, mathematics, engineering, technology, business, art, finance, social sciences, and more. Computable Document Format » The format that makes Demonstrations (and any information) easy to share and interact with. STEM initiative » Programs & resources for educators, schools & students. Computerbasedmath. org » Join the initiative for modernizing math education. Contact the Math. World Team© 19992012 Wolfram Research, Inc. | Terms of Use THINGS TO TRY: singular value decomposition (28 base 16) + (30 base 5) d/dy f(x^2 + x y +y^2) Image Compression via the Singular Value Decomposition Chris Maes Exploratory Factor Analysis Stuart Nettleton Singular Value Decomposition Chris Maes
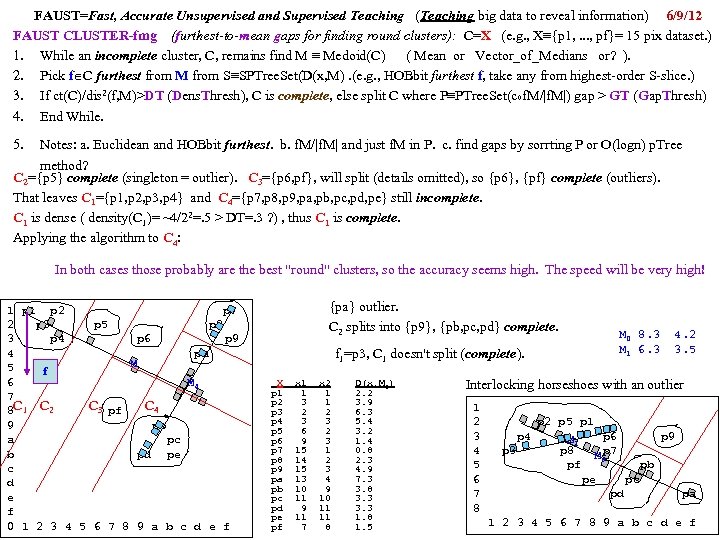FAUST=Fast, Accurate Unsupervised and Supervised Teaching (Teaching big data to reveal information) 6/9/12 FAUST CLUSTER-fmg (furthest-to-mean gaps for finding round clusters): C=X (e. g. , X≡{p 1, . . . , pf}= 15 pix dataset. ) 1. While an incomplete cluster, C, remains find M ≡ Medoid(C) ( Mean or Vector_of_Medians or? ). 2. Pick f C furthest from M from S≡SPTree. Set(D(x, M). (e. g. , HOBbit furthest f, take any from highest-order S-slice. ) 3. If ct(C)/dis 2(f, M)>DT (Dens. Thresh), C is complete, else split C where P≡PTree. Set(cof. M/|f. M|) gap > GT (Gap. Thresh) 4. End While. 5. Notes: a. Euclidean and HOBbit furthest. b. f. M/|f. M| and just f. M in P. c. find gaps by sorrting P or O(logn) p. Tree method? C 2={p 5} complete (singleton = outlier). C 3={p 6, pf}, will split (details omitted), so {p 6}, {pf} complete (outliers). That leaves C 1={p 1, p 2, p 3, p 4} and C 4={p 7, p 8, p 9, pa, pb, pc, pd, pe} still incomplete. C 1 is dense ( density(C 1)= ~4/22=. 5 > DT=. 3 ? ) , thus C 1 is complete. Applying the algorithm to C 4: In both cases those probably are the best "round" clusters, so the accuracy seems high. The speed will be very high! 1 p 2 p 7 2 p 3 p 5 p 8 3 p 4 p 6 p 9 4 pa 5 M f 6 M 4 7 C 1 C 2 C 3 C 4 8 pf 9 pb a pc b pd pe c d e f 0 1 2 3 4 5 6 7 8 9 a b c d e f {pa} outlier. C 2 splits into {p 9}, {pb, pc, pd} complete. f 1=p 3, C 1 doesn't split (complete). X x 1 x 2 p 1 1 1 p 2 3 1 p 3 2 2 p 4 3 3 p 5 6 2 p 6 9 3 p 7 15 1 p 8 14 2 p 9 15 3 pa 13 4 pb 10 9 pc 11 10 pd 9 11 pe 11 11 pf 7 8 D(x, M 0) 2. 2 3. 9 6. 3 5. 4 3. 2 1. 4 0. 8 2. 3 4. 9 7. 3 3. 8 3. 3 1. 8 1. 5 M 0 8. 3 4. 2 M 1 6. 3 3. 5 Interlocking horseshoes with an outlier 1 2 p 2 p 5 p 1 3 p 4 p 6 p 9 M 1 4 p 3 p 8 p 7 M 0 5 pf pb 6 pe pc 7 pd pa 8 1 2 3 4 5 6 7 8 9 a b c d e f
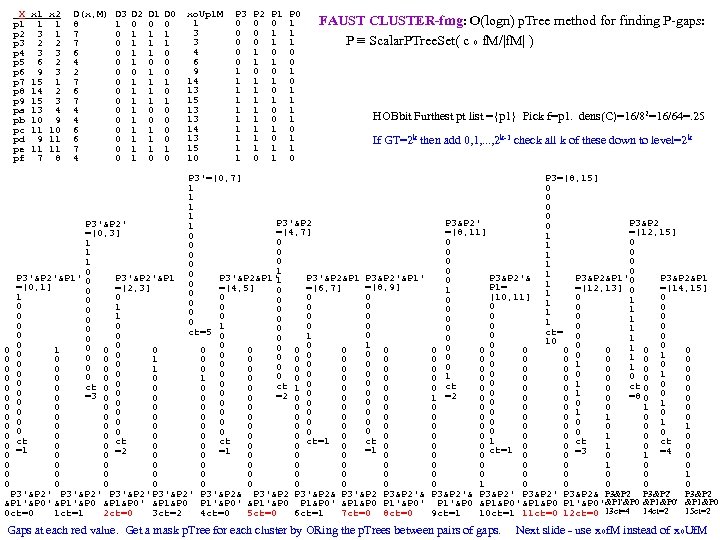X x 1 x 2 p 1 1 1 p 2 3 1 p 3 2 2 p 4 3 3 p 5 6 2 p 6 9 3 p 7 15 1 p 8 14 2 p 9 15 3 pa 13 4 pb 10 9 pc 11 10 pd 9 11 pe 11 11 pf 7 8 D(x, M) 8 7 7 6 4 2 7 6 7 4 4 6 6 7 4 D 3 1 0 0 0 0 D 2 0 1 1 1 1 D 1 0 1 1 1 1 0 0 1 1 1 0 D 0 0 1 1 0 0 0 1 0 xo. Up 1 M 1 3 3 4 6 9 14 13 15 13 13 14 13 15 10 P 3 0 0 0 1 1 1 1 1 P 2 0 0 0 1 1 1 1 1 0 P 1 0 1 0 1 0 0 1 1 P 0 1 1 1 0 0 1 1 1 1 0 FAUST CLUSTER-fmg: O(logn) p. Tree method for finding P-gaps: P ≡ Scalar. PTree. Set( c o f. M/|f. M| ) HOBbit Furthest pt list ={p 1} Pick f=p 1. dens(C)=16/82=16/64=. 25 If GT=2 k then add 0, 1, . . . , 2 k-1 check all k of these down to level=2 k P 3'=[0, 7] 1 1 P 3'&P 2' 1 =[4, 7] =[0, 3] 0 0 1 0 0 P 3'&P 2'&P 1' 0 P 3'&P 2'&P 1 P 3'&P 2&P 1' P 3'&P 2&P 1 P 3&P 2'&P 1' 1 0 =[0, 1] =[8, 9] =[2, 3] =[4, 5] =[6, 7] 0 0 0 1 0 0 0 0 1 0 0 0 ct=5 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 ct 1 0 ct 0 0 0 0 =2 0 0 =3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ct 0 0 0 0 0 ct ct ct=1 0 0 0 0 =1 0 =2 =1 0 0 0 0 0 0 0 0 0 P 3'&P 2' P 3'&P 2& P 3'&P 2 P 3&P 2'& &P 1'&P 0' &P 1'&P 0 &P 1&P 0' &P 1&P 0 P 1'&P 0' &P 1'&P 0 P 1&P 0' &P 1&P 0 P 1'&P 0' 0 ct=0 1 ct=1 2 ct=0 3 ct=2 4 ct=0 5 ct=0 6 ct=1 7 ct=0 8 ct=0 P 3=[8, 15] 0 0 P 3&P 2' P 3&P 2 0 =[8, 11] =[12, 15] 1 0 0 1 P 3&P 2'& P 3&P 2&P 1'0 P 3&P 2&P 1 0 1 P 1= =[12, 13] 0 =[14, 15] 1 [10, 11] 1 0 0 0 1 1 0 0 1 ct= 0 0 1 10 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 ct 0 0 0 0 1 0 0 =8 0 0 1 =2 0 0 1 0 0 0 0 0 1 1 0 0 0 1 0 0 0 ct=1 0 0 ct 1 0 ct 0 0 0 =3 0 1 =4 0 0 0 1 0 0 0 P 3&P 2'& P 3&P 2' P 3&P 2& P 3&P 2' P 3&P 2 P 1'&P 0 &P 1&P 0' &P 1&P 0 P 1'&P 0'&P 1'&P 0 &P 1&P 0' &P 1&P 0 15 ct=2 9 ct=1 10 ct=1 11 ct=0 12 ct=0 13 ct=4 14 ct=2 Gaps at each red value. Get a mask p. Tree for each cluster by ORing the p. Trees between pairs of gaps. Next slide - use xof. M instead of xo. Uf. M
FAUST CLUSTER ffd summary If DT=1. 1 then{pa} joins {p 7, p 8, p 9}. If DT=0. 5 then also {pf} joins {pb, pc. pd, pe} and {p 5} joins {p 1, p 2, p 3, p 4}. We call the overall method FAUST CLUSTER because it resembles FAUST CLASSIFY algorithmically and k (# of clusters) is dynamically determined. Improvements? Better stop condition? Is fmg better than ffd? In ffd, what if k over shoots its' optimal value? Add a fusion step each round? As Mark points out, having k too large can be problematic? . The proper definition of outlier or anomaly is a huge question. An outlier or anomaly should be a cluster that is both small and remote. How small? How remote? What combination? Should the definition be global or local? We need to research this (give users options and advice for their use). Md: create f=furthest pt from M, d(f, M) while creating D=SPTree. Set(d(x, M)? Or as a separate procedure, start with P=Dh (h=High Bit Pos. ) then recursively Pk<-- P & Dh-k until Pk+1=0. Then back up to Pk and take any of those points as f and that bit pattern is d(f, M). Note that this doesn't necessarily give the furthest pt from M but gives a pt sufficiently far from M. Or use HOBbit dis? Modify to get absolute furthest pt by jumping (when AND gives zero) to Pk+2 and continuing AND from there. (Dh gives a decent f (at furthest HOBbit dis). 1 p 2 p 7 2 p 3 p 5 p 8 3 p 4 p 6 p 9 4 pa 5 6 7 8 pf 9 pb a pc b pd pe c d e centriod=mean; h=1; DT= 1. 5 gives f 4 outliers and 3 non-outlier clusters 0 1 2 3 4 5 6 7 8 9 a b c d e f
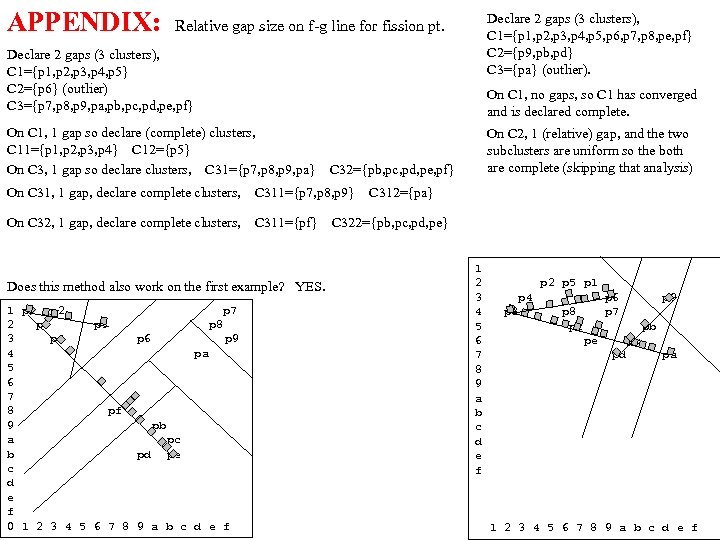APPENDIX: Relative gap size on f-g line for fission pt. Declare 2 gaps (3 clusters), C 1={p 1, p 2, p 3, p 4, p 5} C 2={p 6} (outlier) C 3={p 7, p 8, p 9, pa, pb, pc, pd, pe, pf} On C 1, 1 gap so declare (complete) clusters, C 11={p 1, p 2, p 3, p 4} C 12={p 5} On C 3, 1 gap so declare clusters, C 31={p 7, p 8, p 9, pa} C 32={pb, pc, pd, pe, pf} Declare 2 gaps (3 clusters), C 1={p 1, p 2, p 3, p 4, p 5, p 6, p 7, p 8, pe, pf} C 2={p 9, pb, pd} C 3={pa} (outlier). On C 1, no gaps, so C 1 has converged and is declared complete. On C 2, 1 (relative) gap, and the two subclusters are uniform so the both are complete (skipping that analysis) On C 31, 1 gap, declare complete clusters, C 311={p 7, p 8, p 9} C 312={pa} On C 32, 1 gap, declare complete clusters, C 311={pf} C 322={pb, pc, pd, pe} Does this method also work on the first example? YES. 1 p 2 p 7 2 p 3 p 5 p 8 3 p 4 p 6 p 9 4 pa 5 6 7 8 pf 9 pb a pc b pd pe c d e f 0 1 2 3 4 5 6 7 8 9 a b c d e f 1 2 p 2 p 5 p 1 3 p 4 p 6 p 9 4 p 3 p 8 p 7 5 pf pb 6 pe pc 7 pd pa 8 9 a b c d e f 1 2 3 4 5 6 7 8 9 a b c d e f
X p 1 p 2 p 3 p 4 p 5 p 6 p 7 p 8 p 9 pa pb pc pd pe pf x 1 8 5 2 3 6 9 9 6 13 13 12 11 10 8 7 max dis dis x 2 to M 0 f=p 3 g=pa PC 1 2 6. 32 7. 07 1 2 3. 60 9. 43 1 4 6. 13 0. 00 11. 4 1 3 1. 41 10. 7 1 2 4. 47 8. 60 1 3 7. 07 5. 65 0 4 7. 00 5. 00 0 4 4. 00 7. 61 1 3 11. 0 4. 00 0 7 11. 4 0. 00 0 5 10. 0 2. 23 0 6 9. 21 2. 23 0 7 8. 54 3. 00 0 6 6. 32 5. 09 0 5 5. 09 6. 32 1 dis dis to to to f 2=3 x 2 PC 222 M 1 2. 94 6. 32 2 1. 17 3. 61 2 3. 39 0. 00 4 2. 29 1. 41 3 1. 34 4. 47 2 3 4 1. 11 4. 00 4 0 3 7 1 1. 70 5 0 6 1 0. 75 7 1 1. 37 6 2. 52 5. 10 5 dis to M 1 2. 94 1. 17 3. 39 2. 29 1. 34 dis to M 2 dis f 2=6 dis g 2=a dis dis to dis PC 21 M 21 f 21=e g 21=6 PC 211 M 22 f 22=9 g 22=d PC 221 FAUST CLUSTER ffd on the "Linked Horseshoe" type example: 4. 24 3. 65 0. 00 1. 00 5. 65 5. 00 1 1 2. 98 1. 42 0. 86 1. 15 2. 42 4. 14 4. 00 5. 65 3. 60 4. 12 3. 16 4. 00 0. 00 2. 23 3. 00 5. 09 0 0 0 1 4. 24 3. 16 3. 65 2. 24 0. 00 0 1. 11 2. 52 PC 11 0 0 1 1 0 0 0 6. 02 2. 86 1. 84 0. 63 0. 89 4. 14 0. 00 Discuss: Here, DT=. 99 dis (DT=1. 5 all singeltons? ). to f 12=f PC 12 We expected FAUST to 3. 16 0 fail to find interlocked 3. 61 0 horseshoes, but hoped. e, g, pa and p 9 would be only singleton! 1. 08 3. 16 0 Can modify so it doesn't make almost everything outliers (singles, doubles 1. 08 1. 41 1 a. look at upper cluster bbdry (margin width)? b. use std ratio bddys? c. other? d. use a fussion step to weld the horseshoes back Next slide: gaps on f-g 2. 09 0. 00 1 line for fission pt. dis to M 12 1. 89 1. 72 0. 00 4. 00 2. 24 3. 61 5. 00 3. 00 2. 83 1. 41 0. 00 1 0 0 3. 16 1 1 2 p 2 p 5 p 1 3 p 4 p 6 p 9 4 p 3 p 8 p 7 5 pf pb 6 pe pc 7 pd pa 8 M 0 8. 1 4. 2 dens(C 0)= 15/6. 132
K-means: Assign each pt to closest mean and increment sum, count for mean recalculation (1 scan). Iterate until stop_cond. p. K-means: Same as above, but both assignment and means recalculation are done without scanning: 1. Pick K centroids, {Ci}i=1. . K 2. Calc SPTree. Set, Di=D(X, Ci) (col of distances from all x to Ci) to get P(Di Dj) i
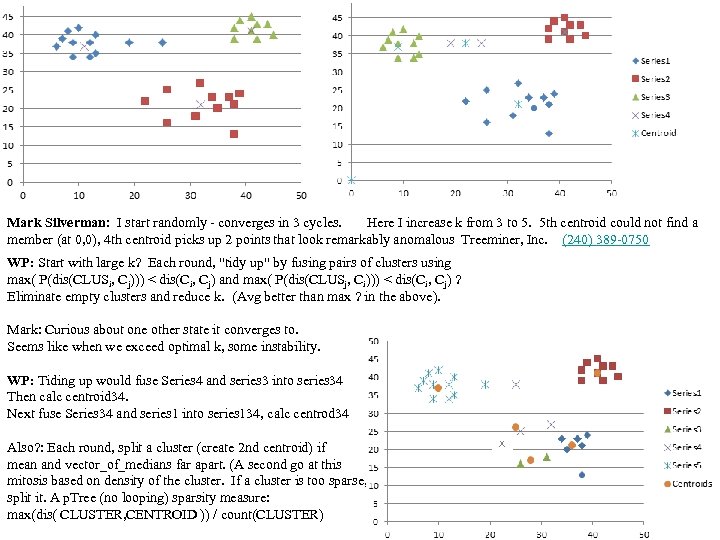Mark Silverman: I start randomly - converges in 3 cycles. Here I increase k from 3 to 5. 5 th centroid could not find a member (at 0, 0), 4 th centroid picks up 2 points that look remarkably anomalous Treeminer, Inc. (240) 389 -0750 WP: Start with large k? Each round, "tidy up" by fusing pairs of clusters using max( P(dis(CLUSi, Cj))) < dis(Ci, Cj) and max( P(dis(CLUSj, Ci))) < dis(Ci, Cj) ? Eliminate empty clusters and reduce k. (Avg better than max ? in the above). Mark: Curious about one other state it converges to. Seems like when we exceed optimal k, some instability. WP: Tiding up would fuse Series 4 and series 3 into series 34 Then calc centroid 34. Next fuse Series 34 and series 1 into series 134, calc centrod 34 Also? : Each round, split a cluster (create 2 nd centroid) if mean and vector_of_medians far apart. (A second go at this mitosis based on density of the cluster. If a cluster is too sparse, split it. A p. Tree (no looping) sparsity measure: max(dis( CLUSTER, CENTROID )) / count(CLUSTER) X
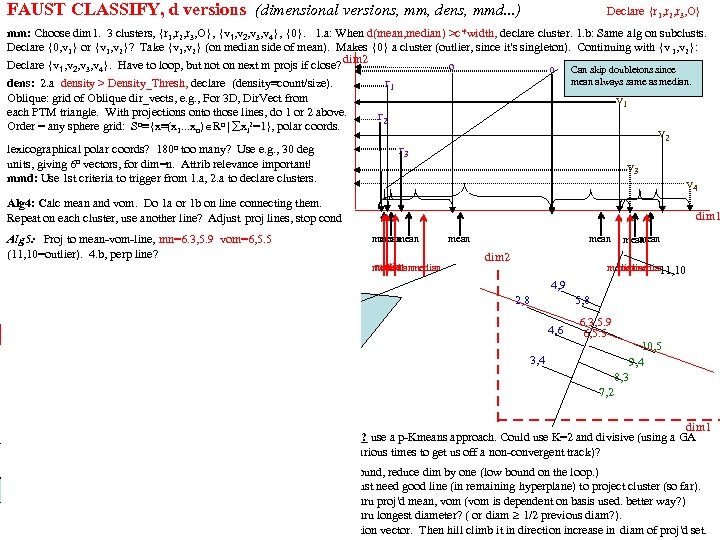FAUST CLASSIFY, d versions (dimensional versions, mm, dens, mmd. . . ) Declare {r 1, r 2, r 3, O} mm: Choose dim 1. 3 clusters, {r 1, r 2, r 3, O}, {v 1, v 2, v 3, v 4}, {0}. 1. a: When d(mean, median) >c*width, declare cluster. 1. b: Same alg on subclusts. Declare {0, v 1} or {v 1, v 2}? Take {v 1, v 2} (on median side of mean). Makes {0} a cluster (outlier, since it's singleton). Continuing with {v 1, v 2}: Declare {v 1, v 2, v 3, v 4}. Have to loop, but not on next m projs if close? dim 2 o 0 Can skip doubletons since mean always same as median. r 1 dens: 2. a density > Density_Thresh, declare (density≡count/size). Oblique: grid of Oblique dir_vects, e. g. , For 3 D, Dir. Vect from v 1 each PTM triangle. With projections onto those lines, do 1 or 2 above. r 2 Order = any sphere grid: Sn≡{x≡(x 1. . . xn) Rn | xi 2=1}, polar coords. lexicographical polar coords? 180 n too many? Use e. g. , 30 deg units, giving 6 n vectors, for dim=n. Attrib relevance important! mmd: Use 1 st criteria to trigger from 1. a, 2. a to declare clusters. v 2 r 3 v 4 Alg 4: Calc mean and vom. Do 1 a or 1 b on line connecting them. Repeat on each cluster, use another line? Adjust proj lines, stop cond Alg 5: Proj to mean-vom-line, mn=6. 3, 5. 9 vom=6, 5. 5 (11, 10=outlier). 4. b, perp line? mean median 3 vom=(7, 4, 3) dim 1 mean=(8. 18, 3. 27, 3. 73) mean dim 2 mean median 11, 10 4, 9 2, 8 5, 8 6. 3, 5. 9 4, 6 6, 5. 5 10, 5 3, 4 9, 4 8, 3 7, 2 435 524 504 924 545 323 b 43 e 43 1 c 63 752 dim 1 Other option? use a p-Kmeans approach. Could use K=2 and divisive (using a GA f 72 mutation at various times to get us off a non-convergent track)? 21. no clusters determined yet. 2. (9, 2, 4) determined as an outlier cluster. 3. Use red dim line, (7, 5, 2) an outlier cluster. maroon pts determined as cluster, purple pts too. 3. a use mean-vom again would the same be determined? Notes: Each round, reduce dim by one (low bound on the loop. ) Each round, just need good line (in remaining hyperplane) to project cluster (so far). 1. pick line thru proj'd mean, vom (vom is dependent on basis used. better way? ) 2. pick line thru longest diameter? ( or diam 1/2 previous diam? ). 3. try a direction vector. Then hill climb it in direction increase in diam of proj'd set.
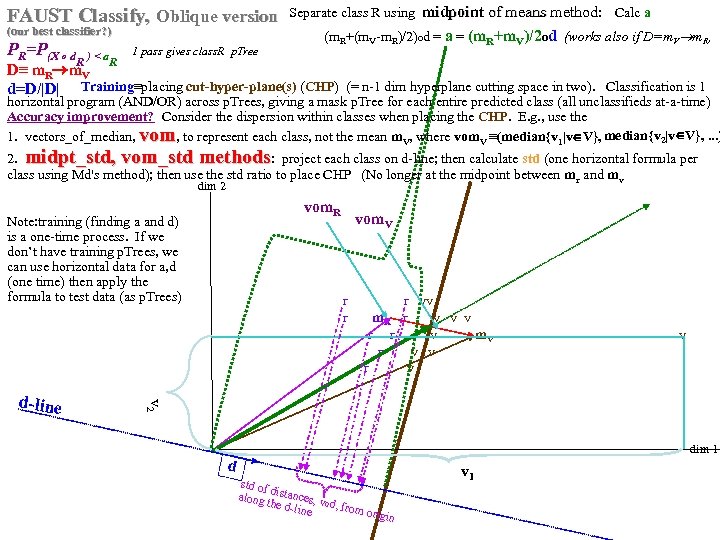FAUST Classify, Oblique version (our best classifier? ) PR=P(X o d ) < a 1 pass gives class. R p. Tree R R Separate class R using midpoint of means method: Calc a of means (m. R+(m. V-m. R)/2)od = a = (m. R+m. V)/2 od (works also if D=m. V m. R, D≡ m. R m. V Training≡placing cut-hyper-plane(s) (CHP) (= n-1 dim hyperplane cutting space in two). Classification is 1 d=D/|D| horizontal program (AND/OR) across p. Trees, giving a mask p. Tree for each entire predicted class (all unclassifieds at-a-time) Accuracy improvement? Consider the dispersion within classes when placing the CHP. E. g. , use the 1. vectors_of_median, vom, to represent each class, not the mean m. V, where vom. V ≡(median{v 1|v V}, median{v 2|v V}, . . . ) 2. midpt_std, vom_std methods: project each class on d-line; then calculate std (one horizontal formula per class using Md's method); then use the std ratio to place CHP (No longer at the midpoint between mr and mv dim 2 vom. R Note: training (finding a and d) is a one-time process. If we don’t have training p. Trees, we can use horizontal data for a, d (one time) then apply the formula to test data (as p. Trees) r vv r m. R r v v v r r v m. V v r v v 2 d-line vom. V dim 1 d std of along distances, v the do line d, from ori gin v 1
What ordering is best for spherical data (e. g. , Data sets involving astronomical bodies on the celestial sphere, which shares its' origin and equatorial plane with the earth, but has no radius. Hierarchical Triangle Mesh (HTM) orders its' recursive equilateral triangulations as: PTree Triangular Mesh (PTM) ordering is: Peel from south to north pole along quadrant great circles and the equator. R Level-2 follows the level-1 LLRR pattern with another LLRR pattern. Level-3 follows level-2 with LR when level-2 pattern is L and RL when level-2 pattern is R 1, 1, 2 1. 1. 3 1, 1, 1 L L L 1, 1, 0 1 , 21, 3 1 R L PTM_LLRR_LR. . . HTM sub-triangle ordering L 1 , 0 1 , 1 equator L R L L R R R R L R R R L L R L R R R L R R R L R R L south pole L . . . R RL Theorem: n, an n-sphere filling (n-1)-sphere? R L R Corollary: sphere filling circle (2 -sphere filling 1 -sphere). d(x, C) ≡ lim d(x, Cn) lim sidelengthn sidelength 1 * lim ½n = 0 L L x L L L R sidelengthn+1 = ½ * sidelengthn. L R distance(x, Cn) sidelength (=diameter) of the level-n triangles. L R Proof of Corollary: Let Cn ≡ the level-n circle, C ≡ limitn Cn is a circle which fills the 2 -sphere! Proof: Let x be any point on the 2 -sphere. north pole
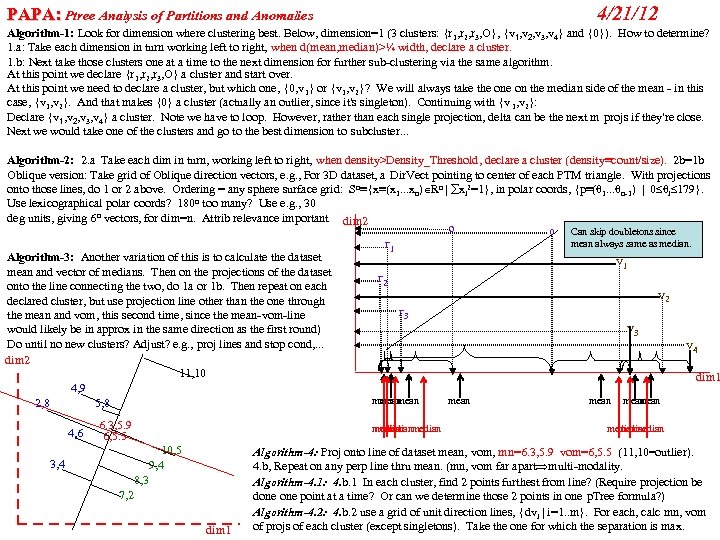PAPA: Ptree Analysis of Partitions and Anomalies 4/21/12 Algorithm-1: Look for dimension where clustering best. Below, dimension=1 (3 clusters: {r 1, r 2, r 3, O}, {v 1, v 2, v 3, v 4} and {0}). How to determine? 1. a: Take each dimension in turn working left to right, when d(mean, median)>¼ width, declare a cluster. 1. b: Next take those clusters one at a time to the next dimension for further sub-clustering via the same algorithm. At this point we declare {r 1, r 2, r 3, O} a cluster and start over. At this point we need to declare a cluster, but which one, {0, v 1} or {v 1, v 2}? We will always take the on the median side of the mean - in this case, {v 1, v 2}. And that makes {0} a cluster (actually an outlier, since it's singleton). Continuing with {v 1, v 2}: Declare {v 1, v 2, v 3, v 4} a cluster. Note we have to loop. However, rather than each single projection, delta can be the next m projs if they're close. Next we would take one of the clusters and go to the best dimension to subcluster. . . Algorithm-2: 2. a Take each dim in turn, working left to right, when density>Density_Threshold, declare a cluster (density≡count/size). 2 b=1 b Oblique version: Take grid of Oblique direction vectors, e. g. , For 3 D dataset, a Dir. Vect pointing to center of each PTM triangle. With projections onto those lines, do 1 or 2 above. Ordering = any sphere surface grid: S n≡{x≡(x 1. . . xn) Rn | xi 2=1}, in polar coords, {p≡(θ 1. . . θn-1) | 0 θi 179}. Use lexicographical polar coords? 180 n too many? Use e. g. , 30 deg units, giving 6 n vectors, for dim=n. Attrib relevance important dim 2 o 0 Can skip doubletons since mean always same as median. r 1 v 1 r 2 v 2 r 3 v 4 Algorithm-3: Another variation of this is to calculate the dataset mean and vector of medians. Then on the projections of the dataset onto the line connecting the two, do 1 a or 1 b. Then repeat on each declared cluster, but use projection line other than the one through the mean and vom, this second time, since the mean-vom-line would likely be in approx in the same direction as the first round) Do until no new clusters? Adjust? e. g. , proj lines and stop cond, . . . dim 2 11, 10 dim 1 4, 9 mean mean 2, 8 5, 8 6. 3, 5. 9 median median 4, 6 6, 5. 5 10, 5 Algorithm-4: Proj onto line of dataset mean, vom, mn=6. 3, 5. 9 vom=6, 5. 5 (11, 10=outlier). 3, 4 9, 4 4. b, Repeat on any perp line thru mean. (mn, vom far apart multi-modality. 8, 3 Algorithm-4. 1: 4. b. 1 In each cluster, find 2 points furthest from line? (Require projection be 7, 2 done point at a time? Or can we determine those 2 points in one p. Tree formula? ) Algorithm-4. 2: 4. b. 2 use a grid of unit direction lines, {dvi | i=1. . m}. For each, calc mn, vom of projs of each cluster (except singletons). Take the one for which the separation is max. dim 1
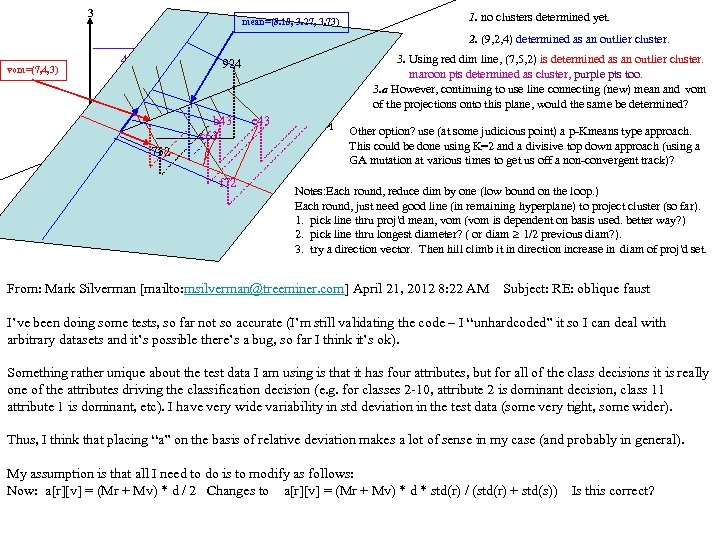3 mean=(8. 18, 3. 27, 3. 73) 1. no clusters determined yet. 2. (9, 2, 4) determined as an outlier cluster. vom=(7, 4, 3) 2 3. Using red dim line, (7, 5, 2) is determined as an outlier cluster. 435 524 504 924 maroon pts determined as cluster, purple pts too. 545 3. a However, continuing to use line connecting (new) mean and vom 323 of the projections onto this plane, would the same be determined? b 43 e 43 1 Other option? use (at some judicious point) a p-Kmeans type approach. c 63 This could be done using K=2 and a divisive top down approach (using a 752 GA mutation at various times to get us off a non-convergent track)? f 72 Notes: Each round, reduce dim by one (low bound on the loop. ) Each round, just need good line (in remaining hyperplane) to project cluster (so far). 1. pick line thru proj'd mean, vom (vom is dependent on basis used. better way? ) 2. pick line thru longest diameter? ( or diam 1/2 previous diam? ). 3. try a direction vector. Then hill climb it in direction increase in diam of proj'd set. From: Mark Silverman [mailto: msilverman@treeminer. com] April 21, 2012 8: 22 AM Subject: RE: oblique faust I’ve been doing some tests, so far not so accurate (I’m still validating the code – I “unhardcoded” it so I can deal with arbitrary datasets and it’s possible there’s a bug, so far I think it’s ok). Something rather unique about the test data I am using is that it has four attributes, but for all of the class decisions it is really one of the attributes driving the classification decision (e. g. for classes 2 -10, attribute 2 is dominant decision, class 11 attribute 1 is dominant, etc). I have very wide variability in std deviation in the test data (some very tight, some wider). Thus, I think that placing “a” on the basis of relative deviation makes a lot of sense in my case (and probably in general). My assumption is that all I need to do is to modify as follows: Now: a[r][v] = (Mr + Mv) * d / 2 Changes to a[r][v] = (Mr + Mv) * d * std(r) / (std(r) + std(s)) Is this correct?
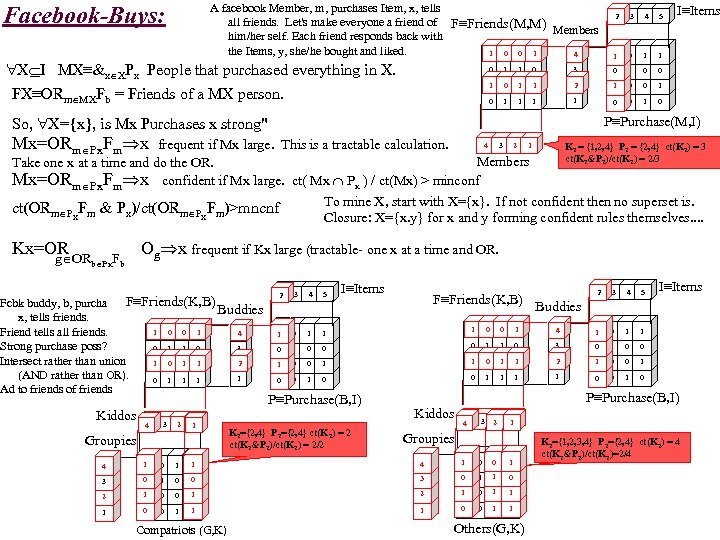A facebook Member, m, purchases Item, x, tells all friends. Let's make everyone a friend of F≡Friends(M, M) Members him/her self. Each friend responds back with the Items, y, she/he bought and liked. 0 1 1 0 1 4 Facebook-Buys: X I MX≡&x XPx People that purchased everything in X. FX≡ORm MXFb = Friends of a MX person. 2 3 4 5 1 0 1 I≡Items 1 0 1 1 0 3 0 1 0 1 1 2 1 0 0 1 1 1 1 0 0 1 0 P≡Purchase(M, I) So, X={x}, is Mx Purchases x strong" Mx=ORm Px. Fm x frequent if Mx large. This is a tractable calculation. 4 3 2 K 2 = {1, 2, 4} P 2 = {2, 4} ct(K 2) = 3 ct(K 2&P 2)/ct(K 2) = 2/3 1 Members Take one x at a time and do the OR. Mx=ORm Px. Fm x confident if Mx large. ct( Mx Px ) / ct(Mx) > minconf To mine X, start with X={x}. If not confident then no superset is. ct(ORm Px. Fm & Px)/ct(ORm Px. Fm)>mncnf Closure: X={x. y} for x and y forming confident rules themselves. . Kx=OR Og x frequent if Kx large (tractable- one x at a time and OR. g ORb Px. Fb F≡Friends(K, B) Fcbk buddy, b, purchases Buddies x, tells friends. 0 1 1 0 1 4 Friend tells all friends. Strong purchase poss? 3 0 1 1 0 Intersect rather than union 1 0 1 1 2 (AND rather than OR). 1 0 1 1 1 Ad to friends of friends Kiddos 4 4 3 2 1 1 Groupies 44 1 1 0 1 4 5 I≡Items 2 3 4 5 4 1 0 3 0 1 0 0 1 2 1 0 0 1 1 1 0 0 1 0 3 1 0 1 1 1 0 1 0 0 0 1 1 1 F≡Friends(K, B) 1 0 0 P≡Purchase(B, I) K 2={2, 4} P 2={2, 4} ct(K 2) = 2 ct(K 2&P 2)/ct(K 2) = 2/2 Buddies P≡Purchase(B, I) Kiddos 4 4 3 2 2 1 1 Groupies 1 1 44 1 1 0 0 0 33 0 0 1 0 0 0 33 22 1 1 0 0 1 1 22 1 1 0 1 1 11 0 0 0 1 1 0 11 0 0 0 1 1 1 0 Compatriots (G, K) I≡Items 1 2 Others(G, K) K 2={1, 2, 3, 4} P 2={2, 4} ct(K 2) = 4 ct(K 2&P 2)/ct(K 2)=2/4
The Multi-hop Closure Theorem A hop is a relationship, R, hopping from entities E to F. U(H, I) upward closure: If a condition is true of A then it is true of all supersets D of A. S(F, G) 0 0 0 1 1 3 4 5 0 0 1 0 0 0 1 1 0 1 4 3 2 1 I C H G 1 1 0 1 For transitive (a+c)-hop strong rule mine where the focus or count entity is a hops from the antecedent and c hops from the consequent, if a (or c) is odd/even then downward/upward closure applies to frequency (confidence). 1 0 2 downward closure: If a condition is true of A, then it is true for all subsets D of A. 1 1 0 1 0 0 0 1 1 2 3 4 5 0 0 0 0 1 4 3 2 1 T(G, H) F 4 3 2 1 E A Odd downward Even upward R(E, F) The proof of theorem: a p. Tree, X, is said to be "covered by" a p. Tree, Y, if 1 -bit in X, there is a 1 -bit at that same position in Y. Lemma-0: For any two p. Trees, X and Y, X & Y is covered by X and ct(X) ct(X&Y) Proof-0: ANDing with Y may zero some of X's 1 -positions but never ones any of X's 0 -positions. Lemma-1: Let A B, &a BXa is covered by &a AXa Proof-1: Let Z=&a B-AXa then &a B Xa = Z & (&a A Xa), so the result follows from lemma-0. Lemma-2: For a (or c) =0, frequency and confidence are upward closed Proof-2: ct(B) ct(A), so ct(A)>mnsp ct(B)>mnsp and ct(C&A)/ct(C)>mncf ct(C&B)/ct(C)>. mncf Lemma-3: If a (or c) we have upward/downward closure of frequency or confidence, then for a+1 (or c+1) we have downward/upward closer. Proof-3: Taking the a and upward closure, going to a+1 and D A, we are removing ANDs in the numerator for both frequency and confidence, so by Lemma-1, the a+1 numerator is covers the a numerator and therefore the a+1_count the a_count. Therefore, the condition (frequency or confidence) holds in the a+1 case and we have downward closure.
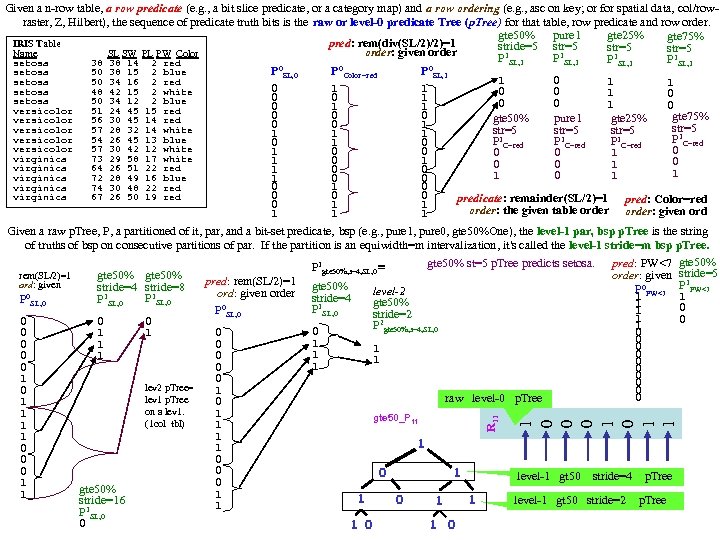1 0 0 0 1 1 R 11 Given a n-row table, a row predicate (e. g. , a bit slice predicate, or a category map) and a row ordering (e. g. , asc on key; or for spatial data, col/rowraster, Z, Hilbert), the sequence of predicate truth bits is the raw or level-0 predicate Tree (p. Tree) for that table, row predicate and row order. gte 50% pure 1 gte 25% gte 75% pred: rem(div(SL/2)/2)=1 IRIS Table stride=5 str=5 order: given order Name SL SW PL PW Color P 1 SL, 1 setosa 38 38 14 2 red 0 0 0 P SL, 0 P Color=red P SL, 1 setosa 50 38 15 2 blue 1 0 1 setosa 50 34 16 2 red 1 0 1 1 setosa 48 42 15 2 white 0 0 1 0 0 0 1 setosa 50 34 12 2 blue 0 0 1 1 versicolor 51 24 45 15 red 0 0 0 gte 75% gte 50% pure 1 gte 25% versicolor 56 30 45 14 red 0 0 1 str=5 versicolor 57 28 32 14 white str=5 1 1 1 versicolor 54 26 45 13 blue P 1 C=red P C=red 0 1 0 versicolor 57 30 42 12 white 0 1 0 0 1 virginica 73 29 58 17 white 1 0 0 0 1 virginica 64 26 51 22 red 1 0 0 1 1 0 1 virginica 72 28 49 16 blue 1 0 0 0 1 0 virginica 74 30 48 22 red 0 0 0 virginica 67 26 50 19 red predicate: remainder(SL/2)=1 pred: Color=red 0 1 1 order: the given table order: given ord 1 1 1 Given a raw p. Tree, P, a partitioned of it, par, and a bit-set predicate, bsp (e. g. , pure 1, pure 0, gte 50%One), the level-1 par, bsp p. Tree is the string of truths of bsp on consecutive partitions of par. If the partition is an equiwidth=m intervalization, it's called the level-1 stride=m bsp p. Tree. gte 50% st=5 p. Tree predicts setosa. pred: PW<7 gte 50% P 1 gte 50%, s=4, SL, 0 ≡ order: given stride=5 rem(SL/2)=1 gte 50% 1 pred: rem(SL/2)=1 gte 50% ord: given stride=4 stride=8 P 0 PW<7 P PW<7 level-2 ord: given order stride=4 1 1 0 1 1 P SL, 0 gte 50% 1 0 P 1 SL, 0 P 0 SL, 0 1 stride=2 1 0 0 P 2 gte 50%, s=4, SL, 0 1 0 1 0 1 0 1 0 0 0 1 0 lev 2 p. Tree= 0 1 0 0 raw level-0 p. Tree lev 1 p. Tree 0 1 on a lev 1. 1 1 gte 50_P 11 (1 col tbl) 1 1 1 0 0 0 1 level-1 gt 50 stride=4 p. Tree 0 1 gte 50% 1 1 1 0 level-1 gt 50 stride=2 p. Tree 1 stride=16 1 1 P 1 SL, 0 0 1 0 1 1
FAUST Satlog evaluation R G ir 1 ir 2 mn 62. 83 95. 29 108. 12 89. 50 1 48. 84 39. 91 113. 89 118. 31 2 87. 48 105. 50 110. 60 87. 46 3 77. 41 90. 94 95. 61 75. 35 4 59. 59 62. 27 83. 02 69. 95 5 69. 01 77. 42 81. 59 64. 13 7 R G ir 1 ir 2 std 8 15 13 9 1 8 13 13 19 2 5 7 7 6 3 6 8 8 7 4 6 12 13 13 5 5 8 9 7 7 2 pstdr a = pmr + (pmv-pmr) = pstd +2 pstd v r pmr*pstdv + pmv*2 pstdr +2 pstdv Non. Oblique lev-0 1's 2's 3's 4's 5's 7's True Positives: 99 193 325 130 151 257 Class actual-> 461 224 397 211 237 470 2 s 1 Non. Oblq lev 1 gt 50 1's 2's 3's 4's 5's 7's , # of FPs reduced and TPs somewhat reduced. Better? Parameterize the 2 to max TPs, min FPs. Best parameter? True Positives: 212 183 314 103 157 330 False Positives: 14 1 42 103 36 189 Oblique level-0 using midpoint of means 1 2 3 4 5 7 tot 1's 2's 3's 4's 5's 7's 461 224 397 211 237 470 2000 TP actual True Positives: 322 199 344 145 174 353 False Positives: 28 3 80 171 107 74 99 193 325 130 151 257 1155 TP non. Ob L 0 pure 1 Oblique level-0 using means and stds of projections (w/o cls elim) 1's 2's 3's 4's 5's 7's 212 183 314 103 157 330 1037 TP non. Oblique True Positives: 359 205 332 144 175 324 14 1 42 103 36 189 385 FP level-1 50% False Positives: 29 18 47 156 131 58 322 199 344 145 174 353 1537 TP Obl level-0 Oblique lev-0, means, stds of projections (w cls elim in 2345671 order) Note that none occurs 28 3 80 171 107 74 463 FP Means. Mid. Point 1's 2's 3's 4's 5's 7's True Positives: 359 205 332 144 175 324 359 205 332 144 175 324 1539 TP Obl level-0 False Positives: 29 18 47 156 131 58 29 18 47 156 131 58 439 FP s 1/(s 1+s 2) Oblique level-0 using means and stds of projections, doubling pstd No elimination! 410 212 277 179 199 324 1601 TP 2 s 1/(2 s 1+s 2) 1's 2's 3's 4's 5's 7's 114 40 113 259 235 58 819 FP Ob L 0 no elim True Positives: 410 212 277 179 199 324 False Positives: 114 40 113 259 235 58 309 212 277 154 163 248 1363 TP 2 s 1/(2 s 1+s 2) Oblique lev-0, means, stds of projs, doubling pstdr, classify, eliminate in 2, 3, 4, 5, 7, 1 ord 22 40 65 211 196 27 561 FP Ob L 0 234571 1's 2's 3's 4's 5's 7's True Positives: 309 212 277 154 163 248 329 189 277 154 164 307 1420 TP 2 s 1/(2 s 1+s 2) False Positives: 22 40 65 211 196 27 25 1 113 211 121 33 504 FP Ob L 0 347512 Oblique lev-0, means, stds of projs, doubling pstdr, classify, elim 3, 4, 7, 5, 1, 2 ord 355 189 277 154 164 307 1446 TP 2 s 1/(2 s 1+s 2) 1's 2's 3's 4's 5's 7's 37 18 14 259 121 33 482 FP Ob L 0 425713 True Positives: 329 189 277 154 164 307 False Positives: 25 1 113 211 121 33 2 33 56 58 6 18 173 TP Band. Class rule 0 0 24 46 0 193 263 FP mining (below) 2 s 1/(2 s 1+s 2) elim ord: 425713 TP: 355 205 224 179 172 307 FP: 37 18 14 259 121 33 G[0, 46] 2 G[47, 64] 5 Conclusion? Means. Mid. Point and G[65, 81] 7 G[81, 94] 4 red green ir 1 ir 2 Oblique std 1/(std 1+std 2) abv below abv below avg G[94, 255] {1, 3} are best with the Oblique 1 4. 33 2. 10 5. 29 2. 16 1. 68 8. 09 13. 11 0. 94 4. 71 2 1. 30 1. 12 6. 07 0. 94 2. 36 version slightly better. R[0, 48] {1, 2} 3 1. 09 2. 16 8. 09 6. 07 1. 07 13. 11 5. 27 I wonder how these two methods R[49, 62] {1, 5} 4 1. 31 1. 09 1. 18 5. 29 1. 67 1. 68 3. 70 1. 07 2. 12 5 1. 30 4. 33 1. 12 1. 32 15. 37 1. 67 3. 43 3. 70 4. 03 would work on Netflix? R[82, 255] 3 7 2. 10 1. 31 1. 32 1. 18 15. 37 3. 43 4. 12 Two ways: ir 1[0, 88] {5, 7} ir 2[0, 52] 5 cls avg above=(std+stdup)/gap 4 2. 12 below=(std+stddn)/gapdn 2 2. 36 UTbl(User, M 1, . . . , M 17, 770) (u, m); um. Training. Tbl = Sub. UTbl(Support(m), Support(u), m) 5 4. 03 suggest ord 425713 7 4. 12 1 4. 71 MTbl(Movie, U 1, . . . , U 480189) (m, u); mu. Training. Tbl = Sub. MTbl(Support(u), Support(m), u) 3 5. 27
User. Table(u. ID, m 1, . . . , m 17770) u. ID rating date u i 1 rmk, u dmk, u ui 2 . . . ui n k m. ID u. ID rating date m 1 u 1 rm, u dm, u m 1 u 2 . . . m 17770 u 480189 r 17770, 480189 d 17770, 480189 or U 2649429 MTbl(m. ID, u 1. . . u 480189) u 1 uk u 480189 m 1 rm rmhuk . 1/0 . 1 2 4 324513? 45 5 5 . u . 1 2 4 324513? 45 5 5 huk . m 17770 . 47 B u 480189 MPTree. Set 3*480189 bitslices wide u 0, 2 u 480189, 0 m 1 47 B u 480189 47 B (u, m) to be predicted, form um. Training. Tbl=Sub. UTbl(Support(m), Support(u), m) : m h : : uk u : m h : m 0, 2 . m 17769, 0 m u 1 : uk Main: (m, u, r, d) avg: 209 m/u ---- 100, 480, 507 ---- mk(u, r, d) avg: 5655 u/m UPTree. Set 3*17770 bitslices wide m 1 . . . mh . . . m 17770 m u 1 Netflix data {mk}k=1. . 17770 Lots of 0 s in vector sp, um. Traning. Tbl). Want the largest subtable without zeros. How? 0/1 m 17770 Sub. UTbl( n Sup(u) m. Sup(n), Sup(u), m)? 47 B Of course, the two supports won't be tight together like that but they are put that way for clarity. (u, m) to be predicted, from um. Training. Tbl = Sub. UTbl(Support(m), Support(u), m) Using Coordinate-wise FAUST (not Oblique), in each coordinate, n Sup(u), divide up all users v Sup(n) Sup(m) into their rating classes, rating(m, v). then: 1. calculate the class means and stds. Sort means. 2. calculate gaps 3. choose best gap and define cutpoint using stds. Coord FAUST, in each coord, v Sup(m), divide up all movies n Sup(v) Sup(u) to rating classes 1. calculate the class means and stds. Sort means. 2. calculate gaps 3. choose best gap and define cutpoint using stds. This of course may be slow. How can we speed it up? Gaps alone not best (especially since the sum of the gaps is no more than 4 and there are 4 gaps). Weighting (correlation(m, n)-based) useful (higher the correlation the more significant the gap? ? ) Ctpts constructed for just this one prediction, rating(u, m). Make sense to find all of them. Should just find, e, g, which n-class-mean(s) rating(u, n) is closest to and make those the votes?
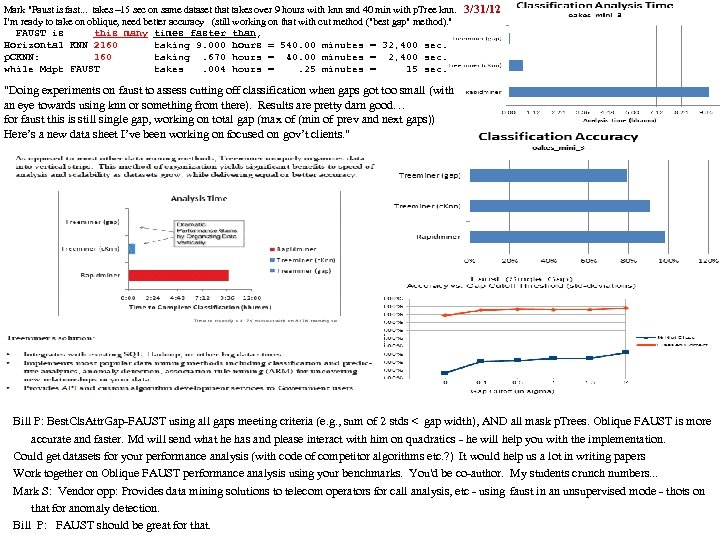Mark "Faust is fast. . . takes ~15 sec on same dataset that takes over 9 hours with knn and 40 min with p. Tree knn. 3/31/12 I’m ready to take on oblique, need better accuracy (still working on that with cut method ("best gap" method). " FAUST is this many times faster than, Horizontal KNN 2160 taking 9. 000 hours = 540. 00 minutes = 32, 400 sec. p. CKNN: 160 taking . 670 hours = 40. 00 minutes = 2, 400 sec. while Mdpt FAUST takes . 004 hours = . 25 minutes = 15 sec. "Doing experiments on faust to assess cutting off classification when gaps got too small (with an eye towards using knn or something from there). Results are pretty darn good… for faust this is still single gap, working on total gap (max of (min of prev and next gaps)) Here’s a new data sheet I’ve been working on focused on gov’t clients. " Bill P: Best. Cls. Attr. Gap-FAUST using all gaps meeting criteria (e. g. , sum of 2 stds < gap width), AND all mask p. Trees. Oblique FAUST is more accurate and faster. Md will send what he has and please interact with him on quadratics - he will help you with the implementation. Could get datasets for your performance analysis (with code of competitor algorithms etc. ? ) It would help us a lot in writing papers Work together on Oblique FAUST performance analysis using your benchmarks. You'd be co-author. My students crunch numbers. . . Mark S: Vendor opp: Provides data mining solutions to telecom operators for call analysis, etc - using faust in an unsupervised mode - thots on that for anomaly detection. Bill P: FAUST should be great for that.
kmurph 2@clemson. edu Mar 06 Yes, p. TREES for med informatics, Bill! We could work so many miracles. . data we can generate requires robust informatics, comp. bio. would put resources into this. Keith Murphy, Chair Genetics/ Biochem Dir, Clemson U Genomics Inst. WP: 3/6 Wave applied p. Trees to Bioinformatics too (took second in 2002 ACM KDD-cup in bioinformatics and took first in the 2006 ACM KDD-cup in medical informatics. 2006 ACM KDD Cup Winning Team Leader Task 3. http: //www. cs. unm. edu/kdd_cup_2006, http: //www. cs. unm. edu/files/kdd-cup-2006 -task-spec-final. pdf. 2002 ACM KDD Cup, Task 2. Yeast Gene Regulation Prediction: See http: //www. acm. org/sigs/sigkdd/kddcup/index. php? section=2002&method=res Mark Silverman Feb 29: tweaking Greg's faust impl and look at gap split (looks for max gap, not max gap on both side of mean -should be? ) WP: looks like 50%ones impure p. Trees can give cut-hyperplanes (for FAUST) as good as raw p. Trees. what's the advantage? Since FAUST training is a 1 -time process, it isn't speed critical. Very fast impure p. Tree batch classification (after training) would be very exciting. Once the cut-hyper-planes identified (e. g. , FPGA spits out 50%ones impure p. Trees for incoming unclassified datasets (e. g. , satellite images) and sends them thro (FPGA) for "Md's "One-Pass-Across-Columns = OPAC" batch classification - all happening on-the-fly with nearly zero delay. . . For PINE (nearest neighbor), we don't even train a model, so the 50%ones impure p. Tree classification-phase could be very significantly better. Business Intelligence= "What does this customer want next, based on histories? ": FAUST is model-based (training phase=build model of 1 hyperplane for Oblique or up to 1 -per-col for non-Oblique). Use the model to classify. In Bus-Intel, with every new unclassified sample, a different vector space appears. (every customer rates a different set of items). So to use FAUST-PINE, there's the non-vector-space problem to solve. non-Oblique FAUST better than Oblique, since cols have different cardinalities (not a vector space to calculate oblique hyperplanes). In general, we're attempting is to marry MYRRH multi-hop Relationship or Rule Mining with FAUST-PINE Classification or Table Mining. On Social Network Mining: We have some social network mining research threads percolating: 1. facebook-friends multi-hopped with buying-preference relationships (or multi-hopped with security threat relationships or with? ) 2. implications of twitter blooms for event prediction (e. g. , commod/stock changes, events, political trends, bubbles/bursts, purchasing patterns. . . I would like to tie image classification with social networks somehow too ; -) WP: 3/1/12 Note on ". . . very excited about the discussions on MYRRH and applying it to classification problems, seems hugely innovative. . . " I want to try to view Images as relationships, rather than as tables, each row = a pixel and each cols is "the photon count in a frequency band". Any table=relationship (AKA, a matrix, rolodex card) w 2 entity axes: 1. usual row entity (e. g. , pixels), 2. col entity(s) (e. g. , wavlen interval). Any matrix is a dual pair of tables (via rotation). Cust-Item Rating matrix is rating tbl pair: Custs(Items) and its rotated dual, Item(Custs). When sufficient #of fine-band, hyper-spectral sensors in the air (plus on/in the ground), there will be a sufficient # of separate columns to do MYRRH on the relationship between pixels and wavelengths multi-hopped with the relationship between classes and pixels (. . . nearly every measurement is a summarization or a intervalization (even a pixel is a 2 -D intervalization of an infinite set of points in space), so viewing wavelength as an intervalization of a continuous phenomenon is just as valid, right? ). What if we do FAUST-PINE on the rotated image relationship, Wavelength(pixel_photon_count) instead of, Pixel(Wavelength_photon_count)? Note that classes which are not convex in Pix(WL) (that are spread out spatially all over the image) might be convex in WL(Pix)? tried prelims - disappointing for classification (tried applying concept on Sat. Log. Landsat(R, G, ir 1, ir 2, class). too few bands or classes? Still, I'm hoping for "Wow! Look at this!" when, e. g. , classes aren't known/clear and there are thousands of them and millions of bands. . . ) e. g. , 2 huge square-ish relationships to multi-hop. difficult (curse of dim = too many cols which are the relevant? ) rule mining comes into its own. One last thought: regarding " the curse of dimensionality = too many columns - which are the relevant ones? ", FAUST automatically filters irrelevant cols to find those that reveal [convex] classes (all good classes are convex in proper feature space. e. g. , Class=yellow_car may round-ish in Pix(Red. Wave. Len, Green. Wave. Len, Blue. Wave. Len, Other. Wave. Lens), once R, G, B are isolated as relevant ones. Class=pavement is fragmented in Pix(RWL, GWL, BWL, OWLs) but may be convex in WL(pix_x, pix_y) (because pavement is color consistent? ) Last point: We have to get you a FAUST implementation! It almost has to be orders of magnitude faster than pknn! The speedup should be very sublinear - almost constant (nearly independent of cardinality) - because it is a bulk classifier (one horizontal pass gains us a class_mask_p. Tree, distinguishing all points predicted to be in that class). So, not only is it model-based, but it is a batch classifier. Model-based classifiers that require scanning horizontal datasets cannot compete! Mark 3/2/12: Very close on faust. WP: it's important the classification step be done in bulk lest you lose the main huge benefit of FAUST. W hat happens at the end if you've peeled off all the classes and there are still some unclassified points left? have “mixed”/“default” (e. g. , Sat. Log class=6=“mixed”) potential interest from some folks who have close relationship with Arbitron. Seems like a netflix story to me. . .
User. Table(u. ID, m 1, . . . , m 17770) u. ID rating date u i 1 rmk, u dmk, u ui 2 . . . ui n k m. ID u. ID rating date m 1 u 1 rm, u dm, u m 1 u 2 . . . m 17770 u 480189 r 17770, 480189 d 17770, 480189 or U 2649429 MTbl(m. ID, u 1. . . u 480189) u 1 uk u 480189 m 1 rm rmhuk . 1/0 . 1 2 4 324513? 45 5 5 . u . 1 2 4 324513? 45 5 5 huk . m 17770 . 47 B u 480189 MPTree. Set 3*480189 bitslices wide u 0, 2 u 480189, 0 m 1 47 B u 480189 47 B (u, m) to be predicted, form um. Training. Tbl=Sub. UTbl(Support(m), Support(u), m) : m h : : uk u : m h : m 0, 2 . m 17769, 0 m u 1 : uk Main: (m, u, r, d) avg: 209 m/u ---- 100, 480, 507 ---- mk(u, r, d) avg: 5655 u/m UPTree. Set 3*17770 bitslices wide m 1 . . . mh . . . m 17770 m u 1 Netflix data {mk}k=1. . 17770 Lots of 0 s in vector sp, um. Traning. Tbl). Want the largest subtable without zeros. How? 0/1 m 17770 Sub. UTbl( n Sup(u) m. Sup(n), Sup(u), m)? 47 B Of course, the two supports won't be tight together like that but they are put that way for clarity. (u, m) to be predicted, from um. Training. Tbl = Sub. UTbl(Support(m), Support(u), m) Using Coordinate-wise FAUST (not Oblique), in each coordinate, n Sup(u), divide up all users v Sup(n) Sup(m) into their rating classes, rating(m, v). then: 1. calculate the class means and stds. Sort means. 2. calculate gaps 3. choose best gap and define cutpoint using stds. Coord FAUST, in each coord, v Sup(m), divide up all movies n Sup(v) Sup(u) to rating classes 1. calculate the class means and stds. Sort means. 2. calculate gaps 3. choose best gap and define cutpoint using stds. This of course may be slow. How can we speed it up? Gaps alone not best (especially since the sum of the gaps is no more than 4 and there are 4 gaps). Weighting (correlation(m, n)-based) useful (higher the correlation the more significant the gap? ? ) Ctpts constructed for just this one prediction, rating(u, m). Make sense to find all of them. Should just find, e, g, which n-class-mean(s) rating(u, n) is closest to and make those the votes?
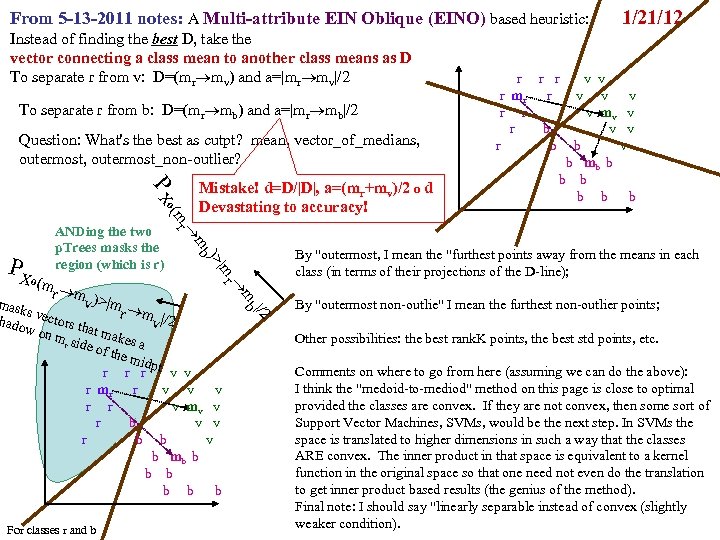From 5 -13 -2011 notes: A Multi-attribute EIN Oblique (EINO) based heuristic: 1/21/12 Instead of finding the best D, take the vector connecting a class mean to another class means as D To separate r from v: D=(mr mv) and a=|mr mv|/2 To separate r from b: D=(mr mb) and a=|mr mb|/2 Question: What's the best as cutpt? mean, vector_of_medians, outermost, outermost_non-outlier? mr o( PX |m r t mak es of th a e mid pt r r r v v r mr r v v v r r v mv v r b v v r b b v b mb b b b b b b on m r side For classes r and b |/2 mb (m r m )> v |m mask s vec r m |/2 tors t hado v ha w )> mb PXo ANDing the two p. Trees masks the region (which is r) Mistake! d=D/|D|, a=(mr+mv)/2 o d Devastating to accuracy! r r r v v r mr r v v v r r v mv v r b v v r b b v b mb b b b b b b By "outermost, I mean the "furthest points away from the means in each class (in terms of their projections of the D-line); By "outermost non-outlie" I mean the furthest non-outlier points; Other possibilities: the best rank. K points, the best std points, etc. Comments on where to go from here (assuming we can do the above): I think the "medoid-to-mediod" method on this page is close to optimal provided the classes are convex. If they are not convex, then some sort of Support Vector Machines, SVMs, would be the next step. In SVMs the space is translated to higher dimensions in such a way that the classes ARE convex. The inner product in that space is equivalent to a kernel function in the original space so that one need not even do the translation to get inner product based results (the genius of the method). Final note: I should say "linearly separable instead of convex (slightly weaker condition).
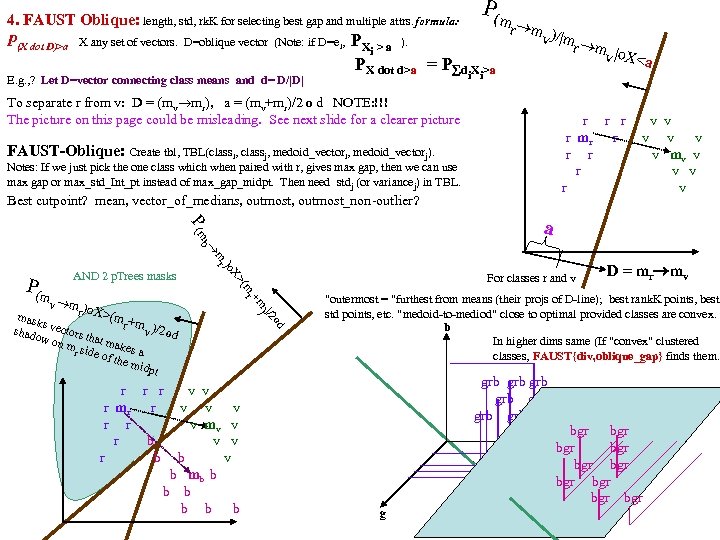4. FAUST Oblique: length, std, rk. K for selecting best gap and multiple attrs. formula: P(X dot D)>a X any set of vectors. D=oblique vector (Note: if D=ei, PX > a ). i E. g. , ? Let D=vector connecting class means and d= D/|D| P(m PX dot d>a = P d X >a i i To separate r from v: D = (mv mr), a = (mv+mr)/2 o d NOTE: !!! The picture on this page could be misleading. See next slide for a clearer picture FAUST-Oblique: Create tbl, TBL(classi, classj, medoid_vectori, medoid_vectorj). Notes: If we just pick the one class which when paired with r, gives max gap, then we can use max gap or max_std_Int_pt instead of max_gap_midpt. Then need stdj (or variancej) in TBL. Best cutpoint? mean, vector_of_medians, outmost_non-outlier? r m )/ v |m r m |o v X< a r r r v v r mr r v v v r r v mv v r v v r v P (m b a For classes r and v +m (m r X> od w on rs that m akes m si r de of th a e mid pt r r r v v r mr r v v v r r v mv v r b v v r b b v b mb b b b b b b od hado |/2 ) v m )o r X>(m mask s vec r +mv )/2 to s )o mr P(m AND 2 p. Trees masks D = mr mv "outermost = "furthest from means (their projs of D-line); best rank. K points, best std points, etc. "medoid-to-mediod" close to optimal provided classes are convex. b In higher dims same (If "convex" clustered classes, FAUST{div, oblique_gap} finds them. grb grb bgr D bgr grb bgr g r
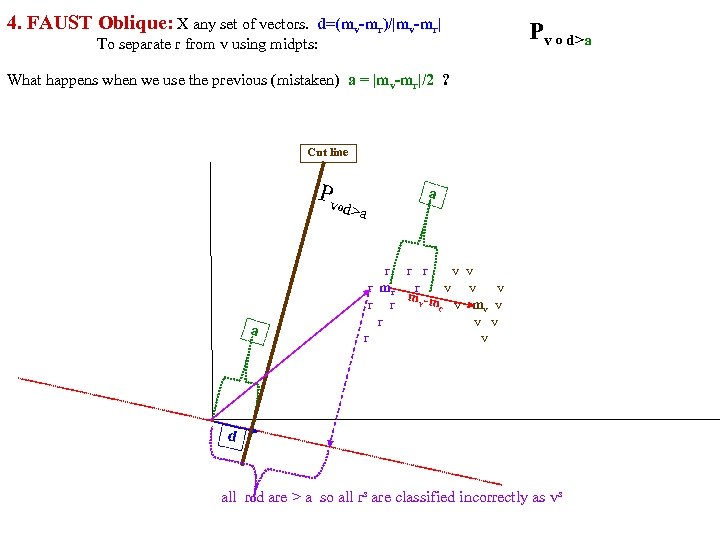4. FAUST Oblique: X any set of vectors. d=(mv-mr)/|mv-mr| To separate r from v using midpts: Pv o d>a What happens when we use the previous (mistaken) a = |mv-mr|/2 ? Cut line Pvo d>a a a r r r v v r mr r v v v mv -m r r v mv v r r v v r v d all rod are > a so all rs are classified incorrectly as vs = P di. Xi>a
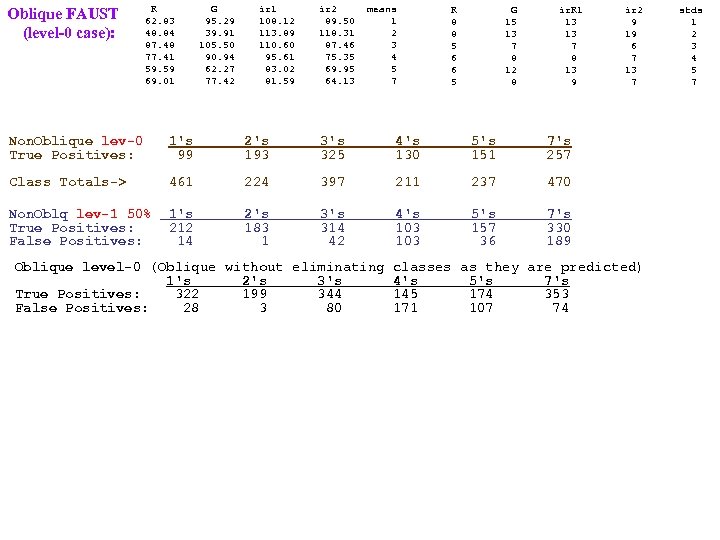Oblique FAUST (level-0 case): R G ir 1 ir 2 means 62. 83 95. 29 108. 12 89. 50 1 48. 84 39. 91 113. 89 118. 31 2 87. 48 105. 50 110. 60 87. 46 3 77. 41 90. 94 95. 61 75. 35 4 59. 59 62. 27 83. 02 69. 95 5 69. 01 77. 42 81. 59 64. 13 7 R G ir. R 1 ir 2 stds 8 15 13 9 1 8 13 19 2 5 7 6 3 6 8 7 4 6 12 13 5 5 8 9 7 Non. Oblique lev-0 1's 2's 3's 4's 5's 7's True Positives: 99 193 325 130 151 257 Class Totals-> 461 224 397 211 237 470 Non. Oblq lev-1 50% 1's 2's 3's 4's 5's 7's True Positives: 212 183 314 103 157 330 False Positives: 14 1 42 103 36 189 Oblique level-0 (Oblique without eliminating classes as they are predicted) 1's 2's 3's 4's 5's 7's True Positives: 322 199 344 145 174 353 False Positives: 28 3 80 171 107 74
Oblique FAUST (level-0 case): R G ir 1 ir 2 means 62. 83 95. 29 108. 12 89. 50 1 48. 84 39. 91 113. 89 118. 31 2 87. 48 105. 50 110. 60 87. 46 3 77. 41 90. 94 95. 61 75. 35 4 59. 59 62. 27 83. 02 69. 95 5 69. 01 77. 42 81. 59 64. 13 7 R G ir. R 1 ir 2 stds 8 15 13 9 1 8 13 19 2 5 7 6 3 6 8 7 4 6 12 13 5 5 8 9 7 Non. Oblique lev-0 1's 2's 3's 4's 5's 7's True Positives: 99 193 325 130 151 257 Class Totals-> 461 224 397 211 237 470 Non. Oblq lev-1 50% 1's 2's 3's 4's 5's 7's True Positives: 212 183 314 103 157 330 False Positives: 14 1 42 103 36 189 Midpt Oblique level-0 (Oblique without eliminating classes as they are predicted) 1's 2's 3's 4's 5's 7's True Positives: 322 199 344 145 174 353 False Positives: 28 3 80 171 107 74 Coordinatewise STDs Oblique level-0 (w/o class elimination) 1's 2's 3's 4's 5's 7's True Positives: 239 194 351 145 170 0<-probably False Positives: 24 0 148 182 91 0<-mistakes) projected STDs Oblique level-0 (w/o class elimination) 1's 2's 3's 4's 5's 7's True Positives: 359 205 332 144 175 324 False Positives: 29 18 47 156 131 58 projected STDs Oblique level-0 (with class elimination in 2, 3, 4, 5, 6, 7, 1 order) 1's 2's 3's 4's 5's 7's True Positives: 359 205 332 144 175 324 False Positives: 29 18 47 156 131 58
MYRRH A hop is relationship, R ( hops from one entity, E, to another, F). 1/7/12 Strong Rule Mining (SRM) finds all frequent and confident rules, A C (Non-transitive if A, C E (the ARM case). Transitive if A E, C F) Frequency can lower bound the antecedent, consequent or both (ARM = both: ct(&e A CRe) mnsp) 2 4 3 2 1 E 3 4 5 0 0 1 0 0 0 F 0 1 0 R(E, F) Its justification is the elimination of insignificant cases. Its purpose is the tractability of SRM. Confidence lower bds the frequency of both over the frequency of the antecedent, ct(&e ARe&e CRe)/ct(&e ARe) mncf The crux of SRM is frequency counts. To compare these counts meaningfully they must be on the same entity (focus entity). SRMs are categorized by the number of hops, k, whether transitive or non-transitive and by the focus entity. ARM is 1 -hop, E-non-transitive (A, C E) and F-focused SRM (1 n. F) (How does one define non-transitive in for multi-hop SRM? ) 1 -hop, transitive (A E, C F), F-focused SRM (1 t. F) APRIORI: ct(&e ARe) mnsp ct(&e ARe &PC) / ct(&e ARe) mncf 1. (antecedent downward closure) If A is frequent, all of its subsets are frequent. Or, if A is infrequent, then so are all of its supersets. Since frequency involves only A, we can mine for all qualifying antecedents efficiently using downward closure. 2. (consequent upward closure) If A C is non-confident, then so is A D for all subsets, D, of C. So frequent antecedent, A, use upward closure to mine for all of its' confident consequents. The theorem we demonstrate throughout this section is: For transitive (a+c)-hop Apriori strong rule mining with a focus entity which is a hops from the antecedent and c hops from the consequent, if a/c is odd/even then one can use downward/upward closure on that step in the mining of strong (frequent and confident) rules. In this case A is 1 -hop from F (odd, use downward closure). C is 0 -hops from F (even, use upward closure). We will be checking more examples to see if the Odd downward Even upward theorem seems to hold. 1 -hop, transitive, E-focused rule, A C SRM (1 t. E) |A|=ct(PA) mnsp ct(PA&f CRf) / ct(PA) mncf 1. (antecedent upward closure) If A is infrequent, then so are all of its subsets. 2. (consequent downward closure) If A C is non-confident, then so is A D for all supersets, D, of C. In this case A is 0 -hops from E (even, use upward closure). C is 1 -hop from E (odd, use downward closure).
2 -hop transitive F-focused (focus on middle entity, F) 2 t. F ct(&e ARe) mnsp 1 1 0 1 1. (antecedent downward closure) If A is infrequent, then so are all of its supersets. 2. (consequent downward closure) If A C is non-confident, so is A D for all supersets, D. A E 4 3 2 1 1 0 0 0 1 1 2 ct(&e ARe &g CSg) / ct(&e ARe) mncf 3. Apriori for 2 -hops: Find all freq antecedents, A, using downward closure. For each: find C 1 G, the set of g's s. t. A {g} is confident. Find C 2 G, the set of C 1 G pairs that are confident consequents for antecedent, A. Find C 3 G, the set of triples (from C 2 G) s. t. all subpairs are in C 2 G (ala Apriori), etc. C G S(F, G) A C strong if: 3 4 5 0 0 0 0 1 4 3 2 1 F R(E, F) The number of hops from the focus are 1 and 1, both odd so both have downward closure. Standard ARM can be viewed as 2 t. F where E=G, A C empty and S=Rtr. Thus, we have no non-transitive situation anymore, so we can drop the t verses n and call this 2 F 2 G ct(&f &e ARe. Sf) mnsp ct(&f &e ARe. Sf & PC) / &f & S e ARe f 1. (antecedent upward closure) If A is infrequent, then so for are all subsets. 2. (consequent upward closure) If A C is non-confident, so is A D for all subsets, D. 2 E ct(PA) mnsp ct(PA&f &g CSg. Rf ) / ct(PA) mncf 1. (antecedent upward closure) If A is infrequent, then so for are all subsets. 2. (consequent upward closure) If A C is non-confident, so is A D for all subsets, D. mncf The number of hops from the focus are 2 and 0, both even so both have upward closure. The number of hops from the focus are 0 and 2, both even so both have upward closure.
3 -hop Collapse T: TC≡ {g G|T(g, h) h C} That's just 2 -hop case w TC G replacing C. ( can be replaced by or any other quantifier. The choice of quantifier should match that intended for C. ). Collapse T and S: STC≡{f F |S(f, g) g TC} Then it's 1 -hop w STC replacing C. 2 S(F, G) 3 4 5 0 0 1 0 0 0 1 1 0 1 G 1 1 0 1 0 0 0 1 1 2 3 4 4 3 2 1 0 0 0 0 1 0 1 A E 3 F ct(&e ARe mnsp ct(&e ARe g & & S) h CTh g /ct(&e ARe mncf 5 4 3 2 1 0 0 1 0 T(G, H) F H C 0 0 1 0 antecedent downward closure: A infreq. implies supersets infreq. A 1 -hop from F (down consequent upward closure: A C noncnf implies A D noncnf. D C. C 2 -hops (up 3 G ct(&f &e ARe. Sf) mnsp ct(&f & S e ARe f &h CTh) /ct(&f & S) e ARe f mncf antecedent upward closure: A infreq. implies all subsets infreq. A 2 -hop from G (up) consequent downward closure: A C noncnf impl A D noncnf. D C. C 1 -hops (down) R(E, F) Focus on F Are they different? Yes, because the confidences can be different numbers. Focus on G. ct(&e ARe &g list&h CTh. Sg ) /ct(&e ARe ct( 1001 &g=1, 3, 4 Sg ) /ct(1001) ct( 1001 &1001&1000&1100) / 2 ct( 1000 ) / 2 = 1/2 3 E ct(PA) mnsup ct(&f list&e ARe. Sf &h CTh) ct(&f=2, 5 Sf &1101 ) & ct(1101 & 0011 &1101 ) ) ct(0001 / ct(&f list&e ARe. Sf) / ct(&f=2, 5 Sf / ct(1101 & 0011 ) / ct(0001) = 1/1 =1 ct(PA & Rf) / ct(PA) mncnf f & S g &h CTh g antecedent upward closure: A infreq. implies subsets infreq. A 0 -hops from E (up) consequent downward closure: A C noncnf implies A D noncnf. D C. C 3 -hops (down) 3 H /ct(& Tg) mncnf ct(& Tg) mnsp ct(& Tg & PC) g & S S g & S f &e ARe f antecedent downward closure: A infreq. implies all subsets infreq. A 3 -hops from G (down) consequent upward closure: A C noncnf impl A D noncnf. D C. C 0 -hops (up) f &e ARe f
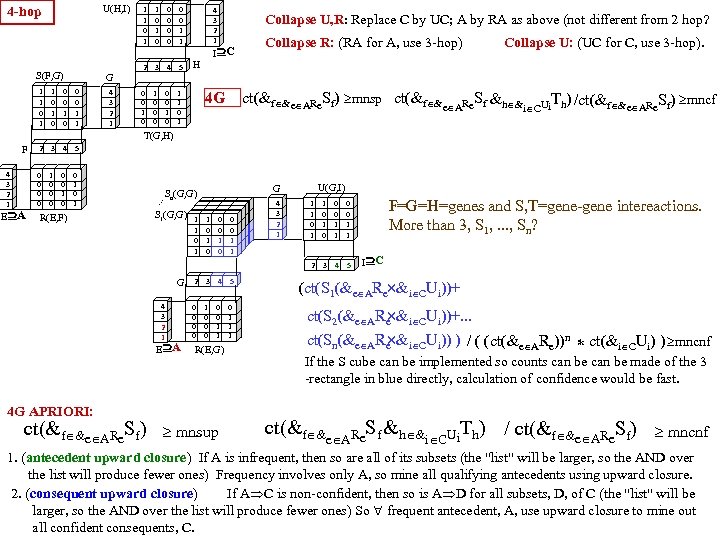4 -hop U(H, I) 1 0 0 0 0 1 1 2 S(F, G) 1 1 0 1 3 4 5 0 0 1 0 0 0 1 1 0 1 4 3 2 1 Collapse U, R: Replace C by UC; A by RA as above (not different from 2 hop? Collapse R: (RA for A, use 3 -hop) Collapse U: (UC for C, use 3 -hop). I C H G 1 1 0 1 0 0 0 1 1 2 3 4 5 0 0 0 0 1 0 1 4 3 2 1 0 0 1 0 ct(&f &e ARe. Sf) mnsp ct(&f &e ARe. Sf &h & 4 G T ) /ct(&f &e ARe. Sf) i CUi h mncf T(G, H) F 4 3 2 1 0 0 1 0 U(G, I) G Sn(G, G) R(E, F) . . . S 1(G, G) G 4 3 2 1 E A 1 1 0 0 1 11 00 00 00 1 0 0 0 1 00 11 11 11 0 0 1 1 1 0 11 00 00 11 1 1 0 0 0 1 1 3 4 5 F=G=H=genes and S, T=gene-gene intereactions. More than 3, S 1, . . . , Sn? 0 0 1 1 I C 2 3 4 5 (ct(S 1(&e ARe &i CUi))+ 0 0 0 0 1 1 1 ct(S 2(&e ARe &i CUi))+. . . ct(Sn(&e ARe &i CUi)) ) / ( (ct(&e ARe))n * ct(&i CUi) ) mncnf 0 0 1 1 R(E, G) 4 G APRIORI: ct(&f &e ARe. Sf) 4 3 2 1 1 1 0 1 2 E A mnsup If the S cube can be implemented so counts can be made of the 3 -rectangle in blue directly, calculation of confidence would be fast. ct(&f &e ARe. Sf &h & T) i CUi h / ct(&f &e ARe. Sf) mncnf 1. (antecedent upward closure) If A is infrequent, then so are all of its subsets (the "list" will be larger, so the AND over the list will produce fewer ones) Frequency involves only A, so mine all qualifying antecedents using upward closure. 2. (consequent upward closure) If A C is non-confident, then so is A D for all subsets, D, of C (the "list" will be larger, so the AND over the list will produce fewer ones) So frequent antecedent, A, use upward closure to mine out all confident consequents, C.
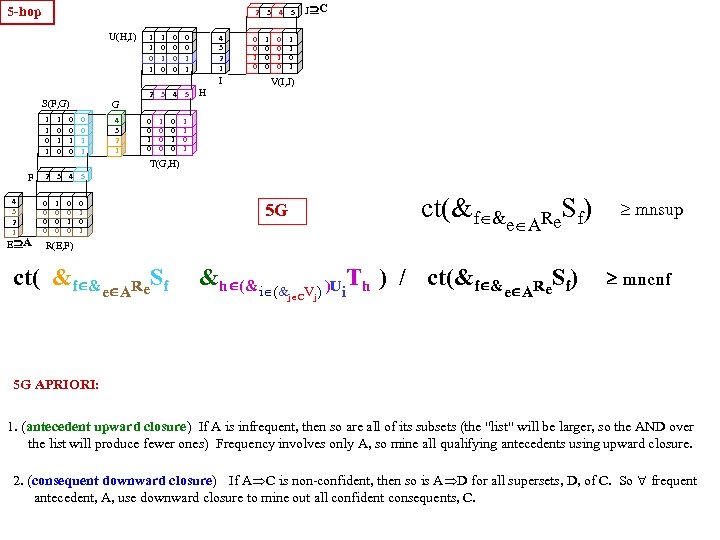5 -hop 2 U(H, I) 1 1 0 1 0 0 0 0 1 1 2 3 4 5 0 0 1 0 1 0 0 0 J C 1 1 0 1 4 3 2 1 I S(F, G) 3 4 H 0 0 1 0 V(I, J) G 1 1 0 1 0 0 0 1 1 2 3 4 5 0 0 0 0 1 0 1 4 3 2 1 0 0 1 0 T(G, H) F 4 3 2 1 E A 0 0 1 0 ct(&f & 5 G S) e ARe f mnsup R(E, F) ct( &f & S e ARe f &h (& )U Th ) / ct(&f & i (& V ) j C j i S) e ARe f mncnf 5 G APRIORI: 1. (antecedent upward closure) If A is infrequent, then so are all of its subsets (the "list" will be larger, so the AND over the list will produce fewer ones) Frequency involves only A, so mine all qualifying antecedents using upward closure. 2. (consequent downward closure) If A C is non-confident, then so is A D for all supersets, D, of C. So frequent antecedent, A, use downward closure to mine out all confident consequents, C.
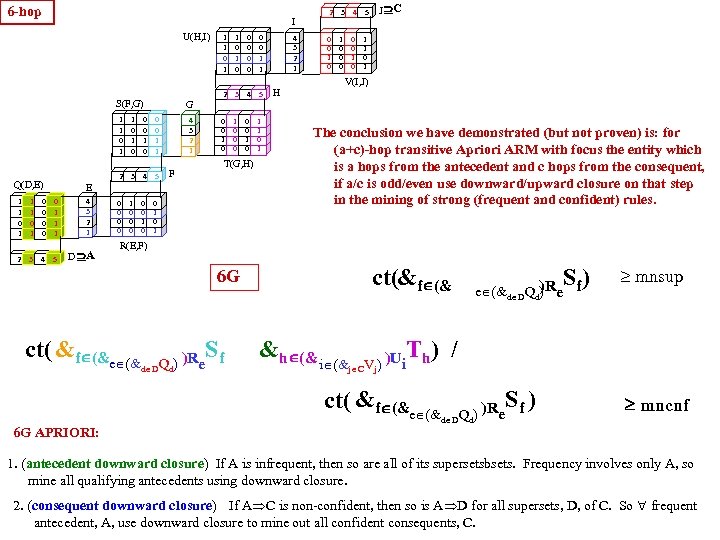6 -hop I U(H, I) 0 0 0 1 1 3 4 5 0 0 1 0 0 0 1 1 2 3 4 5 0 0 0 0 1 0 1 4 3 2 1 F 1 1 0 0 0 1 1 1 2 3 4 5 4 3 2 1 D A 0 0 1 0 T(G, H) E 1 1 0 1 4 3 2 1 H 3 4 0 0 1 0 0 0 J C 5 1 1 0 0 1 0 V(I, J) G 1 1 0 1 Q(D, E) 1 0 2 S(F, G) 1 1 0 1 2 The conclusion we have demonstrated (but not proven) is: for (a+c)-hop transitive Apriori ARM with focus the entity which is a hops from the antecedent and c hops from the consequent, if a/c is odd/even use downward/upward closure on that step in the mining of strong (frequent and confident) rules. R(E, F) ct(&f (& )R Sf) e (& Q ) 6 G d D d e mnsup & e (& Q ) ct( f (& )Re. Sf &h (& )U Th) / i (& V ) d D d j C j i & e (& Q ) ct( f (& )Re. Sf ) d D d mncnf 6 G APRIORI: 1. (antecedent downward closure) If A is infrequent, then so are all of its supersetsbsets. Frequency involves only A, so mine all qualifying antecedents using downward closure. 2. (consequent downward closure) If A C is non-confident, then so is A D for all supersets, D, of C. So frequent antecedent, A, use downward closure to mine out all confident consequents, C.
Given any 1 -hop labeled relationship (e. g. , cells have values from {1, 2, …, n} then there is: R 5(C, M) 1. a natural n-hop transitive relationship, A D, by alternating entities for each individual label value bitmap relationships. 2. cards for each entity consisting of the bitslices of cell values. E. g. , netflix, Rating(Customer, Movie) has label set {0, 1, 2, 3, 4, 5}, so in 1. it generates a bonafide 6 -hop transitive relationship. R 3(C, M) D F A E 4 3 2 1 0 0 2 3 4 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 1 0 0 1 R 0(E, F) Rn-2(E, F) Rn-1(E, F) R 1(C, M) 1 1 0 1 0 0 0 1 1 3 4 5 0 0 0 0 1 0 1 M 0 1 1 1 4 3 2 1 C A 0 0 1 0 1 0 0 0 0 1 1 3 4 5 0 0 1 0 0 0 2 3 4 5 0 0 1 0 C D 1 1 0 1 4 3 2 1 C R 0(M, C) M 1 0 2 5 1 1 0 1 2 1 1 0 1 . . . Below, as in 2. , Rn-i can be bitslices M R 2(M, C) 4 3 2 1 C 0 0 1 0 R 4(M, C) R 1(A)= "Movies rated 1 by all customers in A. R 2(R 1(A))= "Cust who rate as 2, all R 1(A) movies" = "Cust who rate as 2, all movies rated as 1 by all A-cust". R 3(R 2(R 1(A)))= "Movies rated as 3 by all R 2(R 1(A)) customers" = "Movies rated as 3 by all customers who rate as 2 all movies rated as 1 by all A-customers". R 4(R 3(R 2(R 1(A))))= "Customers who rate as 4 all R 3(R 2(R 1(A))) movies" = "Customers who rate as 4 movies rated as 3 by all customers who rate as 2 all movies rated as 1 by all A-customers". 2 3 4 5 R 5(R 4(R 3(R 2(R 1(A)))))= "Movies rated as 5 by all R 4(R 3(R 2(R 1(A)))) customers" = "Movies rated 5 by all customers who rate as 4 movies rated as 3 by all customers who rate as 2 all movies rated as 1 by all A-customers". R 0(R 5(R 4(R 3(R 2(R 1(A))))))= R 0(R 5(R 4(R 3(R 2(R 1(A)))))) D "Customers who rate as 0 all R 5(R 4(R 3(R 2(R 1(A))))) movies" = "Cust who rate as 0 all movies rated 5 by all cust who rate as 4 movies rated as 3 by all cust who rate as 2 all movies rated as 1 by all A-cust". E. g. , equity trading on a given day, Quantity. Bought(Cust, Stock) w labels {0, 1, 2, 3, 4, 5} (where n means n thousand shares) so that generates a bonafide 6 -hop transitive relationship: E. g. , equity trading - moved similarly, (define moved similarly on a day --> Stock(#Days. Moved. Similarly. Of. Last 10) E. g. , equity trading - moved similarly 2, (define moved similarly to mean that stock 2 moved similarly to what stock 1 did the previous day. Define relationship Stock(#Days. Moved. Similarly. Of. Last 10) E. g. , Gene-Experiment, Label values could be "expression level". Intervalize and go! Has Strong Transitive Rule Mining (STRM) been done? Are their downward and upward closure theorems already for it? Is it useful? That is, are there good examples of use: stocks, gene-experiment, MBR, Netflix predictor, . . .
Buys(C, T) =1 iff t D s. t. B(c, t)=1, B(c, t)=1 E. g. , in a store, Types might include; dairy, hardware, household, canned, snacks, means i t s. t. BB(I, c)=1 Let Types be an entity which clusters Items (moves Items up the semantic hierarchy), baking, meats, produce, bakery, automotive, electronics, toddler, boys, girls, women, pharmacy, garden, toys, farm). Let A be an Item. Set wholly of one Type, TA, and l et D by a Types. Set which does not include TA. Then: A D might mean If i A s. t. BB(i, c) then t D, B(c, t) A D confident might mean ct(&i ABBi &t DBt) / ct(&i ABBi) mncf ct(&i ABBi | t DBt) / ct(&i ABBi) mncf ct( | i ABBi | t DBt) / ct( | i ABBi) mncf ct( | i ABBi &t DBt) / ct( | i ABBi) mncf D Types (of Items) 1 1 0 1 0 0 0 1 1 4 3 2 1 2 3 4 5 Customers 20 19 18 17 16 15 0 0 0 1 0 0 0 0 1 1 1 14 13 0 0 0 1 1 A Items 12 11 8 7 0 0 0 1 6 5 0 0 0 1 1 4 3 0 0 0 1 1 2 1 0 0 0 1 1 10 9 Bought. By(I, C, ) A D frequent might mean ct(&i ABBi) mnsp ct( | i ABBi) mnsp ct(&t DBt) mnsp ct( | t DBt) mnsp ct(&i ABBi &t DBt) mnsp, etc.
A thought on impure p. Trees (i. e. , with predicate, 50%ones). The training set was ordered by class (all setosa's came first, then all versicolor then all virginica) so that level_1 p. Trees could be chosen not to span classes much. Take an images as another example. If the classes are Red. Cars, Green. Cars, Blue. Cars, Parking. Lot, Grass, Trees, etc. , and if Peano ordering is used, what if a class spans Peano squares completely? We now create p. Trees from many different predicates. Should we created p. Tree. Sets for many different orderings as well? This would be a one time expense. It would consume much more space, but space is not an issue. With more p. Trees, our PGP-D protection scheme would automatically be more secure. So move the first column values to the far right for the 1 st additional Peano p. Tree. Set: Move the 1 st 2 columns to the right for 2 nd Peano p. Tree. Set, 1 st 3 for 3 rd Peano p. Tree. Set. .
Move the last column to the left for the 4 th, the last 2 left for the 5 th, the last 3 left for the 6 th additional Peano p. Tree. Set. For each of these 6 additional Peano p. Tree. Sets, make the same moves vertically (64 Peano p. Tree. Sets in all), e. g. , the 25 th would be (starting with the 4 th horizontal, directly above). For each of these 6
What about this? Looking at the vertical expansions of the 2 nd additional p. Tree. Set (the 13 th and 14 th additional p. Tree. Sets, respectively? ) Question: How are the training set classes given to us in Aurora, etc. ? My question is, are we just given a set of pixels that we're told are Green. Car pixels? Or are we given anything that would allow us to use shapes of Green. Cars to identify em? That is, are we given a traning set of Green. Car pixels together with their relative positions to one another - or anything like that? If we're given only pixel reflectance values for Green. Car, then we have to rely on individual pixel reflectances, right? In that case, we might as well just analyze each pixel for Green. Car characteristics. And then we would not benefit from this idea except that we might be able to data mine Green. Cars using level_2 only? ? The green car is now centered in a level_2 pixel, assuming the level_2 stride is 16 (and the level_1 stride is 4).
Notice that the left move 3 is the same as right move 1 (and left 2 is the same as right 2; left 1 is the same as right 3. ) Thus, we have only 42 = 16 orderings (not 64) at level-2; 41 = 4 at level-1; 4 n at level-n. Essentially the upper right corner can be in any one of the cells in a level-n pixel and there are 4 n such cells. If we always create pure 1, pure 0 (for complements of pure 1) and GTE 50% predicate trees, there would be 3*4 n separate PTree. Sets. Then the question is how to order pixels in a left (or up) shift? We could actually shift and then use the usual Peano? Or we could keep each cell ordering as much the same as possible (see below). One thought is to do the shifting at level-0, and percolate it upward. But we have to understand what that means. We certainly wouldn't store shifted level-0 PTree. Sets since they are the same pixelization. So: construct shifted level-n pixelizations (n>0) concurrently by considering, one at a time, all level-0 pixel shifts (creating an additional PTree. Set only when it is a new pixelization (e. g. , only the first level-0 pixel shift produces a new pixelization at level-1; only the first 3 at level-2, only the first 7 at level-3, etc. Throw away the bogus level-n pixels (e. g. , at right throw away right column of level-2 pixels since it isn't bonefide image). Start with a fresh Z-ordering (2 nd option).
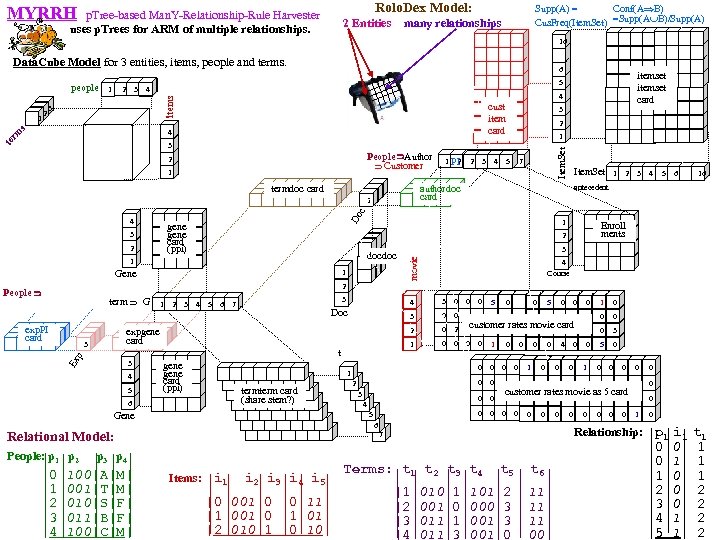Rolo. Dex Model: MYRRH p. Tree-based Man. Y-Relationship-Rule Harvester Conf(A B) Supp(A) = Cus. Freq(Item. Set) =Supp(A B)/Supp(A) 2 Entities many relationships uses p. Trees for ARM of multiple relationships. 16 2 1 3 6 itemset card 5 4 items people Item Data. Cube Model for 3 entities, items, people and terms. 3 2 1 cust item card te rm s 4 3 2 1 People Author Customer 2 1 termdoc card gene card (ppi) 3 2 1 1 authordoc 1 1 card 1 1 1 1 Gene 1 1 2 3 4 0 5 6 16 0 Enroll ments 2 1 1 docdoc 1 1 Item. Set antecedent 3 movie 4 1 1 PI 3 4 4 5 7 2 2 3 5 6 Do c 1 Item. Set 3 4 Course 2 People term G exp. PI card 1 3 4 5 6 3 7 4 3 0 0 Doc 3 0 0 2 2 0 2 1 0 0 0 expgene card 1 Ex 3 4 5 gene card (ppi) 6 4 5 0 1 0 0 0 0 0 1 0 0 Items: i 1 i 2 i 3 i 4 i 5 0 0 Terms: t 1 t 2 t 3 t 4 4 0 0 0 1 3 5 0 0 0 customer rates movie as 5 card 0 0 0 1 0 Relationship: p 1 i 1 t 1 7 People: p 1 p 2 p 3 p 4 0 customer rates movie card 0 3 0 6 Relational Model: |0 100|A|M| |1 001|T|M| |2 010|S|F| |3 011|B|F| |4 100|C|M| 0 0 2 5 Gene 5 0 1 term card (share stem? ) 0 0 t p 3 1 t 5 t 6 |1 010|1 101|2 11| |0 001|0 |0 11| |2 001|0 000|3 11| |1 001|0 |1 01| |3 011|1 001|3 11| |2 010|1 |0 10| |4 011|3 001|0 00| |0 0| 1 |0 1| 1 |1 0| 1 |2 0| 2 |3 0| 2 |4 1| 2 |5 1|_2
APPENDIX: MYRRH_2 e_2 r (standard p. ARM is MYRRH_2 e_1 r ) pre-computed Bp. Ttreec 1 -counts 3 e. g. , Rate 5(Cust, Book) or R 5(C, B), Purchase(Book, Cust) or P(B, C) Bp. Ttreeb 1 -cts 2 1 1 0 0 Given e E, If R(e, f), then S(e, f) ct(Re & Se)/ct(Re) mncnf, ct(Re)/sz(Re) mnsp If e A R(e, f), then e B S(e, f) ct( &e ARe &e BSe) / ct(&e ARe) mncnf. . If e A R(e, f), then e B S(e, f) ct( &e ARe ORe BSe) / ct(&e ARe) mncnf. . If e A R(e, f), then e B S(e, f) pre-com. R 5 p. Ttreeb 1 -cts 1 1 3 4 5 0 0 0 0 1 0 ct( ORe ARe ORe BSe) / ct(ORe ARe) mncnf. . 1 1 B=2 B=3 B=4 0 1 1 2 P 1={B=1|2} P 2={B=3|4} C 1 0 1 C 2 1 0 0 1 1 0 0 1 4 3 C (E) 2 1 B R 5(C, B) (F) (R(E, F)) 2 1 0 R 5(C, B) R 5 p. Ttreeb&Pp. Treeb 1 1 -counts 1 Consder 2 Customer classes, Class 1={C=2|3} and Class 2={C=4|5}. Then P(B, C) is Training. Set: Then the Diff. Sup table is: (S(E, F)) R 5 p. Ttreec 1 -cts Schema: size(C)=size(R 5 p. Treeb)=size(Bp. Treeb)=4 size(B)= size(R 5 p. Treec)=size(Bp. Treec)=4 ct( ORe ARe &e BSe) / ct(ORe ARe) mncnf. . If e A R(e, f), then e B S(e, f) P(B, C) 1 0 0 0 3 2 2 1 1 2 1 If cust, c, rates book, b as 5, then c purchase b. For b B, {c| rate 5(b, c)=y} {c| purchase(c, b)=y} ct(R 5 p. Treei & Pp. Treei) / ct(R 5 p. Treei) mncnf ct(R 5 p. Treei) / sz(R 5 p. Treei) mnsp Speed of AND: R 5 p. Tree. Set & Pp. Tree. Set? (Compute each ct(R 5 p. Treeb&Pp. Treeb). ) Slice counts, b B, ct(R 5 p. Treeb & Pp. Treeb) w AND? 2 1 Book=4 is very discriminative of Class 1 and Class 2, e. g. , Class 1=salary>$100 K P(B, C) 1 1 0 0 0 0 1 1 1 0 0 0 1 CB 1 2 3 4 2 1 0 1 1 3 0 1 4 0 1 0 0 5 1 1 0 0 P 1 [and P 2, B=2 and B=3] is somewhat discriminative of the classes, whereas B=1 is not. . DS 1 1 Are "Discriminative Patterns" covered by ARM? E. g. , does the same information come out of strong rule mining? Does "DP" yield information across multiple relationships? E. g. , determining the classes via the other relationship?
Making 3 -hops: Use 4 feature attributes of an entity. For IRIS(SL, SW, PL, PW). L(SL, PL), P(PL, PW), W(PW, SW) Let A SL be {6, 7} and C PW be {1, 2} SW=0 1 2 3 4 5 6 7 PW S 0 0 0 0 0 0 1 1 0 0 0 P 0 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 2 0 0 0 1 1 0 0 0 0 0 3 0 0 0 0 0 1 0 0 0 4 0 0 0 0 5 0 0 0 0 6 0 0 0 0 7 0 0 0 0 PL=0 1 2 3 4 5 6 7 PL=0 0 0 0 1 0 0 L 1 0 0 0 0 2 0 0 0 0 3 0 0 0 0 4 0 1 0 0 0 5 0 0 1 0 0 6 0 0 0 1 1 1 0 0 7 0 0 0 1 1 0 SL stride=10 level-1 val SL SW PL PW setosa 38 38 14 2 setosa 50 38 15 2 setosa 50 34 16 2 setosa 48 42 15 2 setosa 50 34 12 2 versicolor 1 24 45 15 versicolor 56 30 45 14 versicolor 57 28 32 14 versicolor 54 26 45 13 versicolor 57 30 42 12 virginica 73 29 58 17 virginica 64 26 51 22 virginica 72 28 49 16 virginica 74 30 48 22 virginica 67 26 50 19 SL SW PL rnd(PW/10) 4 4 1 0 5 4 2 0 5 3 2 0 5 4 2 0 5 3 1 0 0 2 5 2 6 3 5 1 6 3 3 1 5 3 5 1 6 3 4 1 7 3 6 2 6 3 5 2 7 3 5 1 7 3 5 2
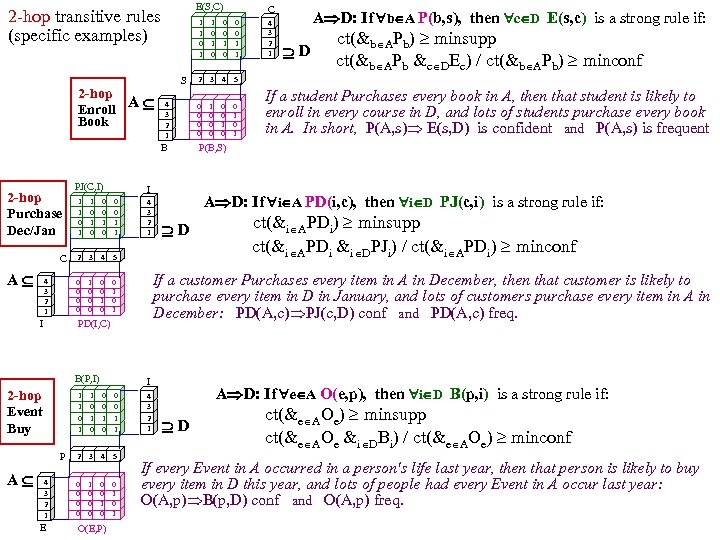E(S, C) 2 -hop transitive rules (specific examples) 2 -hop Enroll A Book S 4 3 2 1 B 2 -hop Purchase Dec/Jan I 4 3 2 1 I 1 1 0 1 0 0 0 1 1 2 3 4 1 0 0 1 0 2 -hop Event Buy P 4 3 2 1 E 1 0 0 0 1 1 2 3 4 5 0 0 0 0 1 0 1 0 O(E, P) D I 1 1 0 0 0 1 1 2 3 4 0 0 0 0 1 0 1 A D: If b A P(b, s), then c D E(s, c) is a strong rule if: 5 0 0 1 0 4 3 2 1 D ct(&b APb) minsupp ct(&b APb &c DEc) / ct(&b APb) minconf If a student Purchases every book in A, then that student is likely to enroll in every course in D, and lots of students purchase every book in A. In short, P(A, s) E(s, D) is confident and P(A, s) is frequent P(B, S) ct(&i APDi) minsupp ct(&i APDi &i DPJi) / ct(&i APDi) minconf If a customer Purchases every item in A in December, then that customer is likely to purchase every item in D in January, and lots of customers purchase every item in A in December: PD(A, c) PJ(c, D) conf and PD(A, c) freq. PD(I, C) B(P, I) A 4 3 2 1 1 0 A D: If i A PD(i, c), then i D PJ(c, i) is a strong rule if: 5 0 0 C A PJ(C, I) C 1 1 0 1 4 3 2 1 A D: If e A O(e, p), then i D B(p, i) is a strong rule if: D ct(&e AOe) minsupp ct(&e AOe &i DBi) / ct(&e AOe) minconf If every Event in A occurred in a person's life last year, then that person is likely to buy every item in D this year, and lots of people had every Event in A occur last year: O(A, p) B(p, D) conf and O(A, p) freq.
T(S, M) 2 -hop stock trading A 4 3 2 1 E 1 0 0 0 1 1 2 3 4 5 0 0 S 1 0 0 1 0 O(E, S) T(C, M) 2 -hop commodity trading A E 1 0 0 0 1 1 2 3 4 5 0 0 4 3 2 1 1 0 0 1 0 A D ct(&e AOe) minsupp ct(&e AOe &m DTm) / ct(&e AOe) minconf If every Event in A occurs for a company in time period 1, then the price of that stock experienced every move in D time period 2, and lots of companies had every Event in A occur in period 1: O(A, s) T(s, D) conf and O(A, s) freq. (T=True; e. g. , m=1 down a lot, m=2 down a little, m=3 up a little, m=4 up a lot. ) 4 3 2 1 A D: If e A O(e, c), then m D T(c, m) is a strong rule if: D ct(&e AOe) minsupp ct(&e AOe &m DTm) / ct(&e AOe) minconf If every Event in A occurs for a commodity in time period 1, then the price of that commodity experienced every move in D time period 2, and lots of commodities had every Event in A occur in period 1: O(A, c) T(c, D) conf and O(A, c) freq. O(E, C) B(P, I) 2 -hop facebook friends buying 4 3 2 1 M 1 1 0 1 C A D: If e A O(e, s), then m D T(s, m) is a strong rule if: M 1 1 0 1 A D: If p A P(p, q), then i D B(p, i) is a strong rule if: I 1 1 0 1 P 4 3 2 1 P 1 0 0 0 1 1 2 3 4 5 F(p, q)=1 iff q is a facebook friend of p. B(p, i)=1 iff p buys item i. 0 0 0 0 1 0 1 People befriended by everyone in A (= &p AFp denoted FA for short ) likely buy everything in D. And FA is large. 0 0 1 0 F(P, P) 4 3 2 1 D ct(&p AFp) minsupp ct(&p AFp &i DBi) / ct(&p AFp) minconf So every time a new person appears in FA that person is sent ads for items in D.
How do we construct interesting 2 -hop examples? Method-1: Use a feature attribute of a 1 -hop entity. Start with a 1 -hop, e. g. , customers buy items, stocks have prices or people befriend people then focus on one feature attribute of one of the entities. The relationship is the projection of that entity table onto the feature attribute and the entity id attribute (key) e. g. Age, Gender, Income Level, Ethnicity, Weight, Height. . . of people or customer entity These are not bonafide 2 -hop transitive relationships since they are many-to-one relationships, not a many-to-many (because the original entity is the primary key of its feature table). Thus, we don't get a fully transitive relationship since collapsing the original entity leaves nearly the same information as the transitive situation was intended to add. Here is an example. If, from the new transitive relationship, Age Is. Age. Of Customer Purchased Item, Customer is collapsed we have Age Purchase Item and the Customer-to-Age info is still available to us in the Cust table. The relationship between Customers and Items is lost, but presumably, the reason for mining, Age Is. Age. Of Customer Purchase Item is to find Age Purchase Item rules independent of the Customers involved. Then when a high confidence Age implies Item rule is found, the Customers who are of that age can be looked up from the Customer feature table and sent a flyer for that item. Also, in Customer Purchase Item, the antecedent, A, could have been chosen to be an age-group. So most Age Purchase Item info would come out of Customer Purchase Item directly. Given a 1 -hop relationship, R(E, F) and a feature attribute, A of E, if there is a pertinent way to raise E up the semantic hierarchy (cluster it) producing E', then the relationship between A and E ' is many-to-many, e. g. , cluster Customers by Income Level, IL. Then Age Is. Age. Of IL is a many-to-many relationship. Note, what we're really doing here is using the many-to-many relationship between two feature attributes in one of the entity tables and then replacing the entity by the second feature. E. g. , if B(C, I) is a relationship, and IL is a feature attribute in the entity table C(A, G, IL, E, W, H), then clustering (Classifying) C by IL produces a relationship, B'(IL, I), given by B'(il, i)=1 iff B(c, i)=1 for 50% of c il, which is many-to-many provided IL is not a candidate key. So from the 1 -hop relationship, C B(C, I) I, we get a bonafide 2 hop relationship, A AO(A, IL) IL B'(IL, I) I. B(C, I) 1 1 0 1 C A IL 1 0 0 0 1 0 B'(IL, I) I 0 0 1 1 0 1 4 3 2 1 IL 2 3 4 5 5 1 2 3 2 1 0 1 1 0 0 1 2 3 5 4 Bil=1 = Bc=2 Bil=3 = Bc=4 1 1 1 0 I A ct(&a AAOe) mnsp 4 C ct( AOa=4) mnsp 3 2 ct( 010) mnsp 1 1 mnsp Bil=2 = Bc=3 OR Bc=5 I AO(A, IL) So these are different rules. ct(&c C(A)Bc) mnsp ct( Bc=3 ) mnsp ct( 0101 ) mnsp 2 mnsp ct(&a AAOa&g CB'g)/ct(&a AAOa) mncf ct(AOa=4 &g=3, 4 B'g )/ct(AOa=4 ) mncf ct(010 &100&110)/ ct(010) mncf 0 / 1 mncf ct(&c C(A)Bc &IC)/ct(&c C(A)Bc) mncf ct(Bc=3 &0011)/ct(Bc=3 ) mncf ct(0101 &0011)/ct(0101 ) mncf 1 / 2 mncf