Project.pptx
- Количество слайдов: 20

Republic of Kazakhstan Ministry of Education and Science Karagandy Regional Specialized Boarding School for Gifted Children “Daryn” Continued fractions and their usage Myrzagul Aigerim Muhammedzhanova Dinargul

Purpose: To study theories of the continued fractions, their use and application, research properties. The actuality: Continued fractions are used in Mathematical theories , and in other natural areas of science such as physics, astronomy , botany , and in such arts as music and architecture. Problems: 1) to study the properties of continued fractions in mathematical theories ( algebra, geometry ). 2 ) Conversion of continued fractions in simple and easy-to-chain; using continued fractions in the derivation of the square root, as well as in solving equations. 3) Determination of the differences and the relationship of simple and continued fractions in astronomy: Julian calendar, the Persian calendar ( calendar Omar Khayyam) Gregorian, Midler and other calendars. 4) Using continued fractions in physics when creating circuits. 5) Using continued fractions in architecture, music and other arts. Novelty: Methods of application of continued fractions in the natural science field were researched.

3 1 Scheme of the continued fractions 2 Convergent fractions 3 Using of continued fractions v Geometry; v Algebra; v Physics; v Astronomy.
Chapter I Finding a square root Scheme of the continued fractions Properties of continued fractions

Scheme of the continued fractions Such fractions as shown here are called “continued fractions”. In such fractions fraction with numerator 1 is added to the number , fraction with numerator 1 is added to the number of that fraction, and fraction with numerator 1 is added to the number of a fraction of that fraction and so on. Here the numbers are whole numbers (number can be equal to 0). Fractions with the meaning in continued fractions are called making fractions. If makers are infinitely many, they are called infinite fractions, and if makers can be counted, they are called finite fractions. The fraction shown above can be written in this form

Theorem 1: Every finite continued fraction can be expressed in a form of common fraction with the value equal to the it. Theorem 2(converse theorem): Every common fraction with positive value can be expressed in a form of continued fraction with the value equal to it. For example:

Convergent fractions If to count some makers from the beginning of the continued fraction, to separate them out and to convert their meaning into a common fraction, consequently the appeared fraction is called a convergent fraction. Theorem 3. In order to find the segment at the place of it is necessary to multiply the segment of the previous convergent n by the appropriate multiple , to add the segment of the fraction at the place to the multiplied one. This way it is necessary to multiply the numerator at the place by the appropriate multiple and to add the numerator of the fraction to the multiplied one. Theorem 4. The value of the finite continued fraction is between values of the neighbouring convergents; and it is closer to the value of the behind convergent rather that to the value of the following one.

Some ways to use the continued fractions Geometry If the numerator and the segment of the given fraction are very large numbers, sometimes it is easier to take fractions with simpler numbers convergent to its real meaning. So it is necessary to change the given fraction for the continued fraction and to use instead of it a value of one of other convergents. For example, if the real value between the circle and its diameter is between the fractions 3, 1415926 and 3, 1415927, if we express the required multiple π (or otherwise pi), to find the values of π easy to write and convergent to the real value, first of all let’s convert the previous fractions into the form of the continued fraction. Then If we take only mutually common multiples of two continued fractions, we will find that π is equal to this fraction:

Finding a square root Let’s take a problem to find a square root of 13. For it let’s use the following project: 1) the greatest square root entering into 13 is 3, because if we take 4, it is 16 and its square power is greater the given number.
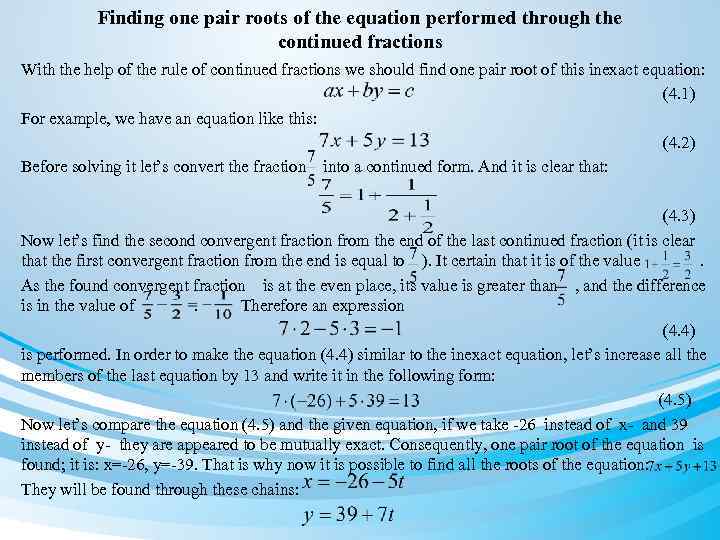
Finding one pair roots of the equation performed through the continued fractions With the help of the rule of continued fractions we should find one pair root of this inexact equation: (4. 1) For example, we have an equation like this: (4. 2) Before solving it let’s convert the fraction into a continued form. And it is clear that: (4. 3) Now let’s find the second convergent fraction from the end of the last continued fraction (it is clear that the first convergent fraction from the end is equal to ). It certain that it is of the value . As the found convergent fraction is at the even place, its value is greater than , and the difference is in the value of . Therefore an expression (4. 4) is performed. In order to make the equation (4. 4) similar to the inexact equation, let’s increase all the members of the last equation by 13 and write it in the following form: (4. 5) Now let’s compare the equation (4. 5) and the given equation, if we take -26 instead of x- and 39 instead of y- they are appeared to be mutually exact. Consequently, one pair root of the equation is found; it is: x=-26, y=-39. That is why now it is possible to find all the roots of the equation: They will be found through these chains:

Chapter II Use of continued fractions in the other sciences Astronomy Botany Continued fractions Music Physics Mechanics

Continued fraction and calendar As we know 1 year 1 = 365 days 5 hours 48 minutes 46 seconds = 365, 242199. . . days. Days are measured as a circadian period and fractions of the sun years conform to its length. It is possible to make a calendar of 365, 242199…=365; 4, 7, 1, 3, 5, …days.

Calendars

Usage in music Since the time of Bach evenly tempered scale containing 12 semitones in each octave is used in music.

Usage in physics. Let’s consider the following examples of the continued fractions usage in physics. The following information is clear to us from the physics textbooks. If we connect resistors with resistance in chain, then the total resistance of the chain will be equal to the number . And if we connect these resistors parallel, then the total resistance will be equal to this number:

Example: It is necessary to make a chain with the resistance . To make this chain we can connect 7 resistors parallel and connect such 10 chains in chain, then the resistance will be . For it we need a resistor . Can we use resistors less than 70 to make a chain with the resistance ? To answer this question we are going to group into continued fractions: For this we make 2 resistors with the resistance equal to 1 and 1 block of 3 resistors connected in chain. Then the resistance of this block will be: And now we connect this block to 1 resistor with the resistance equal to 1 in chain. Then the resistance of the whole chain will be: .

Using of continued fractions in botany


Conclusion Having investigated this topic we get to know one type of the fractions – continued fractions. Due to our scientific project in addition to the continued fractions we learned their features, their convergent fractions, their usage in finding the roots of the equations and the way of converting common fractions into the continued fractions. Also we studied the ways of the usage in mathematics and other natural sciences. Moreover, the role of the continued fractions in making a calendar is great. We have considered in this project accuracy and correlations among the continued fractions of calendars like of Julian, Persian (Omar Khayyam), Gregorian, Midler and also the differences among these calendars. If to consider the usage in physics when using these fractions in making an electric chain, it was found that is possible to save much voltage and some resistors. Also we have given proofs to the usage of the continued fractions in botany, mechanics and architecture. For example, leaves of tree branches are placed in the kind of a spiral or a screw. the spiral was found in the placing of sunflower seeds, pineapple and cactus thorns.

Thanks for your attention
Project.pptx