Representing Meaning Lecture 18 12 Sep 2007

Скачать презентацию Representing Meaning Lecture 18 12 Sep 2007

ec29551f64d91a5dd25fac49cfaf1dd2.ppt

Количество слайдов: 90

Representing Meaning Lecture 18 12 Sep 2007

Transition p p First we did words (morphology) Then simple sequences of words Then we looked at true syntax Now we’re moving on to meaning. Where some would say we should have started to begin with.

Meaning p p Language is useful and amazing because it allows us to encode/decode… n Descriptions of the world n What we’re thinking n What we think about what other people think Don’t be fooled by how natural and easy it is… In particular, you never really… n Utter word strings that match the world n Say what you’re thinking n Say what you think about what other people think

Meaning p You’re simply uttering linear sequences of words such that when other people read/hear and understand them they come to know what you think of the world.

Meaning Representations p p p We’re going to take the same basic approach to meaning that we took to syntax and morphology We’re going to create representations of linguistic inputs that capture the meanings of those inputs. But unlike parse trees and the like these representations aren’t primarily descriptions of the structure of the inputs… In most cases, meaning representations are simultaneously descriptions of the meanings of utterances and of some potential state of affairs in some world.

Introduction p p Meaning representation languages: capturing the meaning of linguistic utterances using formal notation so that they make semantic processing possible Example: deciding what to order at a restaurant by reading a menu, giving advice about where to go for dinner n Requires knowledge about food, its preparation, what people like to eat and what restaurants are like Example: answering a question on an exam n Requires background knowledge about the topic of the question Example: Learning to use a software by reading a manual n Requires knowledge about current computers, the specific software, similar software applications, knowledge about users in general.

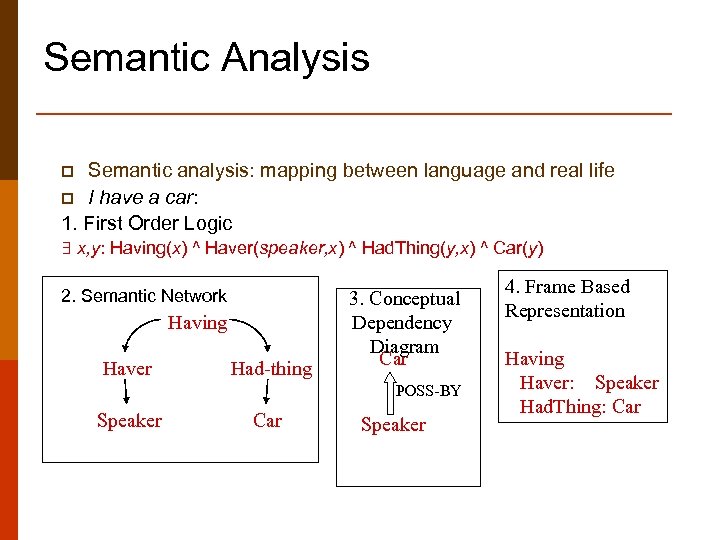Semantic Analysis Semantic analysis: mapping between language and real life p I have a car: 1. First Order Logic p ∃ x, y: Having(x) ^ Haver(speaker, x) ^ Had. Thing(y, x) ^ Car(y) 2. Semantic Network Having Haver Had-thing 3. Conceptual Dependency Diagram Car POSS-BY Speaker Car Speaker 4. Frame Based Representation Having Haver: Speaker Had. Thing: Car

Semantic analysis p A meaning representation consists of structures composed from a set of symbols, or representational vocabulary.

p p Why meaning representations are needed? What they should do for us? Example: Giving advice about restaurants to tourists. A computer system that accepts spoken language queries from tourists and constructs appropriate responses by using a knowledge base of relevant domain knowledge. p Representations that n Permit us to reason about their truth (relationship to some world) n Permit us to answer questions based on their content n Permit us to perform inference (answer questions and determine the truth of things we don’t actually know)

Semantic Processing p Touchstone application is often question answering n Can a machine answer questions involving the meaning of some text or discourse? n What kind of representations do we need to mechanize that process?

Verifiability: Ability to compare the state of affairs described by a representation to the state of affairs in some world modeled in a knowledge base. p Example: Does Anarkali serve vegetarian food? p Knowledge base (KB) Sample entry in KB: Serves(Anarkali, Vegetarian Food) Convert question to logical form and verify its truth value against the knowledge base p p

Unambiguousness p p Example: I want to eat someplace near Chowringhee. (multiple interpretations) Interpretation is important Preferred interpretations Regardless of ambiguity in the input, it is critical that a meaning representation language support representations that have a single unambiguous interpretation.

Vagueness p Vagueness: I want to eat Italian food. - what particular food? p Meaning representation language must support some vagueness

Canonical form Inputs that have the same meaning should have the same meaning representation. Distinct sentences having the same meaning n Does Anarkali have vegetarian dishes? n Do they have vegetarian food at Anarkali? n Are vegetarian dishes served at Anarkali? n Does Anarkali serve vegetarian fare? p Words have different senses, multiple words may have the same sense n Having vs. serving n Food vs. fare vs. dishes (each is ambiguous but one sense of each matches the others) p Alternative syntactic analyses have related meaning (Ex: active vs passive)

Inference and variables; expressiveness p p Inference and variables: n Can vegetarians eat at Anarkali? n I’d like to find a restaurant that serves vegetarian food. n Serves (x, Vegetarian. Food) n System’s ability to draw valid conclusions based on the meaning representations of inputs and its store of background knowledge. Expressiveness: n system must be able to handle a wide range of subject matter

Semantic Processing p We’re going to discuss 2 ways to attack this problem (just as we did with parsing) n There’s theoretically motivated correct and complete approach… p n Computational/Compositional Semantics And there are practical approaches that have some hope of being useful and successful. p Information extraction

Meaning Structure of Language p The various methods by which human languages convey meaning n Form-meaning associations n Word-order regularities n Tense systems n Conjunctions n Quantifiers n A fundamental predicate-argument structure p p Asserts that specific relationships / dependencies hold among the concepts underlying the constituent words and phrases The underlying structure permits the creation of a single composite meaning representation from the meanings of the various parts.

Predicate-argument structure Sentences Syntactic argument frames I want Italian food. NP want NP I want to spend less than five dollars. NP want Inf-VP I want it to be close by here. NP want NP Inf-VP The syntactic frames specify the number, position and syntactic category of the arguments that are expected to accompany a verb. p p Thematic roles: e. g. entity doing the wanting vs. entity that is wanted (linking surface arguments with the semantic=case roles) Syntactic selection restrictions: I found to fly to Dallas. Semantic selection restrictions: The risotto wanted to spend less than ten dollars. Make a reservation for this evening for a table for two persons at eight: Reservation (Hearer, Today, 8 PM, 2)

p Any useful meaning representation language must be organized in a way that supports the specification of semantic predicate-argument structures. n Variable arity predicate-argument structures n The semantic labeling of arguments to predicates n The statement of semantic constraints on the fillers of argument roles

Model-theoretic semantics p Basic notions shared by representation schemes Ability to represent Objects p Properties of objects p Relations among objects p p p A model is a formal construct that stands for the particular state of affairs in the world that we are trying to represent. Expressions in a meaning representation language will be mapped in a systematic way to the elements of the model.

p Vocabulary of a meaning representation language n n p Non-logical vocabulary: open-ended set of names for the objects, properties and relations (may appear as predicates, nodes, labels on links, labels in slots in frames, etc) Logical vocabulary: closed set of symbols, operators, quantifiers, links, etc. provide the formal meaning for composing expressions Each element of non-logical vocabulary must have a denotation in the model. n n n domain of a model: set of objects that are part of the application Capture properties of objects by a set (of domain elements having the property) Relations denote sets of tuples of elements on the domain

p Interpretation: a mapping that maps from the nonlogical vocabulary of our meaning representation to the corresponding denotations in the model.

Representational Schemes p We’re going to make use of First Order Predicate Calculus (FOPC) as our representational framework n Not because we think it’s perfect n All the alternatives turn out to be either too limiting or n They turn out to be notational variants

FOPC p Allows for… n The analysis of truth conditions p n Supports the use of variables p n Allows us to answer yes/no questions Allows us to answer questions through the use of variable binding Supports inference p Allows us to answer questions that go beyond what we know explicitly

FOPC p p p This choice isn’t completely arbitrary or driven by the needs of practical applications FOPC reflects the semantics of natural languages because it was designed that way by human beings In particular…

Example p I only have five dollars and I don’t have a lot of time. p p Have(Speaker, Five. Dollars) ∧ ¬ Have(Speaker, Lot. Of. Time) variables: n Have(x, Five. Dollars) ∧ ¬ Have(x, Lot. Of. Time) p Note: grammar is recursive

Semantics of FOPC p p p FOPC sentences can be assigned a value of true or false. Anarkali is near RC. Near (Location. Of (Anarkali), Location. Of (RC))

Inference p Modus ponens: ⇒ p Example: Vegetarian. Restaurant(Joe’s) x: Vegetarian. Restaurant(x) ⇒ Serves(x, Vegetarian. Food) Serves(Joe’s, Vegetarian. Food)

Uses of modus ponens p p p Forward chaining: as individual facts are added to the database, all derived inferences are generated Backward chaining: starts from queries. Example: the Prolog programming language father(X, Y) : - parent(X, Y), male(X). parent(john, bill). parent(jane, bill). female(jane). male (john). ? - father(M, bill).

Variables and quantifiers p A restaurant that serves Mexican food near UM. p ∃ p All vegetarian restaurants serve vegetarian food. p x: Vegetarian. Restaurant(x) x: Restaurant(x) ∧ Serves(x, Mexican. Food) ∧ Near(Location. Of(x), Location. Of(UM)) ⇒ Serves (x, Vegetarian. Food) p If this sentence is true, it is also true for any substitution of x. However, if the condition is false, the sentence is always true.

Meaning Structure of Language p The semantics of human languages… n Display a basic predicate-argument structure n Make use of variables n Make use of quantifiers n Use a partially compositional semantics

Predicate-Argument Structure p p Events, actions and relationships can be captured with representations that consist of predicates and arguments to those predicates. Languages display a division of labor where some words and constituents function as predicates and some as arguments.

Predicate-Argument Structure p p Predicates n Primarily Verbs, VPs, PPs, Sentences n Sometimes Nouns and NPs Arguments n Primarily Nouns, Nominals, NPs, PPs n But also everything else; as we’ll see it depends on the context

Example p p p Mary gave a list to John. Giving(Mary, John, List) More precisely n Gave conveys a three-argument predicate n The first arg is the subject n The second is the recipient, which is conveyed by the NP in the PP n The third argument is the thing given, conveyed by the direct object

Not exactly The statement n The first arg is the subject can’t be right. p Subjects can’t be givers. p We mean that the meaning underlying the subject phrase plays the role of the giver. p

Better p p Turns out this representation isn’t quite as useful as it could be. n Giving(Mary, John, List) Better would be

Predicates p p p The notion of a predicate just got more complicated… In this example, think of the verb/VP providing a template like the following The semantics of the NPs and the PPs in the sentence plug into the slots provided in the template

Compositional Semantics p Compositional Semantics n Syntax-driven methods of assigning semantics to sentences

Semantic Analysis p Semantic analysis is the process of taking in some linguistic input and assigning a meaning representation to it. n There a lot of different ways to do this that make more or less (or no) use of syntax n We’re going to start with the idea that syntax does matter p The compositional rule-to-rule approach

Semantic Processing p We’re going to discuss 2 ways to attack this problem (just as we did with parsing) n There’s theoretically motivated correct and complete approach… p n Computational/Compositional Semantics Create a FOL representation that accounts for all the entities, roles and relations present in a sentence. And there are practical approaches that have some hope of being useful and successful. p Information extraction Do a superficial analysis that pulls out only the entities, relations and roles that are of interest to the consuming application.

Compositional Analysis p p p Principle of Compositionality n The meaning of a whole is derived from the meanings of the parts What parts? n The constituents of the syntactic parse of the input What could it mean for a part to have a meaning?

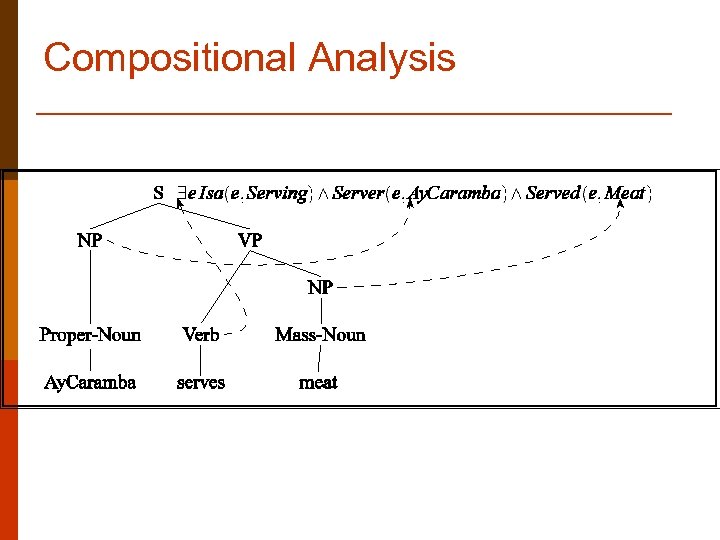
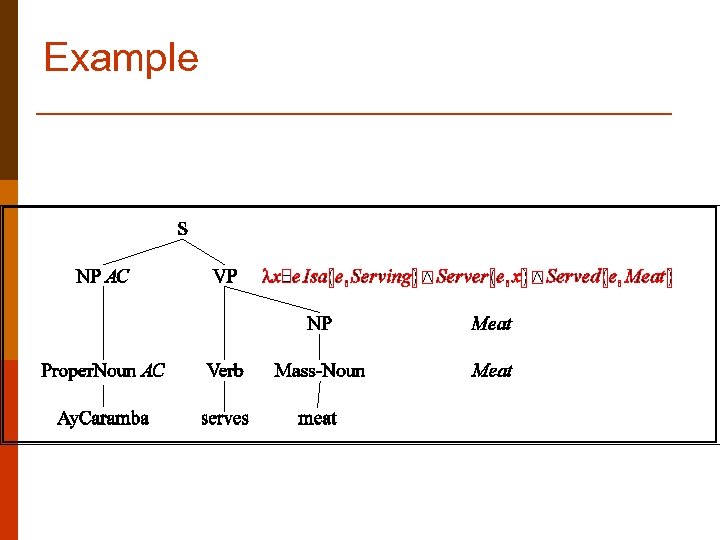
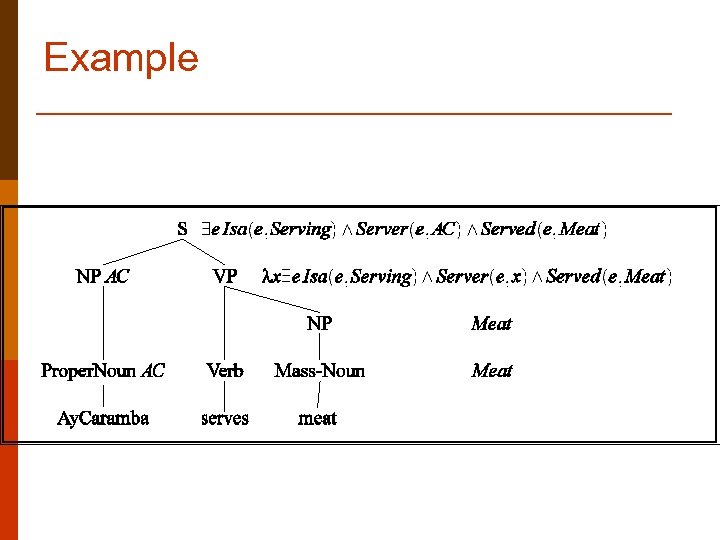
Example p Ay. Caramba serves meat

Compositional Analysis

Augmented Rules p p p We’ll accomplish this by attaching semantic formation rules to our syntactic CFG rules Abstractly This should be read as the semantics we attach to A can be computed from some function applied to the semantics of A’s parts.

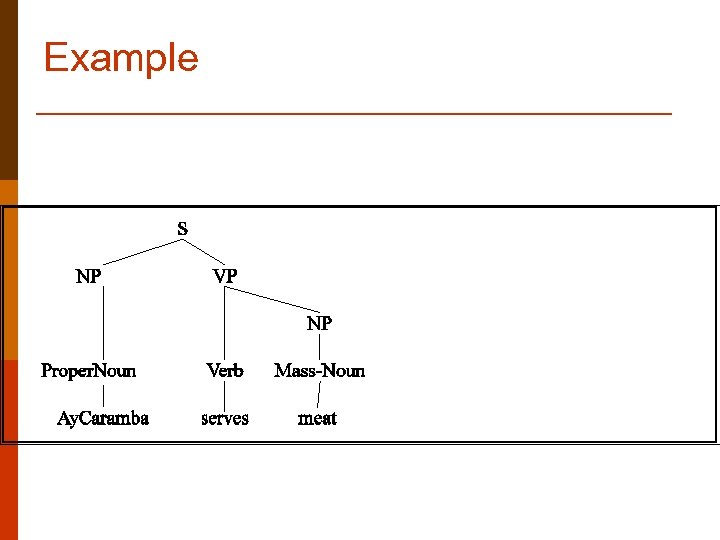
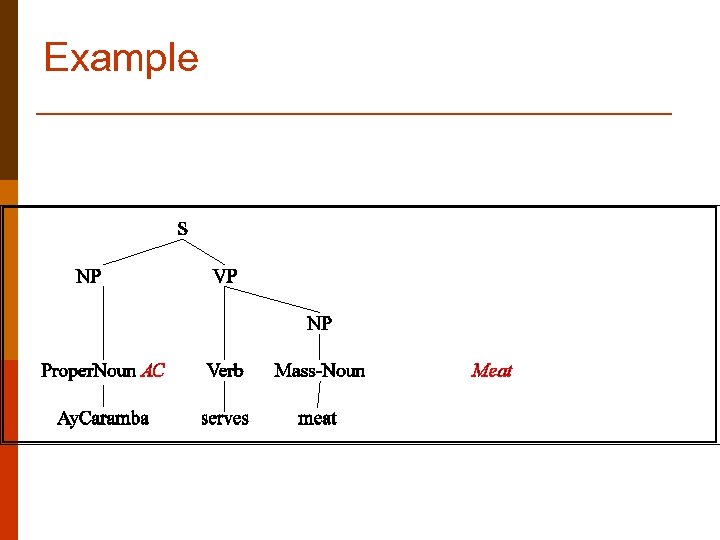
Example p Easy parts… n n NP -> Prop. Noun NP -> Mass. Noun Prop. Noun -> Ay. Caramba Mass. Moun -> meat p Attachments {Prop. Noun. sem} {Mass. Noun. sem} {Ay. Caramba} {MEAT}

Example p p p S -> NP VP VP -> Verb NP Verb -> serves p p p {VP. sem(NP. sem)} {Verb. sem(NP. sem) ? ? ?

Lambda Forms p A simple addition to FOPC n Take a FOPC sentence with variables in it that are to be bound. n Allow those variables to be bound by treating the lambda form as a function with formal arguments

Example Example

Syntax/Semantics Interface: Two Philosophies 1. 2. Let the syntax do what syntax does well and don’t expect it to know much about meaning n In this approach, the lexical entry’s semantic attachments do all the work Assume the syntax does know something about meaning • Here the grammar gets complicated and the lexicon simpler (constructional approach)

Example p Mary freebled John the nim. p Who has it? p Where did he get it from? p Why?

Example p Consider the attachments for the VPs VP -> Verb NP NP rule (gave Mary a book) VP -> Verb NP PP (gave a book to Mary) Assume the meaning representations should be the same for both. Under the lexicon-heavy scheme, the VP attachments are: VP. Sem (NP. Sem, NP. Sem) VP. Sem (NP. Sem, PP. Sem)

Example p p Under a syntax-heavy scheme we might want to do something like VP -> V NP NP V. sem ^ Recip(NP 1. sem) ^ Object(NP 2. sem) VP -> V NP PP V. Sem ^ Recip(PP. Sem) ^ Object(NP 1. sem) i. e the verb only contributes the predicate, the grammar “knows” the roles.

Integration p Two basic approaches n Integrate semantic analysis into the parser (assign meaning representations as constituents are completed) n Pipeline… assign meaning representations to complete trees only after they’re completed

Example p p From BERP n I want to eat someplace near campus Two parse trees, two meanings

Pros and Cons p If you integrate semantic analysis into the parser as it is running… n You can use semantic constraints to cut off parses that make no sense n But you assign meaning representations to constituents that don’t take part in the correct (most probable) parse

Mismatches p p There are unfortunately some annoying mismatches between the syntax of FOPC and the syntax provided by our grammars… So we’ll accept that we can’t always directly create valid logical forms in a strictly compositional way n We’ll get as close as we can and patch things up after the fact.

Complex Terms p Allow the compositional system to pass around representations like the following as objects with parts: Complex-Term →

Example p Our restaurant example winds up looking like p Big improvement…

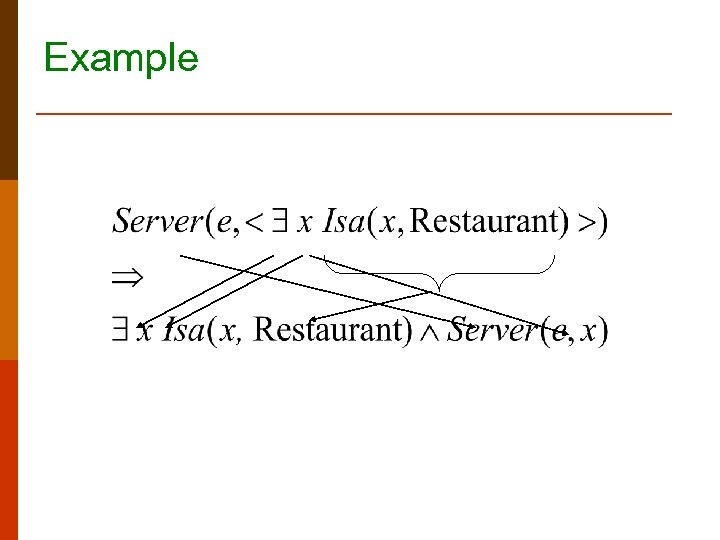
Conversion p So… complex terms wind up being embedded inside predicates. So pull them out and redistribute the parts in the right way… P() turns into Quantifier var body connective P(var)

Example Example

Quantifiers and Connectives p If the quantifier is an existential, then the connective is an ^ (and) p If the quantifier is a universal, then the connective is an > (implies)

Multiple Complex Terms p p Note that the conversion technique pulls the quantifiers out to the front of the logical form… That leads to ambiguity if there’s more than one complex term in a sentence.

Quantifier Ambiguity p Consider n Every restaurant has a menu n n That could mean that every restaurant has a menu Or that There’s some uber-menu out there and all restaurants have that menu

Quantifier Scope Ambiguity

Ambiguity p p p This turns out to be a lot like the prepositional phrase attachment problem The number of possible interpretations goes up exponentially with the number of complex terms in the sentence The best we can do is to come up with weak methods to prefer one interpretation over another

Non-Compositionality p Unfortunately, there are lots of examples where the meaning (loosely defined) can’t be derived from the meanings of the parts n Idioms, jokes, irony, sarcasm, metaphor, metonymy, indirect requests, etc

English Idioms p p Kick the bucket, buy the farm, bite the bullet, run the show, bury the hatchet, etc… Lots of these… constructions where the meaning of the whole is either n Totally unrelated to the meanings of the parts (kick the bucket) n Related in some opaque way (run the show)

The Tip of the Iceberg p Describe this construction 1. A fixed phrase with a particular meaning 2. A syntactically and lexically flexible phrase with a particular meaning 3. A syntactically and lexically flexible phrase with a partially compositional meaning 4. …

Example p p p Enron is the tip of the iceberg. NP -> “the tip of the iceberg” Not so good… attested examples… n the tip of Mrs. Ford’s iceberg n the tip of a 1000 -page iceberg n the merest tip of the iceberg How about n That’s just the iceberg’s tip.

Example p p What we seem to need is something like NP -> An initial NP with tip as its head followed by a subsequent PP with of as its head and that has iceberg as the head of its NP And that allows modifiers like merest, Mrs. Ford, and 1000 -page to modify the relevant semantic forms

Quantified Phrases p Consider A restaurant serves meat. Assume that A restaurant looks like p If we do the normal lambda thing we get p

END END

Examples from Russell&Norvig (1) p 7. 2. p. 213 p Not all students take both History and Biology. Only one student failed History. Only one student failed both History and Biology. The best history in History was better than the best score in Biology. Every person who dislikes all vegetarians is smart. No person likes a smart vegetarian. There is a woman who likes all men who are vegetarian. There is a barber who shaves all men in town who don't shave themselves. No person likes a professor unless a professor is smart. Politicians can fool some people all of the time or all people some of the time but they cannot fool all people all of the time. p p p p p

Categories & Events p p Categories: n Vegetarian. Restaurant (Joe’s) – categories are relations and not objects n Most. Popular(Joe’s, Vegetarian. Restaurant) – not FOPC! n ISA (Joe’s, Vegetarian. Restaurant) – reification (turn all concepts into objects) n AKO (Vegetarian. Restaurant, Restaurant) Events: n Reservation (Hearer, Joe’s, Today, 8 PM, 2) n Problems: p p Determining the correct number of roles Representing facts about the roles associated with an event Ensuring that all the correct inferences can be drawn Ensuring that no incorrect inferences can be drawn

MUC-4 Example On October 30, 1989, one civilian was killed in a reported FMLN attack in El Salvador. INCIDENT: DATE INCIDENT: LOCATION INCIDENT: TYPE INCIDENT: STAGE OF EXECUTION INCIDENT: INSTRUMENT ID INCIDENT: INSTRUMENT TYPE PERP: INCIDENT CATEGORY PERP: INDIVIDUAL ID PERP: ORGANIZATION ID PERP: ORG. CONFIDENCE PHYS TGT: ID PHYS TGT: TYPE PHYS TGT: NUMBER PHYS TGT: FOREIGN NATION PHYS TGT: EFFECT OF INCIDENT PHYS TGT: TOTAL NUMBER HUM TGT: NAME HUM TGT: DESCRIPTION HUM TGT: TYPE HUM TGT: NUMBER HUM TGT: FOREIGN NATION HUM TGT: EFFECT OF INCIDENT HUM TGT: TOTAL NUMBER 30 OCT 89 EL SALVADOR ATTACK ACCOMPLISHED TERRORIST ACT "TERRORIST" "THE FMLN" REPORTED: "THE FMLN" "1 CIVILIAN" CIVILIAN: "1 CIVILIAN" 1: "1 CIVILIAN" DEATH: "1 CIVILIAN"

Subcategorization frames 1. 2. 3. 4. 5. 6. 7. I ate a turkey sandwich at my desk I ate lunch I ate a turkey sandwich for lunch at my desk - no fixed “arity” (problem for FOPC)

One possible solution Eating 1 (Speaker) 2. Eating 2 (Speaker, Turkey. Sandwich) 3. Eating 3 (Speaker, Turkey. Sandwich, Desk) 4. Eating 4 (Speaker, Desk) 5. Eating 5 (Speaker, Lunch) 6. Eating 6 (Speaker, Turkey. Sandwich, Lunch) 7. Eating 7 (Speaker, Turkey. Sandwich, Lunch, Desk) Meaning postulates are used to tie semantics of predicates: w, x, y, z: Eating 7(w, x, y, z) ⇒ Eating 6(w, x, y) Scalability issues again! 1.

Another solution - Say that everything is a special case of Eating 7 with some arguments unspecified: ∃w, x, y Eating (Speaker, w, x, y) - Two problems again: Too many commitments (e. g. , no eating except at meals: lunch, dinner, etc. ) No way to individuate events: ∃w, x Eating (Speaker, w, x, Desk) ∃w, y Eating (Speaker, w, Lunch, y) – cannot combine into ∃w Eating (Speaker, w, Lunch, Desk)

Reification p p w: Isa(w, Eating) ∧ Eater(w, Speaker) ∧ Eaten(w, Turkey. Sandwich) – equivalent to sentence 5. Reification: n No need to specify fixed number of arguments for a given surface predicate n No more roles are postulated than mentioned in the input n No need for meaning postulates to specify logical connections among closely related examples ∃

Representing time 3. I arrived in New York I am arriving in New York I will arrive in New York p ∃ 1. 2. w: Isa(w, Arriving) ∧ Arriver(w, Speaker) ∧ Destination(w, New. York)

Representing time p p p i, e, w, t: Isa(w, Arriving) ∧ Arriver(w, Speaker) ∧ Destination(w, New. York) ∧ Interval. Of(w, i) ∧ End. Point(I, e) ∧ Precedes (e, Now) ∃ i, e, w, t: Isa(w, Arriving) ∧ Arriver(w, Speaker) ∧ Destination(w, New. York) ∧ Interval. Of(w, i) ∧ Member. Of(i, Now) ∃ i, e, w, t: Isa(w, Arriving) ∧ Arriver(w, Speaker) ∧ Destination(w, New. York) ∧ Interval. Of(w, i) ∧ Start. Point(i, s) ∧ Precedes (Now, s) ∃

Representing time p p p We fly from San Francisco to Boston at 10. Flight 1390 will be at the gate an hour now. n Use of tenses Flight 1902 arrived late. Flight 1902 had arrived late. n “similar” tenses When Mary’s flight departed, I ate lunch When Mary’s flight departed, I had eaten lunch n reference point

Aspect p p p Stative: I know my departure gate Activity: John is flying no particular end point Accomplishment: Sally booked her flight natural end point and result in a particular state Achievement: She found her gate Figuring out statives: * I am needing the cheapest fare. * I am wanting to go today. * Need the cheapest fare!

Representing beliefs p p Want, believe, imagine, know - all introduce hypothetical worlds I believe that Mary ate British food. Reified example: n ∃ u, v: Isa(u, Believing) ∧ Isa(v, Eating) ∧ Believer (u, Speaker) ∧ Believed. Prop(u, v) ∧ Eater(v, Mary) ∧ Eaten(v, British. Food) However this implies also: n ∃ u, v: Isa(v, Eating) ∧ Eater(v, Mary) ∧ Eaten(v, British. Food) Modal operators: n Believing(Speaker, Eating(Mary, British. Food)) - not FOPC! – predicates in FOPC hold between objects, not between relations. n Believes(Speaker, ∃ v: ISA(v, Eating) ∧ Eater(v, Mary) ∧ Eaten(v, British. Food))

Modal operators p p Beliefs Knowledge Assertions Issues: If you are interested in baseball, the Red Sox are playing tonight.

Examples from Russell&Norvig (2) p 7. 3. p. 214 p One more outburst like that and you'll be in comptempt of court. Annie Hall is on TV tonight if you are interested. Either the Red Sox win or I am out ten dollars. The special this morning is ham and eggs. Maybe I will come to the party and maybe I won't. Well, I like Sandy and I don't like Sandy. p p p