Representations of Locations and Patterns Topics of Discussion

Representations of Locations and Patterns Topics of Discussion The physical effects of rotation The geographical use of rotation Latitude and longitude The geographic grid Global time Map Projections

The Geographical Use of Rotation Earth's rotation provides a reference system for location. The earth rotates around two fixed points: • North Pole • South Pole Rotation and Latitude Halfway between the poles, the equator divides the earth into two equal hemispheres. Lines north and south of the equator are parallels. Parallels are lines of latitude. Latitude is measured at an angle from the center of the earth, north and south of the equator.

The first Lines of Parallels and Meridians Eratosthenes 270 - 195 B. C.

LATITUDE AND LONGITUDE Lines of Parallel equate to Latitude is measured from the Equator (00) to the Poles (900 N/S) Lines of Meridians equate to Longitude is measured from the Prime Meridian (00) to the International Date Line (1800 E/W) Both Latitudes and Longitudes are measured in angular distance from the center of the earth

MEASURING LATITUDE • The Equator is a Great Circle: dividing the earth into two equal halves • The Lines of Latitude are measured in angular degrees (°) from the center of the earth, North and South of the Equator • Lines of Latitude are parallel and evenly spaced (hence, Parallels of Latitude): a degree of latitude represents a constant distance on the ground -- Approximately 69 miles (111 km) • Special Parallels: Tropic of Cancer (23 1/2° N), Tropic of Capricorn (23 1/2° S), Arctic Circle (66 1/2° N), and Antarctic Circle (66 1/2° S)

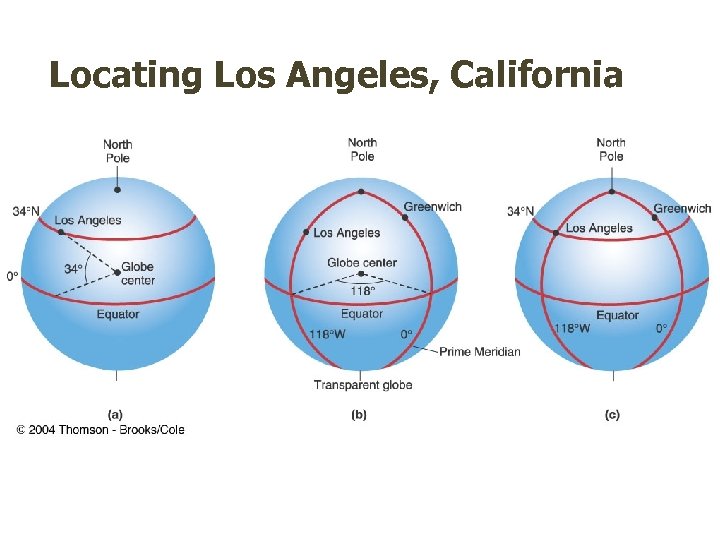Locating Los Angeles, California

Meridians or Longitude Lines drawn from pole to pole are called meridians or lines of longitude. Longitude measures points east and west of the Prime Meridian. The prime meridian passes through Greenwich, England.

MEASURING LONGITUDE • Lines of longitude or meridians are non-parallel circular arcs that converge at the poles • At the equator, a degree of longitude measures about 69 miles (111 km), at 400 N or S, 53 miles (85 km), and at the poles, 0 miles (0 km) • There are 180° of longitude on either side of the Prime Meridian – which is 0°, and starts at the Royal Observatory at Greenwich, London • Each Degree of Latitude and Longitude is subdivided into Minutes (’), and Seconds (”) • Sextants, and Chronometers are used to measure latitudes and longitudes – now increasingly GPS

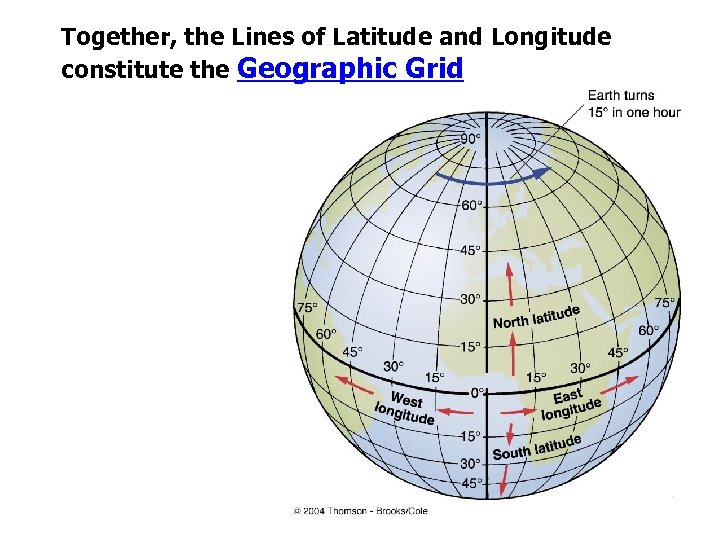Together, the Lines of Latitude and Longitude constitute the Geographic Grid

Geographic Grid Together, latitude and longitude form a geographic grid. Latitude and longitude can be used to define precise locations on earth. Absolute Location The absolute location of San Francisco is latitude 37º 45"N and longitude 122º 26"W.

Rotation Earth rotates on its imaginary axis like a top. The earth rotates from west to east. Each rotation defines a solar day - 24 hours. What are the physical affects of earth’s rotation? 1. Daily Cycle of Night and Day

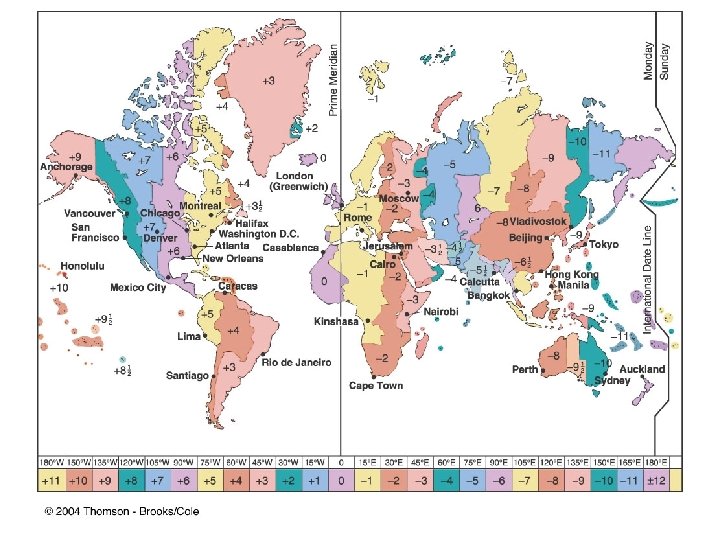
Longitude, Rotation and Time: • Before 1884, “Local Time” based on Solar Noon • Now, we have Time Zones – Why? • In 1884, International Meridian Conference in Washington, D. C. established: a) Prime Meridian (through Greenwich) – GMT and Universal Time Coordinated (UTC) or Zulu Time b) Time Zones – 24 Zones, 15 Degrees or 1 Hour apart, 7. 5 Degrees East & West of the Central Meridian of respective zones (Figure 2. 9)

Global Time What time is it on earth? Global time is Solar time Solar noon - the sun’s highest point in the sky Standard time is a device to improve global timekeeping. The world is divided into 24 time zones. Each time zone is based upon standard meridians at 15° intervals from the prime meridian.

International Date Line The International Date Line is the 180º meridian. Crossing the date line requires adjusting your calendar as well as your watch. You lose a day going west and gain a day going east.

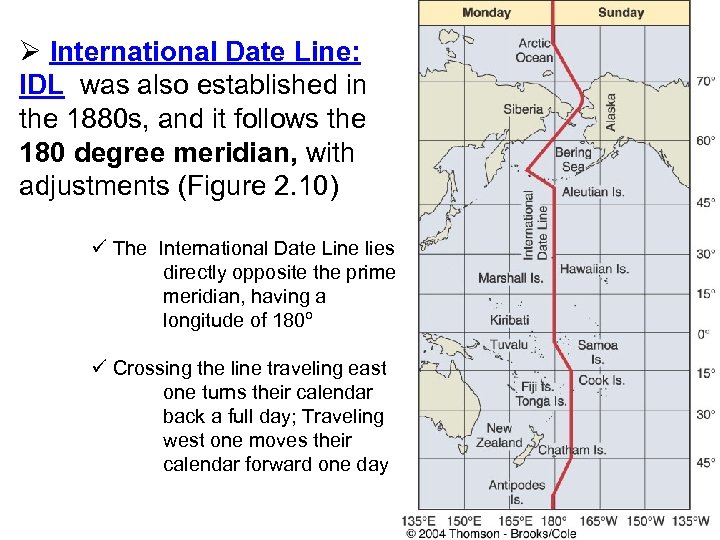Ø International Date Line: IDL was also established in the 1880 s, and it follows the 180 degree meridian, with adjustments (Figure 2. 10) ü The International Date Line lies directly opposite the prime meridian, having a longitude of 180º ü Crossing the line traveling east one turns their calendar back a full day; Traveling west one moves their calendar forward one day

How do you Represent Locations, Places and Patterns of Earth? • Being able to convey (or communicate) where things are, is essential to describing and analyzing aspects of Physical Geography. • A Map is essentially a communication device • Communicates spatial data/information through “graphic symbols” – a language of location (Appendix B)

Emergence of Cartography – the art and science of mapmaking – increasingly an automated, computerized process Ø However, Maps and Mapmaking have evolved over the years, becoming increasingly more complex, sophisticated, automated, and ubiquitous Ø The challenge has always been to represent locations and patterns on earth accurately and efficiently

Maps have been in existence since time immemorial – simple maps of relative locations Very Early Map Town Plan from Catal Hyük, Anatolia, Turkey, 6200 B. C.

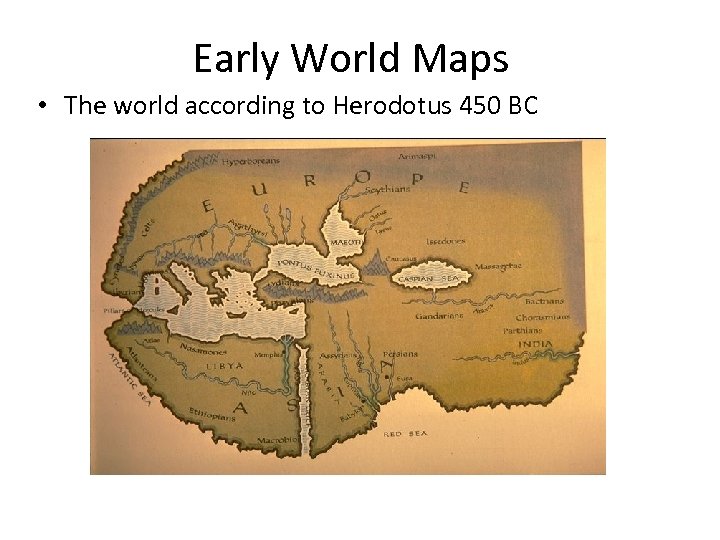Early World Maps • The world according to Herodotus 450 BC

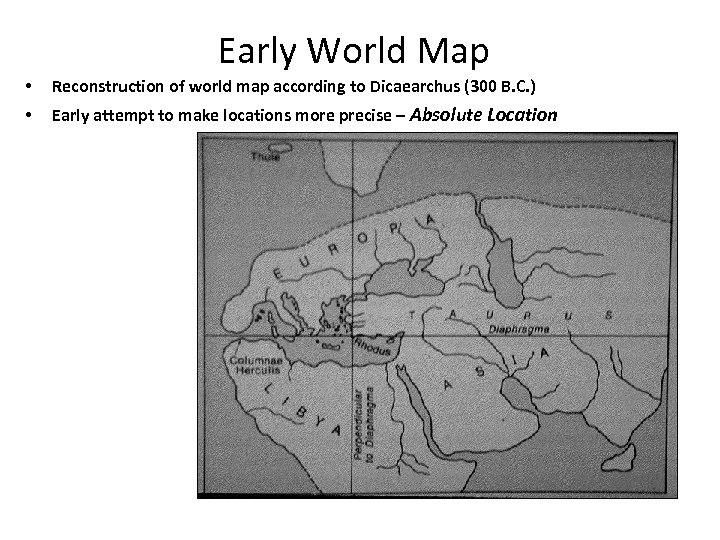Early World Map • Reconstruction of world map according to Dicaearchus (300 B. C. ) • Early attempt to make locations more precise – Absolute Location

Map Projections The challenge is to transfer a spherical grid (or the Geographic Grid) onto a flat surface

Maps and Projections 1. Geographers and other disciplines use a variety of tools that help describe the cultural and physical features on the Earth's surface. 2. A globe shows the earth in 3 D. 3. A map is a two-dimensional representation. 4. The science of map making is Cartography. 5. Maps can be two general types: reference maps and thematic maps. 6. Reference maps show basic locational information such as roads, cities, and rivers. Examples include topographic maps and Google maps. 1. Thematic maps show the distribution of specific geographical information such as weather map or population.

Projections – Going from a Sphere to Flat Maps v Projections are created by transferring points on the earth onto a flat surface. It is like having a light in the center of the earth, shining through the earth’s surface, onto the projection surface v There are three basic methods for doing this: § Cylindrical – projection surface wrapped around the Earth; point of contact is equator § Planar – (or Polar or Zenithal) – projection surface is a ‘flat’ surface against the Earth at a particular latitude or longitude § Conic (or Conical) – projection surface is a cone is placed on or through the surface of the Earth – Where the projection surface touches the earth is the “Standard Line” or “Standard Parallel” Ø Projections now developed mathematically, using computers

Projection Challenges q Distortion – It is impossible to flatten a spherical object without some distortion in its basic attributes or properties q Map Projections try to preserve one or more of the following properties: § Area – relative representation of area size on map (for small areas) Projections that preserve ‘area’ are “Equal Area” projections § Shape – usually referred to as “conformality”, again for small sections Projections that preserve “shape” are “Conformal” § Direction – or “azimuthality” – cardinal directions (N, S, E, W) Projections that preserve “direction” are “Azimuthal” § Distance – variation in distance or scale on the same map Projections that preserve “distance” are “Equidistant” ü CONFORMAL vs. EQUAL AREA: Projections can be either conformal or area – but not both! equal

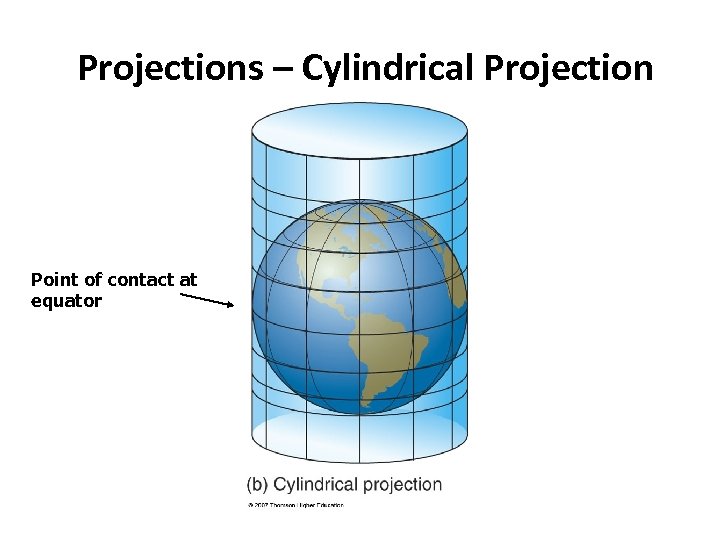Projections – Cylindrical Projection Point of contact at equator

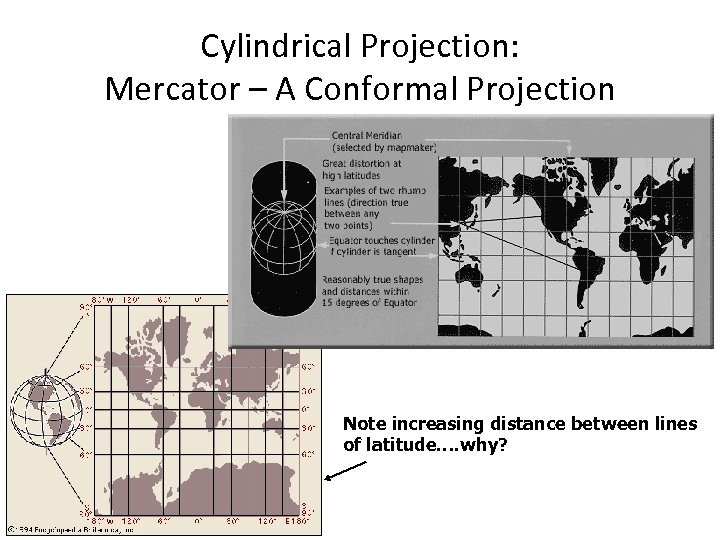Cylindrical Projection: Mercator – A Conformal Projection Note increasing distance between lines of latitude…. why?

Why Mercator? NAVIGATION! • In a Mercator projection, the lines of longitude are straight vertical lines equidistance apart at all latitudes, and horizontal distances are stretched above and below the equator – more toward the poles • The Mercator projection mathematically stretches vertical distances by the same proportion as the horizontal distances so that shape and direction are preserved • Mercator’s projection preserves what sailors in the 16 th century needed – shapes and directions; they were willing to accept size distortion • Any straight line drawn between two points on a Mercator Projection represents a “rhumb line” – true compass direction

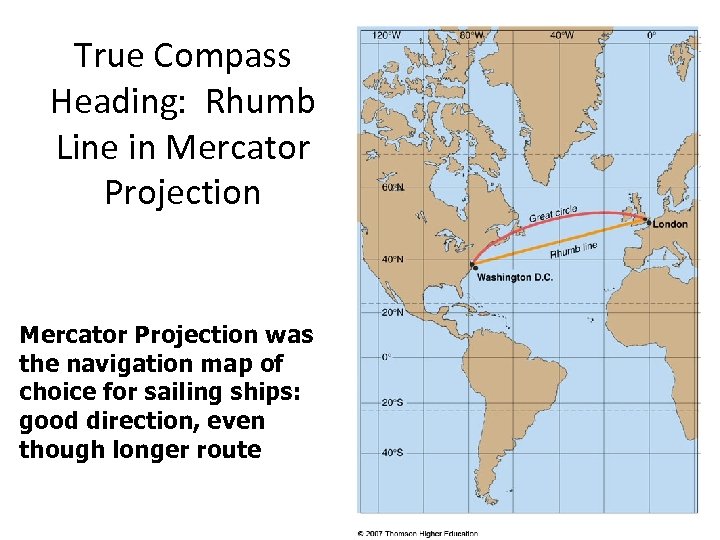True Compass Heading: Rhumb Line in Mercator Projection was the navigation map of choice for sailing ships: good direction, even though longer route

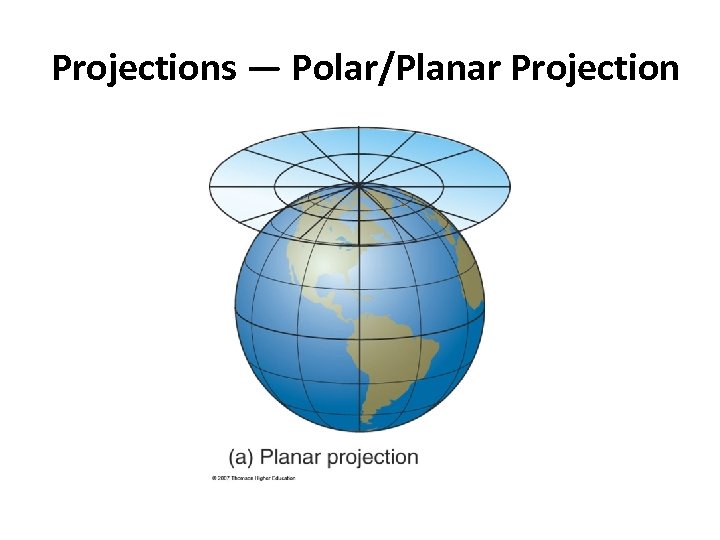Projections — Polar/Planar Projection

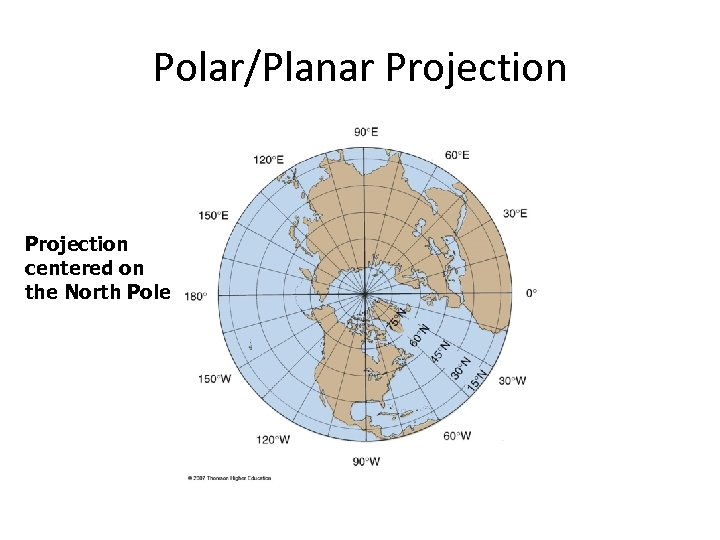Polar/Planar Projection centered on the North Pole

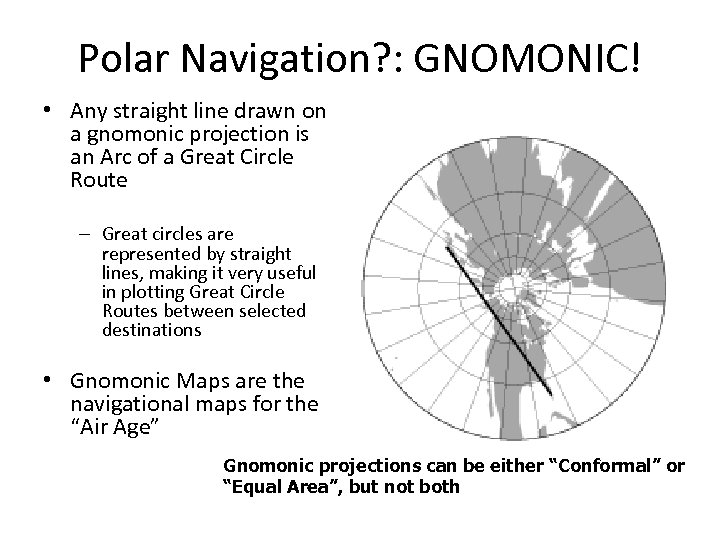Polar Navigation? : GNOMONIC! • Any straight line drawn on a gnomonic projection is an Arc of a Great Circle Route – Great circles are represented by straight lines, making it very useful in plotting Great Circle Routes between selected destinations • Gnomonic Maps are the navigational maps for the “Air Age” Gnomonic projections can be either “Conformal” or “Equal Area”, but not both

Projections — Conic Projection

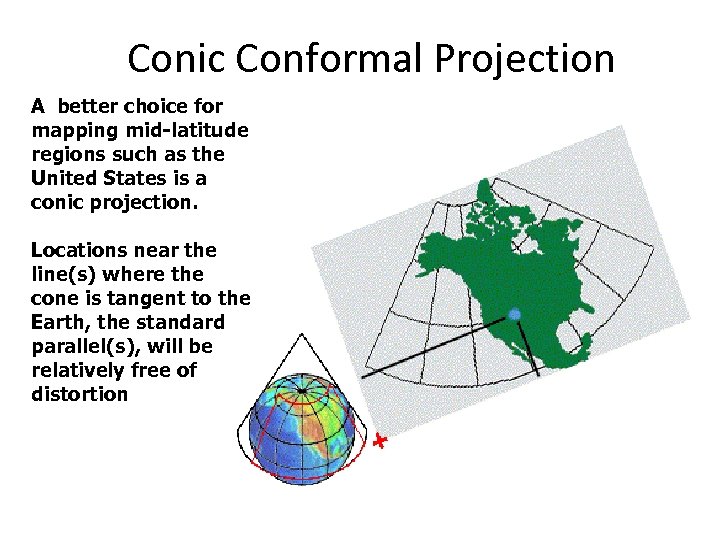Conic Conformal Projection A better choice for mapping mid-latitude regions such as the United States is a conic projection. Locations near the line(s) where the cone is tangent to the Earth, the standard parallel(s), will be relatively free of distortion

Compromise Projections The Robinson Projection is among the compromise projections that uses tabular coordinates rather than mathematical formulas to make earth features look the "right" size and shape. A better balance of size and shape results in a more accurate picture of high-latitude lands like Russia and Canada. Greenland is also truer to size but compressed. It was adopted by the NGS in 1988. http: //www. youtube. com/watch? v=AI 36 MWAH 54 s

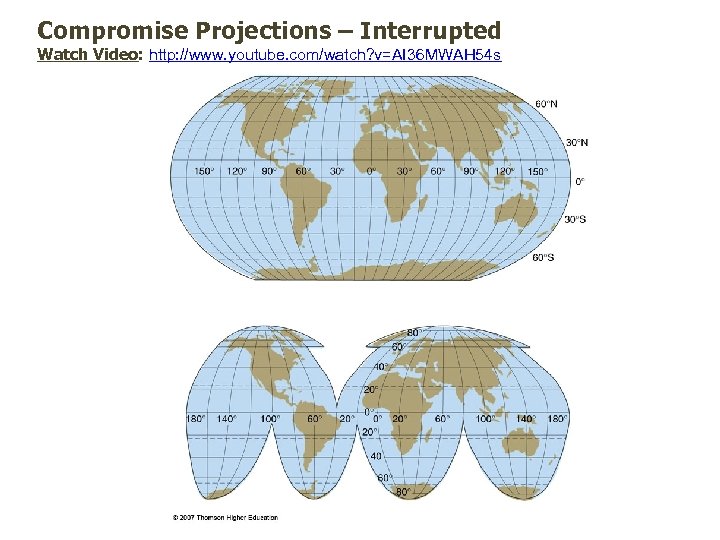Compromise Projections – Interrupted Watch Video: http: //www. youtube. com/watch? v=AI 36 MWAH 54 s

MAP SCALE • Map scale is the ratio of the distance between two points on the Earth’s surface and the distance between corresponding points on a map • There are several types of map scales: • Verbal Scale: 1 inch = 1 mile • Bar Scale: a graph depicting distances • Representative Fraction: One unit of measured distance on a map equal some units of measured distance in the real world – 1: 63360

LARGE-SCALE vs. SMALL-SCALE • Large-Scale Maps show very small portions of the real world, but with great detail – Large-Scale maps have small denominators i. e. , 1: 12, 000 or 1: 24, 000 – Topographic maps are examples of large-scale maps • Small-Scale maps show very large portions of the real world, but with minimal detail – Small-scale maps have large denominators, i. e. , 1: 100, 000 or 1: 1, 000 – Wall maps are examples of small-scale maps

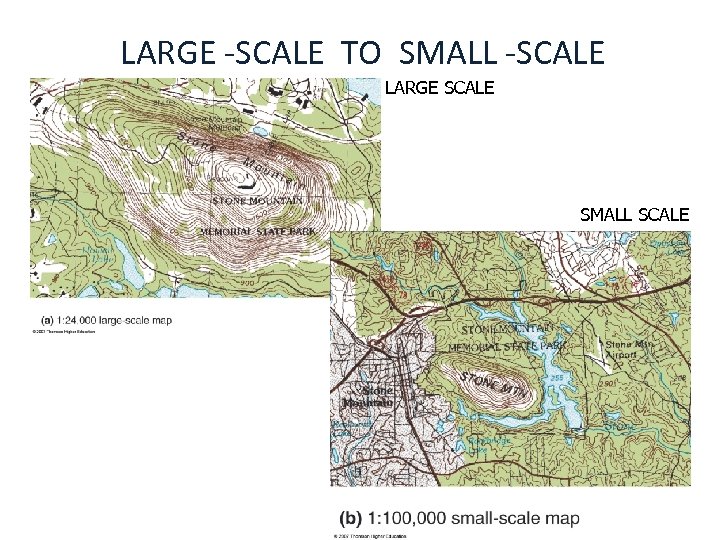LARGE -SCALE TO SMALL -SCALE LARGE SCALE SMALL SCALE

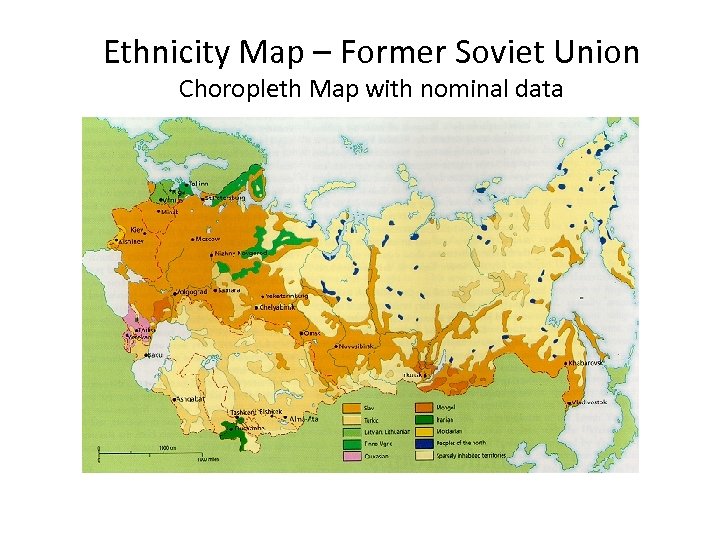Ethnicity Map – Former Soviet Union Choropleth Map with nominal data

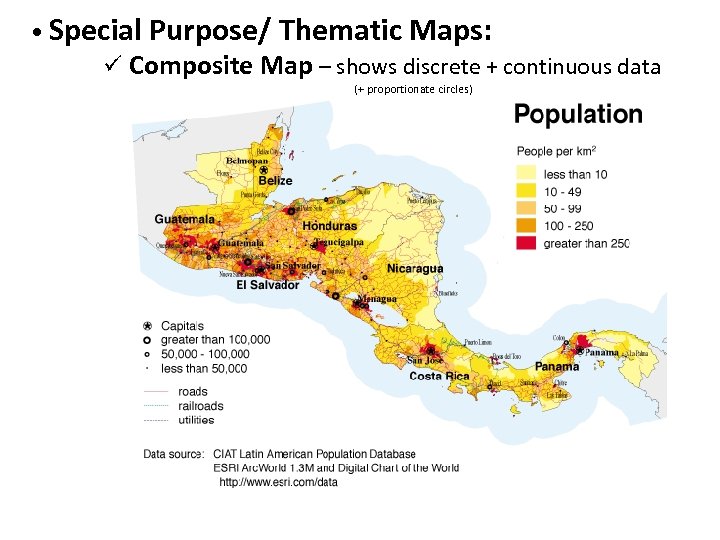• Special Purpose/ Thematic Maps: ü Composite Map – shows discrete + continuous data (+ proportionate circles)