Реология Реология её разделы Наука о течении

Реология

Реология, её разделы Наука о течении и деформации жидких, твердых и газообразных сред, их механическом поведении в процессе течения. Виды реологии: 1. Общая 2. Строительная 3. Техническая 4. Пищевая 5. Биореологическая (течение биологич. сред, живых объектов в жидкости) 6. Мед. реология (изучает реологию крови, урологическая)

Реология, её разделы Деформация – явление смещения условных частиц (микрообъемов) среды под действием внешних сил без нарушения целостности среды. Деформации подразделяют на: упругие – форма восстанавливается после прекращения действия силы; пластические – форма не восстанавливается после снятия действия силы; остаточные – форма восстанавливается частично. Течение – вид деформации, которая продолжается непрерывно с определенной скоростью под действием внешней силы.

Реология, её разделы Пластичность – способность деформироваться как при быстром, так и при медленном действии силы. Ползучесть – способность деформироваться при медленном действии силы. Вязкость – способность среды оказывать сопротивление при перемещении условных частиц среды относительно друга. Напряжение сдвига – отношение силы сопротивления, возникающей при сдвиге слоев, к площади слоев. м²] = [Па Градиент скорости – отношение разности скоростей соприкасающихся слоёв к расстоянию между ними. (м/c) м] = [с-1

Свойства жидкостей Жидкость – одно из агрегатных состояний вещества. Свойства: 1) Молекулы находятся на близких расстояниях – силами взаимодействия между ними нельзя пренебречь. 2) Не сохраняет форму, но сохраняет объем в условиях действия гравитации.

Классификация: 1. По постоянству физических характеристик в разных направлениях: • изотропные (характеристики одинаковы во всех направлениях) – лимфа • анизотропные (характеристики различны во всех направлениях) – жидкое масло. 2. По отношению к законам течения Ньютона: • ньютоновские – подчиняются законам Ньютона (вода, мутные растворы, низкомолекулярные органические жидкости) • неньютоновские – не подчиняются законам Ньютона (цельная кровь, как суспензия форменных элементов в плазме). 3. По электропроводности: • проводящие (кровь) • непроводящие (жидкое масло) 4. По наличию поверхности фазового раздела: • истинные, где отсутствует поверхность раздела между составными частями жидкости. Они прозрачны, молекулы двух разных веществ полностью перемешиваются между собой • квазижидкости, где есть поверхность раздела между составными частями (пена, эмульсии, суспензии).

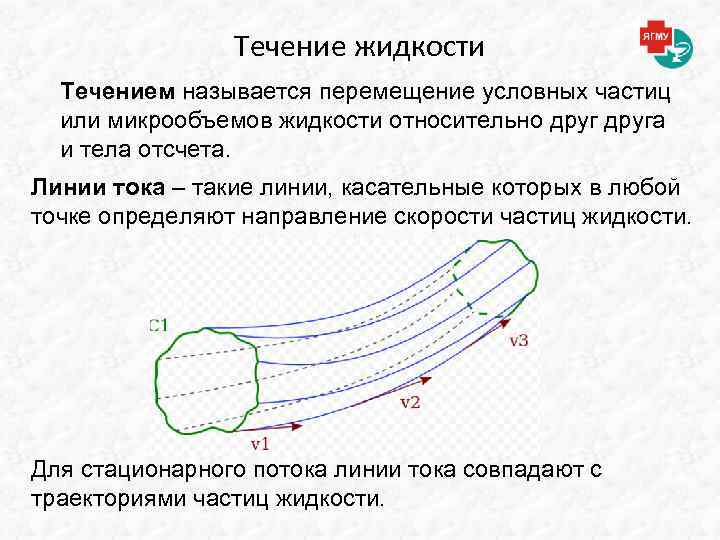Течение жидкости Течением называется перемещение условных частиц или микрообъемов жидкости относительно друга и тела отсчета. Линии тока – такие линии, касательные которых в любой точке определяют направление скорости частиц жидкости. Для стационарного потока линии тока совпадают с траекториями частиц жидкости.

Течение жидкости Трубка тока – часть пространства, ограниченная линиями тока. Текущая жидкость называется потоком. КОЛИЧЕСТВЕННЫЕ ХАРАКТЕРИСТИКИ ПОТОКА Сечение S – площадка, перпендикулярная к направлению течения жидкости, [м²]. Объемный расход Q = V/t – отношение объема, протекающего через площадь сечения, ко времени её протекания, м³ с. Массовый расход M = m/t – отношение массы жидкости, протекающей через сечение, ко времени eё протекания, [кг/с].

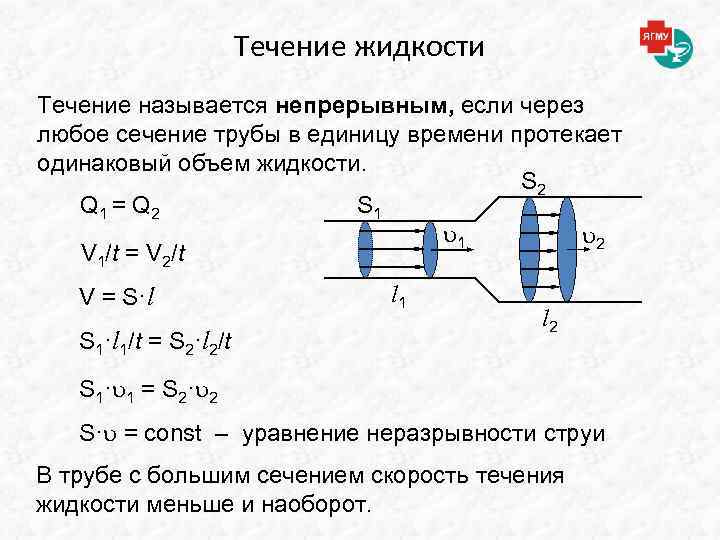Течение жидкости Течение называется непрерывным, если через любое сечение трубы в единицу времени протекает одинаковый объем жидкости. S 2 Q 1 = Q 2 S 1 1 2 V 1/t = V 2/t V = S·l S 1·l 1/t = S 2·l 2/t l 1 l 2 S 1· 1 = S 2· 2 S· = const – уравнение неразрывности струи В трубе с большим сечением скорость течения жидкости меньше и наоборот.

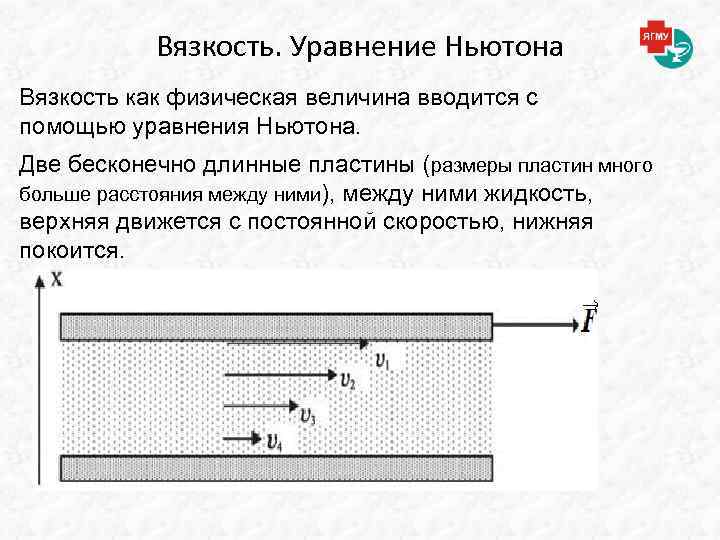Вязкость. Уравнение Ньютона Вязкость как физическая величина вводится с помощью уравнения Ньютона. Две бесконечно длинные пластины (размеры пластин много больше расстояния между ними), между ними жидкость, верхняя движется с постоянной скоростью, нижняя покоится.

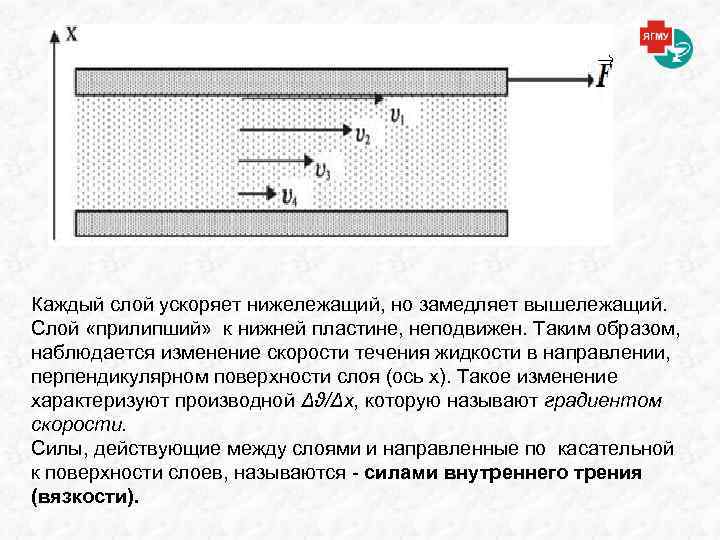Каждый слой ускоряет нижележащий, но замедляет вышележащий. Слой «прилипший» к нижней пластине, неподвижен. Таким образом, наблюдается изменение скорости течения жидкости в направлении, перпендикулярном поверхности слоя (ось х). Такое изменение характеризуют производной Δϑ/Δx, которую называют градиентом скорости. Силы, действующие между слоями и направленные по касательной к поверхности слоев, называются - силами внутреннего трения (вязкости).

Силы вязкости пропорциональны площади взаимодействующих слоев S и градиенту скорости. Для многих жидкостей силы внутреннего трения подчиняются уравнению Ньютона: - физическая форма уравнения Ньютона. S – площадь соприкасающихся слоёв [м 2 ] Δ х – расстояние между осями слоёв [м]. “ ” коэффициент абсолютной (динамической) вязкости [Н·с/м²= Па·с] Этот коэффициент зависит от состояния жидкости и от силы межмолекулярного взаимодействия. При t 0 = 200 С воды =10 ³ [Па·с] При t 0 = 360 С крови=4· 10 ³ [Па·с] Вязкость крови увеличивается при сахарном диабете и уменьшается при туберкулезе. Со значением вязкости связана скорость оседания эритроцитов

Если перенести “S”, то: физическая форма уравнения Ньютона напряжение сдвига градиент скорости Т. о. : реологическая форма уравнения Ньютона

Абсолютная (динамическая) вязкость - равна силе, действующей на слой жидкости единичной площади, . когда градиент скоростей равен единице. Кинематическая вязкость Относительная вязкость [м 2/с] [безразмерная величина]

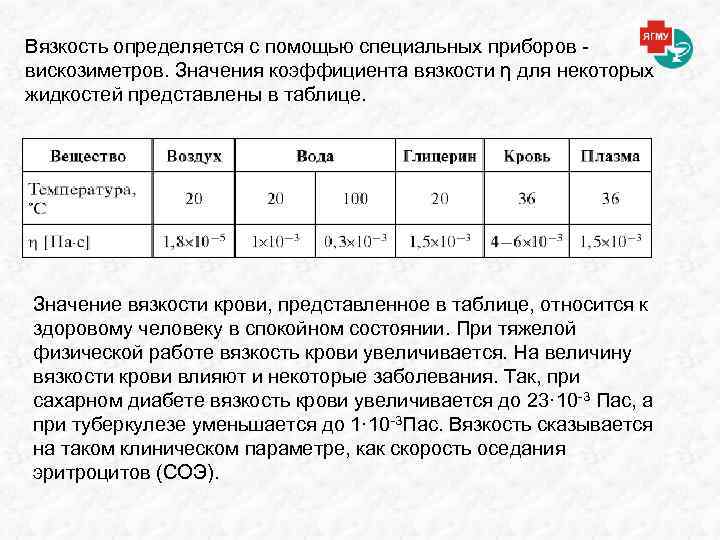Вязкость определяется с помощью специальных приборов - вискозиметров. Значения коэффициента вязкости η для некоторых жидкостей представлены в таблице. Значение вязкости крови, представленное в таблице, относится к здоровому человеку в спокойном состоянии. При тяжелой физической работе вязкость крови увеличивается. На величину вязкости крови влияют и некоторые заболевания. Так, при сахарном диабете вязкость крови увеличивается до 23· 10 -3 Пас, а при туберкулезе уменьшается до 1· 10 -3 Пас. Вязкость сказывается на таком клиническом параметре, как скорость оседания эритроцитов (СОЭ).

Закон Гагена-Пуазейля Гаген (1839 г. ), Пуазейль (1841 г. ) независимо друг от друга установили, что для ламинарно текущей жидкости (p 1 – p 2) = -Δp – разность давлений на концах трубы, r – радиус трубы, l – длина трубы, η – вязкость жидкости. Гаген исследовал движение воды в трубах, Пуазейль – течение жидкостей в капиллярах.

Закон Гагена-Пуазейля Следствия: 1. Объёмный расход пропорционален четвёртой степени радиуса трубки Q ~ r 4. Если при атеросклерозе радиус сосуда уменьшится в два раза, то для поддержания прежнего кровотока перепад давлений нужно увеличить в 16 раз. Сердце будет работать с перегрузкой. Регулировка кровоснабжения органов и терморегуляция осуществляются путём изменения радиуса сосудов. 2. Линейная скорость течения жидкости пропорциональна квадрату радиуса трубки ~ r ².

Закон Гагена-Пуазейля Следствия: 3. Время прохождения равных объемов жидкостей пропорционально их вязкости. 4. Расстояния, пройденные жидкостями за равные промежутки времени, обратно пропорциональны их вязкости.

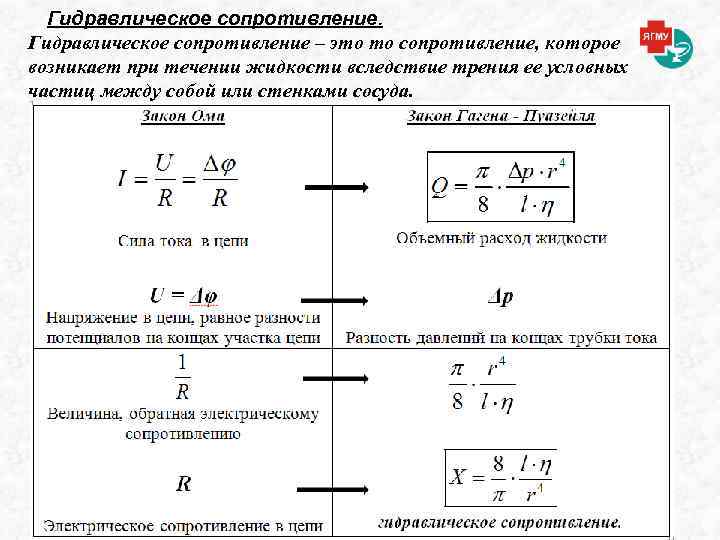Гидравлическое сопротивление – это то сопротивление, которое возникает при течении жидкости вследствие трения ее условных частиц между собой или стенками сосуда.

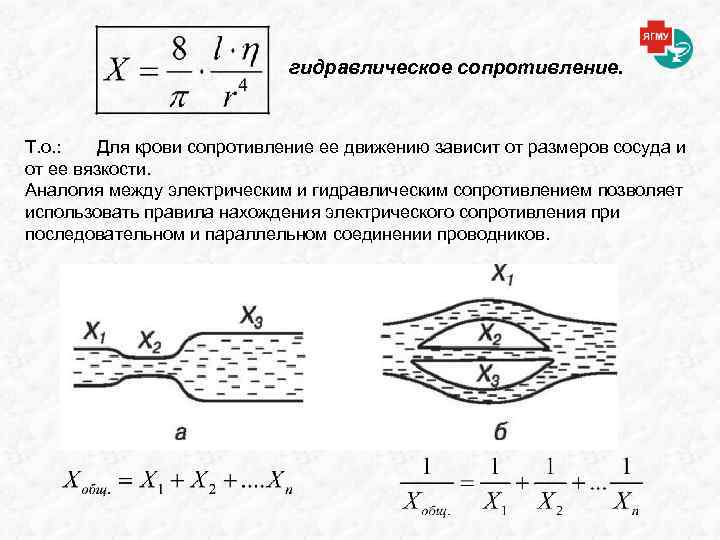гидравлическое сопротивление. Т. о. : Для крови сопротивление ее движению зависит от размеров сосуда и от ее вязкости. Аналогия между электрическим и гидравлическим сопротивлением позволяет использовать правила нахождения электрического сопротивления при последовательном и параллельном соединении проводников.

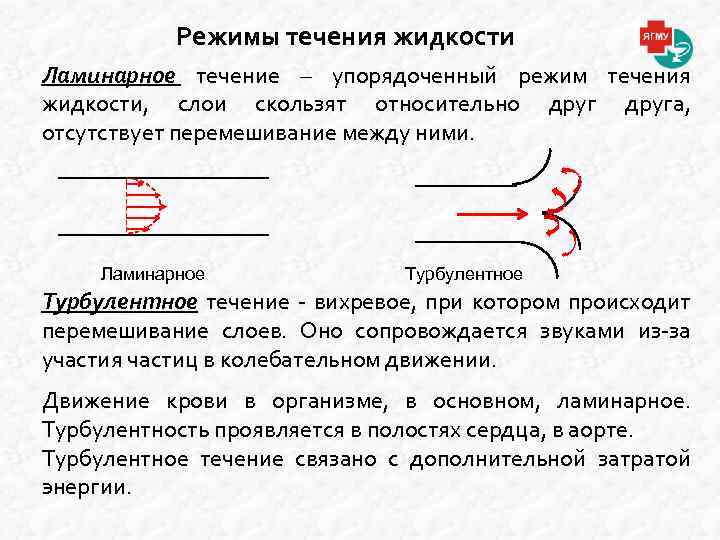Режимы течения жидкости Ламинарное течение – упорядоченный режим течения жидкости, слои скользят относительно друга, отсутствует перемешивание между ними. Ламинарное Турбулентное течение - вихревое, при котором происходит перемешивание слоев. Оно сопровождается звуками из-за участия частиц в колебательном движении. Движение крови в организме, в основном, ламинарное. Турбулентность проявляется в полостях сердца, в аорте. Турбулентное течение связано с дополнительной затратой энергии.

Число Рейнольдса Течение жидкости по трубе зависит от свойств жидкости, скорости её течения и размеров трубы. Осборн Рейнольдс (1842 -1912) изучал переход от ламинарного течения к турбулентному. Турбулентность возникает, когда определенная комбинация величин, характеризующих движение, превосходит некоторое критическое значение. - плотность жидкости - скорость её течения d - диаметр трубы - коэффициент абсолютной (динамической) вязкости

Если число Рейнольдса больше некоторого критического значения Re кр. , то течение турбулентное. Если число Рейнольдса меньше некоторого критического значения Re кр, то течение ламинарное. для крови: Re кр. ≈ 1000, для воды , текущей по круглым гладким трубам: Re кр. ≈ 2300 Критическое значение определяется опытным путем. При моделировании кровеносной системы необходимо, чтобы модель имела такое же Rе, что и объект, иначе между ними не будет соответствия Практическое значение Rе: оно определяет сопротивление, которое оказывает жидкая среда перемещающимся в ней частицами.

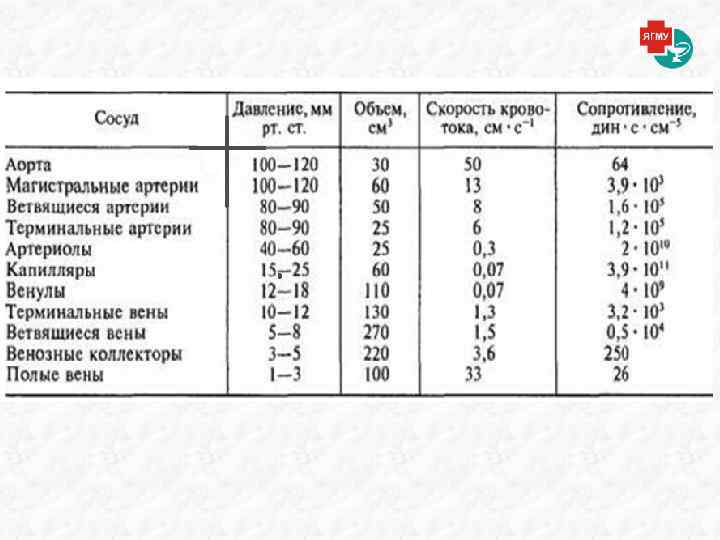
Кровь – жидкая тканевая среда, выполняющая различные функции. Она представляет собой суспензию, состоящую из дисперсной среды (плазмы), и дисперсной фазы ( форменных элементов). Процентный объем форменных элементов в норме 40 - 50% - гематокрит (у мужчин - чуть выше, у женщин – чуть ниже). Объем крови: у мужчин ≈ 5, 2 л у женщин ≈ 3, 9 л Плотность крови ( по отношению к плотности воды) = 1, 05 – 1, 06 г/см 3 Относительная вязкость крови Z=3, 5 5, 5 единиц (по отношению к воде). Реологическая кровь – это неньютоновская жидкость псевдопластического типа. Вязкость тем больше, чем медленнее течёт кровь. Это связано с агрегацией эритроцитов. В неподвижной крови эритроциты агрегируют (образуют “монетные столбики”), при быстром течении крови агрегаты эритроцитов распадаются. Предел текучести 2 -5 м. Па. С увеличением гематокрита предел текучести линейно возрастает. Для крови Rе кр. = 970 ± 80. Течение крови подчиняется закону Гагена –Пуазейля только при условии существования малой разности давлений Δ р на концах сосуда.

В медицине широко используется метод измерения давления крови, предложенный Николаем Сергеевичем Коротковым в 1905 году. Этот метод является основным методом мониторинга артериального давления в клинической медицине, широко используемым во всех странах. На основе этого метода поводятся скрининговые исследования артериального давления различных контингентов здоровых и больных людей. Более того, он является эталоном, по которому тестируются другие приборы. Скрининг - метод активного выявления лиц с какой-либо патологией или факторами риска ее развития, основанный на применении специальных диагностических исследований.

Измерение давления крови Давление крови в артериях больше атмосферного. Тонометр измеряет давление, добавочное к атмосферному. В течение сердечного цикла давление крови изменяется от 16 к. Па (120 мм. рт. ст. ) до 10 к. Па (80 мм. рт. ст. ). pат= 101325 Па = 760 мм. рт. ст. Суть: снаружи прикладывается манжета, в которую нагнетается воздух (увеличивается давление), оно действует на артерию, изменяя режим течения крови, появляются звуки, которые регистрируются.

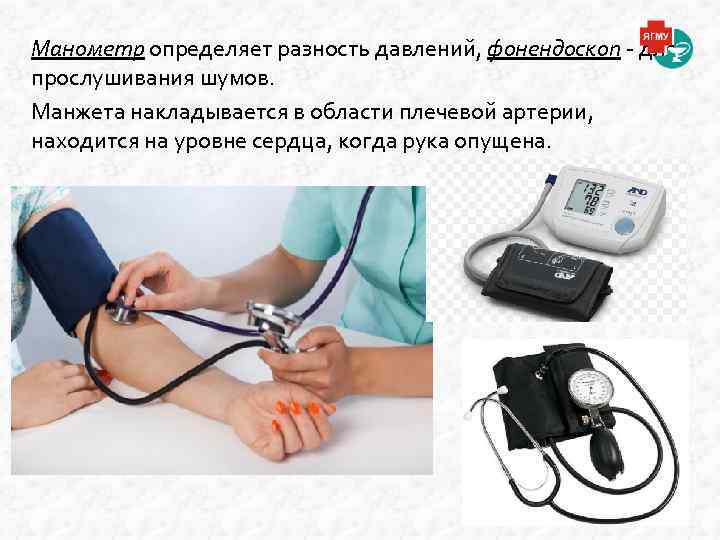Манометр определяет разность давлений, фонендоскоп - для прослушивания шумов. Манжета накладывается в области плечевой артерии, находится на уровне сердца, когда рука опущена.

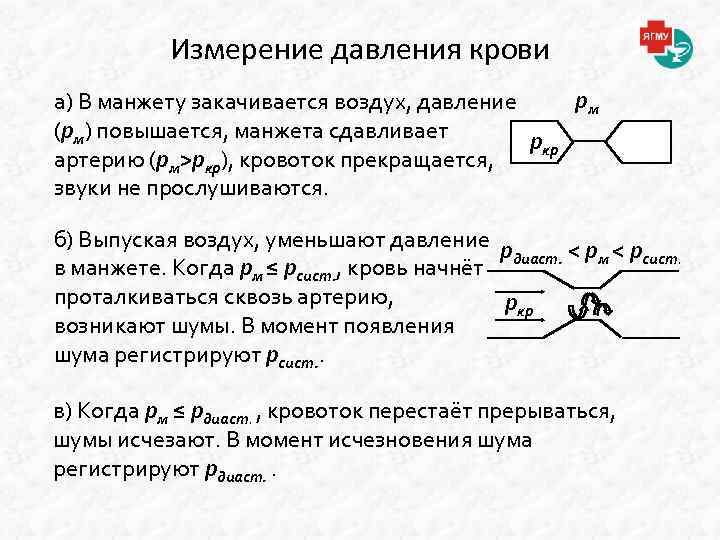Измерение давления крови pм а) В манжету закачивается воздух, давление (pм) повышается, манжета сдавливает pкр артерию (pм>pкр), кровоток прекращается, звуки не прослушиваются. б) Выпуская воздух, уменьшают давление p диаст. < pм < pсист. в манжете. Когда pм ≤ pсист. , кровь начнёт проталкиваться сквозь артерию, pкр возникают шумы. В момент появления шума регистрируют pсист. . в) Когда pм ≤ pдиаст. , кровоток перестаёт прерываться, шумы исчезают. В момент исчезновения шума регистрируют pдиаст. .

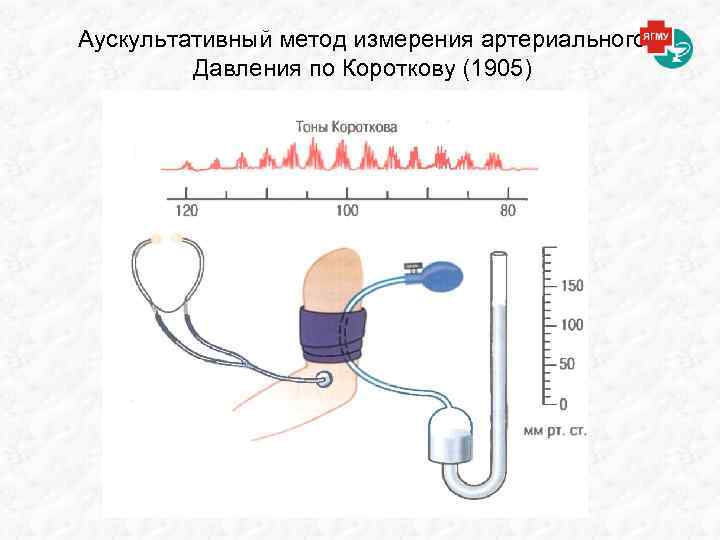Аускультативный метод измерения артериального Давления по Короткову (1905)

Сердечно-сосудистая система Активная часть – сердце, функция – создание разности давлений. Пассивная часть – сосуды: а) аорта – толстая нерастяжимая эластичная трубка d 2 см. б) артерии – более тонкие сосуды, стенки которых состоят из мышечной ткани. в) артериолы – еще более тонкие сосуды, в которых стенки из мышечной ткани. Их основная особенность – изменение просветов сосудов. г) капилляры – состоят из одного слоя клеток. Rе в аорте=5000 (турбулентное) Rе в артерии =100 1000 (ламинарное)

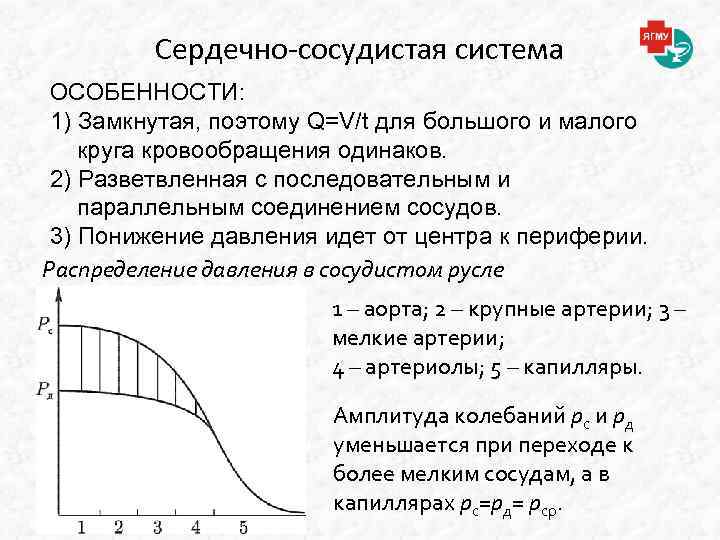Сердечно-сосудистая система ОСОБЕННОСТИ: 1) Замкнутая, поэтому Q=V/t для большого и малого круга кровообращения одинаков. 2) Разветвленная с последовательным и параллельным соединением сосудов. 3) Понижение давления идет от центра к периферии. Распределение давления в сосудистом русле 1 – аорта; 2 – крупные артерии; 3 – мелкие артерии; 4 – артериолы; 5 – капилляры. Амплитуда колебаний pс и pд уменьшается при переходе к более мелким сосудам, а в капиллярах pс=pд= рср.

Из уравнения неразрывности струи [S 1/S 2= 2/ 1] следует, что чем меньше калибр сосуда, тем больше должна быть линейная скорость. Но в реальных условиях скорость потока наивысшая в аорте и по мере перехода от артерии к капиллярам скорость постепенно снижается. Это значит, что существуют иные факторы, определяющие скорость потока, в частности, ветвления сосудов. сечение аорты кровь капилляры На первый взгляд, скорость крови в капиллярах должна увеличиваться , т. к. в них сечение меньше. Но на каждом снижающемся уровне подключено большое число параллельно – соединенных сосудов Суммарное сечение капилляров больше сечения аорты скорость тока крови в сосудистой системе в целом уменьшается и противоречий с уравнением неразрывности струи нет.

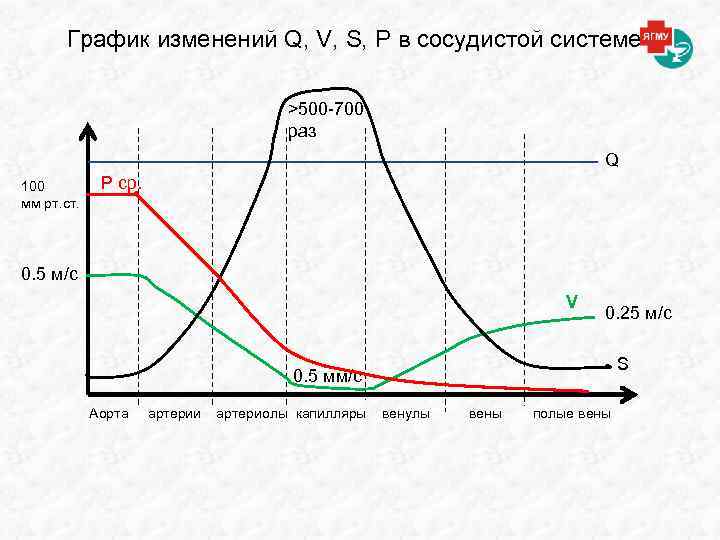График изменений Q, V, S, P в сосудистой системе >500 -700 раз Q 100 мм рт. ст. P ср. 0. 5 м/с V 0. 25 м/с 0. 5 мм/с Аорта артерии артериолы капилляры венулы вены полые вены S

Сердечно-сосудистая система Сердце (ν = 75 уд. /мин, Т = 0. 8 с РАБОЧАЯ ФАЗА (систола) сокращение мышц tс=0. 3 с; pc=16 к. Па ХОЛОСТАЯ ФАЗА (диастола) расслабление мышц tд=0. 5 с; pд=10 к. Па Пульсовая волна – возмущение, образуется в момент выброса крови из левого желудочка; область повышенного давления, распространяющаяся по аорте и артериям. Её можно сравнить с волной на поверхности воды или электрическим импульсом в проводнике – распространяется само возмущение, частицы среды при этом смещаются на гораздо меньшие расстояния. Скорость распространения пульсовой волны 5 -10 м/с. За время систолы S = υ t > 1. 5 м. , пульсовая волна достигает конечностей раньше наступления диастолы.

Сердечно-сосудистая система чем меньше калибр сосуда, тем больше должна быть линейная скорость аорта капилляры скорость 0. 3 – 0. 5 м/с 0. 1 – 0. 5 мм/с диаметр ≈ 2 см 5 – 10 мкм

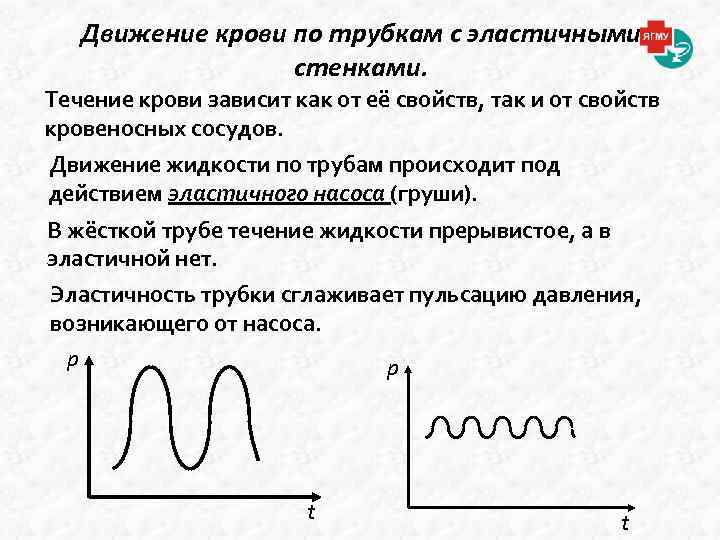Движение крови по трубкам с эластичными стенками. Течение крови зависит как от её свойств, так и от свойств кровеносных сосудов. Движение жидкости по трубам происходит под действием эластичного насоса (груши). В жёсткой трубе течение жидкости прерывистое, а в эластичной нет. Эластичность трубки сглаживает пульсацию давления, возникающего от насоса. p p t t

Трубки с эластичными стенками Выброс крови → повышение давления → растяжение эластичных стенок. Кинетическая энергия жидкости частично переходит в потенциальную энергию деформации. Прекращение работы насоса → понижение давления → эластичная трубка сжимается → жидкость продвигается по трубке. Возникшая деформация распространяется в виде пульсовой волны. Пульсовая волна – возмущение, которое образуется в момент выброса крови из левого желудочка; область повышенного давления, распространяющаяся по аорте и артериям. Потенциальная энергия стенок трубки преобразуется в кинетическую энергию жидкости. Нет больших перепадов скоростей и давлений.

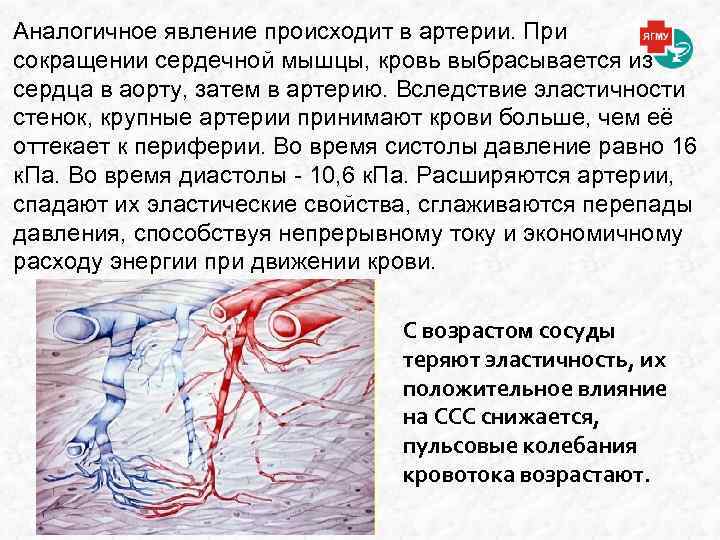Аналогичное явление происходит в артерии. При сокращении сердечной мышцы, кровь выбрасывается из сердца в аорту, затем в артерию. Вследствие эластичности стенок, крупные артерии принимают крови больше, чем её оттекает к периферии. Во время систолы давление равно 16 к. Па. Во время диастолы - 10, 6 к. Па. Расширяются артерии, спадают их эластические свойства, сглаживаются перепады давления, способствуя непрерывному току и экономичному расходу энергии при движении крови. С возрастом сосуды теряют эластичность, их положительное влияние на ССС снижается, пульсовые колебания кровотока возрастают.

Использованная литература 1. Лекции преподавателей ЯГМА (Дигурова И. И. , Крайнова Е. Ю. , Колпаков В. А. ). 2. Сивухин Д. В. Общий курс физики. В 5 т. 2006. 3. Уилкинсон У. Л. Неньютоновские жидкости. 1964. 4. Федорова В. Н. , Степанова Л. А. Краткий курс медицинской и биологической физики с элементами реабилитологии. Лекции и семинары: Учебное пособие. 2005. 5. Химическая энциклопедия. В 5 т. Гл. ред. И. Л. Кнунянц. 1988.