Реология буровых растворов Буровой раствор: …буровой раствор –

Реология буровых растворов Буровой раствор: …буровой раствор – любая жидкость, которая циркулирует в скважине для выноса шлама и выполнения других функций... Уточнение: Буровой раствор чаще всего есть не жидкость, а дисперсная система (ДС).

Реология буровых растворов Терминология Под термином «дисперсная система» понимают еди-нство двух или более фаз. Одна из них является спло-шной и называется дисперсионной средой, а другая – раздроблена (диспергирована) и распределена в пер-вой. Она называется дисперсной фазой (ДФ). Степень раздробленности ДФ называется дисперснос-тью. Системы, состоящие из одной фазы, называются гомогенными. Системы, состоящие из двух и более фаз и имеющие поверхность раздела между фазами, – гетерогенными.

Дисперсная фаза и дисперсионная среда К гомогенным относятся истинные (моле-кулярные) растворы веществ, к гетерогенным – коллоидные растворы, суспензии, эмульсии, пены. Буровые промывочные жидкости – это многокомпонентные двух- или трехфазные гетерогенные системы.

Классификация БПЖ Большинство БПЖ представляет собой дисперс-ные системы, которые могут быть подразделены по следующим признакам:  фазовому состоянию дисперсионной среды;  природе дисперсионной среды;  степени дисперсности дисперсной фазы;  фазовому состоянию дисперсной фазы;  методу получения дисперсной фазы;  природе дисперсной фазы.

Классификация БПЖ Соответствующие данной классификации типы БПЖ принято далее подразделять на различные виды в зависимости от степени минерализации дисперсионной среды, вида растворенных в ней неорганических соединений, характера химической обработки, соотношения между водой и углеводородной жидкостью и т.п.

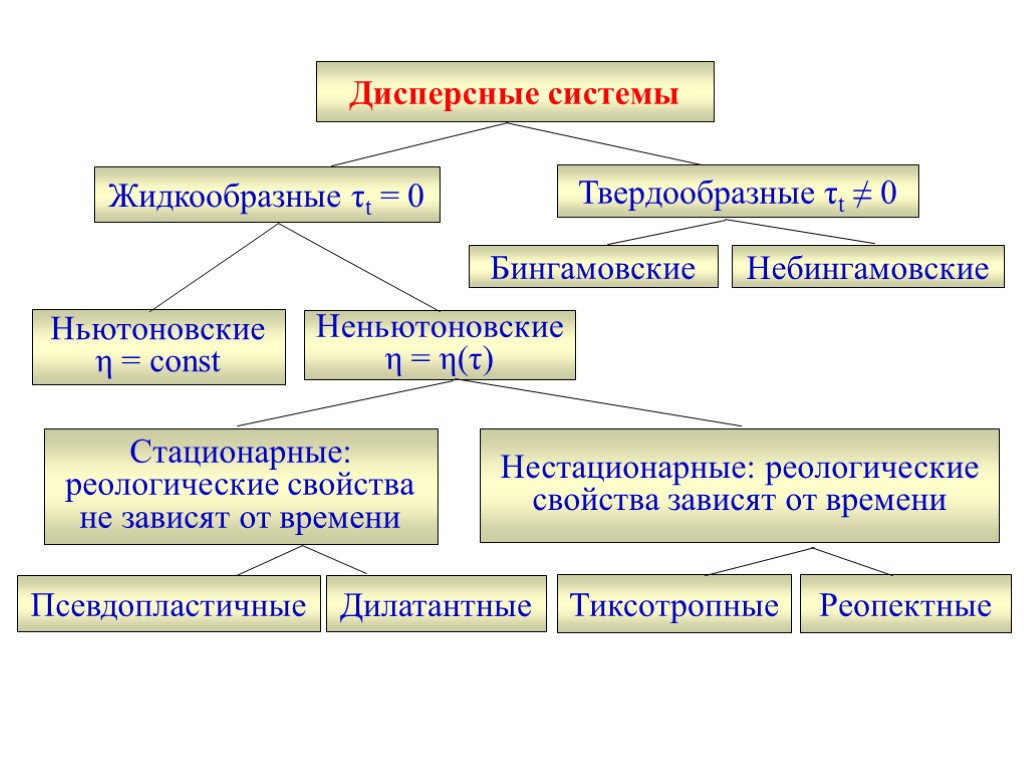
Буровой раствор – дисперсная система Классификация дисперсных систем: по агрегатному состоянию, по кинетическим свойствам, по реологическому поведению.

Классификация ДС по агрегатному состоянию Три агрегатных состояния (твердое, жидкое, газооб-разное) позволяют выделить 9 типов дисперсных систем. Их обозначают дробью, в числителе кото-рой обозначено агрегатное состояние дисперсной фазы, а в знаменателе- состояние дисперсионной среды: т/т, ж/т, г/т т/ж, ж/ж, г/ж т/г, ж/г, г/г

Классификация ДС по агрегатному состоянию Дисперсионная среда у гетерогенных дисперсных систем, используемый в бурении, представлена жидкостью (вода, нефть, дизельное топливо, синтетическая жидкость); дисперсная фаза представлена • твердыми частицами: глинистые минера-лы, утяжелители, наполнители (суспензии, золи); • жидкостью, нерастворимой в дисперсион-ной среде: нефтью, дизельным топливом (эмуль-сии); • газом (пены и аэрированные жидкости).

Классификация ДС по кинетическим свойствам По кинетическим свойствам все дисперсные системы делят на два класса: Свободнодисперсные: дисперсная фаза подвижна, а дисперсионная среда – жидкость (коагуляционные ДС), Связнодисперсные: твердая дисперсионная среда, в которой частицы дисперсной фазы не могут свободно передвигаться (конденсационно-кристаллизационные ДС) .

Классификация ДС по кинетическим свойствам В основе деления дисперсных систем на сво-боднодисперсные и связнодисперсные сис-темы лежит различие в виде взаимодейст-вия частиц дисперсной фазы.

Классификация ДС по кинетическим свойствам В связнодисперсных конденсационно-кристаллизационных системах происходит химическое взаимодействие между части-цами и их срастание с образованием жест-кой объемной структуры. При срастании частиц механические свойства структур соответствуют свойствам самих частиц.

Классификация ДС по кинетическим свойствам В свободнодисперсных дисперсных системах реализуется коагуляционное взаимодействие частиц дисперсной фазы. Коагуляция - слипание частиц ДФ в резуль-тате адгезионного, вандерваальсового взаи-модействия частиц между собой. Механические свойства коагуляционных стру-ктур определяются во многом особенностями межчастичных связей и прослоек среды.

Классификация ДС по кинетическим свойствам Коагуляционные структуры имеют жид-кую дисперсионную среду. Для них харак-терна способность восстанавливать свою структуру во времени после ее механичес-кого разрушения. Это явление называется тиксотропией. Восстановление структурных связей сопро-вождается изменением вязкости ДС во времени.

Дисперсная фаза – глинистые минералы Дисперсная фаза буровых растворов – глинистые минералы. Глинистые минералы, образованные в процессе химического выветривания горных пород силикатной группы, отличаются высокой дисперсностью (линейный размер глинистого минерала -10-6 м и менее, удельная поверхность каолинита достигает 10 м2/г, а монтмориллонита - 800 м2/г) и слоисто-ленточным строением. Но главнейшей особенностью глинистых минералов является их способность к электрическому заряжению своей поверхности в результате изоморфизма.

Дисперсная фаза – глинистые минералы При гетеровалентном изоморфизме с поверхности глинистого минерала уходит четырехвалентный ион кремния Si+4, а на его место из окружающей среды может прийти любой другой ион с меньшей или большей валентностью. В этом случае и возникает нарушение электронейтральности глинистого минерала. Чаще всего на поверхности образуется отрицатель-ный электрический заряд, т.к. на место иона кремния приходят ионы меньшей валентности (Al+3, Ba+2, Ca+2 и др.). Величина заряда определяется интенсив-ностью изоморфных замещений и валентностью замещающего иона.

Дисперсная фаза – глинистые минералы По величине структурного отрицательного заряда глинистые минералы располагаются в следующей последовательности: каолинит < монтмориллонит < гидрослюда

Дисперсная фаза – глинистые минералы В естественных условиях залегания глинистой горной породы отрицательный заряд поверхнос-ти глинистых минералов нейтрализован катиона-ми-компенсаторами, которые располагаются на внешней поверхности глинистой частицы: положительные катионы, с одной стороны, и от-рицательные заряды глинистой частицы, с другой стороны, образуют двойной электрический слой. Двойной электрический слой состоит из адсорбционного и диффузионного слоев ионов.

Дисперсная фаза – глинистые минералы Глинистый минерал вместе с возникшим двойным электри-ческим слоем образует мицеллу, размер которой значитель-но превосходит размер частицы глинистого минерала (ядро мицеллы). В результате мицеллообразования объем глинис-той горной породы при увлажнении увеличивается много-кратно, причем процесс набухания развивается во времени. Размер мицеллы определяется природой глинис-того минерала: чем больше величина структурного отрицательного заряда на поверхности глинистого минерала и выше дисперсность, тем больше прирост объема.

Дисперсная фаза – глинистые минералы В водной среде вокруг ядра возникает раствор с ано-мальными физическими свойствами: в адсорбционной части двойного электрического слоя, т.е. непосредст-венно около ядра мицеллы, образуется прочносвязан-ная вода. В диффузионном слое возникает связанная вода. Образование связанной воды приводит к тому, что глинистая горная порода, будучи высокопористой (пористость доходит до 70 %), тем не менее, является водонепроницаемой. Фильтрация жидкости через поры, в которых находится связанная вода, возможна только при создании значительного перепада давления.

Дисперсная фаза – глинистые минералы Электрические заряды разного знака, находящиеся на поверхности глинистых минералов, обеспечивают взаимодействие частиц друг с другом, играют важ-ную роль в процессах структурообразования в ДС: возникает жесткий каркас, способный удерживать на себе падающие частицы шлама. ДС, у которой ДФ долгое время сохраняет седимен-тационную устойчивость (не выпадает в осадок ДФ), называется структурированной.

Дисперсная фаза – глинистые минералы В БПЖ, как в дисперсных системах, образу-ется пространственная коагуляционная структура, определяющая их основные свойства. Дисперсная фаза в виде мицеллы - глинистой частицы, покрытой гидратной оболочкой Дисперсионная среда – межмицел-лярная жидкость (свободная и связанная вода)

Реология БПЖ Реологические модели описывают связь между напряжением сдвига и деформацией сдвига, скоростью сдвига в буровом растворе.

Реология БПЖ Идеальные реологические тела: Виды деформаций: Упругая Пластическая Вязкая

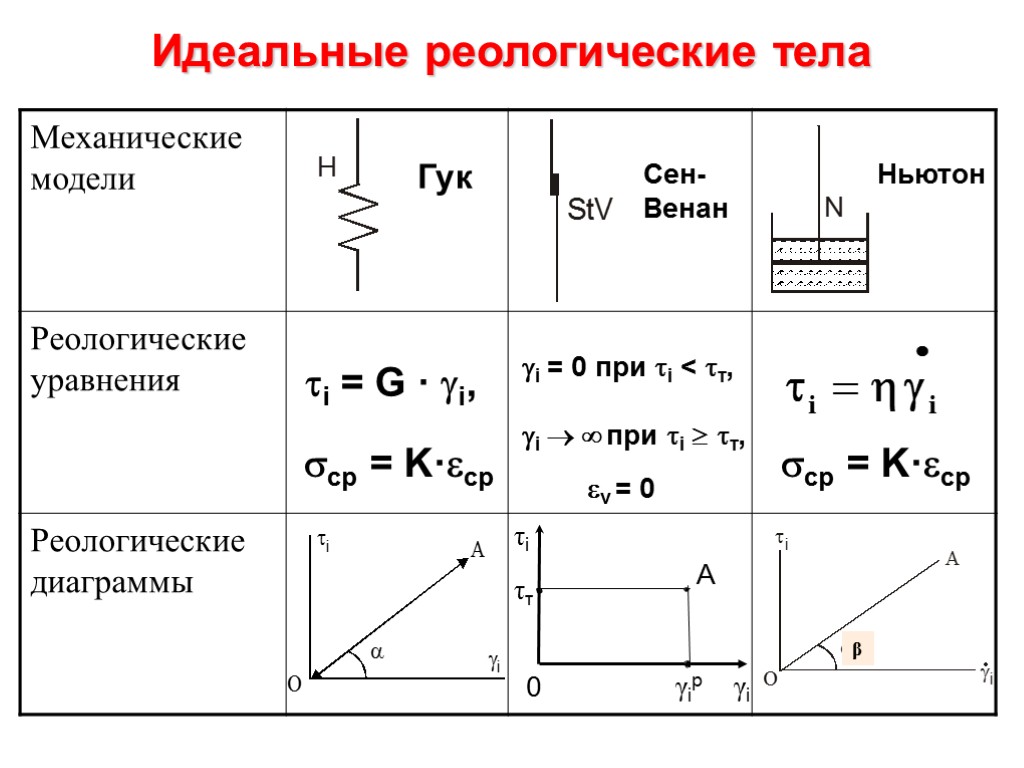
Идеальные реологические тела Гук Сен-Венан Ньютон ti = G · gi, sср = K·eср gi = 0 при ti < tт, gi ® ¥ при ti ³ tт, ev = 0 sср = K·eср β

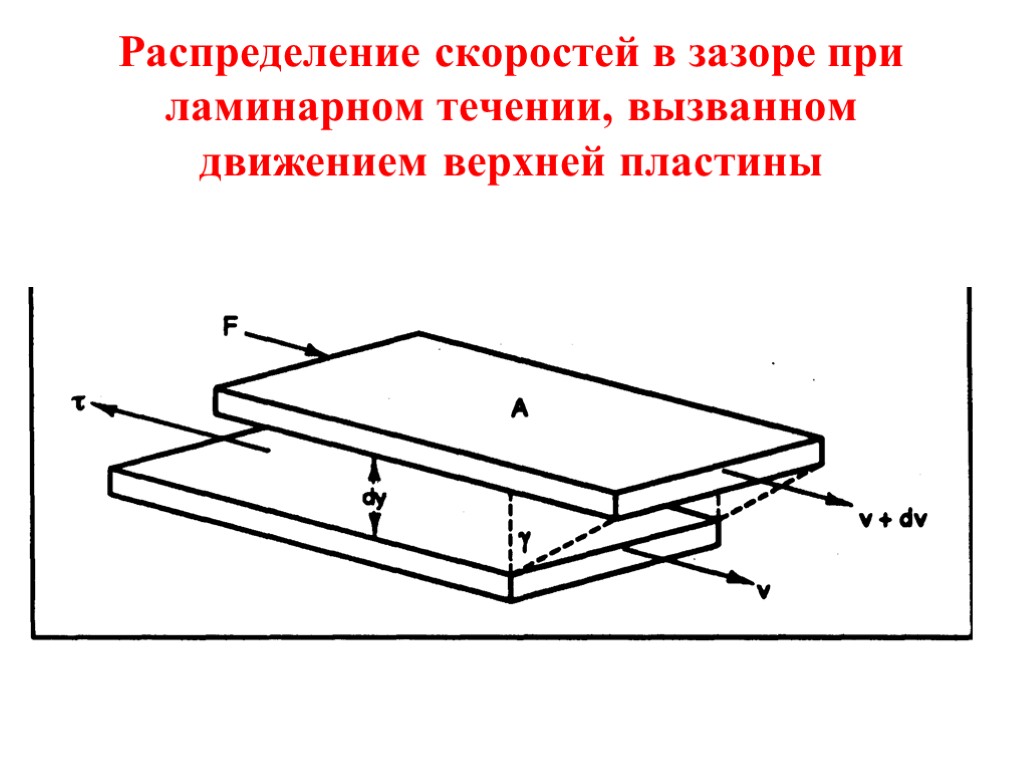
Распределение скоростей в зазоре при ламинарном течении, вызванном движением верхней пластины

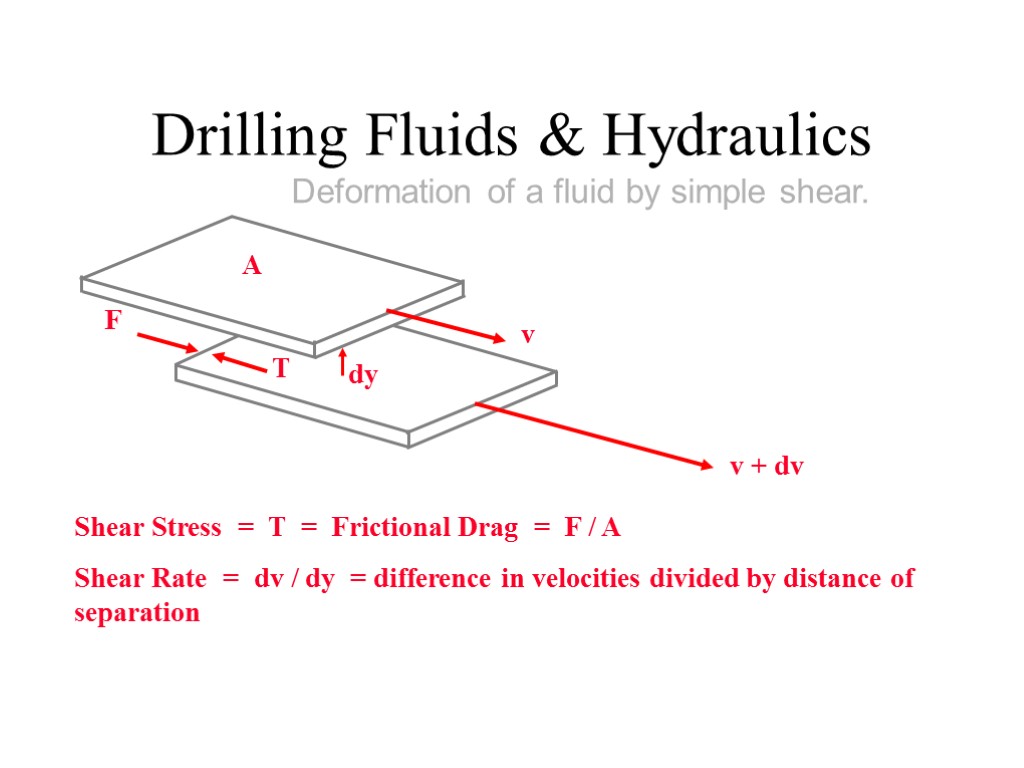
Drilling Fluids & Hydraulics Deformation of a fluid by simple shear. T Shear Stress = T = Frictional Drag = F / A Shear Rate = dv / dy = difference in velocities divided by distance of separation A v + dv v dy

Напряжение сдвига Прилагаемая сила F, воздействуя на площадь А, заставляет слои скользить один относительно другого. Между слоями жидкости возникает касательное напряжение или «напряжение сдви-га» τ : τ = F / A Dim τ = Н/м2. Слои жидкости сдвигаются один относительного другого легче, чем слой раствора относительно стенки трубы. Поэтому очень тонкий слой жидкости непосредственно у стенки трубы можно считать неподвижным.

Скорость сдвига Разница скоростей ΔV между двумя сло-ями раствора, разделенная на величину расстояния между ними Δу, называется скоростью сдвига, градиентом скорости: = ΔV / Δу = dV/dу Dim = (м/с)/м = 1/с = с-1 .

Причина тождества «Градиент скорости ≡ скорость сдвига»

Ламинарное течение ВЖ в кольцевом канале под действием вращения наружного цилиндра Реологическое уравнение состояния для вращательного движения имеет вид η

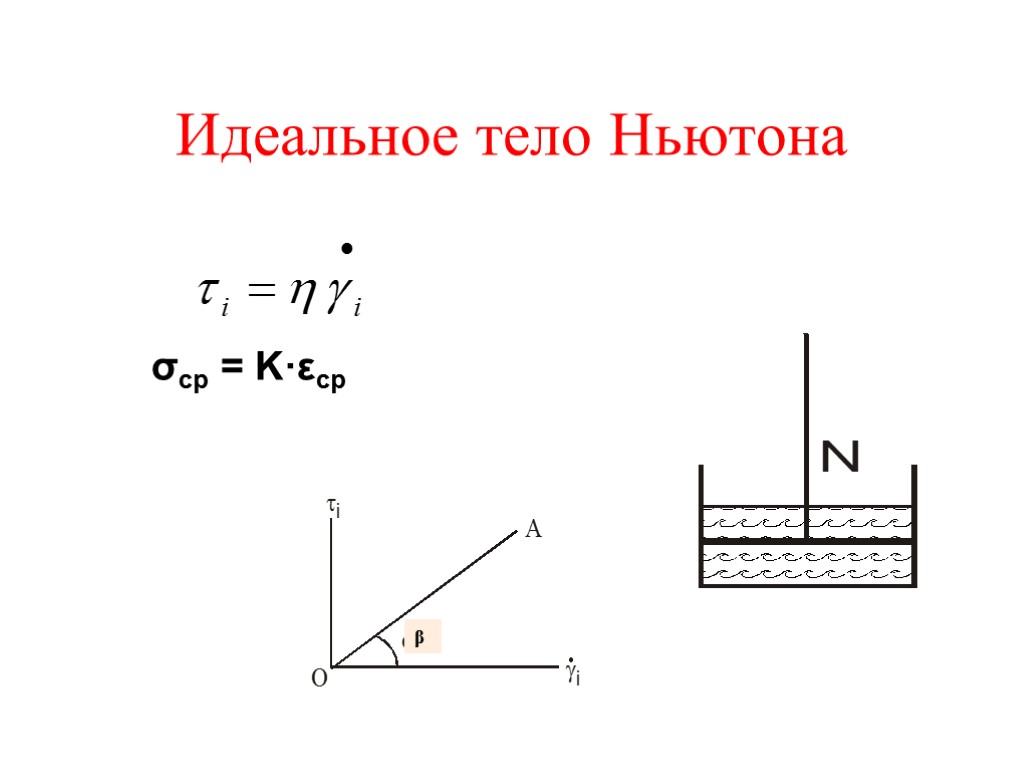
Идеальное тело Ньютона β σср = K·εср

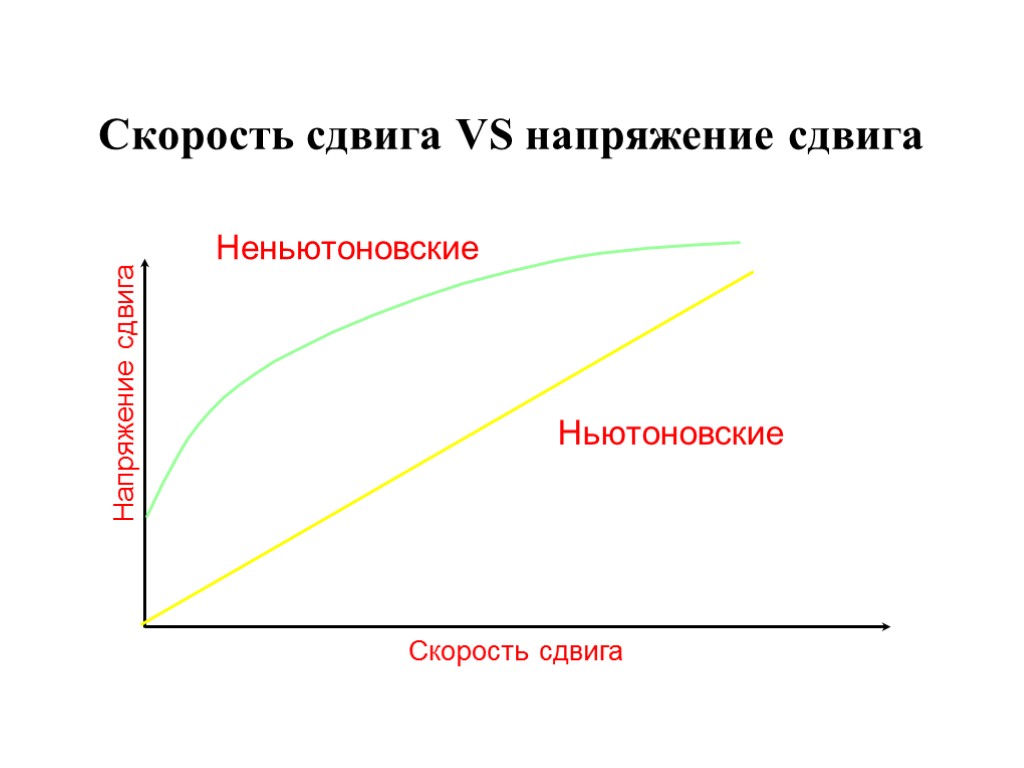
Реологические особенности ньютоновской жидкости Напряжение сдвига прямо пропорционально скорости сдвига. - жидкости: вода, глицерин, легкие нефти, спирт и пр. Характеризуются одним реологическим парамет-ром: коэффициентом динамической вязкости η. Dim η = Па·с. Вязкость ньютоновской жидкости одинакова при любой величине скорости сдвига. Зависит от температуры.

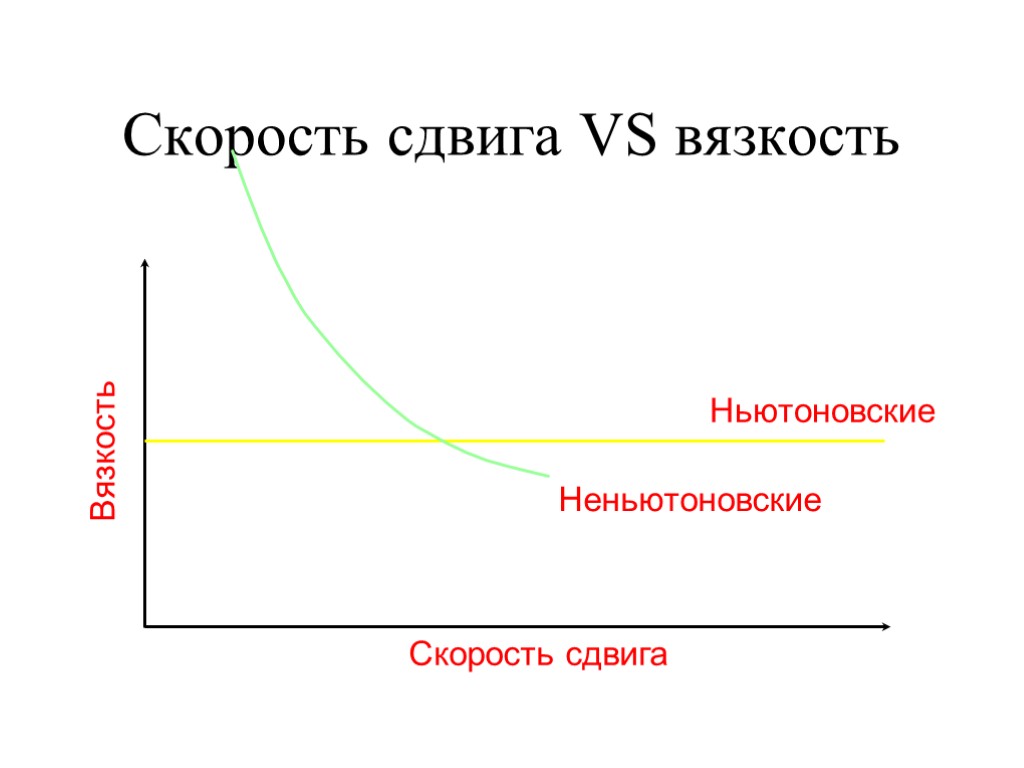
Скорость сдвига VS вязкость Вязкость Скорость сдвига Ньютоновские Неньютоновские

Величина скорости сдвига в элементах циркуляционной системы В циркуляционной системе скважины скорость сдвига меняется в очень широких пределах: в бурильной колонне от 100 до 500 с-1, в УБТ от 700 до 3000 с-1; в затрубном кольцевом пространстве от 10 до 500 с-1, чаще всего 100 с-1; в насадках долот от 10 000 до 100 000 с-1.

Моделирование БПЖ С точки зрения реологии, буровой раствор является сложным телом, его свойства можно передать либо - комбинацией идеальных тел: H, StV, N (последовательное, параллельное соединение элементов), - изменением реологического уравнения состояния Ньютоновской жидкости с помощью понятия «физическая нелинейность»: Аномальные жидкости

ПРАВИЛА ПОСТРОЕНИЯ СЛОЖНЫХ ТЕЛ t = t1 = ... = tn, g = g1 + ... + gn t = t1 + ... + tn , g = g1 = ... = gn 1. Последовательное соединение элементов 2. Параллельное соединение элементов СЛОЖНЫЕ РЕОЛОГИЧЕСКИЕ ТЕЛА 1. Тело Прандтля: P = H – StV γs – γe = γp

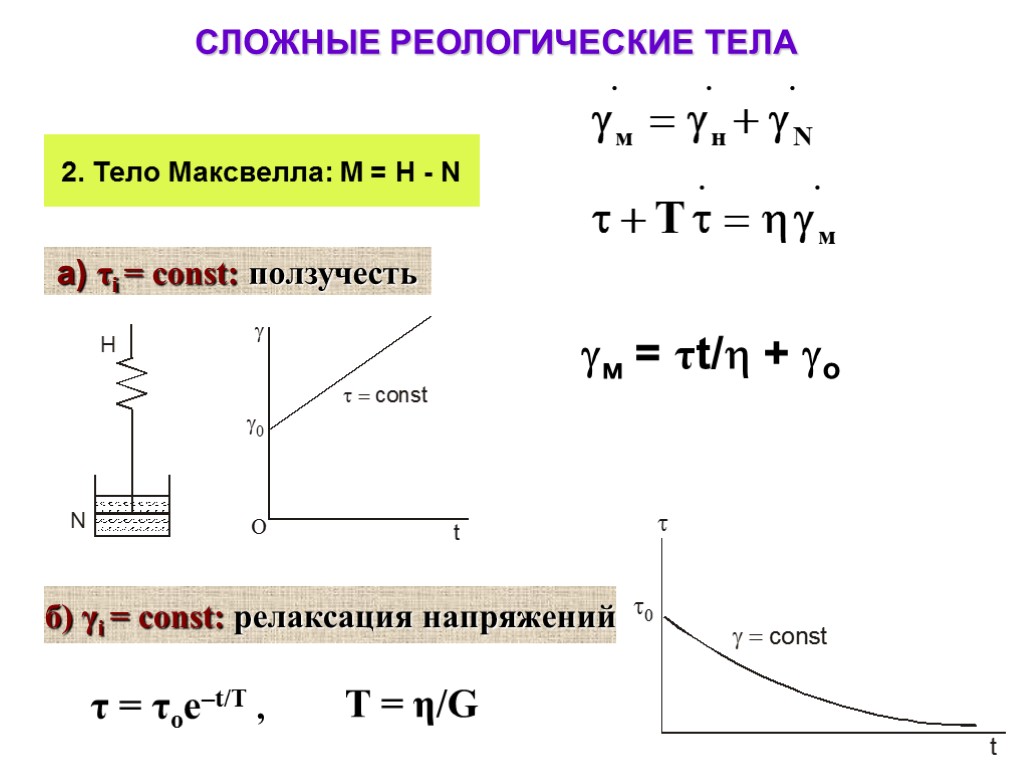
СЛОЖНЫЕ РЕОЛОГИЧЕСКИЕ ТЕЛА 2. Тело Максвелла: М = Н - N а) τi = const: ползучесть gм = τt/h + gо б) γi = const: релаксация напряжений τ = τоe–t/T , T = η/G

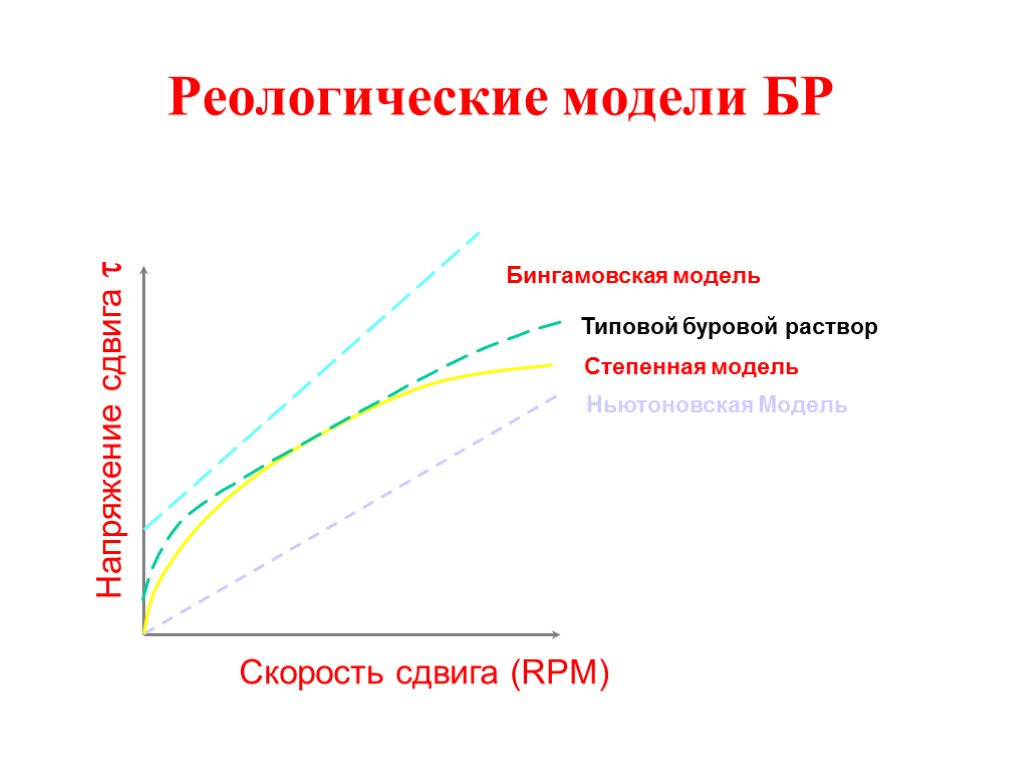
Реологические модели БР Напряжение сдвига  Скорость сдвига (RPM) Ньютоновская Модель Степенная модель Бингамовская модель Типовой буровой раствор

Тело Бингама: В = H — (N│StV) Реологическое уравнение состояния Реологическая диаграмма τT – динамическое напряжение сдвига (СНС) ηП - пластическая вязкость, зависит от температуры и давления; от времени не зависит.

Бингамовская УВПЖ Ее отличает линейная зависимость между скоростью сдвига и напряжением сдвига (линейно-вязкая жидкость). Базируется на реологических замерах при минимум двух (можно и более) фиксированных скоростях сдвига 300 rpm, 600 rpm для построения реологической кривой.

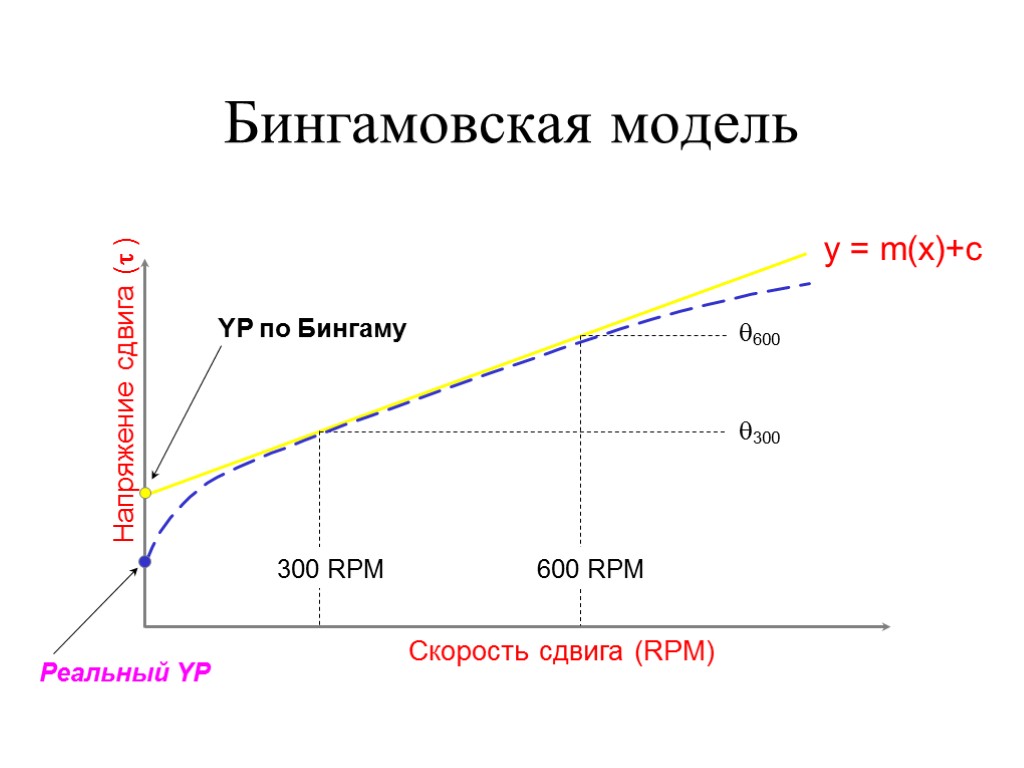
Бингамовская модель Напряжение сдвига ( ) Скорость сдвига (RPM) 300 RPM 600 RPM q600 q300 YP по Бингаму y = m(x)+c Реальный YP

Модель Бингама

Статическое напряжение сдвига (СНС) Yield Point (YP) т характеризует сопротивление, возникающее при течении вследствие действия электрических сил притяжения-отталкивания между частицами ДФ. Движения раствора не происходит до тех пор, пока это напряжение (т) не будет преодолено. Величина напряжения т – это функция: типа частиц ДФ, плотности зарядов на поверхно-сти глинистого минерала, концентрации частиц ДФ, толщины ДЭС, природы ионов и их концентрации. Единица измерения: Lbs/100 ft2, Pascals – Pa, Па

Пластическая вязкость Пластическая вязкость ηп характеризует внутрен-нее трение между соседними слоями дисперсион-ной среды, диспергированными частицами ДФ, а также межфазное взаимодействие. Величина пластической вязкости зависит от вяз-кости дисперсионной среды, от концентрации, размеров и формы частиц ДФ: пластическая вязкость увеличивается с ростом концентрации частиц ДФ и их дисперсности.

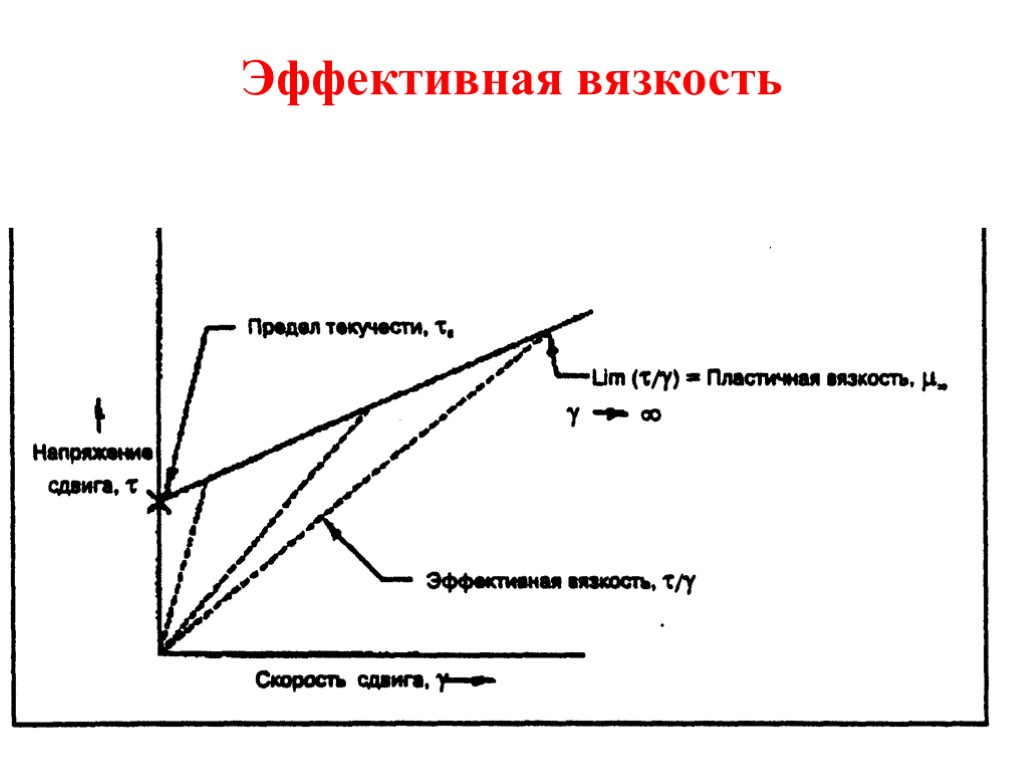
Эффективная вязкость

Эффективная вязкость В вязкопластичной модели Бингама эффективная вязкость, определяе-мая как напряжение сдвига, деленное на скорость сдвига, изменяется в зависимости от изменения скорости сдвига. Эффективная вязкость определяется наклоном линии от точки пересечения координат в направлении напряжении сдвига при каком- то определенном значении скорости сдвига. Наклоны пунктирных линий представляют собой эффективную вязкость при различных значениях скорости сдвига. Эффективная вязкость снижается при повышении скорости сдвига. По мере того, как скорость сдвига приближается к бесконечности, эффективная вязкость достигает предела, называемого «пластической вязкостью - PV». Пластическая вязкость жидкости по Бингаму представляет собой наименьшее значение, которое может иметь эффективная вязкость при бесконечно высокой скорости сдвига или, по другому говоря, при наклоне прямой пластичности по Бингаму.

Пластическая вязкость Возможные пути снижения пластической вяз-кости: разжижение раствора, механическое удаление частиц ДФ и предотвращение их диспергирования в растворе. С увеличением пластической вязкости возра-стают гидравлические сопротивления в цир-куляционной системе скважины, снижается ресурс работы буровых насосов, а также доля гидравлической мощности, подводимой к забойному двигателю и долоту.

Бингамовская модель: проблемы Модель неточно воспроизводит поведение бурово-го раствора при низких скоростях сдвига: - при скоростях сдвига, меньших 300 RPM, неко-торые растворы ведут себя иначе, чем данная модель - YP по Бингаму выше, чем реальное YP раствора.

Тело Бингама В = H — (N│StV) Реологическое уравнение Реологическая диаграмма τT – статическое напряжение сдвига (СНС) ηП - пластическая вязкость

АНОМАЛЬНЫЕ ЖИДКОСТИ Неньютоновские жидкости - диспер-сные системы: псевдопластичные, дилатантные. Течение этих жидкостей начинается при любом ненулевом значении касательного напряжения и кривая течения выходит из начала координат на плоскости τ – dV/dr.

Псевдопластичные В природе чаще встречаются псевдопла-стичные жидкости. Вязкость этих жидкос-тей уменьшается с ростом касательных на-пряжений : эти жидкости при росте  раз-жижаются. Объясняется такое поведение ориентированием в потоке жидкости взве-шенных в ней несимметричных твердых час-тиц суспензий или развертыванием цепей полимеров таким образом, что течению оказывается минимальное сопротивление.

Дилатантные Значительно реже встречаются жидкости, вяз-кость которых увеличивается с ростом касате-льных напряжений . Такое поведение объясняется разрушением агрегатов твердых частиц в потоке. Это приво-дит в росту концентрации твердых частиц в жидкости, и, как следствие, увеличению тре-ния между частицами, что и вызывает рост вязкости.

Неньютоновские буровые жидкости Псевдопластичные жидкости (ППЖ) Течение ППЖ начинается при любом ненулевом значении касательного напряжения. Эти буровые растворы отличает более сложная связь между нап-ряжением сдвига и скоростью сдвига, чем у ньюто-новской жидкости: вязкость зависит от величины скорости сдвига – физическая нелинейность:

Псевдопластичные жидкости (ППЖ) ППЖ разжижаются при увеличении скорости сдвига: при ламинарном режиме течения раствор более жидкий при высокой скорости сдвига, чем при низкой. Реологическое уравнение состояния имеет вид:

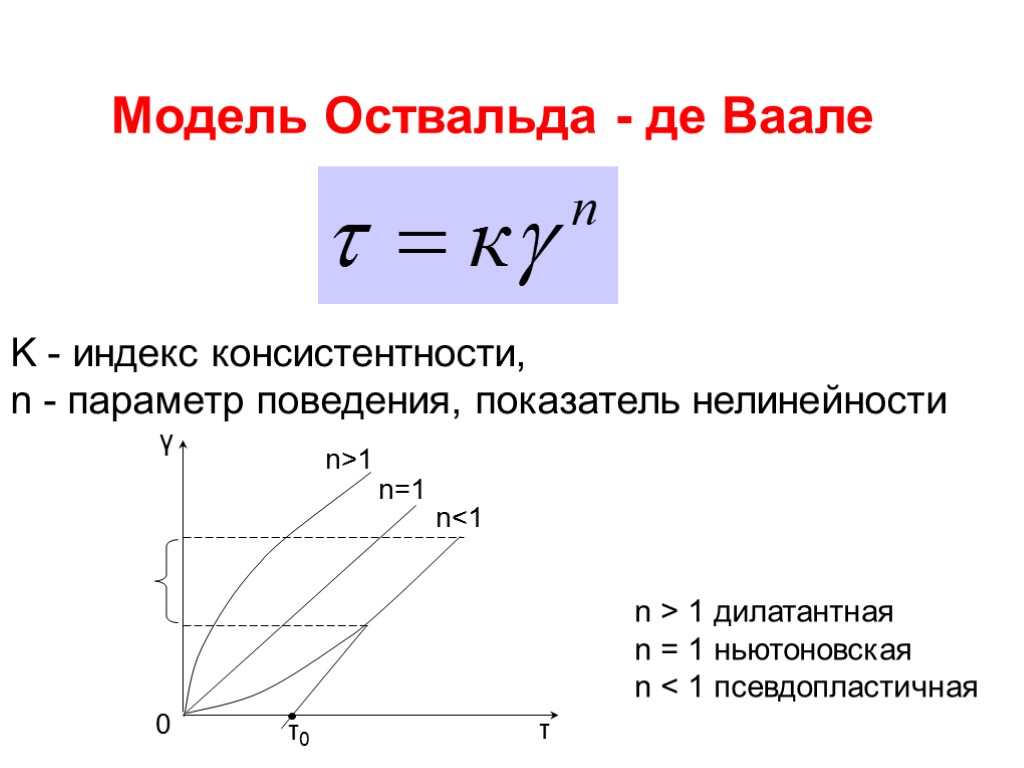
Модель Оствальда - де Ваале K - индекс консистентности, n - параметр поведения, показатель нелинейности n > 1 дилатантная n = 1 ньютоновская n < 1 псевдопластичная

Степенная модель Оствальда-де Ваале Реологическая кривая степенного закона всегда начинается с нуля (YP = 0), т.е. отсутствуют пластические свойства. Реальное значение YP раствора всегда больше нуля. Модель обеспечивает лучше реальную зависимость, чем модель Бингама. Реологическое уравнение состояния: Напряжение сдвига = K·(скорость сдвига)n Где K - коэффициент пропорциональности (консистентность), n - показатель поведения раствора

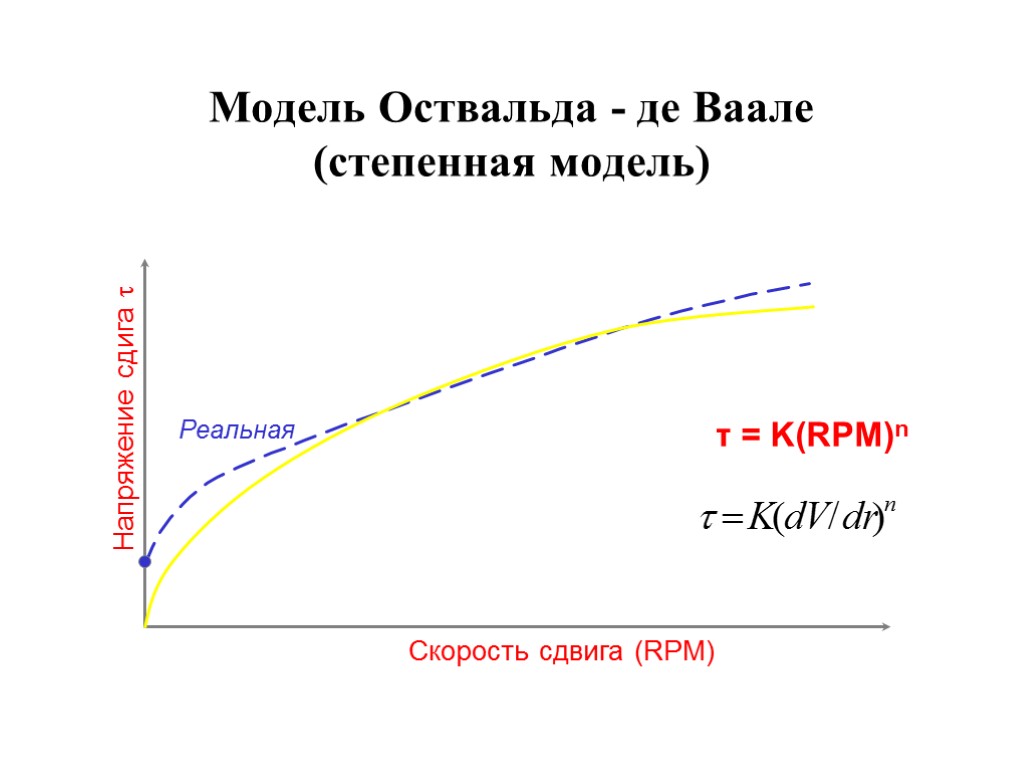
Модель Оствальда - де Ваале (степенная модель) Напряжение сдига  Скорость сдвига (RPM) τ = K(RPM)n Реальная

Remember: У неньютоновских промывочных жидкостей вязкость меняется с изменением скорости сдвига и без указания на скорость сдвига термин «вязкость» применительно к неньюто-новским «жидкостям» теряет смысл.

При помощи модели Оствальда - де Ва-але описывается поведение эмульсий, паст, мыльных составов, клея, красок, буровых и тампонажных растворов.

Физическая суть реологических параметров K, n К – более общее понятие, чем вязкость. C ростом K растет транспортирующая способность буро-вого раствора, но одновременно увеличивают-ся и гидравлические сопротивления в циркуля-ционной системе скважины. Растет амплитуда колебания давления при страгивании бурового раствора после останов-ки работы насоса (это повышает вероятность возникновения гидроразрыва пластов).

Физическая суть реологических параметров K, n Величина n влияет на форму профиля скорости при течении промывочной жидкости: более плоский профиль возникает при малых значе-ниях n . Это приводит к повышению транспортирую-щей способности промывочной жидкости, т.к. основная масса шлама оказывается в зоне максимальных скоростей.

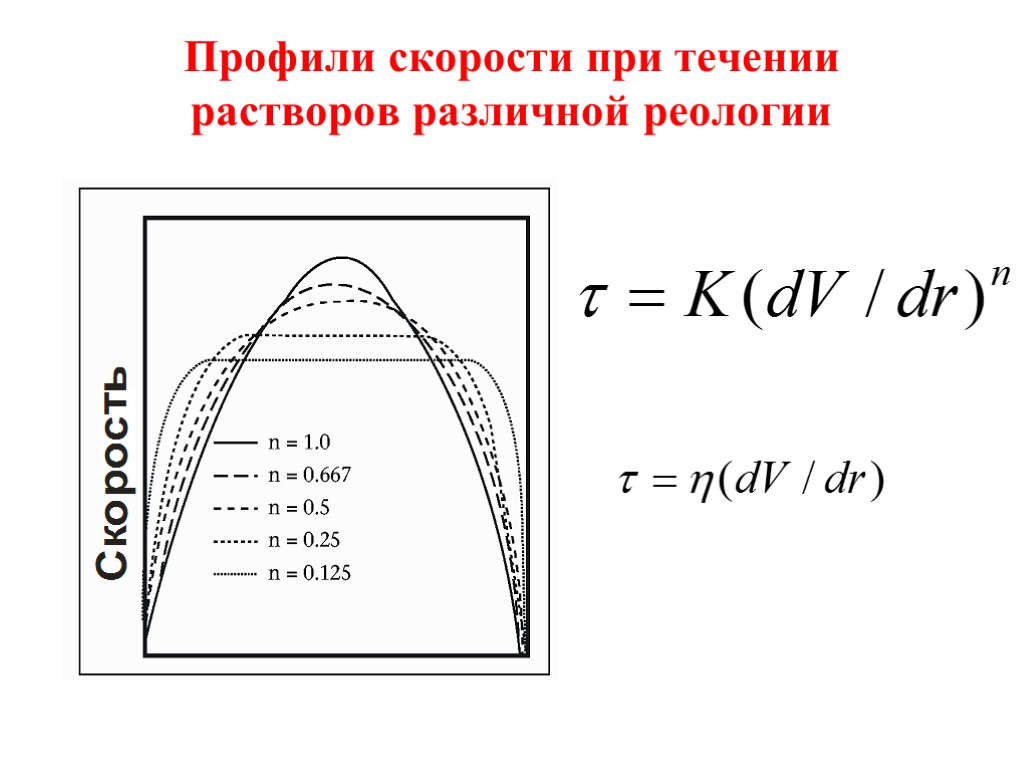
Профили скорости при течении растворов различной реологии

Степенная модель: проблемы При малых скоростях сдвига модель не точно описывает поведение бурового раствора: значение YP бурового раствора всегда больше нуля.

Модифицированная степенная модель Модель Herschel-Bulckley (Модифицированная Степенная Модель) Лучше описывает течение раствора Включает ненулевое значение YP  = t + K(dV/dr)n Рекомендовано Американским Нефтяным Институтом (API) “Recommended Practice On The Rheology And Hydraulics Of Oil-Well Drilling Fluids,” June 1995 API Recommended Practice 13D Third Edition

Скорость сдвига VS напряжение сдвига Напряжение сдвига Скорость сдвига Ньютоновские Неньютоновские

Модифицированная степенная модель Модель Гершеля - Балкли используется для описания поведения буровых растворов с низким содержанием твердой фазы, обрабо-танных полимерными реагентами. Они отли-чаются малым значением t , а при развитии деформаций ведут себя как структурирован-ные жидкости. Практическое использование модели Гершеля-Балкли сдерживается тем, что определение реологических параметров для этих моделей и интегрирование уравнений их движения (течения) весьма затруднительно.

Практическое применение В настоящее время для практических целей используются более простые мо-дели Бингама, Оствальда - де Ваале с различными значениями реологических параметров для различных интервалов скоростей сдвига.

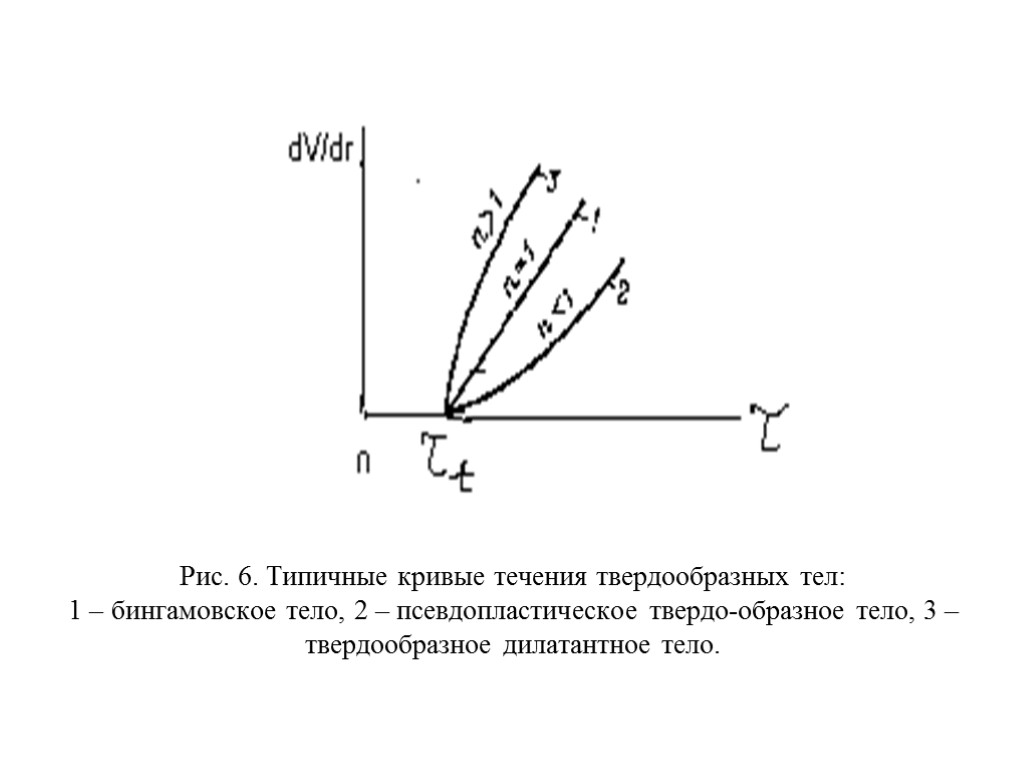
Рис. 6. Типичные кривые течения твердообразных тел: 1 – бингамовское тело, 2 – псевдопластическое твердо-образное тело, 3 – твердообразное дилатантное тело.

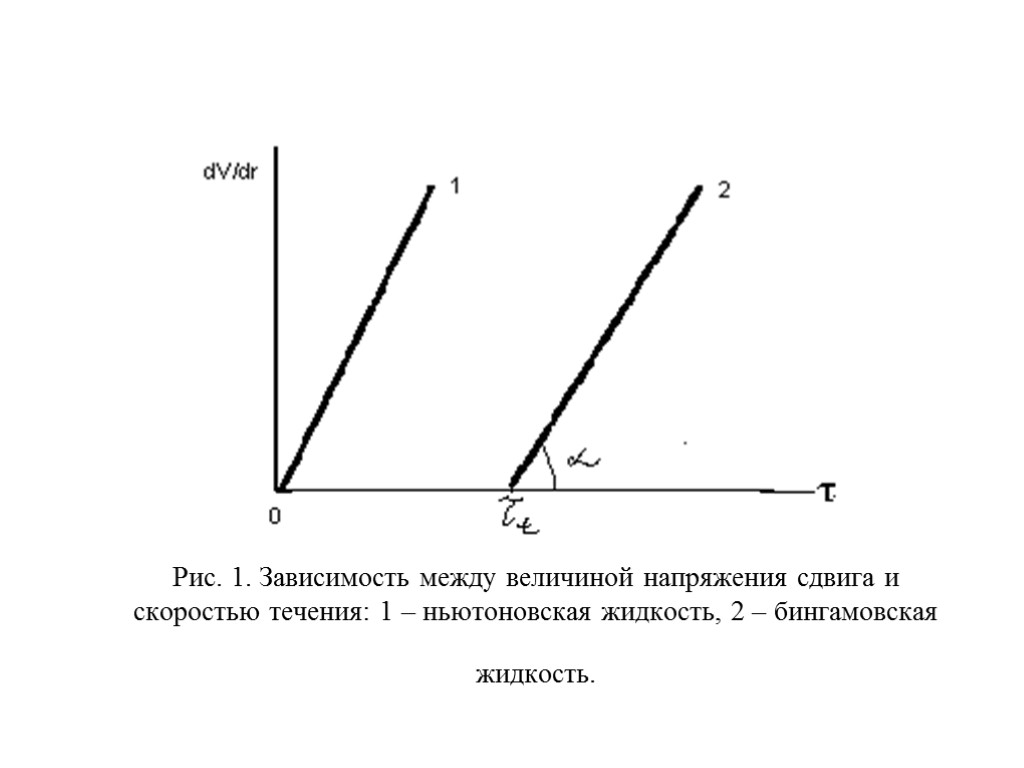
Рис. 1. Зависимость между величиной напряжения сдвига и скоростью течения: 1 – ньютоновская жидкость, 2 – бингамовская жидкость.

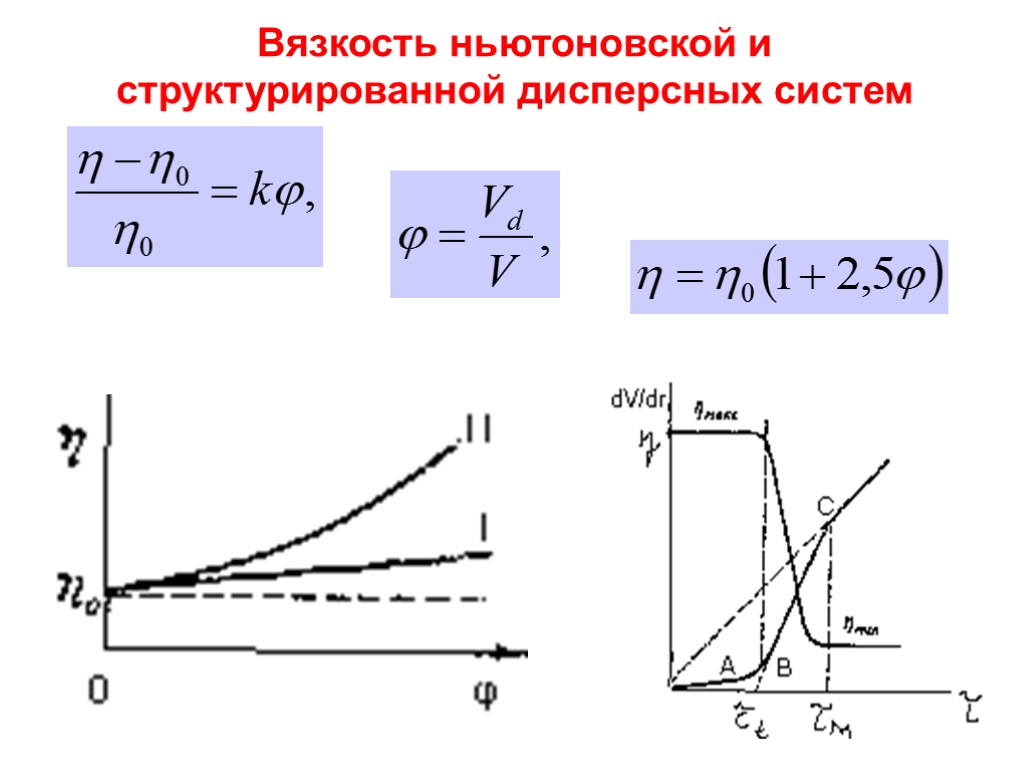
Вязкость ньютоновской и структурированной дисперсных систем

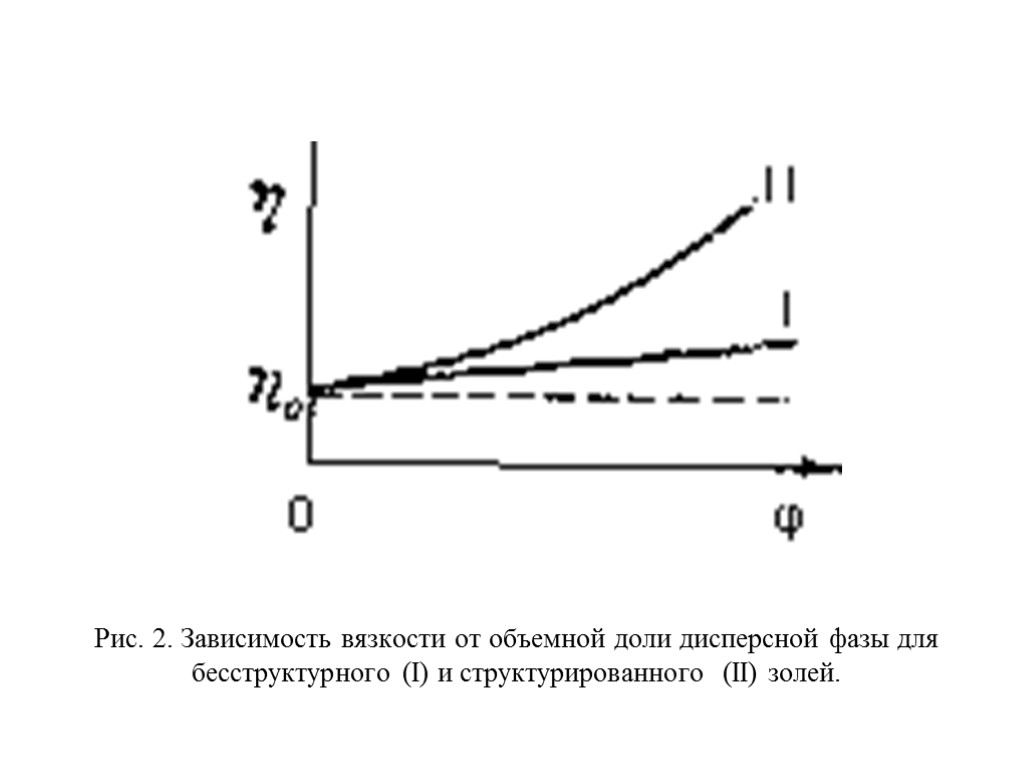
Рис. 2. Зависимость вязкости от объемной доли дисперсной фазы для бесструктурного (I) и структурированного (II) золей.

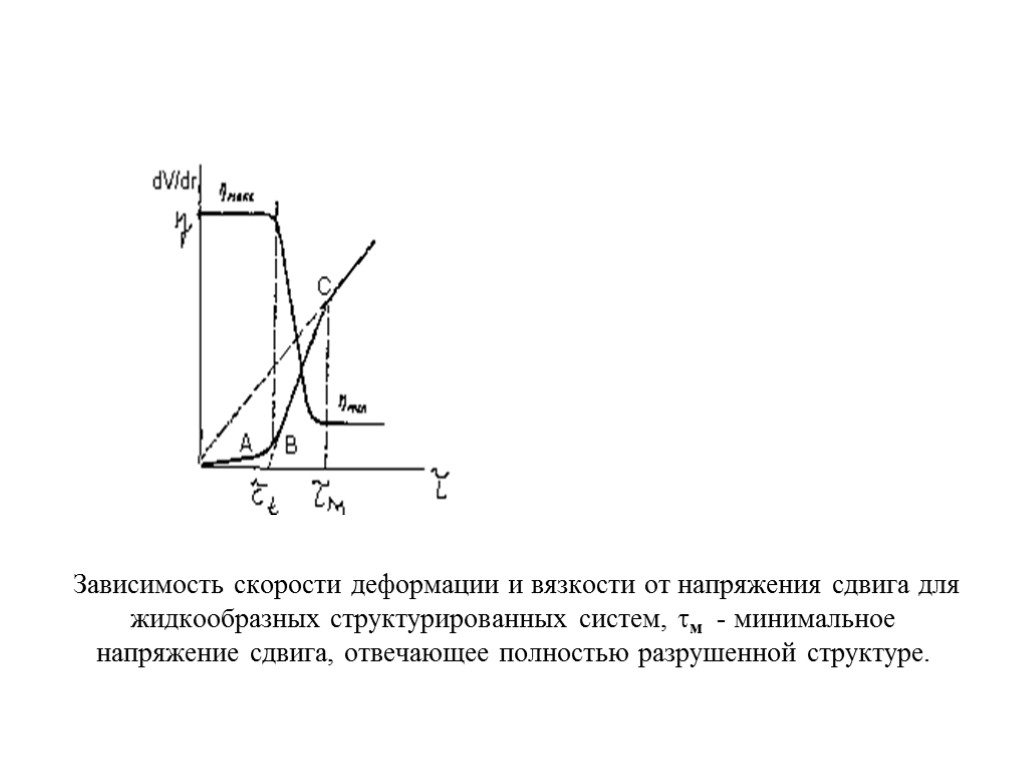
Зависимость скорости деформации и вязкости от напряжения сдвига для жидкообразных структурированных систем, м - минимальное напряжение сдвига, отвечающее полностью разрушенной структуре.

Структурированная ДС Действующее в потоке τ - мало: Поведение частиц ДФ при этом выглядит так: время перемещения частицы от одного конта-кта к другому превышает время установления контакта, связи успевают обратимо восстанавливаться и течение происходит при ненарушенной структуре. Процессы, происходящие в дисперсной системе, напоминают развитие ползучести. Наблюдается медленный рост (dV/dr), причем зависимость между (dV/dr) и  при малом угле α наклона кривой течения к оси напряжений линейная .

Структурированная ДС В этом случае дисперсная система обладает максимальной вязкостью η = ηmax. Когда угол наклона (tg α = (dV/dr) / τ = 1 / ηmax), настолько мал что участок ОА сливается с осью абсцисс, то можно говорить о предельном статическом напряжении сдвига τt, ниже которого тело не течет. Эта величина по смыслу близка к пределу упругости, т.к. при τ < τt структурную сетку можно рассматривать как сплошной статический твердообразный каркас.

Структурированная ДС C ростом касательных напряжений τ в потоке время перемещения частиц ДФ от кантакта к контакту снижается и начинается постепенное разрушение временных контактов между эле-ментами структуры и образование других контак-тов (участок АВ): возникает динамическое равнове-сие, скорость сдвига резко возрастает и реологичес-кая кривая выходит на линейный участок ВС, отра-жающий нарастающее разрушение структуры. Здесь закон течения дисперсной системы описыва-ется уравнением τ = τt + ηп dV/dr. Величина τt находится продолжением прямой ВС до пересечения с осью τ и определяет прочность структуры.

Структурированная ДС В точке С кривой течения, соответствующей пол-ному разрушению структуры дисперсной системы, ее вязкость достигает своего минимального значе-ния ηmin. Величина вязкости при течении может изменяться на несколько порядков: от максимального значения ηmax , отвечающего неразрушенной структуре, до ηmin, характерного для предельно разрушенной структуры. Например, для 10 % – ной суспензии бентонитовой глины величина ηmax достигает значения 106 Па·с , а ηmin - 10-2 Па·с.

Наличие структуры и ее прочность можно оценивать не только величиной статического напряжения сдвига, но и разностью (ηmax - ηmin): чем больше эта разность, тем прочнее струк-тура. • Непрерывный переход от твердообразных тел к жидкообразным может быть осуществлен как с помощью уменьшения τt (уменьшение прочно-сти структуры), так и путем уменьшения разнос-ти между двумя ньютоновскими вязкостями.

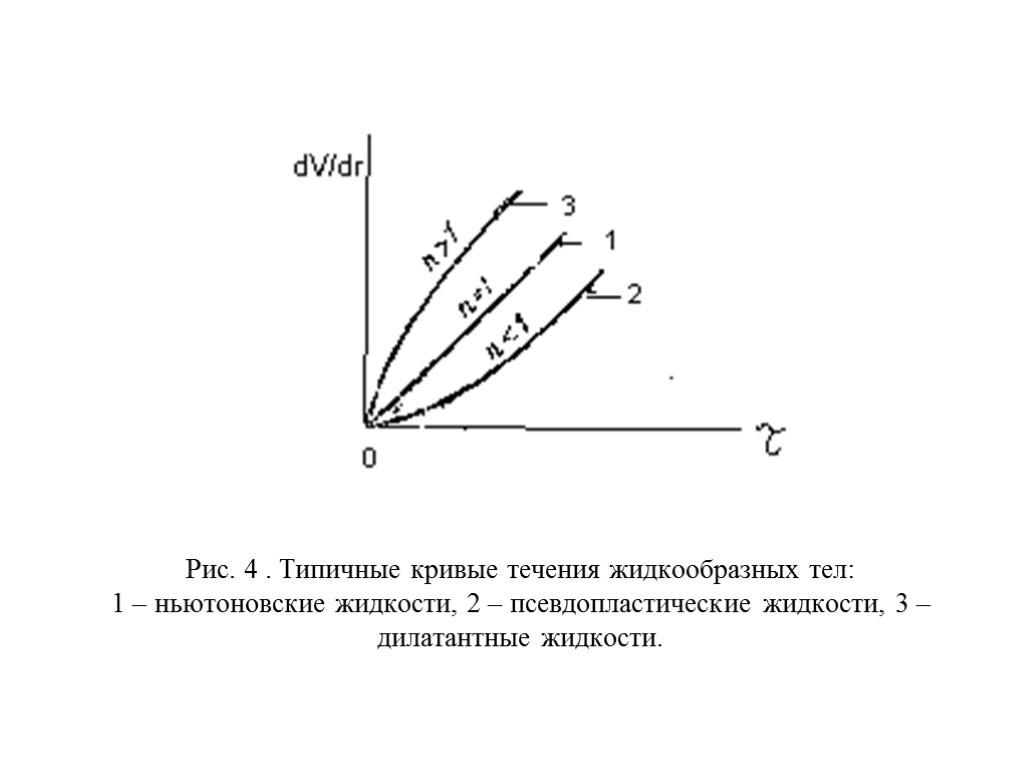
Рис. 4 . Типичные кривые течения жидкообразных тел: 1 – ньютоновские жидкости, 2 – псевдопластические жидкости, 3 – дилатантные жидкости.

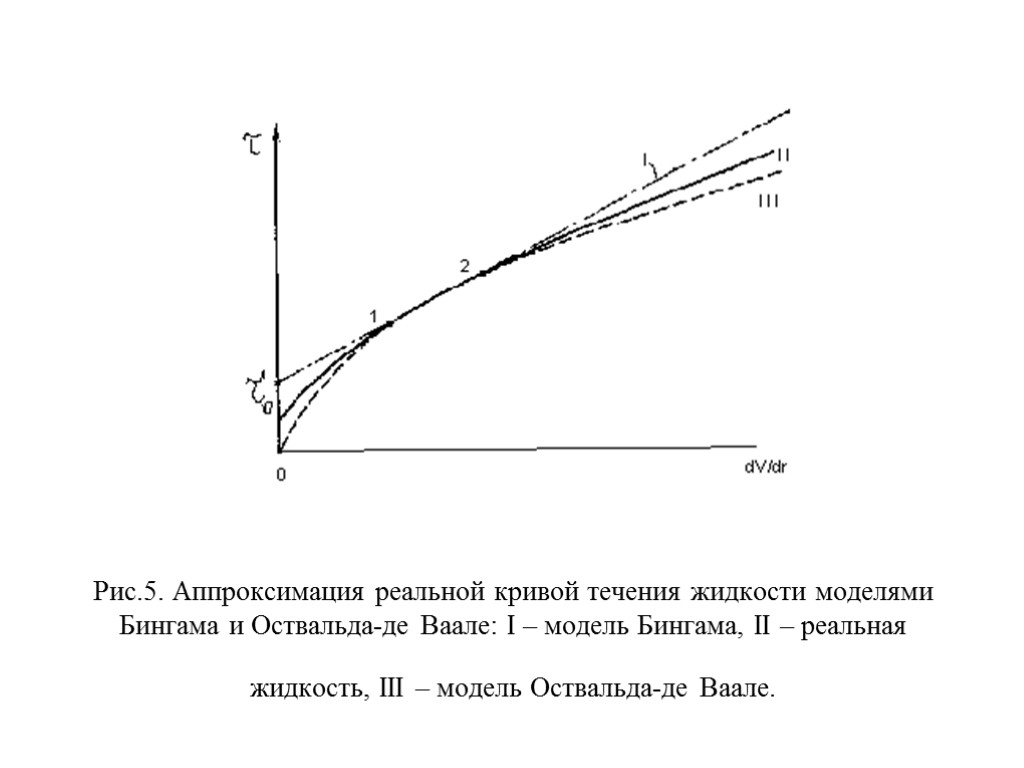
Рис.5. Аппроксимация реальной кривой течения жидкости моделями Бингама и Оствальда-де Ваале: I – модель Бингама, II – реальная жидкость, III – модель Оствальда-де Ваале.

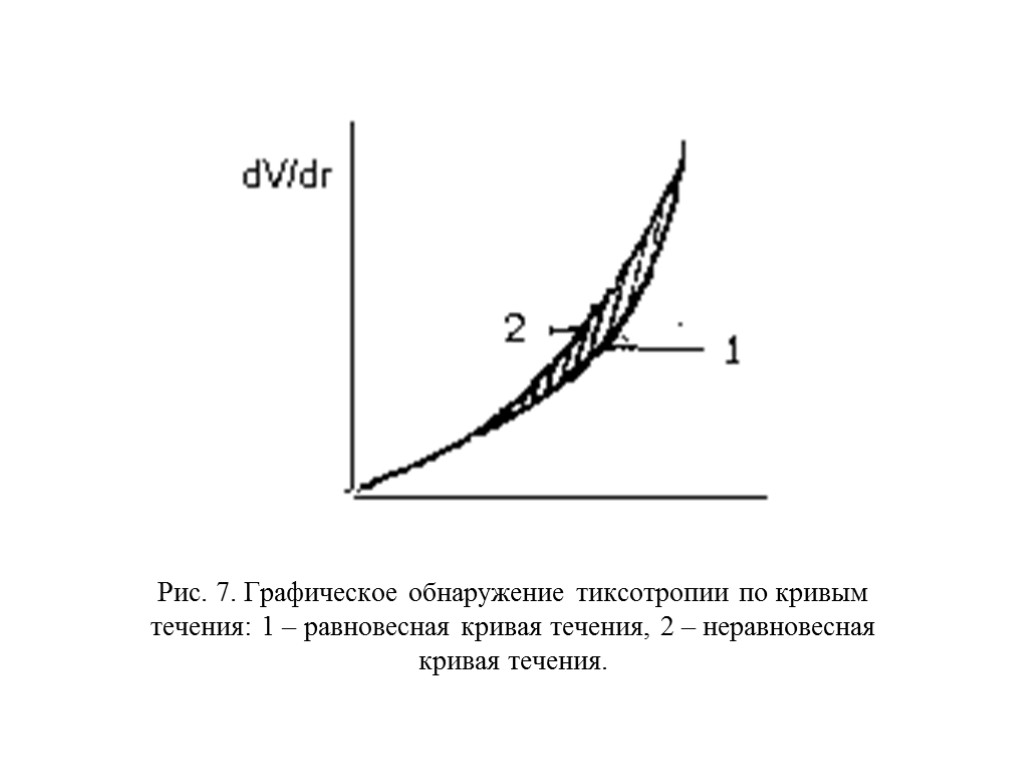
Рис. 7. Графическое обнаружение тиксотропии по кривым течения: 1 – равновесная кривая течения, 2 – неравновесная кривая течения.

Кроме основных показателей моделей Бингама – Шведова и Оствальда – де Ваале (Т, , k, n), для ха-рактеристики реолоических свойств буровых раство-ров в последние годы широко используют и допол-нительные показатели: коэффициент пластичности; эффективную вязкость при скорости сдвига равной 100 с-1; асимптотическую вязкость или эффективную вязкость при полностью разрушенной структуре (при скорости сдвига равной 10000 с-1).

Коэффициент пластичности бурового раствора (КП, с-1) определяется величиной отношения динамичес-кого напряжения сдвига к пластической вязкости КП = T / П. С ростом коэффициента пластичности увеличивается транспортирующая способность потока, а также гидроди-намическое давление струй бурового раствора, выходя-щих из насадок долота, что обеспечивает более эффек-тивное разрушение горных пород на забое и рост механи-ческой скорости бурения. При этом высокие значения коэффициента пластичности нужно поддерживать за счет снижения пластической вязкости бурового раствора, а не увеличения его динамического напряжения сдвига.

Эффективная вязкость характеризует ту действи-тельную вязкость, которой обладает буровой раст-вор при скорости сдвига, имеющей место в кольце-вом пространстве скважины, в бурильных трубах или в промывочных каналах породоразрушающего инструмента (в насадках долота). Эффективная вязкость при скорости сдвига, равной 100 с-1 (ЭВ100, Пас), характеризует вязкость бурового раствора в кольцевом пространстве скважины и яв-ляется основным показателем, определяющим тран-спортирующую способность его потока, которая тем выше, чем выше значения ЭВ100. ЭВ100 = k (100)n - 1.

С ростом ЭВ100 увеличиваются гидравличес-кие сопротивления при течении бурового рас-твора в кольцевом пространстве и, соответ-ственно, дифференциальное давление, что ведет к снижению механической скорости бу-рения и проходки на долото в результате не только удержания частиц разрушенной поро-ды на забое, но и ухудшения условий форми-рования зоны предразрушения (условий за-рождения и развития макро- и микротрещин).

Эффективная вязкость при полностью разрушен-ной структуре (ЭВ10000) характеризует вязкость буро-вого раствора в насадках долот и в песко- илоотде-лителях (гидроциклонах). С уменьшением ЭВ10000 повышается степень очи-стки забоя скважины от шлама и степень охлаждения вооружения долота, вследствие чего возрастает ре-сурс его работы и механическая скорость бурения. Кроме того, с уменьшением ЭВ10000 снижается ин-тенсивность обогащения бурового раствора шламом, так как при меньшей вязкости последний легче отде-ляется в очистных устройствах. ЭВ10000 = k (10000) n - 1.

Использование семи показателей (0, , k, n, КП, ЭВ100, ЭВ10000) позволяет достаточно всесторонне оха-рактеризовать реологические свойства и связанные с ними функциональные возможности бурового раст-вора. На этапе проектирования бурового раствора это яв-ляется достоинством, но в процессе эксплуатации раствора становится недостатком: одновременно контролировать большое число показателей, а глав-ное управлять ими, чрезвычайно сложно.

Реопектные ДС Реопектные дисперсные системы в буре-нии не используются, т.к. таким систе-мам свойственно структурирование при сдвиге: сдвиговое воздействие - катали-затор твердообразования. Пример: 42 % - ный водный раствор гипса (1 - 10) мкм после встряхивания затвердевает после 10 минут покоя. Но если пробирку с этим раствором пе-рекатывать между ладонями, то время затвердевания сократится до 20 секунд.

Нестационарные дисперсные системы Тиксотропные ДС Тиксотропия - свойство коагуляционных структур восстанавливать контакты между частицами дис-персной фазы. Восстановление структуры контроли-руется по увеличению вязкости системы, СНС. Тиксотропия - уменьшение вязкости ДС во времени при наложении нагрузки и постепенный рост вязкости после снятия нагрузки.

Тиксотропные дисперсные системы Тиксотропия характерна для свободнодиспер-сных дисперсных систем, в которых частицы дисперсной фазы несут на себе электрический заряд и стремятся занять положение, соответ-ствующее минимуму потенциальной энергии. При этом частицы ориентированы в определен-ных направлениях, образуя прочную структуру, способную сопротивляться разрушению до оп-ределенного значения касательного напряжения τt . Величина τt зависит от природы и концент-рации твердой фазы в дисперсной системе, тем-пературы, давления, наличия электролитов в дисперсионной среде, от длительности состо-яния покоя.

Тиксотропные дисперсные системы Реологически нестационарным тиксотропным жидкостям свойственна функциональная зависимость τ = τ(dV/dr, t), где t – время (время действия напряжений, время между циклами нагружения дисперсной системы). Считается, что жидкость обладает памятью своей истории: напряжение, замеренное в определенный момент времени, зависит не только от скорости деформирования в данный момент, но и от предшествующего деформированного состояния.

Тиксотропные дисперсные системы Примером тиксотропной системы является суспен-зия бентонитовой глины: при 10 % - ной концент-рации дисперсной фазы суспензия утрачивает те-кучесть, застывает и приобретает упругие свойства. Но после ее встряхивания она вновь полностью разжижается. Если ее оставить в покое, то через время θ (тиксотропный период) бентонитовая сус-пензия вновь станет твердообразной. Для учета ха-рактера тиксотропных изменений принято изме-рять величину τt дважды: через 1 минуту и через 10 минут.

Тиксотропия Буровой раствор должен обладать тиксотроп-ными свойствами с малым периодом θ , ина-че при остановке насоса выбуренная горная порода начнет оседать и вызовет прихват бу-рового инструмента. Тиксотропный раствор в этих случаях твердеет и удерживает шлам, но раствор разжижается, когда насос начина-ет работать.

Тиксотропные дисперсные системы Рост СНС растворов после прекращения циркуляции в скважине замедляет или прекращает оседание шлама, что снижает вероятность прихвата. Рост СНС растворов в отстойниках ЦС затрудняет их очистку от шлама