Rent Lease or Buy Randomized Algorithms for Multislope

Rent, Lease or Buy: Randomized Algorithms for Multislope Ski Rental Zvi Lotker Ben-Gurion University Boaz Patt-Shamir Dror Rawitz Tel Aviv University

Rent or Buy Dilemma the sleeping Baby Problem: n You finally managed to put baby to sleep n Baby will wake up at some unknown time n Should parent stay awake or go to sleep? n n – Going to sleep incurs some fixed effort – Staying awake incurs an effort per time unit

Rent or Buy Dilemma n Question: n n Competitive Analysis: n n n How do we measure the quality of our solution Worst case analysis: Baby will try to make parent’s life hard Compare our solution to n best possible solution

Rent or Buy n Classical Ski Rental: n n n – – – Vacation at ski resort End of vacation is unknown Cost of skis is €B, rent is € 1/day Should we rent or buy the skis? When should we buy? Optimal offline cost:

Optimal Online Strategies: 2 -competitive deterministic strategy [Karlin et al. 88] n -competitive randomized strategy [Karlin et al. 94] n What if the second option is not const? n

General two slope n Assume that we can chose: n n To rent or to buy hose But even when we by the hose we need to pay the property tax 1+(1 -r)-competitive deterministic strategy n -competitive randomized strategy n

Deterministic strategy n If the end of the game is at t<1 n n If the end of the game is at t>1 n n Opt cost r·t+(1 -r) Assume the game end at the time online move to the second option n n Opt cost t In this case online cost is t+1 -r So the competitive is

Ski rental rate due towith two general options investment in buying slope 2 n i n third term is due to being at slope 2 Let p (t) be the probability that the algorithm is using slope i=1, 2 The expected rate in which the algorithm spends money is

How we find c n n At time t>1, optimal strategy spends money at rate a Assume that the online stop buying

Interpretation of the algorithm n We pick an random time according to P 2 n n n If this number is bigger than 1 we do not move to the second option If this number is less then 1 we buy the second option at that time. Example assume that r=0. 3, c=1. 34683

Optimality of the algorithm n We use Yao’s Lemma We assume that the game end at time t with the prob n The optimal expected cost is n

Optimality of the algorithm n n Assume that Ax is a deterministic algorithm that end x them the expected cost of Ax is 1, for 0<x<1 Therefore the competitive is

Rent, Lease or Buy n Housing costs game: n n n Price of house/apartment increases closer to city center Transportation rates decrease closer to city center Extended Ski Rental: n n Mixed rent and buy options Pure buy or pure rent may not exist

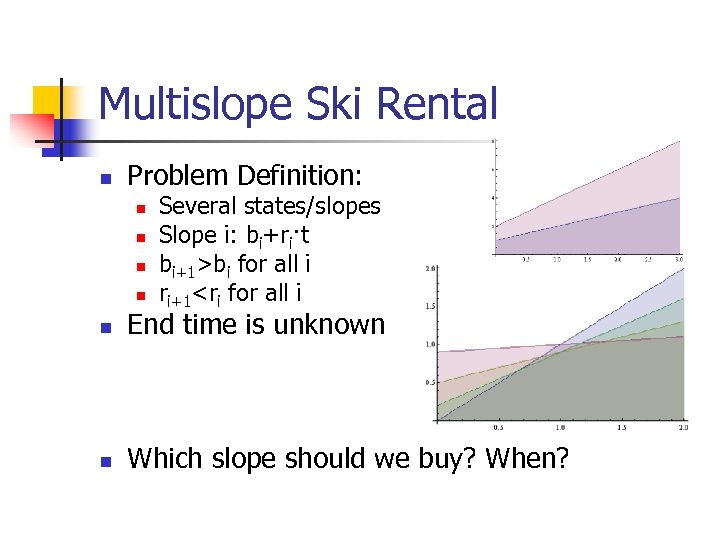
Multislope Ski Rental n Problem Definition: n n Several states/slopes Slope i: bi+ri·t bi+1>bi for all i ri+1<ri for all i n End time is unknown n Which slope should we buy? When?

Multislope Ski Rental n n Online Buying Costs: Say we are in slope i, how much do we pay for slope j n n n Additive Model: bj−bi Non-Additive Model: bij “From scratch”: bj

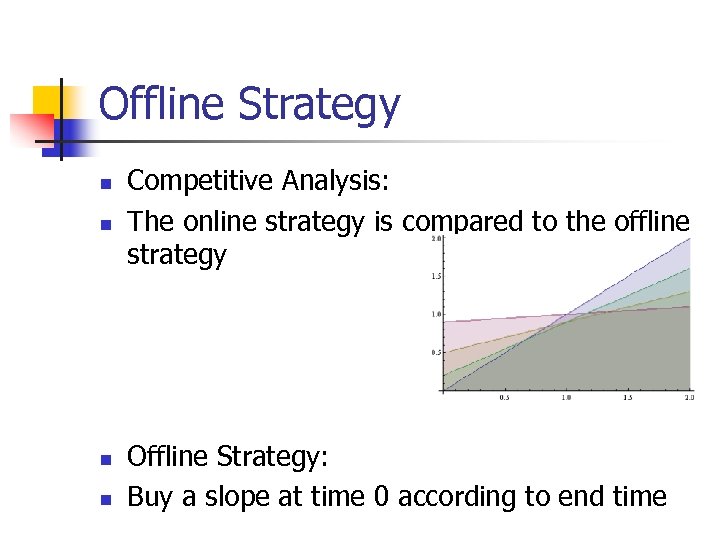
Offline Strategy n n Competitive Analysis: The online strategy is compared to the offline strategy Offline Strategy: Buy a slope at time 0 according to end time

Previous Results & Applications n Online Capital Investments: n n n Deterministic 6. 83 -competitive strategy (slopes may arrive over time) [Azar et al. 99] Deterministic lower bound 3. 618 Randomized 2. 88 -competitive strategy [Damaschke 03] Rerouting in ATM networks: 4 -competitive strategy (slopes may be concave) [BCN 00]

Previous Results & Energy Saving n Slopes are hibernation modes n n Deterministic 2 -competitive strategy for additive model [IGS 02] Algorithm that computes best deterministic strategy for non-additive model [AIS 04]

Our Results n Additive Model: n n n Randomized e/(e− 1) competitive strategy (e−rk/r 0)/(e− 1) when rk >0 Decomposition into k classical ski rental instances Strategy is combination of k strategies Main Result: n Algorithm that computes best randomized strategy

Profiles Costs n Expected rent at time t: n Expected total rental cost at time t: n Expected buying cost at time t: n Total: Expected cost at time t:

diff. equations n The problem we want by solve is to This can approximate by lp

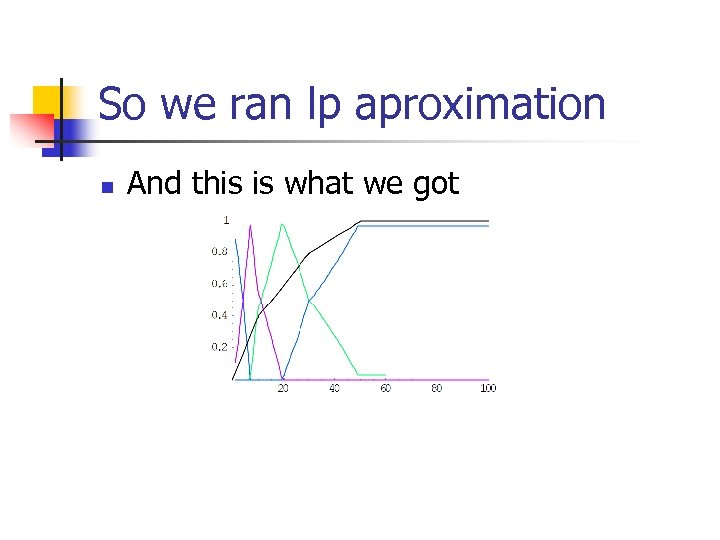
So we ran lp aproximation n And this is what we got

Strategies & Profiles n Randomized Startegy: n n Randomized Profile: n n n Additive model: we go from slope i to slope i + 1 When do we move to the next slope? Probability distribution over deterministic strategies pi(t) – probability of being in slope i at time t Σipi(t) = 1 for all t≥ 0 Plan: Every strategy induces a profile Find best profile Construct strategy

Optimal Profiles n Chain of Transformations: n n Optimal profile Continuous optimal profile Continuous in t Prudent optimal profile Only one or two consecutive active slopes Tight optimal profile Moves to the next slope as soon as possible

Prudent Profiles n n Continuous to Prudent: for all t two consecutive slopes are determined n n n Buying cost is preserved ⇛ Rent may only decrease ⇛ Continuity is preserved

Prudent to Tight n Tight: Buy next slope as soon as possible n n ⇛ Rent may only decrease Theorem: There exists a tight optimal profile

Computing Tight Profile n Computing tight profile for a given c: n Solve diff. equations: n For tight profiles: n We assume that we know c and then we solve all those diff. equations n n If we solve all of them before time 1 we can make c small If not we have to make c bigger

Algorithm n n Computing a Strategy: Let p be a tight profile X~U(0, 1) Move from slope i to slope i + 1 when Theorem: Randomized (c + ε)-competitive strategy can be found in O(k log 1/ε), where c is the best possible ratio

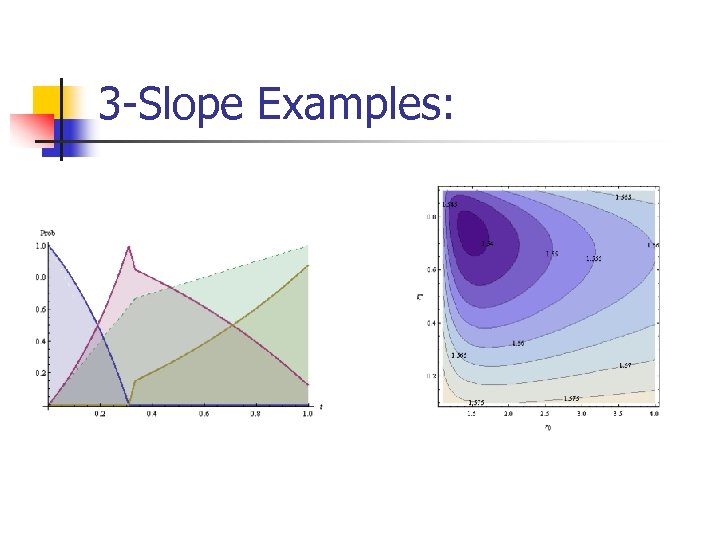
3 -Slope Examples:

An 1. 581 Competitive Algorithm n Assume rk=0 n n Let b’ 0=0; r’i 0=ri-1 -ri; b’i 1=bi-bi-1; r’i 1=0 Let Opti(t) be the offline alg for ski prob {(b 0 i, r 0 i), (b 1 i, r 1 i)} Lemma Opt(t)=Σ Opti(t) Proof:

An 1. 581 Competitive Algorithm n We solve each problem separate n n Let P 0 i(t), P 1 i(t) be the solution. We define the profile for the multislope: n n Pi(t)= P 1 i(t)- P 1 i+1(t) for i=1, …, k-1 P 0(t)= P 01(t), Pk(t)= P 1 k(t)

An 1. 581 Competitive Algorithm n We solve each problem separate n Let P 0 i(t), P 1 i(t) be the solution. Lemma P 1 i-1(t)≥P 1 i(t) n Proof P 1 i(t)=Exp[b 1 i/r 0 i] now b 1 i/r 0 i>b 1 i-1/r 0 i-1 n n It is clear that the sum of all prob is 1.

An 1. 581 Competitive Algorithm n n n Given P one can obtain an online strategy whose profile is P. let U~U[0, 1] we move from state i to state i + 1 when U=P 1 i(t) for every state i

An 1. 581 Competitive Algorithm n n n Theorem The competitive ratio of P is: e/(e− 1) Proof: expected cost to the combined strategy is the sum of the costs to the two-slope strategies n n n buying cost is ΣBPi(t) Ranting cost is Σr. Pi(t) By the fact that each of the strategies is e/(e-1) competitive the lemma follows.

Open Problems: n n Compute best randomized strategy for non-additive model What is the get LP for homogeneous differential equation.

C: UsersuserDocumentsZviold2007sky k