Rendezvous Planning in Mobilityassisted Wireless Sensor Networks Guoliang

Rendezvous Planning in Mobilityassisted Wireless Sensor Networks Guoliang Xing; Tian Wang; Zhihui Xie; Weijia Jia Department of Computer Science City University of Hong Kong

Agenda • Motivation • Problem formulation • Rendezvous planning algorithms – Without data aggregation – With data aggregation • Performance evaluation • Other projects

Wireless Sensor Networks physical environments: homes/offices Structural monitoring Industrial automation (Golden gate bridge, SF) (Intel fabrication plant) Healthcare (Boston Medical Center) Pervasive computing • Market – “US $100 M in 2005, $500 M by 2010”, Kris Pister, CEO of Dust Networks, Professor of UC Berkeley • Challenges – Limited power supplies: batteries, small solar panels – Long lifetime requirements: months to tens of years – Must minimize network power consumption

Challenges for Data-intensive Sensing Applications • Many applications are data-intensive – Structural health monitoring • Accelerometers sample at 100 Hz – Micro-climate and habitat monitoring • Mics/cameras generate a few K bytes every minute • Multi-hop wireless relays are power-consuming – A Mica 2 mote can only transmit a couple days • A tension exists between the sheer amount of data generated and limited power supply

Mobility-assisted Data Collection • Mobile nodes move close to sensors and collect data via short-range communications – Mobile nodes can transport data mechanically • Mobile nodes are less power-constrained – Can move to wired power sources • Number of wireless relays is reduced

Mobile Sensor Platforms Networked Infomechanical Systems Robomote @ USC [Dantu 05 robomote] (NIMS) @ CENS, UCLA XYZ @ Yale http: //www. eng. yale. edu/ enalab/XYZ/ • Low movement speed (0. 1~2 m/s) – Increased latency of data collection – Reduced network capacity

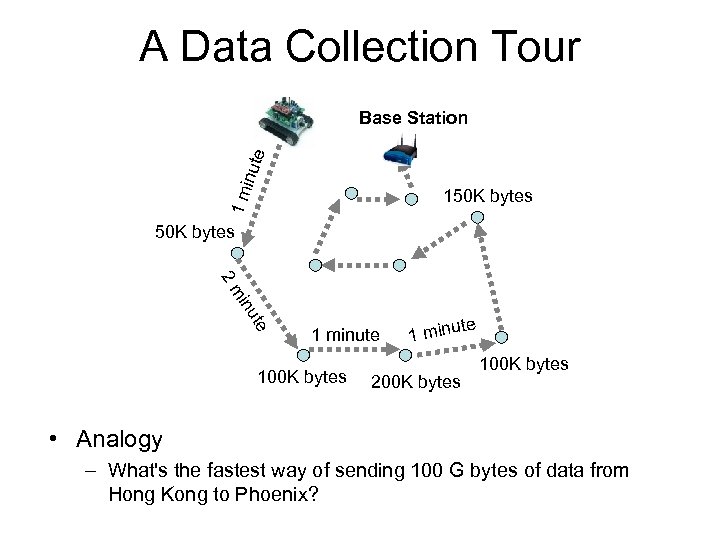
A Data Collection Tour inut e Base Station 1 m 150 K bytes te inu 2 m 1 minute 100 K bytes te 1 minu 200 K bytes 100 K bytes • Analogy – What's the fastest way of sending 100 G bytes of data from Hong Kong to Phoenix?

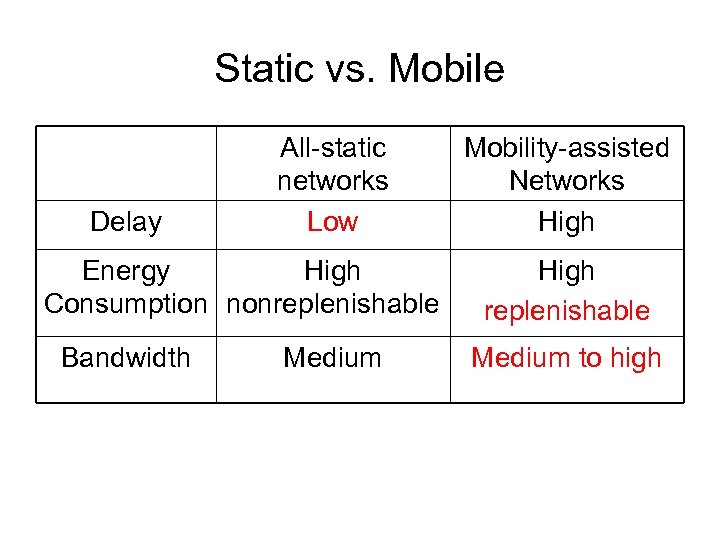
Static vs. Mobile Delay All-static networks Low Energy High Consumption nonreplenishable Bandwidth Medium Mobility-assisted Networks High replenishable Medium to high

Rendezvous-based Data Collection • Some nodes serve as “rendezvous points” (RPs) – Other nodes send their data to the closest RP – Mobiles visit RPs and transport data to base station • Advantages – In-network caching + controlled mobility – Mobiles can collect a large volume of data at a time – Minimize disruptions due to mobility • Mobiles contact static nodes at RPs at scheduled time

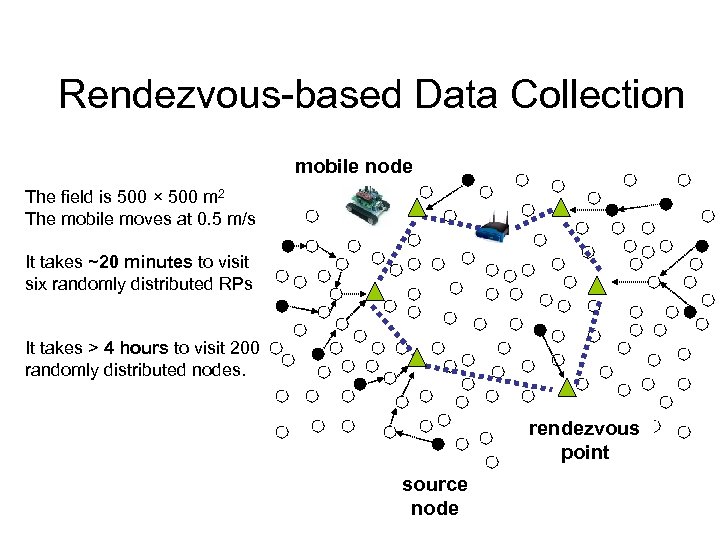
Rendezvous-based Data Collection mobile node The field is 500 × 500 m 2 The mobile moves at 0. 5 m/s It takes ~20 minutes to visit six randomly distributed RPs It takes > 4 hours to visit 200 randomly distributed nodes. rendezvous point source node

The Rendezvous Planning Problem • Total network energy of transmitting data from sources to RPs is minimized • Choose RPs s. t. mobile nodes can visit all RPs within data collection deadline • Joint optimization of positions of RPs, motion paths of mobile, and routing paths of data

Assumptions • • Only one mobile is available Mobile moves at a constant speed v Mobile picks up data at locations of nodes Data collection deadline is D – User requirement: “report every 10 minutes and the data is sampled every 10 seconds” – Recharging period: e. g. , Robomotes powered by 2 AA batteries recharge every ~30 minutes

Data Aggregation • Data from different sources can be aggregated – Reduces the amount of network traffic – "what's the lowest temperature of this region"? • Without aggregation – Optimal routing tree is the shortest path tree • With aggregation – Optimal routing tree is the minimum spanning/Steiner tree

Agenda • Motivation • Problem formulation • Rendezvous planning algorithms – Without data aggregation – With data aggregation • Performance evaluation • Other projects

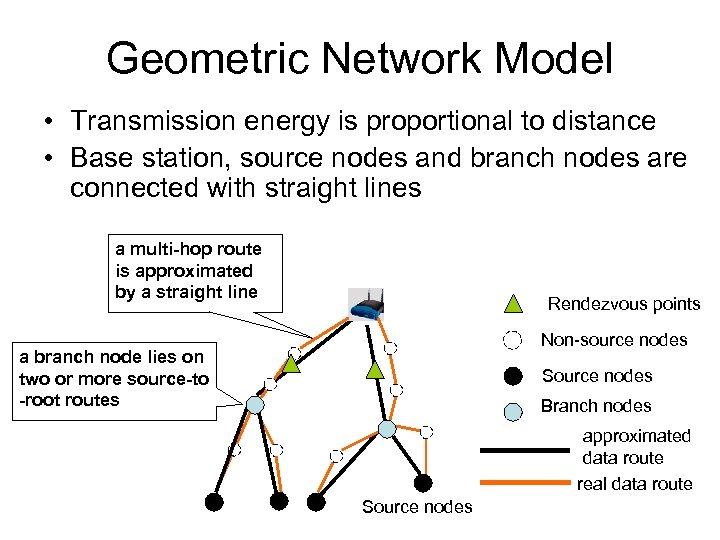
Geometric Network Model • Transmission energy is proportional to distance • Base station, source nodes and branch nodes are connected with straight lines a multi-hop route is approximated by a straight line Rendezvous points Non-source nodes a branch node lies on two or more source-to -root routes Source nodes Branch nodes approximated data route real data route Source nodes

Problem Formulation • Given a tree T(V, E) rooted at B and sources {si}, find RPs, {Ri}, s. t. , the tour visiting {B}U{Ri} is no longer than L=v. D and d. T(si, Ri) – the on-tree distance between si and Ri • The problem is NP-hard (reduction from the Traveling Salesman Problem)

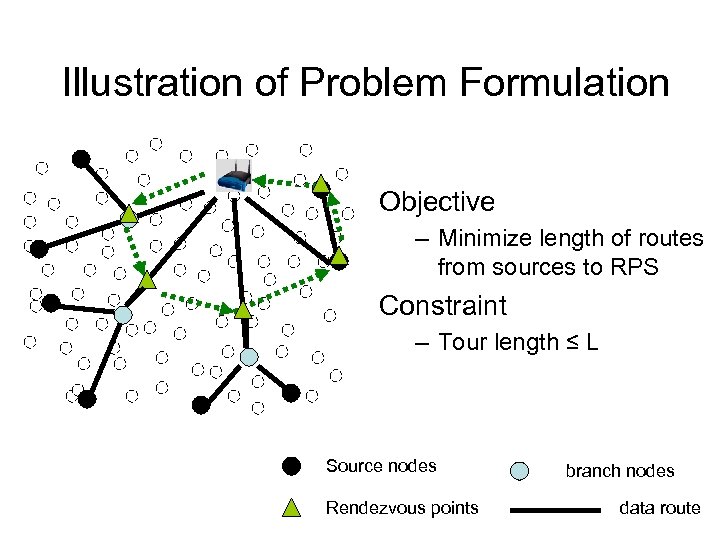
Illustration of Problem Formulation Objective – Minimize length of routes from sources to RPS Constraint – Tour length ≤ L Source nodes Rendezvous points branch nodes data route

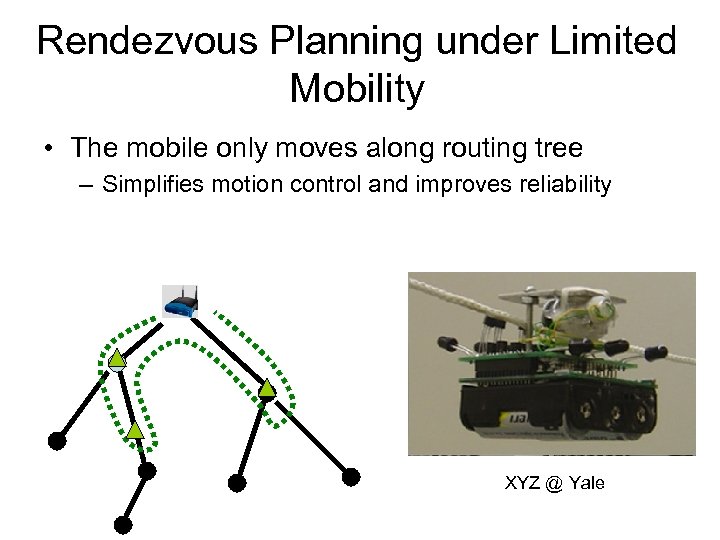
Rendezvous Planning under Limited Mobility • The mobile only moves along routing tree – Simplifies motion control and improves reliability XYZ @ Yale

An Optimal Algorithm • Sort edges in the descending order of the number of sources in descendents • Choose a subset of (partial) edges from the sorted list whose length is L/2 • The mobile tour is the pre-order traversal of the chosen edges

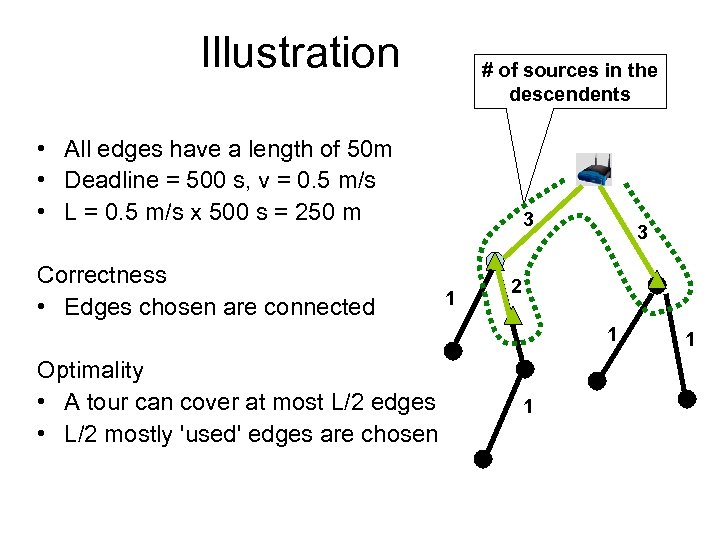
Illustration # of sources in the descendents • All edges have a length of 50 m • Deadline = 500 s, v = 0. 5 m/s • L = 0. 5 m/s x 500 s = 250 m Correctness • Edges chosen are connected 3 1 3 2 1 Optimality • A tour can cover at most L/2 edges • L/2 mostly 'used' edges are chosen 1 1

A Heuristic for Unlimited Mobility • In each iteration, choose the RP candidate with the max utility defined by c(x) • Terminate if no more RPs can be chosen or all sources become RPs the decreased length of data routes TSP(W) computes the distance to visit nodes in W using a Traveling Salesman Problem solver the increased length of the mobile node tour

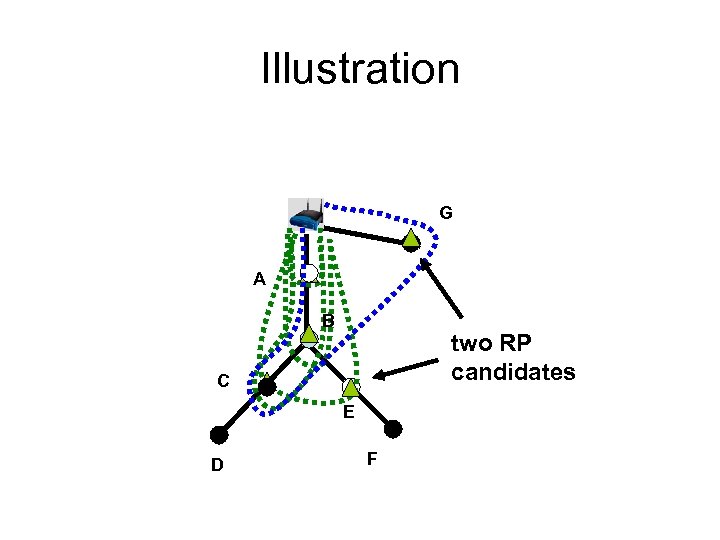
Illustration G A B two RP candidates C E D F

Agenda • Motivation • Problem formulation • Rendezvous planning algorithms – Without data aggregation – With data aggregation • Protocol design • Performance evaluation • Other projects

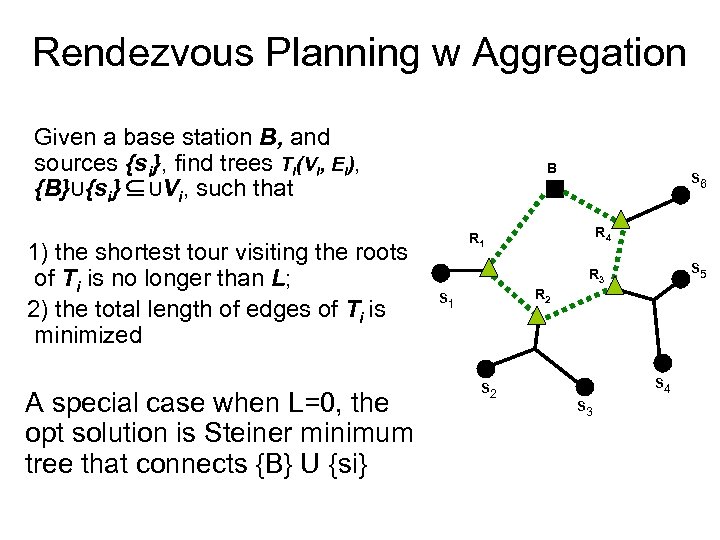
Rendezvous Planning w Aggregation Given a base station B, and sources {si}, find trees Ti(Vi, Ei), {B}U{si} Í UVi, such that 1) the shortest tour visiting the roots of Ti is no longer than L; 2) the total length of edges of Ti is minimized A special case when L=0, the opt solution is Steiner minimum tree that connects {B} U {si} B s 6 R 4 R 1 s 5 R 3 R 2 s 1 s 2 s 3 s 4

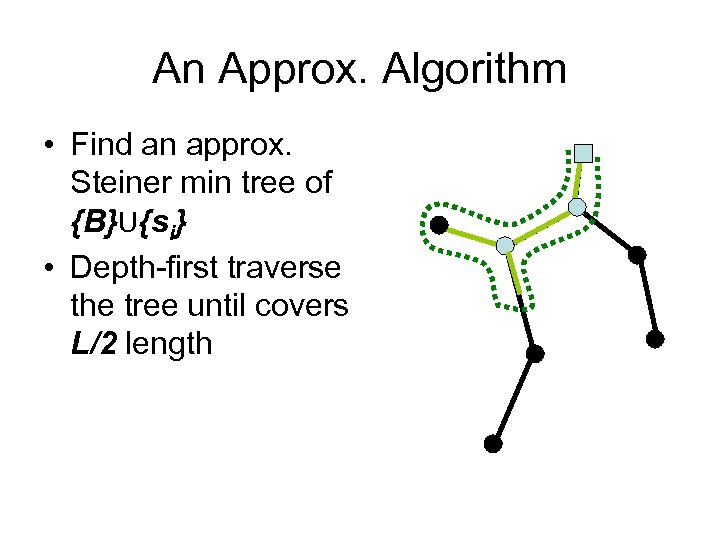
An Approx. Algorithm • Find an approx. Steiner min tree of {B}U{si} • Depth-first traverse the tree until covers L/2 length

The Improved Algorithm 1. Find T - an approx. Steiner min tree of {B}U{si} 2. Y=L/2; 3. Depth-first traverse T from B until cover Y length, denote I as the set of intersections 5. if X = L − TSP(I) > δ Y=Y+X/2; goto 3; else exit; TSP(R) – the length of tour visiting points in R, computed by a Traveling Salesman Problem solver

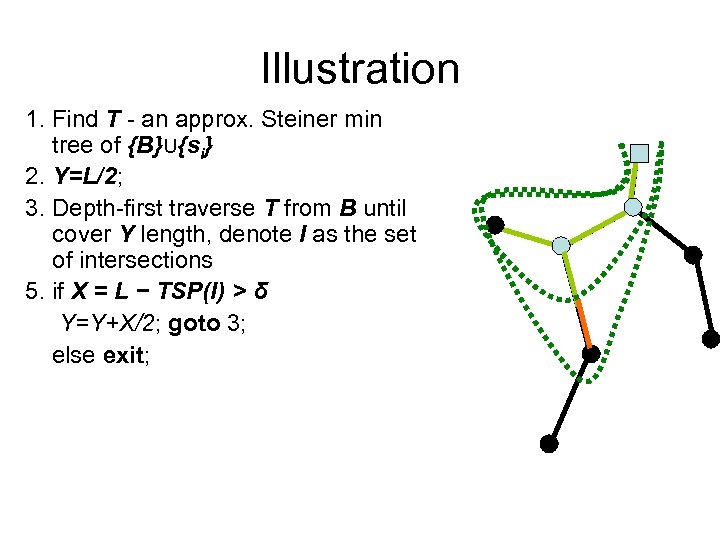
Illustration 1. Find T - an approx. Steiner min tree of {B}U{si} 2. Y=L/2; 3. Depth-first traverse T from B until cover Y length, denote I as the set of intersections 5. if X = L − TSP(I) > δ Y=Y+X/2; goto 3; else exit;

Approx. Ratio • The approximation ratio of the algorithm is α+β(2α-1)/2(1 -β) – α is the best approximation ratio of the Steiner Minimum Tree problem – β = L/SMT({B} U {si})

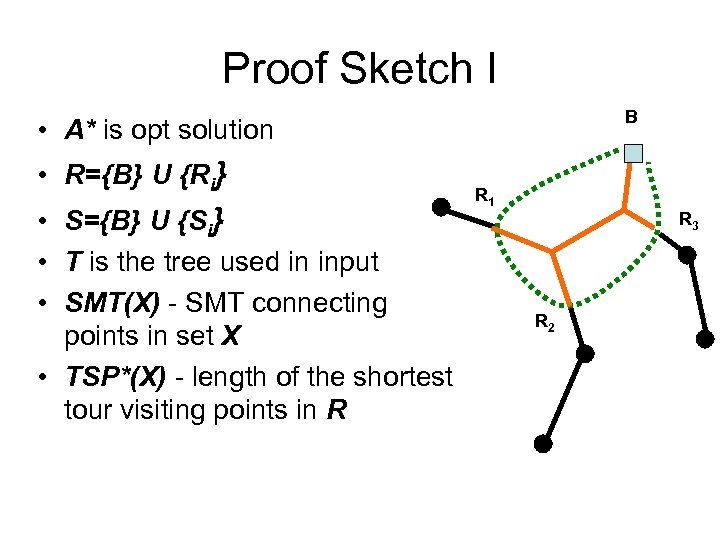
Proof Sketch I B • A* is opt solution • R={B} U {Ri} • S={B} U {Si} • T is the tree used in input • SMT(X) - SMT connecting points in set X • TSP*(X) - length of the shortest tour visiting points in R R 1 R 3 R 2

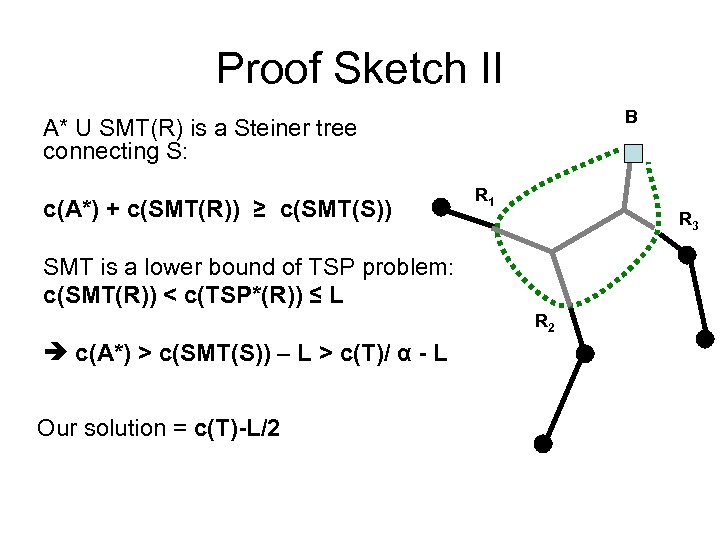
Proof Sketch II B A* U SMT(R) is a Steiner tree connecting S: c(A*) + c(SMT(R)) ≥ c(SMT(S)) R 1 R 3 SMT is a lower bound of TSP problem: c(SMT(R)) < c(TSP*(R)) ≤ L R 2 c(A*) > c(SMT(S)) – L > c(T)/ α - L Our solution = c(T)-L/2

Simulation Settings • 100 sources are randomly distributed in a 300 m X 300 m field, base station is on the left corner • Each source generates 2 bytes/second, delivery deadline is 20 minutes • Implemented USC model [Zuniga et al. 04] to simulate lossy links on Mica 2 motes • Baseline algorithms – – – – NET: collect data via the routing tree without using mobile nodes Sector: mobile moves on a sector of 45 o RP-CP: the optimal algorithm with limited mobility RP-UG: the utility-based heuristic RP-SRC: choose a subset of sources as RP-Agg: the basic algorithm with aggregation RP-Agg*: the improved algorithm with aggregation

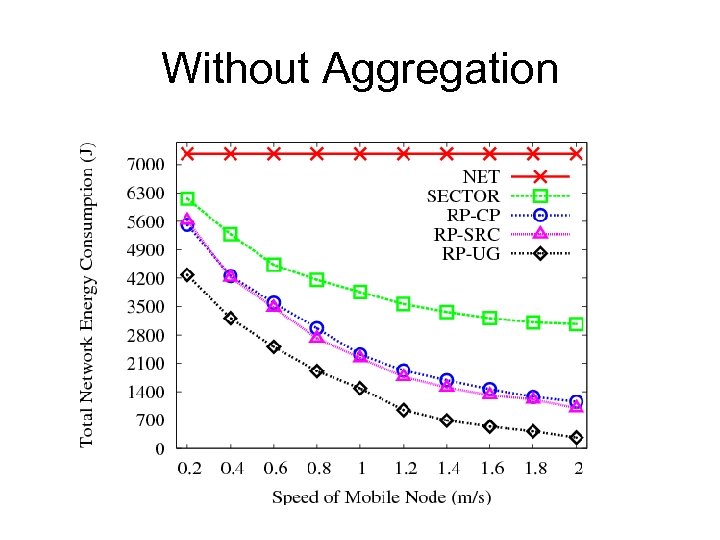
Without Aggregation

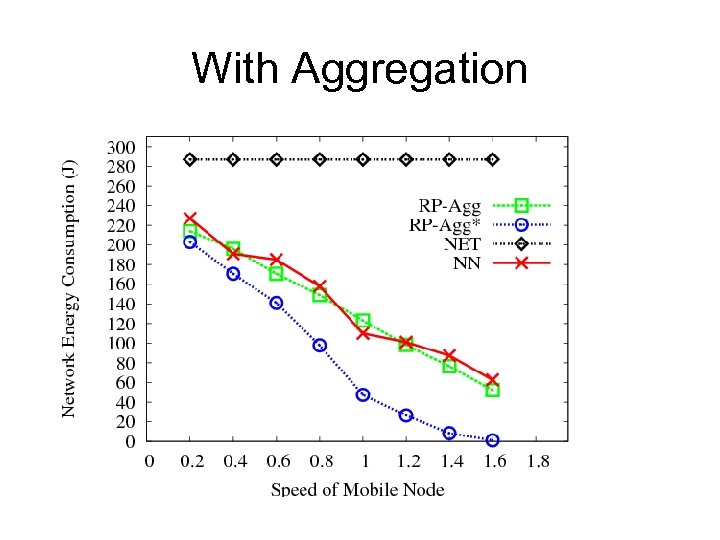
With Aggregation

Recent Projects • Rendezvous Planning in Mobility-assisted Wireless Sensor Networks, – 28 th IEEE Real-Time Systems Symposium (RTSS), 2007, acceptance ratio 44/171=25. 7% • Dynamic multi-resolution data dissemination – 10 th ACM/IEEE International Symposium on Modeling, Analysis and Simulation of Wireless and Mobile Systems (MSWi. M), 2007, acceptance ratio 41/161=24. 8% • Unified Radio Power Management Architecture – International Symposium on Information Processing in Sensor Networks (IPSN), 2007, acceptance ratio 38/170=22. 3%

Challenges of Data Dissemination • Queries have different temporal resolutions – "report temperature readings every 1 minute" – "report light readings every 2 minutes" • Queries are dynamic – New queries can arrive anytime – Data rates of existing queries can change – Optimal data dissemination tree is not fixed!

Impact of Data Rate (Resolution) • Data rate determines total power cost – Radio power cost varies in different states • Tx: 106. 8, Rx/Idle: 32, Sleeping: 0. 001 m. W (cc 1000) – Energy cost is sum of power cost in each state weighted by the time in the state • Exploring diversity of data rates reduces power due to broadcast wireless channel

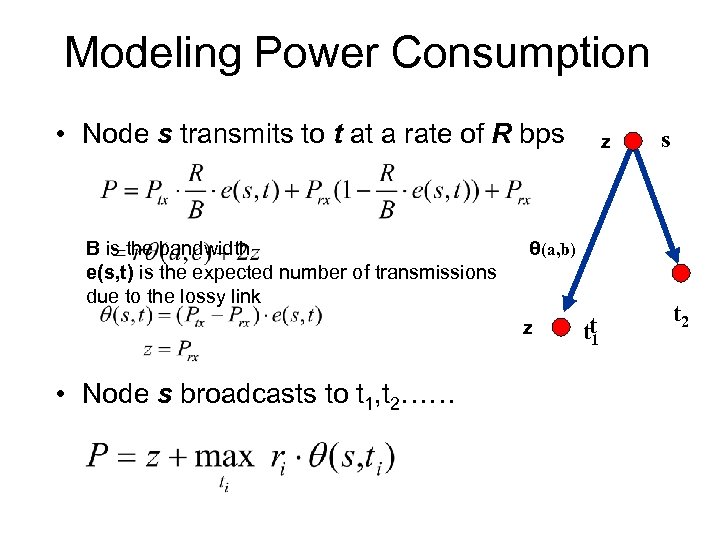
Modeling Power Consumption • Node s transmits to t at a rate of R bps B is the bandwidth e(s, t) is the expected number of transmissions due to the lossy link s θ(a, b) z • Node s broadcasts to t 1, t 2…… z tt 1 t 2

Min-power Multi-resolution Data Dissemination (MMDD) • Given traffic demands I={(ti , ri )} arriving online, find a tree T(V, E) minimizing |V | z node cost, independent of data rate + d(u): set of decedents of u c(u): set of children of u • Sleep scheduling + power-aware multicast • MMDD is NP-Hard

Lightweight Tree Adaptation • When data rates of existing requests change – Power efficiency of a tree degrades – Constructing a new tree is expensive • Path-quality based tree adaptation – Monitor the quality of each path – Find a new path if quality drops below a threshold • Reference-rate based tree adaptation – Monitor the reference of all data rates – Find a new tree if reference exceeds a threshold

Path Quality Estimation with Decreased Data Rate • Yl and Yh are best paths from s to t under rl and rh – Shortest paths under metric z + r θ(u, v) • Theorem I: If rh drops to rl, then power cost of Yh is no more than the min power under rl by: all symbols are known! • Significance: path quality degradation can be estimated solely by known information

Path Quality Estimation with increased Data Rate • Theorem II: If rl increases to rh, then power cost of Yl is no more than min power under rh by all symbols are known!

Path-quality based Tree Adaptation • Suppose sink t changes rate from r to r* • Computes ∆P, the difference between current power and the min power under r* • If ∆P×T > β, find a new path using r*, otherwise, continue to use the existing path – T is the duration of new rate r* – βis the energy cost of finding a shortest path

Reference-rate based Tree Adaptation • Find paths using same rate r for all sinks – Significantly reduces the overhead • Theorem: for D data requests with rates in [rmin, rmax], the performance ratio is D(rmax/rmin), if rmin ≤ rmax holds

Recent Projects • Rendezvous Planning in Mobility-assisted Wireless Sensor Networks, – 28 th IEEE Real-Time Systems Symposium (RTSS), 2007, acceptance ratio 44/171=25. 7% • Dynamic multi-resolution data dissemination – 10 th ACM/IEEE International Symposium on Modeling, Analysis and Simulation of Wireless and Mobile Systems (MSWi. M), 2007, acceptance ratio 41/161=24. 8% • Unified Radio Power Management Architecture – International Symposium on Information Processing in Sensor Networks (IPSN), 2007, acceptance ratio 38/170=22. 3%

Problem • Communication power cost is high Explosion in the development of various radio power management protocols • Protocols make different assumptions No single protocol is suited to the needs of every application • Existing radio stack architectures are monolithic Hard to develop new protocols or tune existing ones to specific application requirements

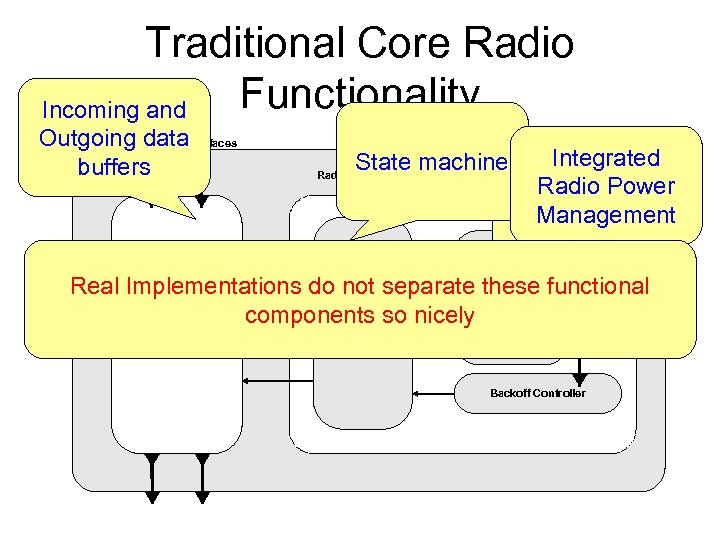
Traditional Core Radio Functionality Incoming and Outgoing data. Interfaces Send/Receive buffers Power Management Interfaces Backoff Control Interfaces Integrated Radio Power MAC Management CCA Radio Power Functionality Management State machine Radio Component Real Implementations do not separate these functional Radio State Send/Receive components so nicely. Clear Channel Machine Buffers Assessment Backoff Controller

Solution: UPMA • Unified Radio Power Management Architecture • Monolithic --> Composable radio stack architecture • Pluggable power management policies • Separation of power management features • Cross layer in nature

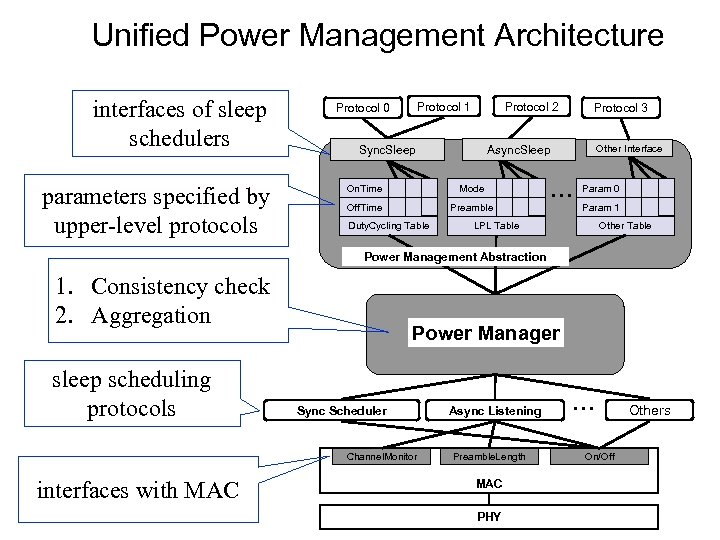
Unified Power Management Architecture interfaces of sleep schedulers parameters specified by upper-level protocols Protocol 1 Protocol 0 Protocol 2 … Sync. Sleep Other Interface Async. Sleep On. Time Mode Off. Time Preamble Duty. Cycling Table Protocol 3 … Param 0 Param 1 LPL Table Other Table Power Management Abstraction 1. Consistency check 2. Aggregation sleep scheduling protocols Power Manager Sync Scheduler Channel. Monitor interfaces with MAC Async Listening Preamble. Length MAC PHY … On/Off Others

Implementation • Implemented UPMA in Tiny. OS 2. 0 for both Mica 2 and Telosb motes • Developed interfaces with different types of MAC – CSMA based: S-MAC [Ye et al. 04], B-MAC [Polastre et al. 04] – TDMA based: TRAMA [Rajendran et al. 05] – Hybrid: 802. 15. 4, Z-MAC [Rhee et al. 05] • Separated sleep scheduling modules from B-MAC • Implemented two new sleep schedulers on top of B-MAC

Conclusions • Rendezvous based data collection – Combined In-network caching + controlled mobility – Developed rendezvous planning algorithms with/without data aggregation • Dynamic multi-resolution data dissemination – Modeled impact of data rate on power consumption – Proposed two dynamic tree adaptation algorithms • Unified radio power management architecture – Designed and implemented a link-layer power management architecture

References • Rendezvous Planning in Mobility-assisted Wireless Sensor Networks, Guoliang Xing, Tian Wang, Zhihui Xie and Weijia Jia, The 28 th IEEE Real-Time Systems Symposium (RTSS), acceptance ratio 44/171=25. 7% • Dynamic Multi-resolution Data Dissemination in Storage-centric Wireless Sensor Networks, Hongbo Luo, Guoliang Xing, Minming Li, Xiaohua Jia, 10 th ACM/IEEE International Symposium on Modeling, Analysis and Simulation of Wireless and Mobile Systems (MSWi. M), acceptance ratio 41/161=24. 8%. • Link Layer Support for Unified Radio Power Management in Wireless Sensor Networks, Kevin Klues, Guoliang Xing, Chenyang Lu, International Symposium on Information Processing in Sensor Networks (IPSN), acceptance ratio 38/170=22. 3%.