Ременные передачи 1 Ременные передачи l Ременная

Ременные передачи 1

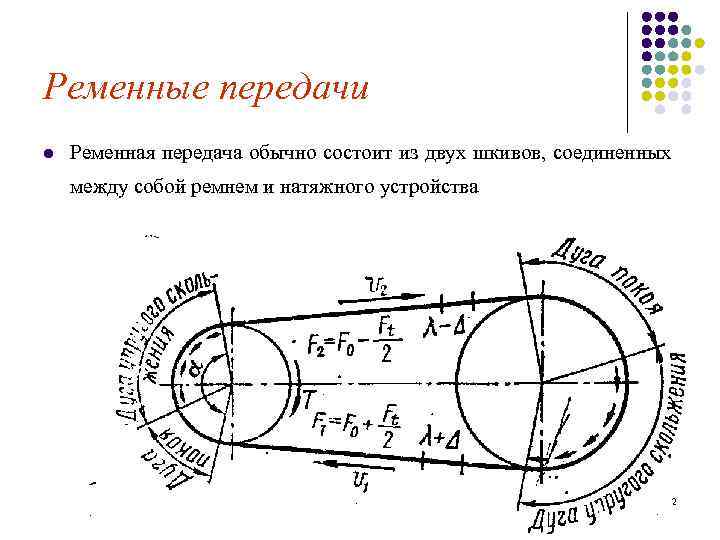Ременные передачи l Ременная передача обычно состоит из двух шкивов, соединенных между собой ремнем и натяжного устройства 2

Ременные передачи l l Обычно с помощью ремня передают движение между параллельными валами, однако благодаря закручиванию ремня реализуют передачи с вращением шкивов в противоположные стороны, а так же передачи с перекрещивающимися осями. По форме ремней различают плоско-, круглои клиноременные передачи. 3

Ременные передачи l Основное достоинство передач: простота конструкции, сравнительно малая стоимость, способность передавать вращательное движение на большие расстояния, работать с высокими скоростями, плавность работы и малый шум, малая чувствительность к толчкам, ударам и перегрузкам, отсутствие смазочной системы. 4

Ременные передачи l l Основные недостатки: невысокая долговечность ремня, большие радиальные габариты, значительные нагрузки на валы и опоры, непостоянство передаточного отношения. Ременную передачу применяют обычно как быстроходную ступень привода, устанавливая ведущий шкив на вал электродвигателя, в этом случае ее габариты и масса оказываются сравнительно небольшими. 5

Ременные передачи l Движение ремня по шкиву сопровождается упругим скольжением. Такой характер движения впервые исследован профессором И. Е. Жуковским и определяет основные особенности работы передачи. 6

Ременные передачи l Полезная нагрузка Ft передачи, развивается в основном за счет сил трения по дуге скольжения: 7

Ременные передачи l При вращении ведущего шкива в угловой скоростью 1 его окружная скорость 8

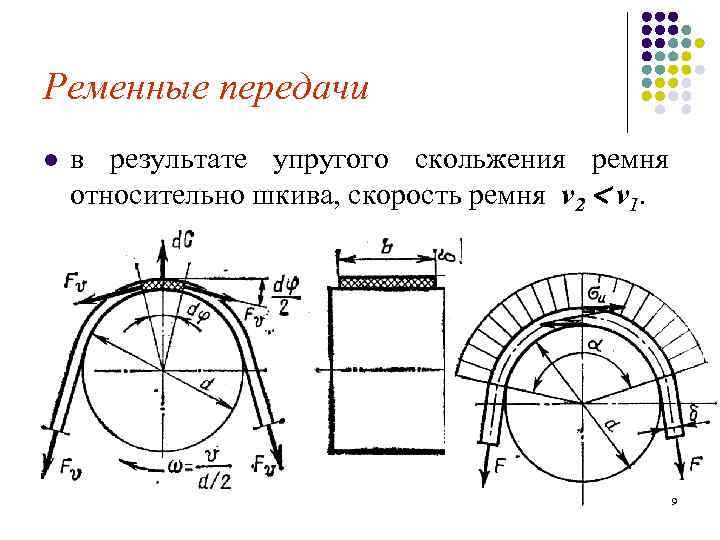Ременные передачи l в результате упругого скольжения ремня относительно шкива, скорость ремня v 2 v 1. 9

Ременные передачи l Коэффициент упругого определяется по формуле: скольжения l где — угловая скорость и диаметр ведомого шкива. 10

Ременные передачи l Передаточное отношение передачи: 11

Ременные передачи l l l В расчетах, на основании экспериментов, принимают: = 0, 01 — для плоскоременных передач, = 0, 015. . . 0, 020 — для клиноременных передач. 12

Ременные передачи l Силы в передаче. l Ременные передачи фрикционные, поэтому начальное натяжение ремня — необходимое условие ее работы. Связь между силами F 1 и F 2 обычно устанавливается по формуле Эйлера, когда скорость ремня не превышает 10 м/с: l 13

Ременные передачи l l l Силу начального натяжения ветвей передачи приближенно связать с силами в ветвях ремня: F 1 = F 0 +0, 5 Ft; F 2 = F 0 +0, 5 Ft; =0, 5(F 1+ F 2); F 0 можно тогда F 0 отсюда следует, что сила предварительного натяжения определяется внешней нагрузкой и геометрией ремня. 14

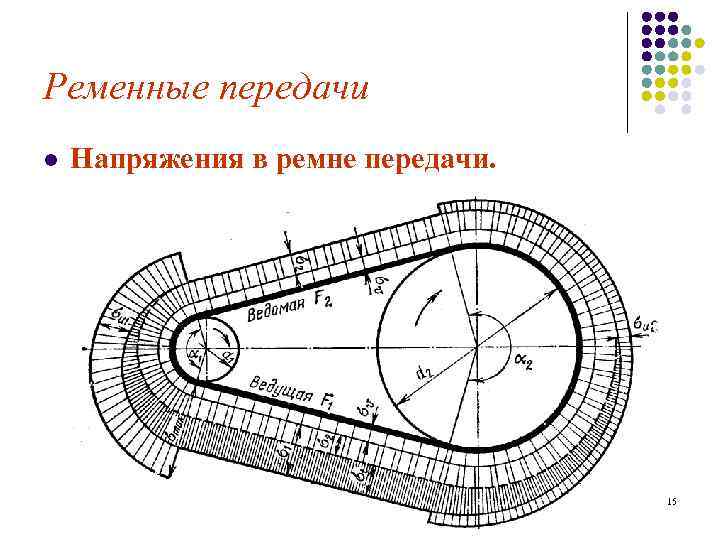Ременные передачи l Напряжения в ремне передачи. 15

Ременные передачи l l Напряжения от начального натяжения: принимают 0 = 1, 2. . . 1, 8 МПа — для прорезиненных ремней, 0 = 50 МПа — для капроновых ремней, А — площадь поперечного сечения ремня. 16

Ременные передачи l Напряжение от действия центробежных сил: ц = 10 -3 l 2 v где = 1, 2. . . 1, 25 Г/см 3 — плотность ремня. 17

Ременные передачи l Напряжения от изгиба ремня : l где h — толщина ремня, E — приведенный модуль упругости: E = 200. . . 300 МПа — для прорезиненных ремней, E = 600 МПа — для капроновых ремней. E = 500. . . 600 МПа — для клиновых кордотканевых ремней. l l l 18

Ременные передачи l l Для ремней критическая окружная скорость на шкиве определяют по формуле при которой ц = 0 передача не может передавать движение. Найвыгоднейшая скорость для ременных передач 20. . . 25 м/с, а наибольшая допустимая 30. . . 35 м/c. 19

Ременные передачи l l Тяговая способность ременной передачи. Фактическую тяговую способность передачи характеризует окружная сила Ft или вращающийся момент T. 20

Ременные передачи l где — коэффициент тяги. l Для получения высокой тяговой способности передач рекомендуется обеспечивать 150 для плоскоременной передачи и 120 — для клиноременной передачи. 21

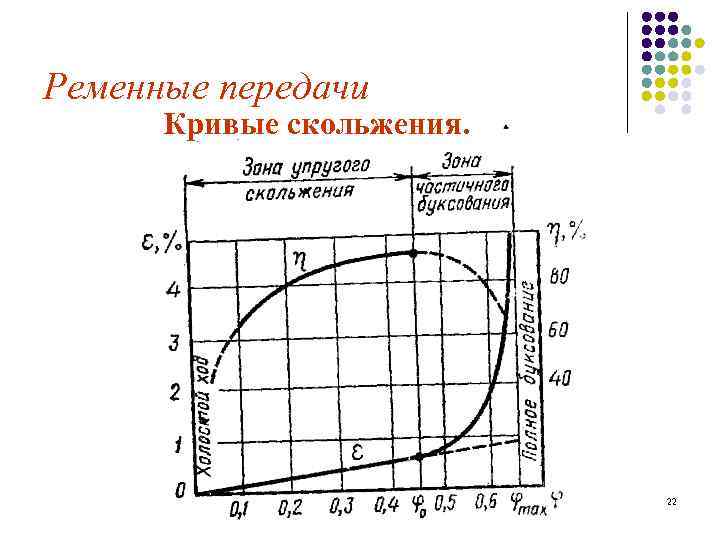Ременные передачи Кривые скольжения. 22

Ременные передачи l Работоспособность ременной передачи принято характеризовать кривыми скольжения и к. п. д. (рис. ) Такие кривые являются результатом испытаний ремней различных типов и материалов. На графике по оси ординат отсчитывают относительное скольжение и к. п. д. , а по оси абсцисс — нагрузку передачи, которую выражают через коэффициент тяги 23

Ременные передачи l Коэффициент тяги позволяет судить о том, какая часть предварительного натяжения ремня F 0 используется полезно для передачи нагрузки Ft , т. е. характеризует степень загруженности передачи. Целесообразность выражения нагрузки передачи через безразмерный коэффициент объясняется тем, что скольжение и к. п. д. связаны именно со степенью загруженности передачи, а не с абсолютным значением нагрузки. 24

Ременные передачи l На начальном участке кривой скольжения от 0 до 0 наблюдается только упругое скольжение. Так как упругие деформации ремня приближенно подчиняются закону Гука, этот участок близок к прямолинейному. Дальнейшее увеличение нагрузки приводит к частичному, а затем и полному буксованию. В зоне 0. . max наблюдается как упругое скольжение, так и буксование. Они разделяются продолжением прямой в штриховой линией. 25

Ременные передачи l Рабочую нагрузку рекомендуют выбирать вблизи критического значения 0 и слева от нее. Этому значению соответствует также и максимальное значение к. п. д. Работу в зоне частичного буксования допускают только при кратковременных перегрузках, например при пуске. В этой зоне к. п. д. резко снижается вследствие увеличения потерь на скольжение ремня, а ремень быстро изнашивается. 26

Ременные передачи l l l Размер зоны частичного буксования характеризует способность передачи воспринимать кратковременные перегрузки. Отношение max / 0 для ремней: плоских кожаных и шерстяных 1, 35. . . 1, 5 прорезиненных 1, 15. . . 1, 3 хлопчатобумажных 1, 25. . . 1, 4 клиновых 1, 5. . . l, 6 27

Ременные передачи l КПД ременных передач. Коэффициент полезного действия ременных передач обычно определяют по формуле: l зависит от коэффициента тяги, обычно оптимальное КПД при = 0, 4. . . 0, 5 — для плоскоременных передач, = 0, 6. . . 0, 7 — для клиноременных передач. 28

Ременные передачи l l l Критерии работоспособности ременных передач. Опыт эксплуатации ременных передач показал, что их работоспособность ограничена тяговой способностью и долговечностью ремня. В первом случае ремень теряет тяговую способность из-за буксования в связи с недостаточной прочностью сцепления ремня со шкивами (ведущий шкив вращается, а ведомый остается неподвижным). В результате буксования ремень нагревается и выходит из строя. Поэтому в отличие от упругого скольжения буксование в ременной передаче недопустимо. Во втором случае выход из строя ремня связан с усталостным разрушением. 29

Ременные передачи l Расчет ременной передачи на тяговую способность основан на показателях тяговой способности и долговечности. Для расчета используют условие работоспособности передачи в форме: l l где t — удельная окружная сила, называемая полезным напряжением, А — площадь поперечного сечения ремня (комплекта ремней). 30

Ременные передачи l Расчет клиноременной передачи сводится к определению требуемого числа ремней по формуле: l где А — площадь сечения одного ремня, Сz — коэффициент неравномерности распределения нагрузки между ремнями в комплекте: 31

Ременные передачи 32

Ременные передачи l Для поликлиновых ремней определяют число ребер ремня по формуле: l где А 10 — площадь сечения ремня с 10 -ми ребрами. 33

Ременные передачи l На практике расчет клиноременной передачи часто выполняют по передаваемой мощности и требуемому числу ремней: l где Р — передаваемая передачей мощность, [P] — допускаемая мощность на один ремень. l 34

Ременные передачи l Для плоскоременной передачи расчет сводится к определению ширины ремня по формуле: l где Ср — коэффициент динамичности учитывает режим работы (табулирован в справочной литературе), h — толщина ремня, [ t] — допускаемое напряжение. 35

Ременные передачи l Допускаемые напряжения в ремне находят из условия прочностной надежности 1 max E — максимальное эффективное напряжение, которое ремень выдерживает NE циклов. На основании экспериментальных исследований кривых усталости ремней определяется так называемая С— константа для каждого типа ремня. С = 60. . . 70 МПа — для плоских прорезиненных ремней, С = 90. . . 100 МПа — для клиновых ремней. l l 36

Ременные передачи l Вводится понятие — число пробегов ремня: l где v — скорость ремня, м/с; l — длина ремня, м. 37

Ременные передачи l Подсчитывается эффективное число циклов за весь срок службы по формуле: l где zш — число шкивов в передаче. 38

Ременные передачи l Определяют максимальное общее напряжение в ремне по формуле: l где m — показатель степени кривой усталости ремня. m = 5. . . 6 — для прорезиненных ремней m = 7. . . 11 — для клиновых ремней l 39

Ременные передачи l или : l эта зависимость связывает тяговую способность, характеризуемую параметром q или полезной нагрузкой t с долговечностью ремня. 40

Ременные передачи l Ременную передачу можно рассчитать и по другим упрощенным методикам, которые учитывают опыт эксплуатации ременных передач. Есть отдельные методики расчета каждого типа ремня ременной передачи, которые также можно использовать в курсовом проектировании. 41

Ременные передачи l l l Геометрические параметры ременной передачи. Для ограничения напряжения изгиба и минимальное значение диаметра меньшего шкива dmin регламентировано стандартом для каждого типа ремня (см. справочную литературу). Для клиновых ремней d 1 1, 2 dmin. 42

Ременные передачи l У передач с плоским ремнем для меньшего шкива рекомендуют 70 при v = 50. . . 100 м/с. l Минимальное межосевое расстояние: l в плоскоременных передачах аmin= 2)(d 1+d 2); . l (1, 5 . . . в клиноременной (на основании практики) аmin= 0, 55(d 1+d 2)+h; 43

Ременные передачи l Максимальное amax по экономическим соображениям (увеличение габаритов и стоимости ремней) и для предотвращения поперечных колебаний ограничивают: amax= (1, 5. . . 2)(d 1+d 2); 44

Ременные передачи l Требуемая длина ремня при заданными межосевым расстоянии а и угле обхвата : 45

Ременные передачи l угол обхвата меньшего шкива: l Конструкции ремней и шкивов (самостоятельно по справочной литературе) 46