Relativistic Outflow Formation by Magnetic Field around Rapidly

Relativistic Outflow Formation by Magnetic Field around Rapidly Rotating Black Hole Shinji Koide　（Toyama University） General relativistic magnetohydrodynamic (MHD) simulation shows relativistic outflow is driven around rapidly rotating black hole by radial magnetic field. This is the first self-consistent solution of spontaneous relativistic outflow formation in black hole magnetosphere. Black Hole 2003, October 29 (Wed), 2003 @ Kyoto International Community House

Relativistic Jets in the Universe 1) Active galactic nuclei, Quasars: γ>10 ~ 2) Microquasars: γ~ 3 3) Gamma-ray bursts: γ>~100 Relativistic Jet Formation Mechanism by Magnetic Field Acceleration of plasma/gas Collimation of plasma/gas outflow

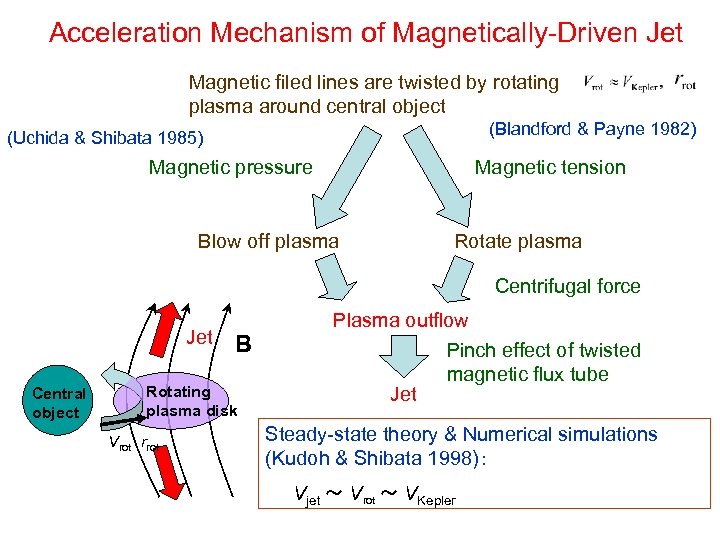
Acceleration Mechanism of Magnetically-Driven Jet Magnetic filed lines are twisted by rotating plasma around central object (Blandford & Payne 1982) (Uchida & Shibata 1985) Magnetic pressure Magnetic tension Blow off plasma Rotate plasma Centrifugal force Jet Central object B Rotating plasma disk Vrot rrot Plasma outflow Pinch effect of twisted magnetic flux tube Jet Steady-state theory & Numerical simulations (Kudoh & Shibata 1998)： Vjet ～ Vrot ～ VKepler

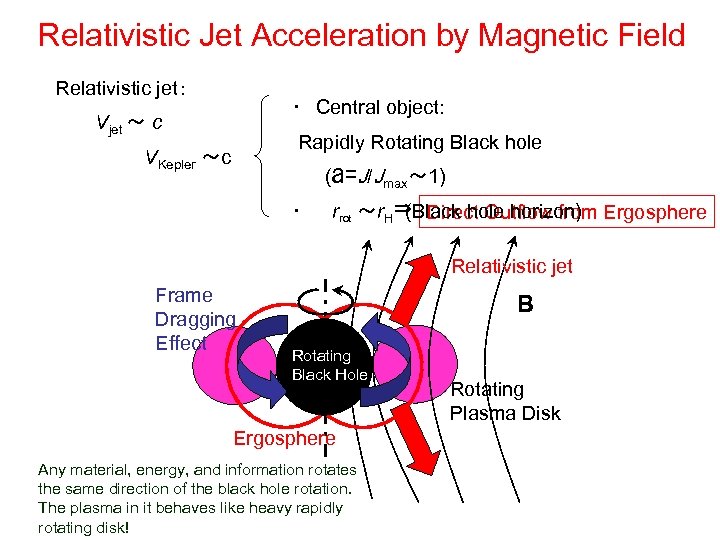
Relativistic Jet Acceleration by Magnetic Field Relativistic jet：・　Central object: 　　　Vjet ～ c Rapidly Rotating Black hole VKepler ～c 　　(a=J/Jmax～ 1) ⇒ Direct Outflow from ・　 rrot ～r. H　(Black hole horizon) Ergosphere Relativistic jet Frame Dragging Effect B Rotating Black Hole Ergosphere Any material, energy, and information rotates the same direction of the black hole rotation. The plasma in it behaves like heavy rapidly rotating disk! Rotating Plasma Disk

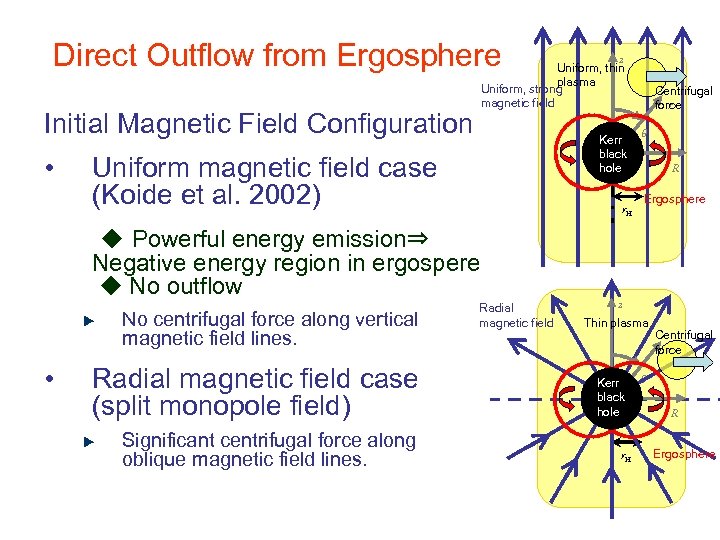
Direct Outflow from Ergosphere z Uniform, thin plasma Uniform, strong magnetic field Initial Magnetic Field Configuration • Kerr black hole Uniform magnetic field case (Koide et al. 2002) r. H ◆ Powerful energy emission⇒ Negative energy region in ergospere ◆ No outflow No centrifugal force along vertical magnetic field lines. • Radial magnetic field case (split monopole field) Significant centrifugal force along oblique magnetic field lines. Radial magnetic field Centrifugal r force q R Ergosphere z Thin plasma Kerr black hole r. H Centrifugal force r q R Ergosphere

Initial Condition: Simple system of rotating black hole, thin plasma, and radial magnetic field • Black Hole: 　　　　　 (nearly maximally rotating black hole) • Magnetic Field： Radial magnetic field , B 0=B(R=r. S, z=0) • Plasma：　Magnetic field dominates: ρ0=0. 018 B 02/c 2 Gas falling near the horizon. Hydrostatic equilibrium far from black hole. , , ,

General Relativistic MHD Equations in Kerr Space-Time • General relativistic equation of conservation laws and Maxwell equations: 　　　　　　　　　　∇n ( n U n ) = 0　　　　　　　　　　∇n T mn = 0 (conservation of particle number) (conservation of energy and momentum) (Maxwell equations) 　　　　　　　∂m. Fnl + ∂ n. Flm + ∂ l. F mn = 0 　　　　　　　∇m. F mn = - J n Fnm. Un = 0 • Frozen-in condition: • Kerr Metric：　ds = gmn dx dx ; 2 g 00 = - h 02 ; 　　　 m n gii = - hi 2 ; g 0 i = - hi 2 wi (i=1, 2, 3) ; gij = 0 (i≠j) n: proper particle number density. p : proper pressure. c: speed of light. e : proper total energy density, e=mnc 2 + p / (G -1). m : rest mass of particles. G: specific heat ratio. Umu : velocity four vector. Amu : potential four vector. Jmu : current density four vector. ∇mn : covariant derivative. gmn : metric. Tmn : energy momentum tensor, Tmn = pgmn + (e+p)Um Un+Fms. Fns -gmn. Flk/4. Fmn : field-strength tensor, Fmn =∂m An -∂n Am.

Vector Form of General Relativistic MHD Equation (3+1 Formalism)　 Special relativistic mass density, gr general relativistic effect (conservation of particle number) Special relativistic total momentum density (equation of motion) Special relativistic total energy density special relativistic effect (equation of energy) (Maxwell equations) (ideal MHD condition) where : (Lapse function) : (shift vector) : (shift velocity)

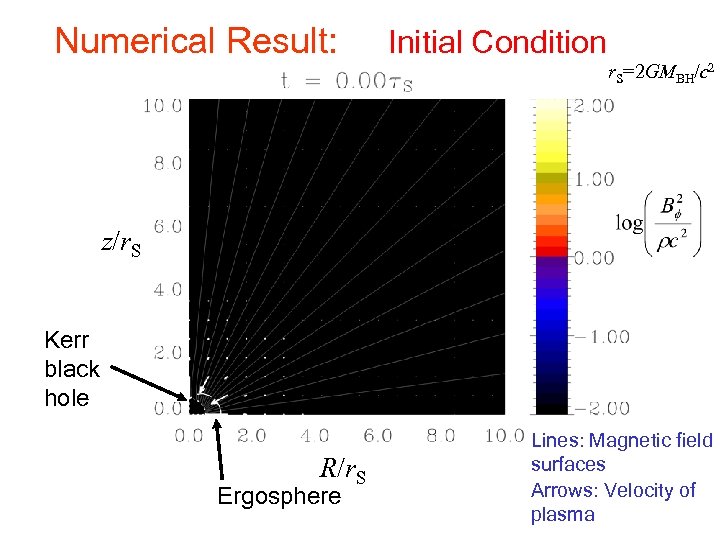
Numerical Result: Initial Condition r. S=2 GMBH/c 2 z/r. S Kerr black hole c R/r. S Ergosphere Lines: Magnetic field surfaces Arrows: Velocity of plasma

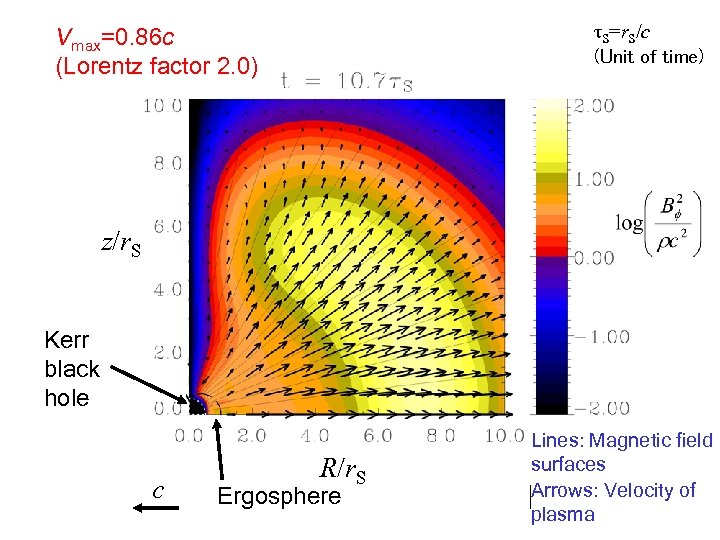
τS=r. S/c (Unit of time) Vmax=0. 86 c (Lorentz factor 2. 0) z/r. S Kerr black hole c R/r. S Ergosphere Lines: Magnetic field surfaces Arrows: Velocity of plasma

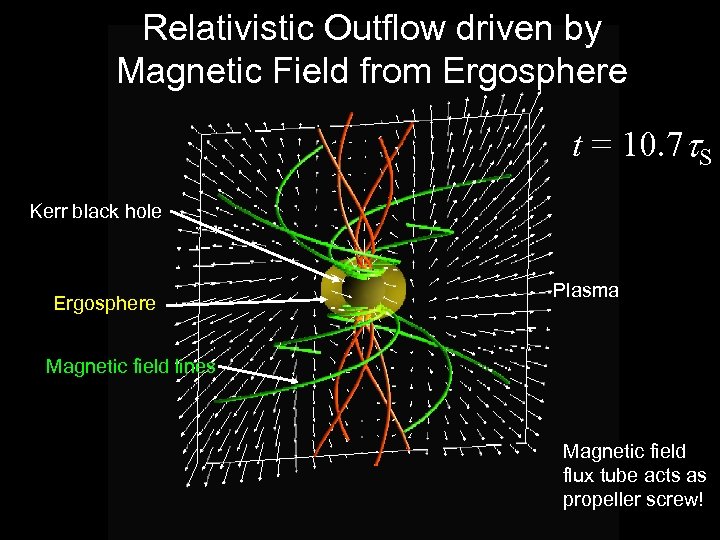
Relativistic Outflow driven by Magnetic Field from Ergosphere t = 10. 7 t. S Kerr black hole Ergosphere Plasma Magnetic field lines Magnetic field flux tube acts as propeller screw!

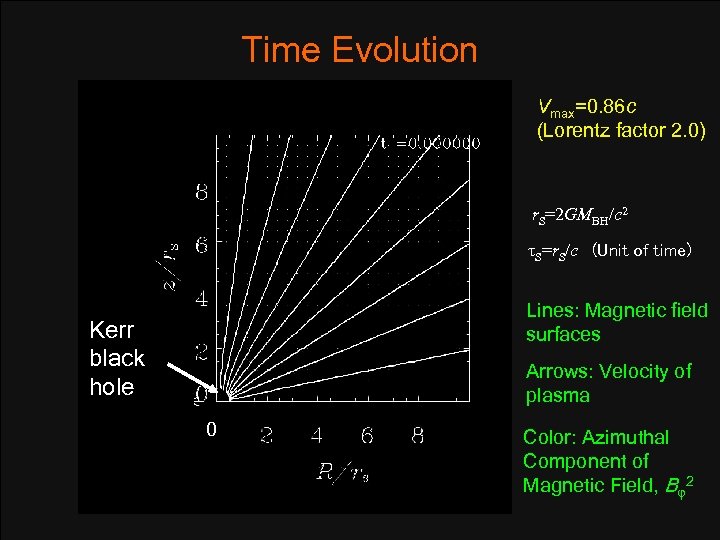
Time Evolution Vmax=0. 86 c (Lorentz factor 2. 0) r. S=2 GMBH/c 2 τS=r. S/c (Unit of time) Lines: Magnetic field surfaces Kerr black hole Arrows: Velocity of plasma 0 Color: Azimuthal Component of Magnetic Field, Bφ2

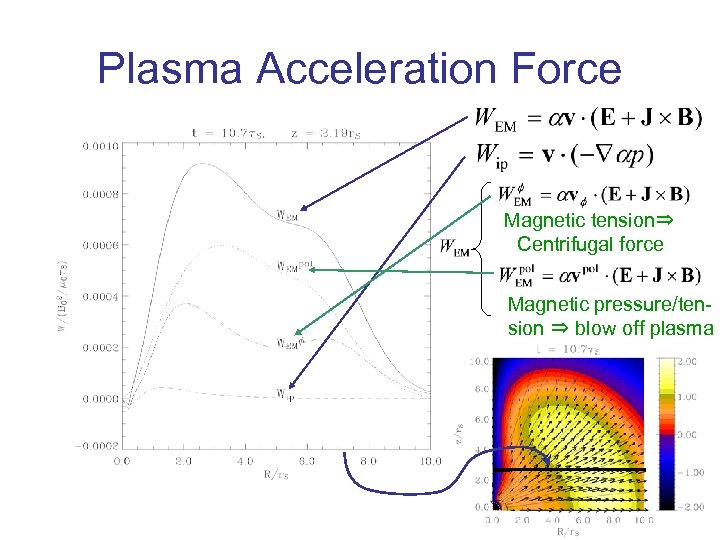
Plasma Acceleration Force Magnetic tension⇒ 　Centrifugal force Magnetic pressure/tension ⇒ blow off plasma

Summary General Relativistic MHD simulation shows that magnetic field configuration dominates relativistic outflow formation near rapidly rotating black hole ( ). □ Uniform magnetic field case (Koide et al. 2002): Powerful magnetic energy emission. No outflow. ■ Radial magnetic field case (present result): Relativistic plasma outflow from ergosphere. Lorentz factor, 2. 0 (Vmax=0. 86 c). • The plasma is accelerated by magnetic force (Lorentz force). Contribution of magnetic pressure/tension (⇒ blow off plasma) and magnetic tension (⇒ centrifugal force) are almost comparable. • The outflow is not pinched by magnetic field significantly and no collimated jet is found. After the long term simulation, it is expected that the magnetic tension of the twisted magnetic flux tube pinches the outflow to form a relativistic jet.

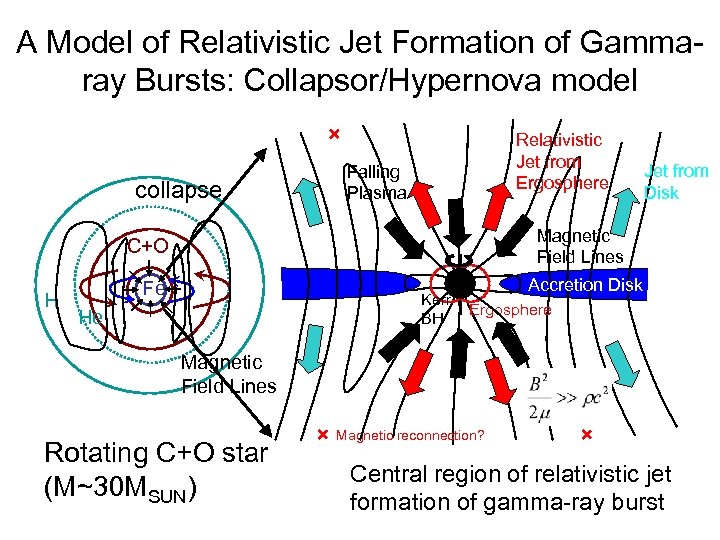
A Model of Relativistic Jet Formation of Gammaray Bursts: Collapsor/Hypernova model collapse Relativistic Jet from Ergosphere Falling Plasma Magnetic Field Lines C+O H Jet from Disk Fe Kerr BH He Accretion Disk Ergosphere Magnetic Field Lines Rotating C+O star (M~30 MSUN) Magnetic reconnection? Central region of relativistic jet formation of gamma-ray burst