Relational String Verification Using Multitrack Automata Fang Yu

Relational String Verification Using Multitrack Automata Fang Yu, Tevfik Bultan, and Oscar Ibarra Department of Computer Science University of California, Santa Barbara

Web software • Web software is becoming increasingly dominant • Web applications are used extensively in many areas: – Commerce: online banking, online shopping, … – Entertainment: online music & videos, … – Interaction: social networks • We will rely on web applications more in the future: – Health records • Google Health, Microsoft Health. Vault – Controlling and monitoring of national infrastructures: • Google Powermeter • Web software is also rapidly replacing desktop applications – Could computing + software-as-service • Google Docs, Google …

One Major Road Block • Web applications are not secure! • Web applications are notorious for security vulnerabilities – Their global accessibility makes them a target for many malicious users • As web applications are becoming increasingly dominant and as their use in safety critical areas is increasing – Their security is becoming a critical issue

Web applications are not secure • There are many well-known security vulnerabilities that exist in many web applications. Here are some examples: – Malicious file execution: where a malicious user causes the server to execute malicious code – SQL injection: where a malicious user executes SQL commands on the back-end database by providing specially formatted input – Cross site scripting (XSS): causes the attacker to execute a malicious script at a user’s browser • These vulnerabilities are typically due to – errors in user input validation or – lack of user input validation

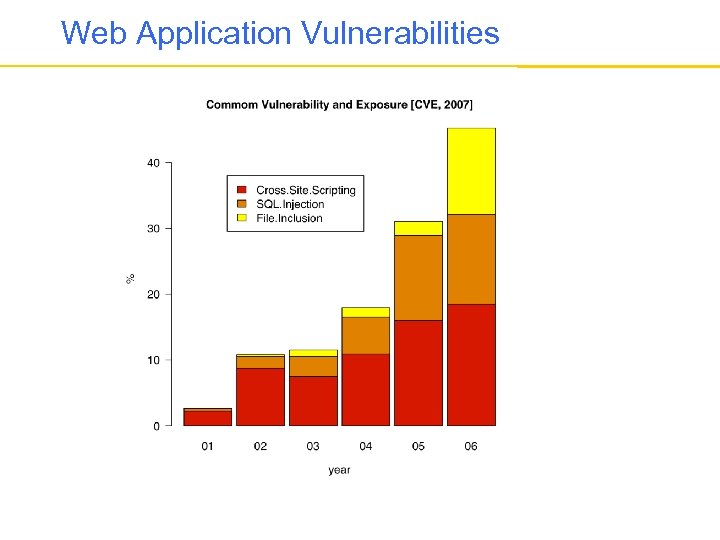Web Application Vulnerabilities

Web Application Vulnerabilities • The top two vulnerabilities of the Open Web Application Security Project (OWASP)’s top ten list in 2007 – Cross Site Scripting (XSS) – Injection Flaws (such as SQL Injection) • The top two vulnerabilities of the OWASPs top ten list in 2010 – Injection Flaws (such as SQL Injection) – Cross Site Scripting (XSS)

Why are web applications error prone? • Extensive string manipulation: – Web applications use extensive string manipulation • To construct html pages, to construct database queries in SQL, etc. – The user input comes in string form and must be validated and sanitized before it can be used • This requires the use of complex string manipulation functions such as string-replace – String manipulation is error prone

String Related Vulnerabilities String related web application vulnerabilities occur when: a sensitive function is passed a malicious string input from the user This input contains an attack User input is not properly sanitized before it reaches the sensitive function String analysis: Discover these vulnerabilities automatically

XSS Vulnerability A PHP Example: 1: ”. $l_otherinfo. ”: ”. $www. ””; 5: ? > The echo statement in line 4 is a sensitive function It contains a Cross Site Scripting (XSS) vulnerability

String Analysis String analysis determines all possible values that a string expression can take during any program execution Using string analysis we can identify all possible input values of the sensitive functions Then we can check if inputs of sensitive functions can contain attack strings How can we characterize attack strings? Use regular expressions to specify the attack patterns Attack pattern for XSS: Σ∗

String Systems stmt : : = id : = sexp; | id : = call id (sexp); if exp then goto l; | (where l is a stmt label) goto L; | (where L is a set of stmt labels) input id; | output exp; | assert exp; exp : : = bexp | exp and exp | not exp bexp : : = atom = sexp : : = sexp. atom | suffix(id) | prefix(id) atom : : = id | c (where c is a string constant)

Basic String System Categorization We use the following categorization • N/D: nondeterministic or deterministic • U/B/K: unary, binary or arbitrary alphabet • The set of variables • The types of statements • The types of branch conditions Example: NB(X 1, X 2) Xi : = Xi. c; X 1 = X 2 Nondeterministic, binary alphabet, variables X 1, X 2, statements of the form Xi : = Xi. c, branch conditions of the form X 1 = X 2 Define the reachability problem for the string systems as: Given a string system and a configuration (an instruction label and values for the variables) is that configuration reachable?

Decidability Results Reachability problem for: • NB(X 1, X 2) Xi : = Xi. c; X 1 = X 2 is undecidable – Reduction from Post Correspondence Problem • DU(X 1, X 2, X 3) Xi : = Xi. c; X 1 = X 3, X 2 = X 3 is undecidable – Can simulate 2 -counter machines • NK(X 1, . . . , Xk) Xi : = d. Xi. c; c = Xi, c = prefix(Xi), c=suffix(Xi) is decidable – Reduction to emptiness check for multi-tape automaton • DK(X 1, . . . , Xk) Xi : = Xi. a, Xi : = a. Xi; X 1 = X 2, c = Xi, c = prefix(Xi), c = suffix(Xi) is decidable. – Can bound the execution steps if there is no infinite loop

Automata-based String Analysis • Finite State Automata can be used to characterize sets of string values • We use automata based string analysis – Associate each string expression in the program with an automaton – The automaton accepts an over approximation of all possible values that the string expression can take during program execution • Using this automata representation we symbolically execute the program, only paying attention to string manipulation operations

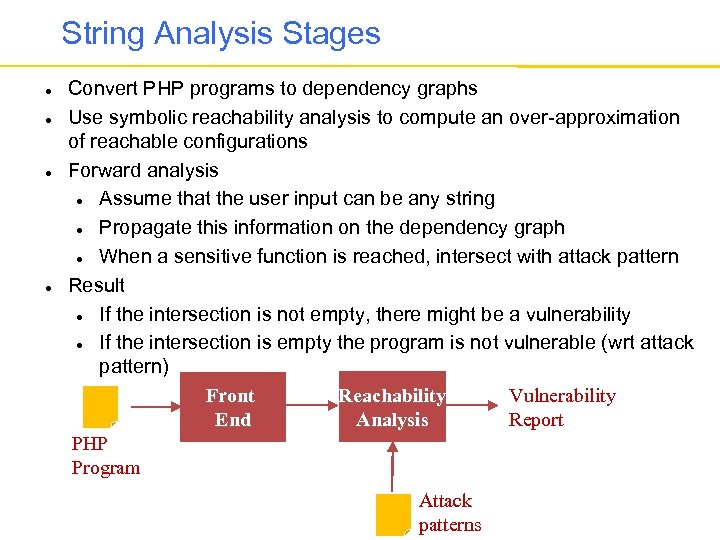String Analysis Stages Convert PHP programs to dependency graphs Use symbolic reachability analysis to compute an over-approximation of reachable configurations Forward analysis Assume that the user input can be any string Propagate this information on the dependency graph When a sensitive function is reached, intersect with attack pattern Result If the intersection is not empty, there might be a vulnerability If the intersection is empty the program is not vulnerable (wrt attack pattern) Vulnerability Reachability Front Report Analysis End PHP Program Attack patterns

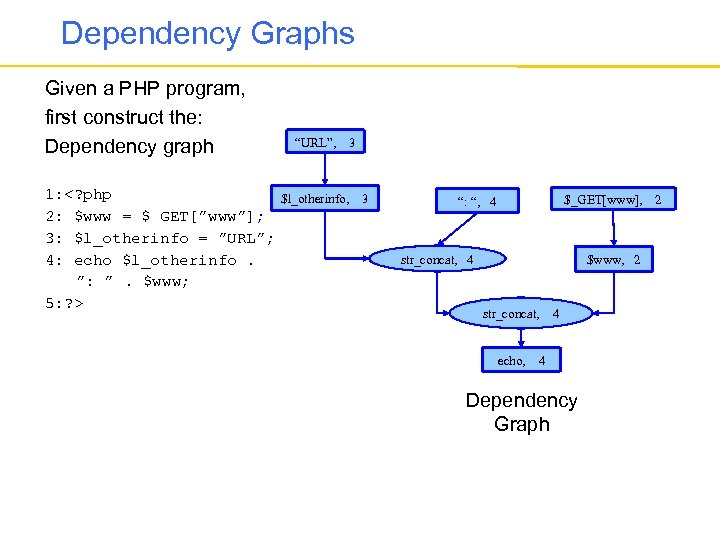Dependency Graphs Given a PHP program, first construct the: Dependency graph “URL”, 3 1: $_GET[www], “: “, 4 str_concat, 4 $www, 2 str_concat, echo, 4 4 Dependency Graph 2

Symbolic Reachability Analysis • Using the dependency graph we conduct symbolic reachability analysis • Automata-based forward fixpoint computation that identifies the possible string values of each node – Each node in the dependency graph is associated with a DFA • DFA accepts an over-approximation of the strings values that the string expression represented by that node can take at runtime • The DFAs for the input nodes accept Σ∗ – Intersecting the DFA for the sink nodes with the DFA for the attack pattern identifies the vulnerabilities

Forward Analysis Attack Pattern = Σ*<Σ* Forward = Σ* “URL”, 3 $_GET[www], URL $l_otherinfo, “: “, 4 3 $www, 2 : Σ* URL str_concat, 4 URL: Σ* echo, 4 URL: Σ* L(Σ*<Σ*) ∩ L(URL: Σ*) = L(URL: Σ*< Σ*) ≠Ø 2

Relational String Analysis • Earlier work on string analysis use multiple single-track DFAs during symbolic reachability analysis – One DFA per variable per program location • Our approach: Use one multi-track DFA per program location – Each track represents the values of one string variable • Using multi-track DFAs: – Identifies the relations among string variables – Improves the precision of the path-sensitive analysis – Can be used to prove properties that depend on relations among string variables, e. g. , $file = $usr. txt

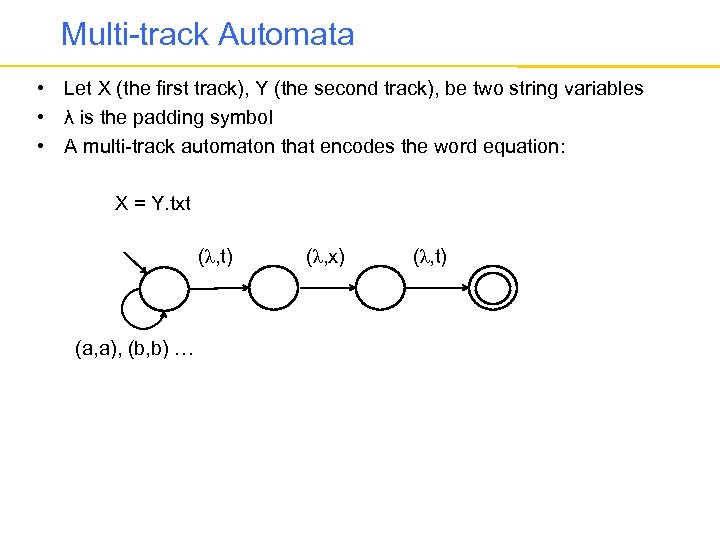Multi-track Automata • Let X (the first track), Y (the second track), be two string variables • λ is the padding symbol • A multi-track automaton that encodes the word equation: X = Y. txt (λ, t) (a, a), (b, b) … (λ, x) (λ, t)

Alignment • To conduct relational string analysis, we need to compute ”intersection” of multi-track automata – Intersection is closed under aligned multi-track automata • In an aligned multi-track automaton λs are right justified in all tracks, e. g. , abλλ instead of aλbλ • However, there exist unaligned multi-track automata that are not equivalent to any aligned multi-track automata – We propose an alignment algorithm that constructs aligned automata which over or under approximates unaligned ones • Over approximation: Generates an aligned multi-track automaton that accepts a super set of the language recognized by the unaligned multi-track automaton • Under approximation: Generates an aligned multi-track automaton that accepts a subset of the language recognized by the unaligned multi-track automaton

Symbolic Reachability Analysis • Transitions and configurations of a string system can be represented using word equations • Word equations can be represented/approximated using aligned multitrack automata which are closed under intersection, union, complement and projection • Operations required for reachability analysis (such as equivalence checking) can be computed on DFAs

Word Equations • Word equations: Equality of two expressions that consist of concatenation of a set of variables and constants – Example: X = Y. txt • Word equations and their combinations (using Boolean connectives) can be expressed using only equations of the form X = Y. c, X = c. Y, c = X. Y, X = Y. Z, Boolean connectives and existential quantification • Our goal: – Construct multi-track automata from basic word equations • The automata should accept tuples of strings that satisfy the equation – Boolean connectives can be handled using intersection, union and complement – Existential quantification can be handled using projection

Word Equations to Automata • Basic equations X = Y. c, X = c. Y, c = X. Y and their Boolean combinations can be represented precisely using multi-track automata • The size of the aligned multi-track automaton for X = c. Y is exponential in the length of c • The nonlinear equation X = Y. Z cannot be represented precisely using an aligned multi-track automaton

Word Equations to Automata • When we cannot represent an equation precisely, we can generate an over or under-approximation of it – Over-approximation: The automaton accepts all string tuples that satisfy the equation and possibly more – Under-approximation: The automaton accepts only the string tuples that satify the equation but possibly not all of them • We implement a function CONSTRUCT(equation, sign) – Which takes a word equation and a sign and creates a multi-track automata that over or under-approximation of the equation based on the input sign

Post condition computation • During symbolic reachability analysis we compute the post-conditions of statements using the function CONSTRUCT Given a multi-track automata M and an assignment statement: X : = sexp Post(M, X : = sexp) denotes the post-condition of X : = sexp with respect to M Post(M, X : = sexp) = ( X , M ∩ CONSTRUCT(X’ = sexp, +))[X/X’] • We implement a symbolic forward reachability computation using the post-condition operations – It is a least fixpoint computation – We use widening to achieve convergence

Widening • String verification problem is undecidable • The forward fixpoint computation is not guaranteed to converge in the presence of loops and recursion • We compute a sound approximation – During fixpoint we compute an over approximation of the least fixpoint that corresponds to the reachable states • We use an automata based widening operation to over-approximate the fixpoint – Widening operation over-approximates the union operations and accelerates the convergence of the fixpoint computation

Summarization • We developed techniques for handling function calls using summarization • We generate a transducer that is the summary of a function – It represents a relation between the arguments of the function and the value it returns – We generate a multi-track automaton for the function summary – We generate the function summary also using forward fixpoint computation and widening • We use the function summaries during reachability analysis to handle function calls

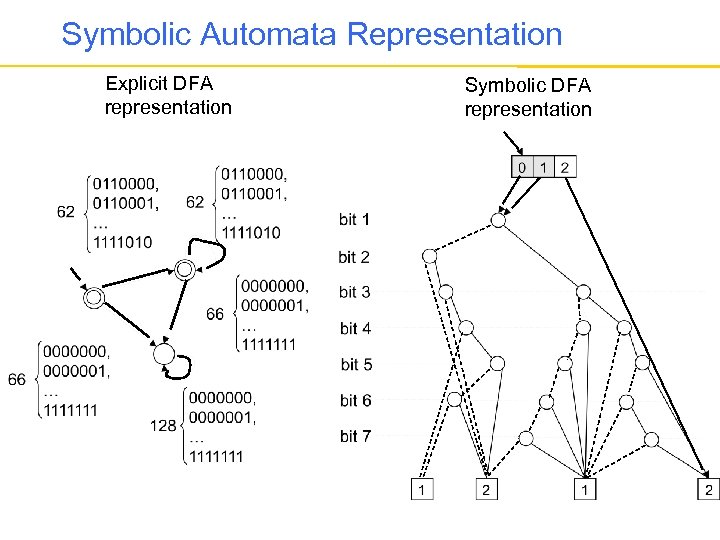
Symbolic Automata Representation • We used the MONA DFA Package for automata manipulation – [Klarlund and Møller, 2001] • Compact Representation: – The transition relation of the DFA is represented as a multi-terminal BDD (MBDD) • Exploits the MBDD structure in the implementation of DFA operations – Union, Intersection, and Emptiness Checking – Projection and Minimization • Cannot Handle Nondeterminism: – We extended the alphabet with dummy bits to encode nondeterminism

Symbolic Automata Representation Explicit DFA representation Symbolic DFA representation

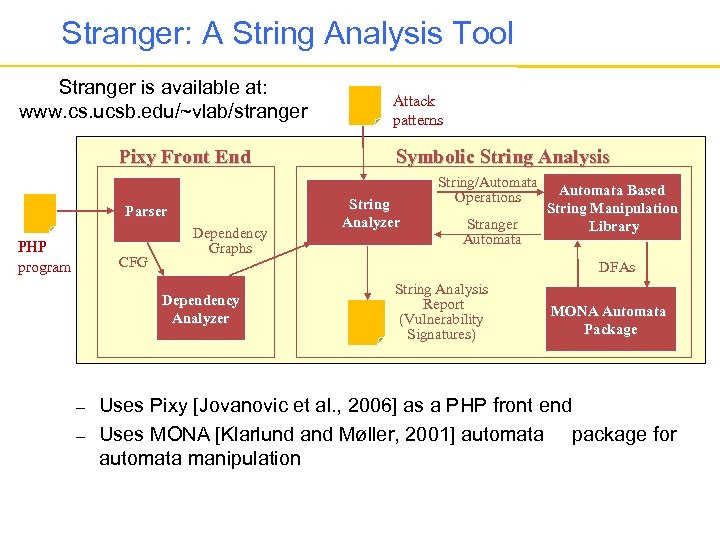Stranger: A String Analysis Tool Stranger is available at: www. cs. ucsb. edu/~vlab/stranger Pixy Front End Parser PHP program CFG Dependency Graphs – Symbolic String Analysis String Analyzer String/Automata Operations Stranger Automata Based String Manipulation Library DFAs Dependency Analyzer – Attack patterns String Analysis Report (Vulnerability Signatures) MONA Automata Package Uses Pixy [Jovanovic et al. , 2006] as a PHP front end Uses MONA [Klarlund and Møller, 2001] automata package for automata manipulation

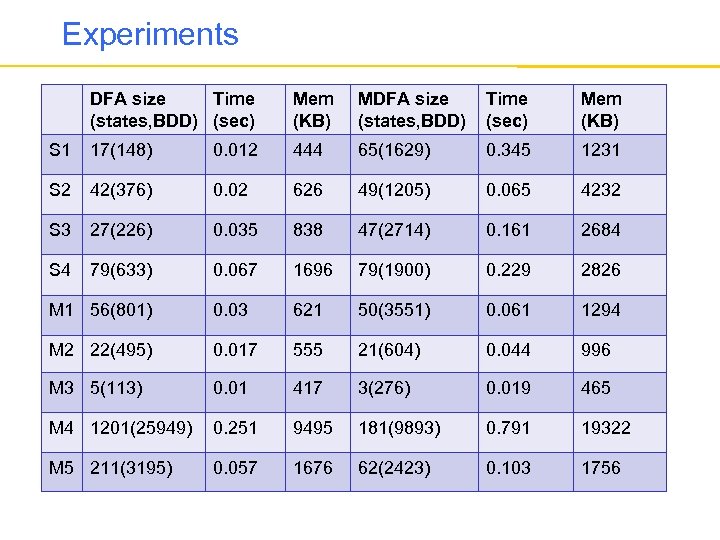
Experiments • XSS (Cross-Site Scripting) benchmarks (contain vulnerability) • We check whether the input to a sensitive function can contain the string