ecf6fc4c5bd90c479e43a9865e2302c8.ppt
- Количество слайдов: 82
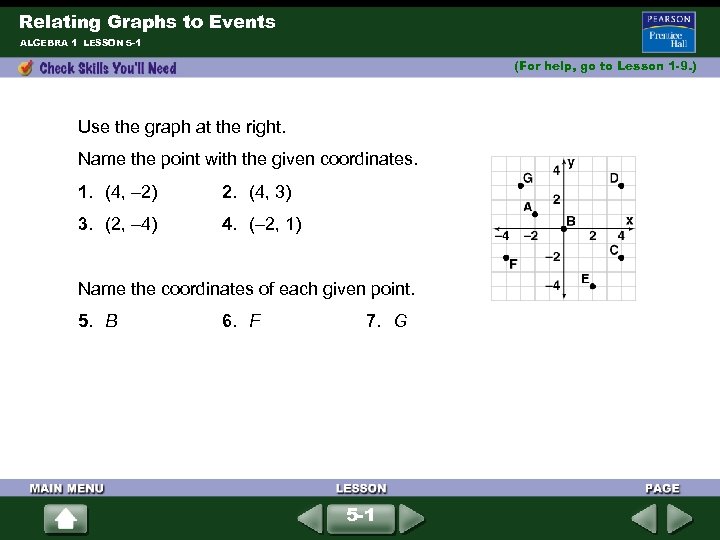
Relating Graphs to Events ALGEBRA 1 LESSON 5 -1 (For help, go to Lesson 1 -9. ) Use the graph at the right. Name the point with the given coordinates. 1. (4, – 2) 2. (4, 3) 3. (2, – 4) 4. (– 2, 1) Name the coordinates of each given point. 5. B 6. F 7. G 5 -1

Relating Graphs to Events ALGEBRA 1 LESSON 5 -1 Solutions 1. (4, – 2) is point C 2. (4, 3) is point D 3. (2, – 4) is point E 4. (– 2, 1) is point A 5. B coordinates: (0, 0) 6. F coordinates: (– 4, – 2) 7. G coordinates: (– 3, 3) 5 -1
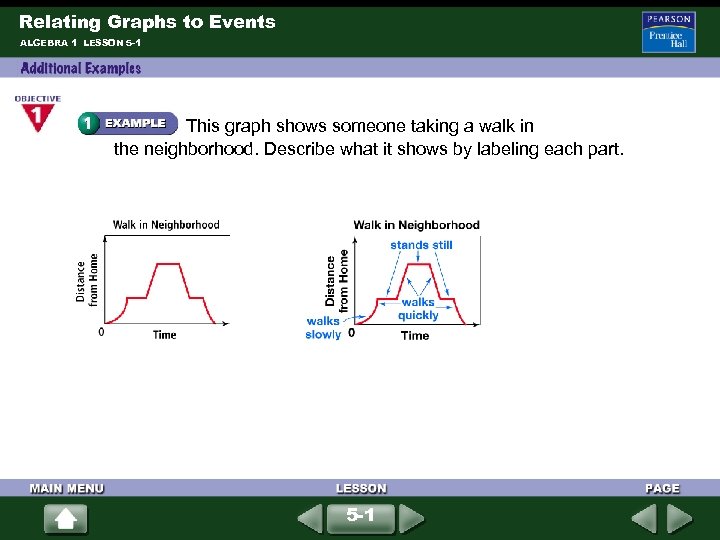
Relating Graphs to Events ALGEBRA 1 LESSON 5 -1 This graph shows someone taking a walk in the neighborhood. Describe what it shows by labeling each part. 5 -1

Relating Graphs to Events ALGEBRA 1 LESSON 5 -1 A pelican flies above the water searching for fish. Sketch a graph of its altitude from takeoff from shore to diving to the water to catch a fish. Label each section. 5 -1
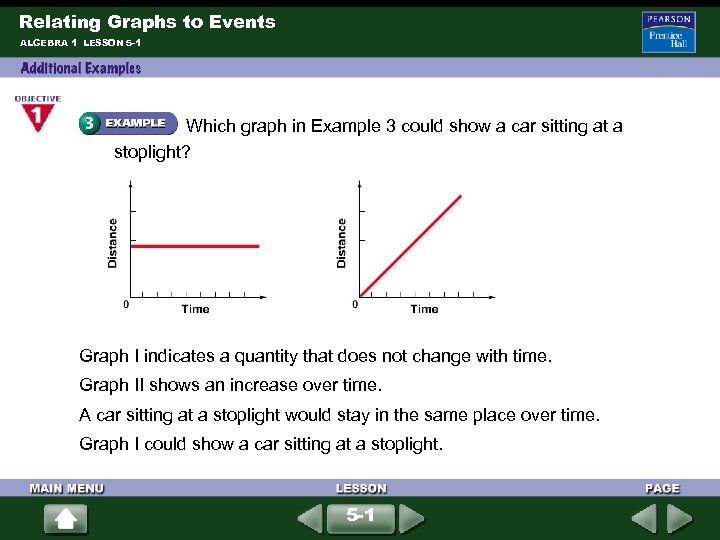
Relating Graphs to Events ALGEBRA 1 LESSON 5 -1 Which graph in Example 3 could show a car sitting at a stoplight? Graph I indicates a quantity that does not change with time. Graph II shows an increase over time. A car sitting at a stoplight would stay in the same place over time. Graph I could show a car sitting at a stoplight. 5 -1

Relating Graphs to Events ALGEBRA 1 LESSON 5 -1 pages 238– 240 Exercises 1– 4. Labels may vary. Samples are given. 1. 2. 3. 5. 4. 6. 5 -1

Relating Graphs to Events ALGEBRA 1 LESSON 5 -1 7. 9. C; the temperature increases steadily and then alternates cooling and warming as the oven turns off and on during a cooking cycle. 8. 10. The pressure dropped from 7 A. M. to 3 P. M. , stayed about the same until 9 P. M. , and then generally rose until 7 A. M. the next day. 11. a. b. No; the graphs are different because you have a constant speed traveling up but not down. 5 -1
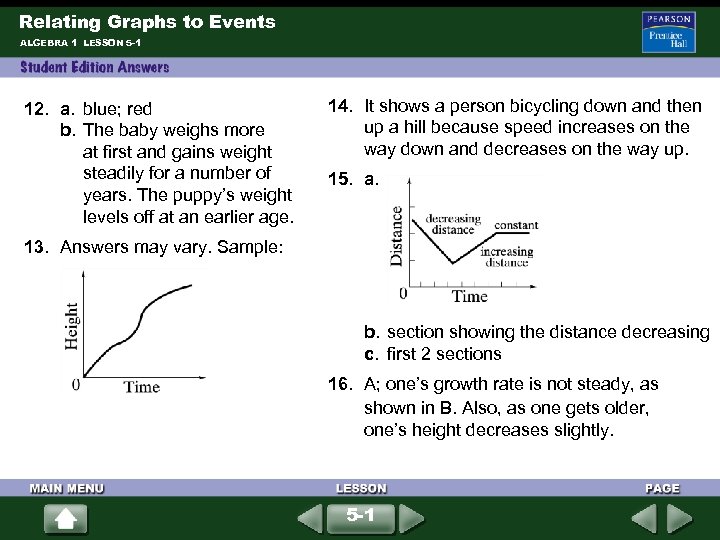
Relating Graphs to Events ALGEBRA 1 LESSON 5 -1 12. a. blue; red b. The baby weighs more at first and gains weight steadily for a number of years. The puppy’s weight levels off at an earlier age. 14. It shows a person bicycling down and then up a hill because speed increases on the way down and decreases on the way up. 15. a. 13. Answers may vary. Sample: b. section showing the distance decreasing c. first 2 sections 16. A; one’s growth rate is not steady, as shown in B. Also, as one gets older, one’s height decreases slightly. 5 -1

Relating Graphs to Events ALGEBRA 1 LESSON 5 -1 17. a. Check students’ work. b. A graph of temperatures at the equator would show little change for daily high temperatures. 18. $3 19. $6 22. a. Answers may vary. Sample: The student started skating and got to cruising speed. After a while, the student sped up going downhill, lost control, and crashed. After getting up, the student decided not to go as fast. b. Answers may vary. Sample: 20. more than 2 h up to 4 h 21. Answers may vary. Sample: Yes, the line segments make the graph look like steps. I–speeding up; II–cruising; III–crash; IV–slower speed 5 -1

Relating Graphs to Events ALGEBRA 1 LESSON 5 -1 23. D 24. H 25. [2] IV; the graph rises sharply at first and then slows. This indicates that the container is narrow at the bottom and wide at the top. [1] chooses correct graph but explanation is incomplete OR chooses the wrong graph but supports choice 26. 1 36 27. 1 36 28. 1 18 29. 1 41. – 15 12 1 30. 4 1 31. 6 42. – 16 43. 294 32. x < 7 33. x < 8 34. x – 2 > – 35. x > – 4 36. x – 13 < – 37. x < 2 3 38. 11 39. 17 40. 45 5 -1 44. 6 45. 3 46. 7 47. 41 48. 179 49. 1 4

Relating Graphs to Events ALGEBRA 1 LESSON 5 -1 Use the graph for questions 1– 3. 1. Why does this graph not start at zero? A person’s height is not zero when born. 2. Why is the graph not a straight slanted line? A straight line represents a constant rate of growth and people do not grow that way. 3. What does the flat part at the top of the graph represent? The person has stayed the same height over a long period of time. 4. Would a horizontal line, a straight slanted line, a curve, or a jagged curve best represent the calories you burn during the day? a jagged curve 5 -1

Relations and Functions ALGEBRA 1 LESSON 5 -2 (For help, go to Lessons 1– 9 and 1– 2. ) Graph each point on a coordinate plane. 1. (2, – 4) 2. (0, 3) 3. (– 1, – 2) 4. (– 3, 0) Evaluate each expression. 5. 3 a – 2 for a = – 5 x + 3 – 6 6. for x = 3 5 -2 7. 3 x 2 for x = 6
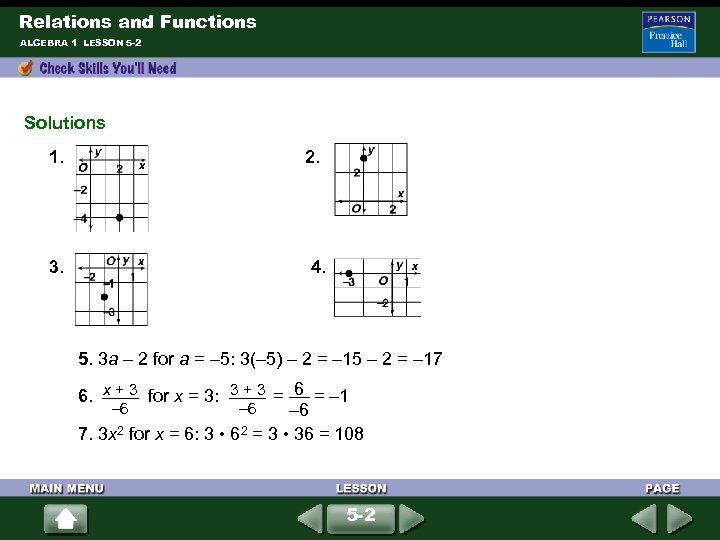
Relations and Functions ALGEBRA 1 LESSON 5 -2 Solutions 1. 3. 2. 4. 5. 3 a – 2 for a = – 5: 3(– 5) – 2 = – 15 – 2 = – 17 x + 3 3 + 3 6 6. for x = 3: = = – 1 – 6 – 6 7. 3 x 2 for x = 6: 3 • 62 = 3 • 36 = 108 5 -2
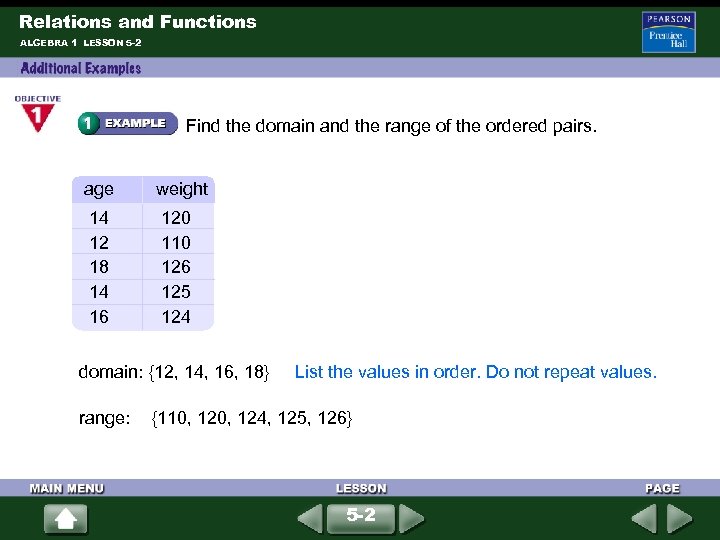
Relations and Functions ALGEBRA 1 LESSON 5 -2 Find the domain and the range of the ordered pairs. age weight 14 12 18 14 16 120 110 126 125 124 domain: {12, 14, 16, 18} List the values in order. Do not repeat values. range: {110, 124, 125, 126} 5 -2

Relations and Functions ALGEBRA 1 LESSON 5 -2 Use the vertical-line test to determine whether the relation {(3, 2), (5, – 1), (– 5, 3), (– 2, 2)} is a function. Step 1: Graph the ordered pairs on a coordinate plane. Step 2: Pass a pencil across the graph. Keep your pencil straight to represent a vertical line. A vertical line would not pass through more than one point, so the relation is a function. 5 -2

Relations and Functions ALGEBRA 1 LESSON 5 -2 Determine whether each relation is a function. a. {(4, 3), (2, – 1), (– 3, – 3), (2, 4)} The domain value 2 corresponds to two range values, – 1 and 4. The relation is not a function. b. {(– 4, 0), (2, 12), (– 1, – 3), (1, 5)} There is no value in the domain that corresponds to more than one value of the range. The relation is a function. 5 -2
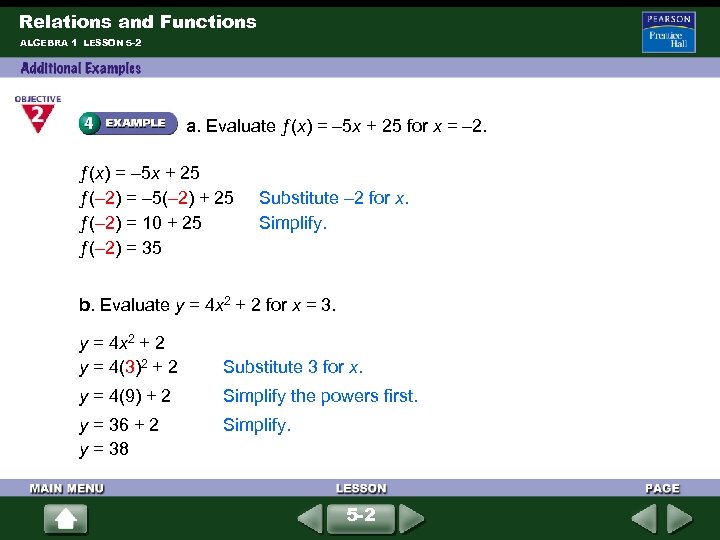
Relations and Functions ALGEBRA 1 LESSON 5 -2 a. Evaluate ƒ(x) = – 5 x + 25 for x = – 2. ƒ(x) = – 5 x + 25 ƒ(– 2) = – 5(– 2) + 25 ƒ(– 2) = 10 + 25 ƒ(– 2) = 35 Substitute – 2 for x. Simplify. b. Evaluate y = 4 x 2 + 2 for x = 3. y = 4 x 2 + 2 y = 4(3)2 + 2 Substitute 3 for x. y = 4(9) + 2 Simplify the powers first. y = 36 + 2 y = 38 Simplify. 5 -2
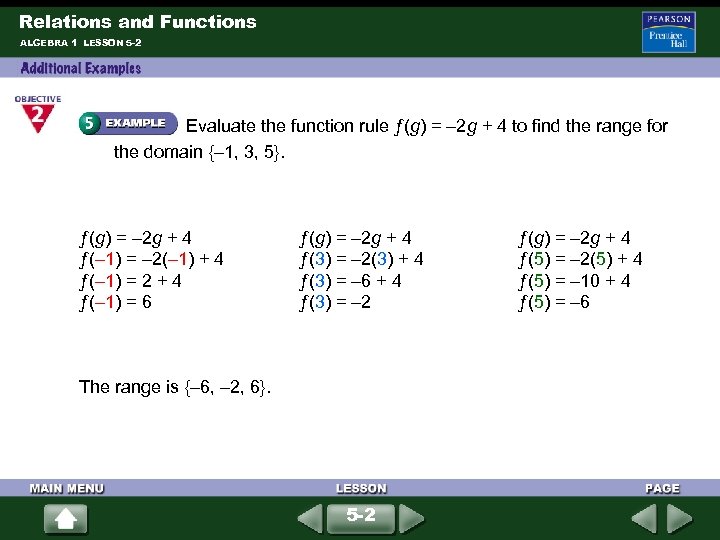
Relations and Functions ALGEBRA 1 LESSON 5 -2 Evaluate the function rule ƒ(g) = – 2 g + 4 to find the range for the domain {– 1, 3, 5}. ƒ(g) = – 2 g + 4 ƒ(– 1) = – 2(– 1) + 4 ƒ(– 1) = 2 + 4 ƒ(– 1) = 6 ƒ(g) = – 2 g + 4 ƒ(3) = – 2(3) + 4 ƒ(3) = – 6 + 4 ƒ(3) = – 2 The range is {– 6, – 2, 6}. 5 -2 ƒ(g) = – 2 g + 4 ƒ(5) = – 2(5) + 4 ƒ(5) = – 10 + 4 ƒ(5) = – 6

Relations and Functions ALGEBRA 1 LESSON 5 -2 pages 244– 246 Exercises 12. no 24. {– 8, – 2, 18} 1. {4, 5, 6}, {3, 6, 7, 19} 13. yes 25. {– 27, – 2, 8, 48} 2. {– 3, – 2, 0, 4}, {5, 7, 8, 22} 14. no 26. {– 4 , – , 0} 3. {– 2, 2, 3}, {– 3, – 2, 3} 15. 4 27. no 4. {1}, {– 7, 0, 5, 6. 1, 10} 16. – 34 28. no 5. {– 3. 1, 1. 2, 8. 4}, {– 5. 2, 0, 4} 17. 9 29. yes; {– 4, – 1, 0, 3}; {– 4} 2 1 3 6. {– , , 4, 5}, {– 1, 0, } 18. 12 7. yes 19. 18 30. No; two 4 -year-old iguanas may have different lengths. 8. no 20. – 7 9. no 21. – 3 10. yes 22. 5 11. no 23. {0. 5, 53} 3 2 5 4 5 -2 1 2 3 4 31. Answers may vary. Sample: A relation is not a function if two range values have the same domain value.

Relations and Functions ALGEBRA 1 LESSON 5 -2 32. a. {– 300, – 210, 0, 72} b. Domain is the number of cameras sold, and range is the profit. 38. yes 33. Answers may vary. Sample: 41. a. Answers may vary. Sample: The cost appears to be far too little. Data represent the ages (x) and heights (y) of 4 students. 34. {– 3, 3, 15. 8} 35. {– 13. 8, – 1, 5} 36. {– 0. 5, 0, 2. 7} 39. no 40. yes b. Answers may vary. Sample: The student failed to convert hours to minutes. c. $10. 80 d. whole numbers; positive numbers 42. a. 3, 720, 000 mi b. 11, 160, 000 mi 37. {– 0. 75, 0, 12. 69} 5 -2
![Relations and Functions ALGEBRA 1 LESSON 5 -2 43. 23 53. [2] 44. 18 Relations and Functions ALGEBRA 1 LESSON 5 -2 43. 23 53. [2] 44. 18](https://present5.com/presentation/ecf6fc4c5bd90c479e43a9865e2302c8/image-21.jpg)
Relations and Functions ALGEBRA 1 LESSON 5 -2 43. 23 53. [2] 44. 18 45. 6 46. 20 Yes, the data represent a function. (OR graph shown) [1] shows calculation but no mapping diagram or graph 47. Yes, it passes the vertical line test; no, it doesn’t pass the vertical line test. 48. a. 0, – 1, – 2, – 6 b. all integers 54. Labels may vary. Sample: 49. 5. 25 50. 8. 7 51. – 3 52. 3 5 -2

Relations and Functions ALGEBRA 1 LESSON 5 -2 55. 30 mi 56. 22. 5 mi 57. 7. 5 mi 58. 48. 75 mi 59. 82. 5 mi 60. 108. 75 mi 61. 33. 5, none, 3 1 62. – , 0, – 2 and 1, 4 5 63. 52 , 5, 5, 11 9 64. 117 , 14, 13, 11 8 47 65. – , – 7, 8 8 66. 46. 5, 43 and 48, 10 5 -2

Relations and Functions ALGEBRA 1 LESSON 5 -2 1. a. Find the domain and range of the ordered pairs (1, 3), (– 4, 0), (3, 1), (0, 4), (2, 3). domain: {– 4, 0, 1, 2, 3} range: {0, 1, 3, 4} b. Use mapping to determine whether the relation is a function. The relation is a function. 2. Use the vertical-line test a. to determine whether each relation is a function. b. no yes 3. Find the range of the function ƒ(g) = 3 g – 5 for the domain {– 1. 5, 2, 4}. {– 9. 5, 1, 7} 5 -2
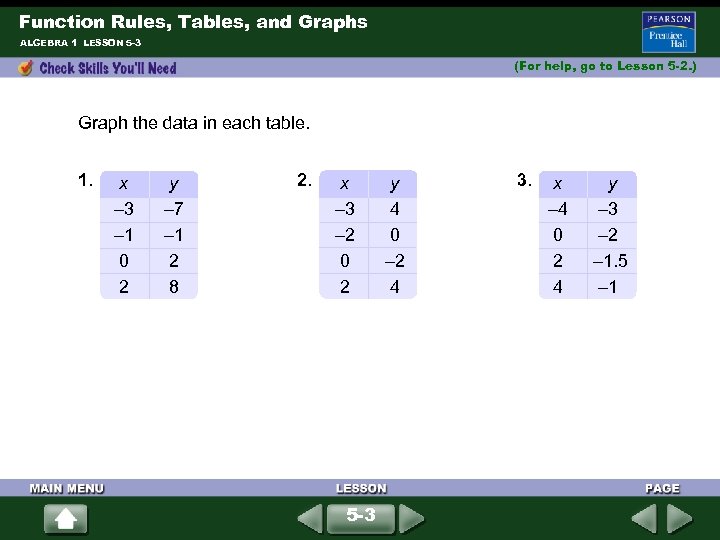
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 (For help, go to Lesson 5 -2. ) Graph the data in each table. 1. x – 3 – 1 0 2 y – 7 – 1 2 8 2. x – 3 – 2 0 2 5 -3 y 4 0 – 2 4 3. x – 4 0 2 4 y – 3 – 2 – 1. 5 – 1
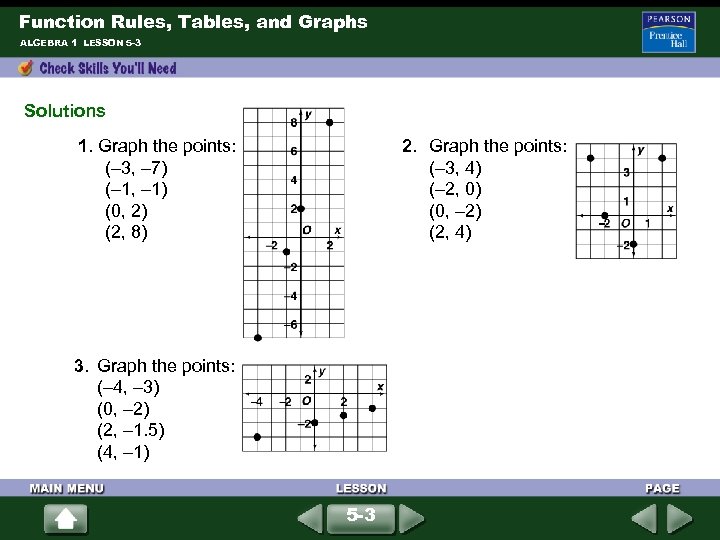
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 Solutions 1. Graph the points: (– 3, – 7) (– 1, – 1) (0, 2) (2, 8) 2. Graph the points: (– 3, 4) (– 2, 0) (0, – 2) (2, 4) 3. Graph the points: (– 4, – 3) (0, – 2) (2, – 1. 5) (4, – 1) 5 -3
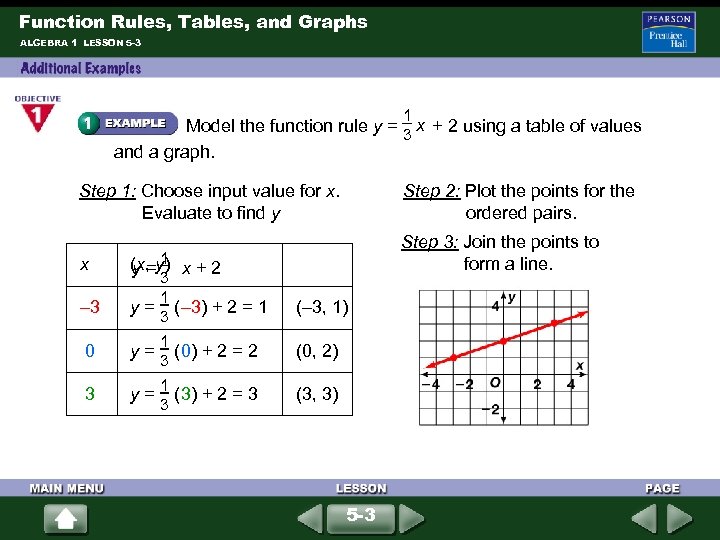
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 1 x Model the function rule y = + 2 using a table of values 3 and a graph. Step 1: Choose input value for x. Evaluate to find y Step 2: Plot the points for the ordered pairs. Step 3: Join the points to form a line. x 1 (x, y) y = x + 2 3 – 3 y = (– 3) + 2 = 1 3 0 y = (0) + 2 = 2 (0, 2) 3 1 y = (3) + 2 = 3 (3, 3) 1 1 3 3 (– 3, 1) 5 -3
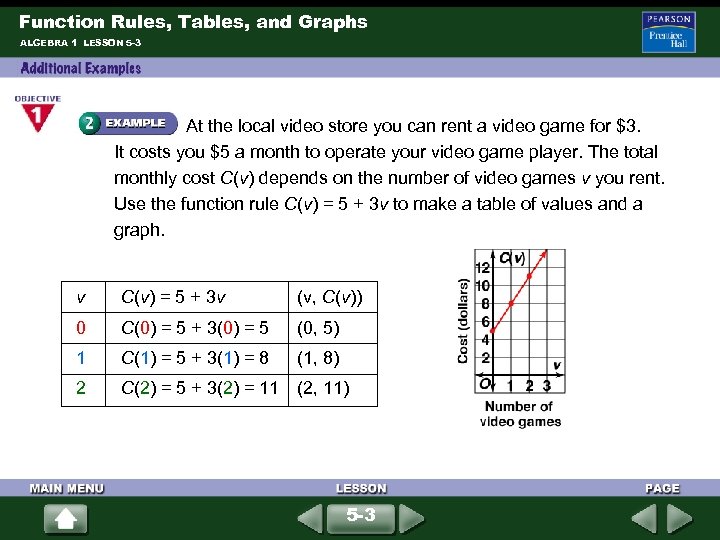
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 At the local video store you can rent a video game for $3. It costs you $5 a month to operate your video game player. The total monthly cost C(v) depends on the number of video games v you rent. Use the function rule C(v) = 5 + 3 v to make a table of values and a graph. v C(v) = 5 + 3 v (v, C(v)) 0 C(0) = 5 + 3(0) = 5 (0, 5) 1 C(1) = 5 + 3(1) = 8 (1, 8) 2 C(2) = 5 + 3(2) = 11 (2, 11) 5 -3
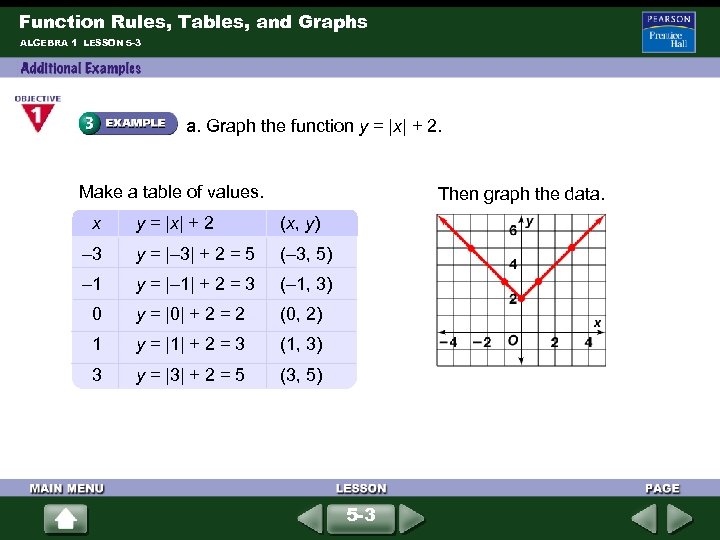
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 a. Graph the function y = |x| + 2. Make a table of values. Then graph the data. x y = |x| + 2 (x, y) – 3 y = |– 3| + 2 = 5 (– 3, 5) – 1 y = |– 1| + 2 = 3 (– 1, 3) 0 y = |0| + 2 = 2 (0, 2) 1 y = |1| + 2 = 3 (1, 3) 3 y = |3| + 2 = 5 (3, 5) 5 -3
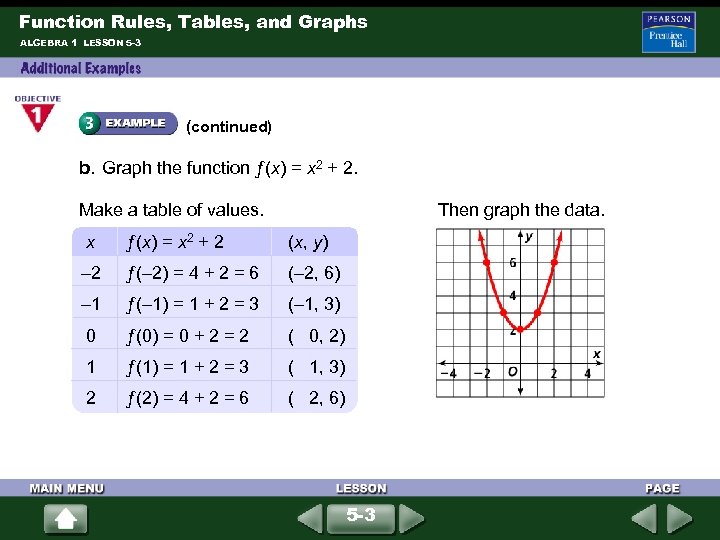
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 (continued) b. Graph the function ƒ(x) = x 2 + 2. Make a table of values. Then graph the data. x ƒ(x) = x 2 + 2 (x, y) – 2 ƒ(– 2) = 4 + 2 = 6 (– 2, 6) – 1 ƒ(– 1) = 1 + 2 = 3 (– 1, 3) 0 ƒ(0) = 0 + 2 = 2 ( 0, 2) 1 ƒ(1) = 1 + 2 = 3 ( 1, 3) 2 ƒ(2) = 4 + 2 = 6 ( 2, 6) 5 -3
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 pages 249– 252 Exercises 5. 7. 6. 8. 1. C 2. A 3. B 4– 12. Tables may vary. Samples are given. 4. 5 -3
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 9. 11. 10. 12. 13. a. M = 3. 5 h b–d. Answers may vary. Samples are given. b. c. d. about 8. 5 h 5 -3
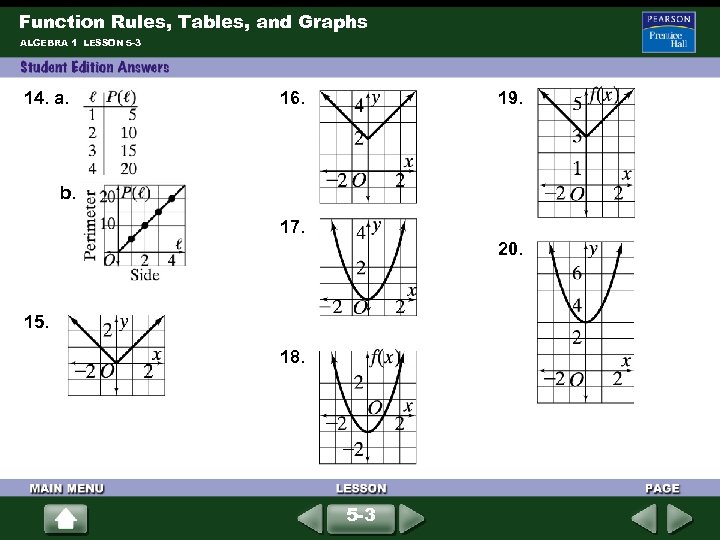
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 14. a. 16. 19. b. 17. 20. 15. 18. 5 -3
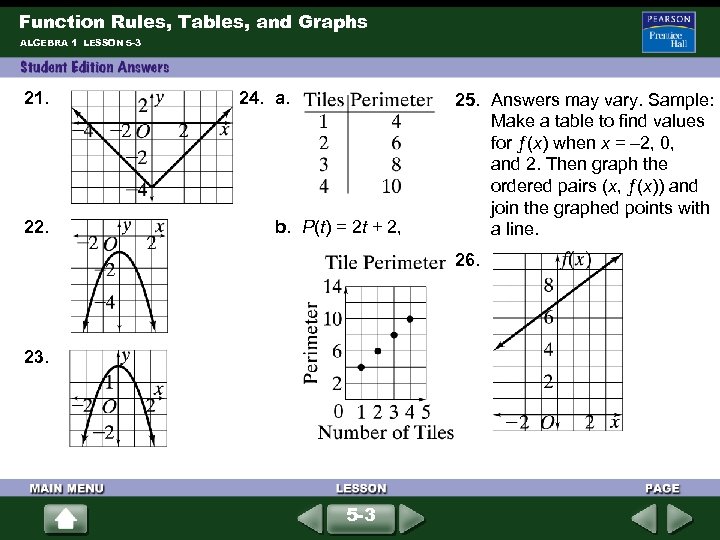
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 21. 22. 24. a. b. P(t) = 2 t + 2, 25. Answers may vary. Sample: Make a table to find values for ƒ(x) when x = – 2, 0, and 2. Then graph the ordered pairs (x, ƒ(x)) and join the graphed points with a line. 26. 23. 5 -3
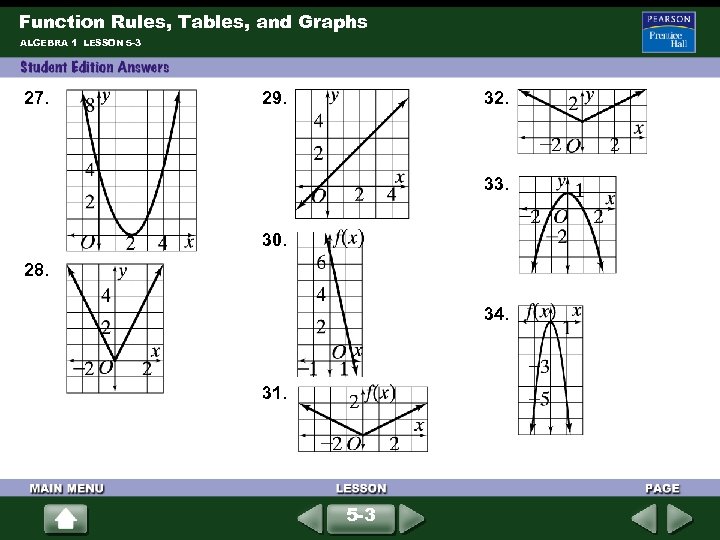
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 27. 32. 29. 33. 30. 28. 34. 31. 5 -3
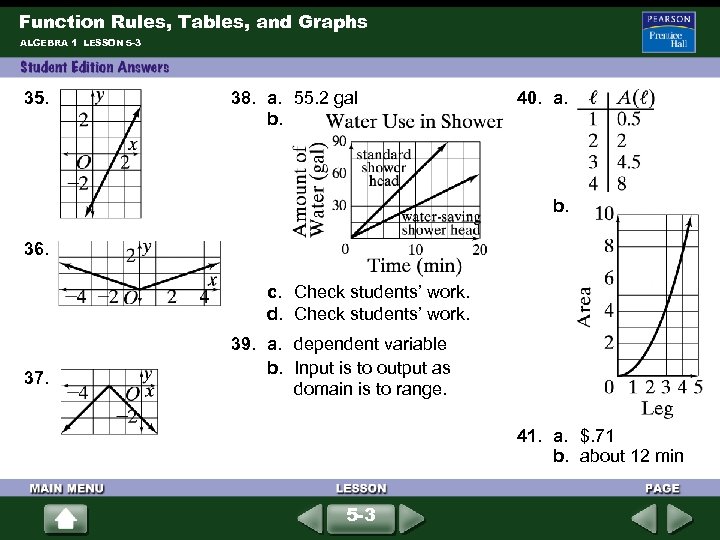
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 35. 38. a. 55. 2 gal b. 40. a. b. 36. c. Check students’ work. d. Check students’ work. 37. 39. a. dependent variable b. Input is to output as domain is to range. 41. a. $. 71 b. about 12 min 5 -3
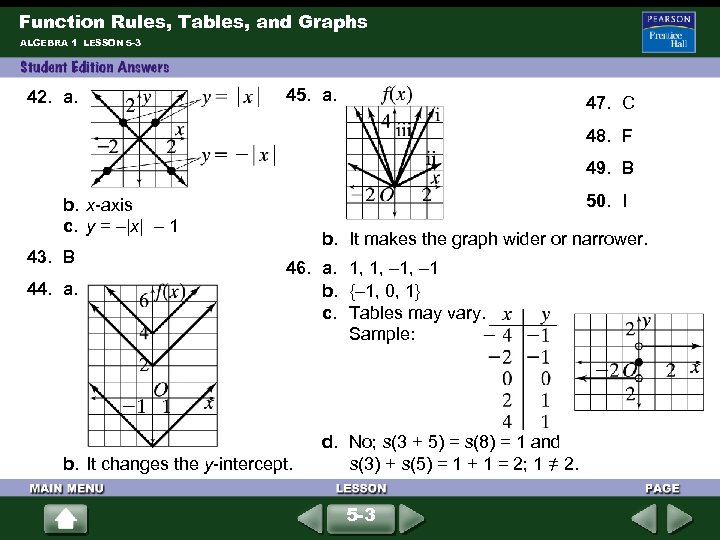
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 42. a. 45. a. 47. C 48. F 49. B 50. I b. It makes the graph wider or narrower. b. x-axis c. y = –|x| – 1 43. B 44. a. 46. a. 1, 1, – 1 b. {– 1, 0, 1} c. Tables may vary. Sample: b. It changes the y-intercept. d. No; s(3 + 5) = s(8) = 1 and s(3) + s(5) = 1 + 1 = 2; 1 = 2. / 5 -3
![Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 51. [2] 52. [4] Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 51. [2] 52. [4]](https://present5.com/presentation/ecf6fc4c5bd90c479e43a9865e2302c8/image-37.jpg)
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 51. [2] 52. [4] a. Tables may vary. Sample: b. The graphs of all equations go through the point (0, 3). y = x + 3 and y = x 2 + 3 share points on the [3] appropriate methods but one right side of the y-axis. Both sides calculation error of the graphs y = x 2 + 3 and y = |x|+ 3 go upward, but y = |x| + 3 has straight lines [2] correct table but an error in graph and y = x 2 + 3 has curved lines. [1] table with no graph OR graph [1] at least two of the graphs drawn correctly with no table 5 -3

Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 53. {– 5, 1, 11. 5} 64. – 3. 6, 3. 6 54. {– 11, – 5, 5. 5} 65. – 7, 7 55. {– 6. 5, 4, 10} 66. – 7, 7 56. {– 5, – 3, – 1. 5} 67. 4, – 2 57. {8. 5, 12, 14} 68. – 7, – 15 58. {– 20, – 10, 7. 5} 69. 1. 5, – 0. 5 59. {– 11, 1, 22} 70. – 1, – 7 60. {– 9, – 8, – 6. 25} 71. 48 km 61. {– 29. 5, 9, 31} 72. 40 km 62. 4, – 4 73. 100. 8 km 63. No sol. ; 9 = 10 – 1 and |b| cannot be – 1. 74. 136 km 75. 163. 2 km 5 -3 76. a. 7 = x , 25. 375 ft 8 29 b. 7 = x , 31. 35 ft 8 35. 833 7 x c. = , 16. 1875 ft 8 18. 5
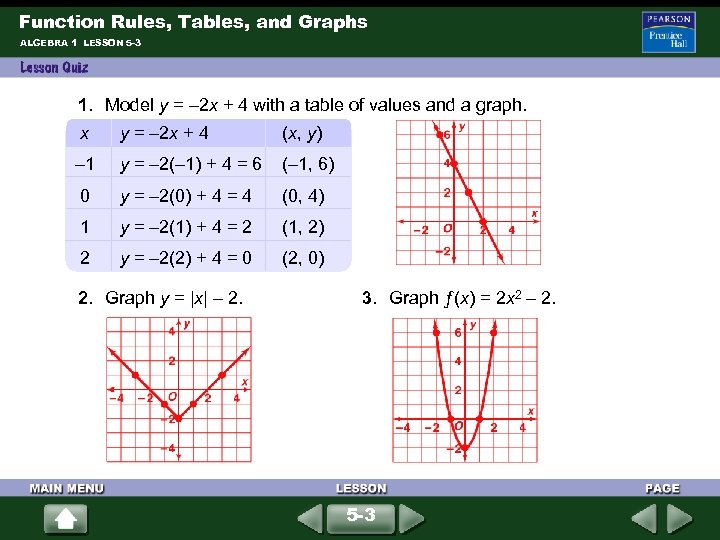
Function Rules, Tables, and Graphs ALGEBRA 1 LESSON 5 -3 1. Model y = – 2 x + 4 with a table of values and a graph. x y = – 2 x + 4 (x, y) – 1 y = – 2(– 1) + 4 = 6 (– 1, 6) 0 y = – 2(0) + 4 = 4 (0, 4) 1 y = – 2(1) + 4 = 2 (1, 2) 2 y = – 2(2) + 4 = 0 (2, 0) 2. Graph y = |x| – 2. 3. Graph ƒ(x) = 2 x 2 – 2. 5 -3

Writing a Function Rule ALGEBRA 1 LESSON 5 -4 (For help, go to Lesson 5 -3. ) Model each rule with a table of values. 1. f(x) = 5 x – 1 2. y = – 3 x + 4 3. g(t) = 0. 2 t – 7 4. y = 4 x + 1 5. f(x) = 6 – x 6. c(d) = d + 0. 9 Evaluate each function rule for n = 2. 7. A(n) = 2 n – 1 8. f(n) = – 3 + n – 1 5 -4 9. g(n) = 6 – n

Writing a Function Rule ALGEBRA 1 LESSON 5 -4 Solutions 1. 2. 3. 4. 5. 6. 5 -4
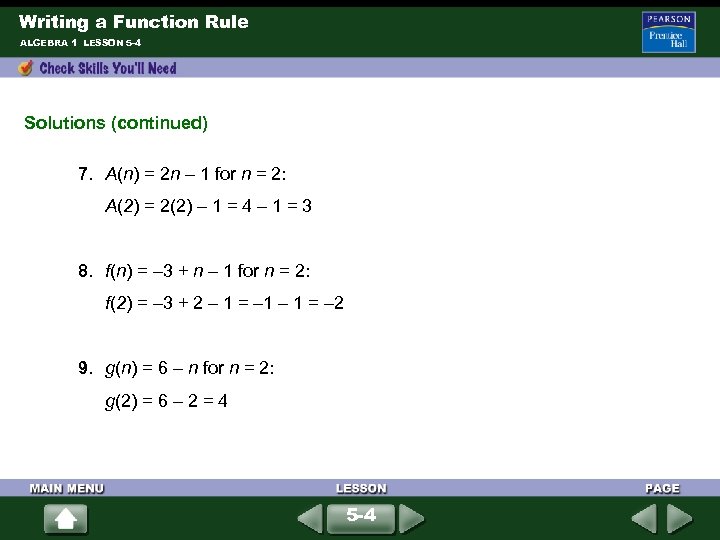
Writing a Function Rule ALGEBRA 1 LESSON 5 -4 Solutions (continued) 7. A(n) = 2 n – 1 for n = 2: A(2) = 2(2) – 1 = 4 – 1 = 3 8. f(n) = – 3 + n – 1 for n = 2: f(2) = – 3 + 2 – 1 = – 2 9. g(n) = 6 – n for n = 2: g(2) = 6 – 2 = 4 5 -4
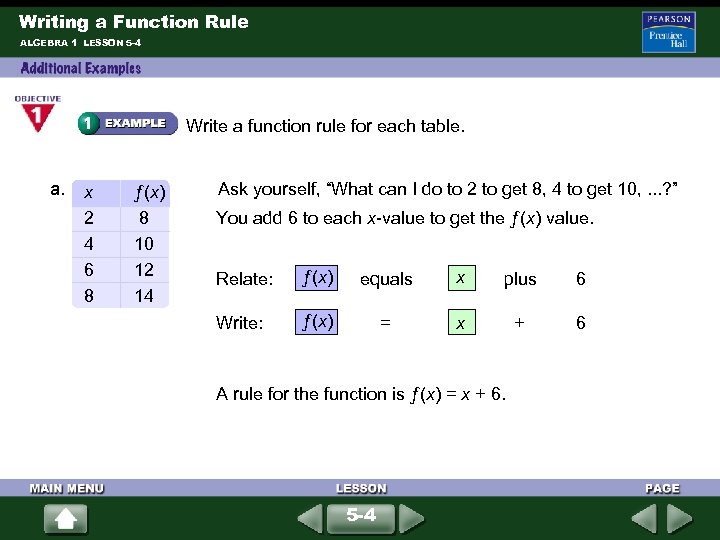
Writing a Function Rule ALGEBRA 1 LESSON 5 -4 Write a function rule for each table. a. x 2 4 6 8 ƒ(x) 8 10 12 14 Ask yourself, “What can I do to 2 to get 8, 4 to get 10, . . . ? ” You add 6 to each x-value to get the ƒ(x) value. Relate: ƒ(x) Write: ƒ(x) equals x plus 6 = x + 6 A rule for the function is ƒ(x) = x + 6. 5 -4
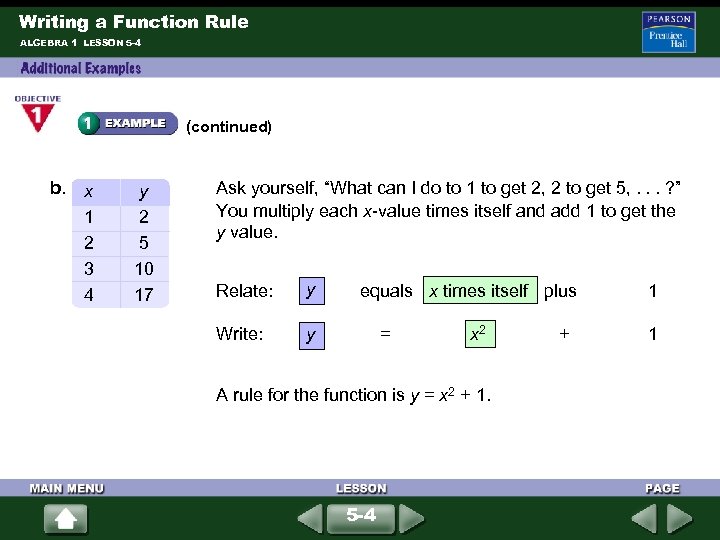
Writing a Function Rule ALGEBRA 1 LESSON 5 -4 (continued) b. x 1 2 3 4 y 2 5 10 17 Ask yourself, “What can I do to 1 to get 2, 2 to get 5, . . . ? ” You multiply each x-value times itself and add 1 to get the y value. Relate: y equals x times itself plus Write: y = x 2 + A rule for the function is y = x 2 + 1. 5 -4 1 1

Writing a Function Rule ALGEBRA 1 LESSON 5 -4 The journalism class makes $25 per page of advertising in the yearbook. If the class sells n pages, how much money will it earn? a. Write a function rule to describe this relationship. Relate: money earned is 25 times number of pages sold n Define: Let = number of pages sold. P(n) Let = money earned. Write: P(n) = 25 • n The function rule P(n) = 25 n describes the relationship between the number of pages sold and the money earned. 5 -4

Writing a Function Rule ALGEBRA 1 LESSON 5 -4 (continued) b. The class sold 6 pages of advertising. How much money did the class make? P(n) = 25 • n P(6) = 25 • 6 Substitute 6 for n. P(6) = 150 Simplify. The class made $150. 5 -4
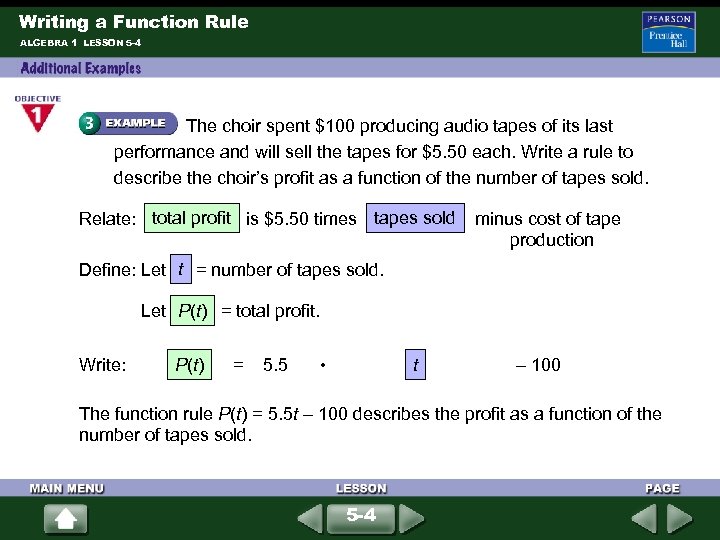
Writing a Function Rule ALGEBRA 1 LESSON 5 -4 The choir spent $100 producing audio tapes of its last performance and will sell the tapes for $5. 50 each. Write a rule to describe the choir’s profit as a function of the number of tapes sold. Relate: total profit is $5. 50 times tapes sold minus cost of tape production t Define: Let = number of tapes sold. P(t) Let = total profit. Write: P(t) t = 5. 5 • – 100 The function rule P(t) = 5. 5 t – 100 describes the profit as a function of the number of tapes sold. 5 -4

Writing a Function Rule ALGEBRA 1 LESSON 5 -4 pages 256– 259 Exercises 1 1. B 12. ƒ(h) = h 12 2. A 13. e(n) = 6. 37 n 3. C 14. A(n) = n 2 4. ƒ(x) = 3 x 15. V(n) = n 3 5. ƒ(x) = x – 0. 5 16. A(r) = r 2 6. ƒ(x) = 0. 5 x 17. a. ƒ(x) = 0. 19 x b. $1. 52 7. ƒ(x) = – 3 x 8. y = 4 x 9. y = x 2 10. t(c) = 0. 79 c 21. a. C(a) = 10 a + 1 b. $31 c. 61; the total cost of 12 books 22. a. C(b) = 6 b b. 72; the total cost of 12 books c. about $5. 08 d. Club; $61 is less than $72. 18. a. ƒ(x) = 0. 34 + 0. 21(x – 1) 23. Answers may vary. b. $. 97 Sample: The input 19. ƒ(x) = 1000 x values you need may not be in the table. 20. ƒ(x) = 2. 54 x 11. d(n) = 45 n 5 -4

Writing a Function Rule ALGEBRA 1 LESSON 5 -4 24. a. gal of water, number 26. of loads b. w(n) = 34 n c. 238 gal 3 d. 13 loads y = x + 3 25– 28. Tables may vary. Samples are given. 27. 2 25. 29. Answers may vary. Sample: ƒ(x) = 60 x; ƒ(3) = 180, 180 mi in 3 h, the distance you can travel at a constant speed of 60 mi/h 30. a. 0. 15 b b. c(b) = 1. 15 b c. $20. 70 31. ƒ(x) = x 3 32. ƒ(x) = –x 3 y = –x + 2 1 ƒ(x) = x 28. 2 2 y = x 3 5 -4 33. ƒ(x) = –x 3 – 1 34. a. b. c. d. c(m) = 44 + 0. 38 m $70. 60, $89. 60 38 mi $202
Writing a Function Rule ALGEBRA 1 LESSON 5 -4 35. a. B(v) = 6. 93 v 7 b. B(w) = w 36. A 10 42– 47. Tables may vary. Samples are given. 42. 37. H 38. D 39. B 40. C 41. [2] D = 0. 1 w 2 + 5 w 43. D = 0. 1(60)2 + 5(60) D = 0. 1(3600) + 300 D = 660 The dosage is 660 mg. [1] correctly substitutes 60 for w but makes a minor calculation error 5 -4
Writing a Function Rule ALGEBRA 1 LESSON 5 -4 44. 46. 48. 17%; increase 49. 2%; increase 50. 8%; decrease 51. 83%; decrease 52. 29%; increase 45. 47. 53. 42%; decrease 54. a. 2 oranges; 3 oranges b. 28 tbsp 5 -4

Writing a Function Rule ALGEBRA 1 LESSON 5 -4 1. Write a function rule for each table. a. x b. x y – 1 0 1 2 – 5 0 5 10 y = 5 x – 1 0 1 2 ƒ(x) – 4 – 3 – 2 – 1 ƒ(x) = x – 3 2. Write a function rule to describe each relationship. a. the total cost T(c) of c pounds of apples at $. 82 a pound T(c) = 0. 82 c b. a scale model s of a moth m that is 6 times the actual size of the moth s(m) = 6 m 3. You borrow $60 to buy a bread-making machine. You charge customers $1. 50 a loaf for your special bread. Write a rule to describe your profit as a function of the number n of loaves sold. P(n) = 1. 5 n - 60 5 -4
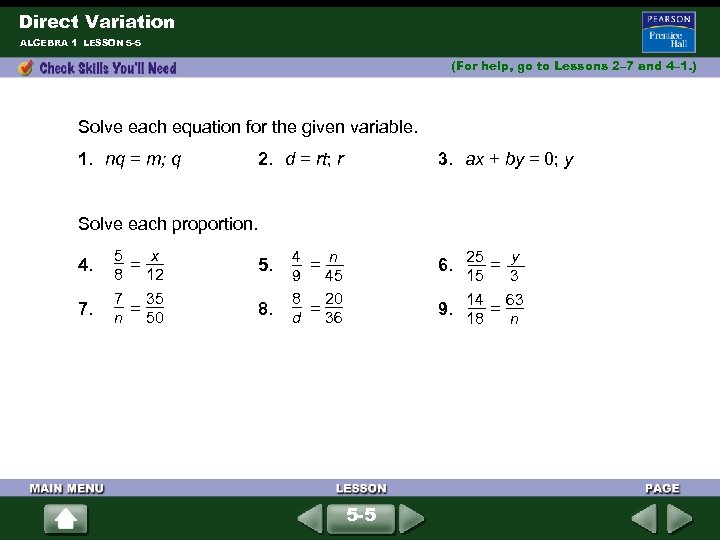
Direct Variation ALGEBRA 1 LESSON 5 -5 (For help, go to Lessons 2– 7 and 4– 1. ) Solve each equation for the given variable. 1. nq = m; q 2. d = rt; r 3. ax + by = 0; y Solve each proportion. 5 x 7 35 4. = 12 8 7. = 50 n 4 n 9 45 8 20 8. = 36 d 25 y 15 3 14 63 9. = 18 n 5. = 6. = 5 -5
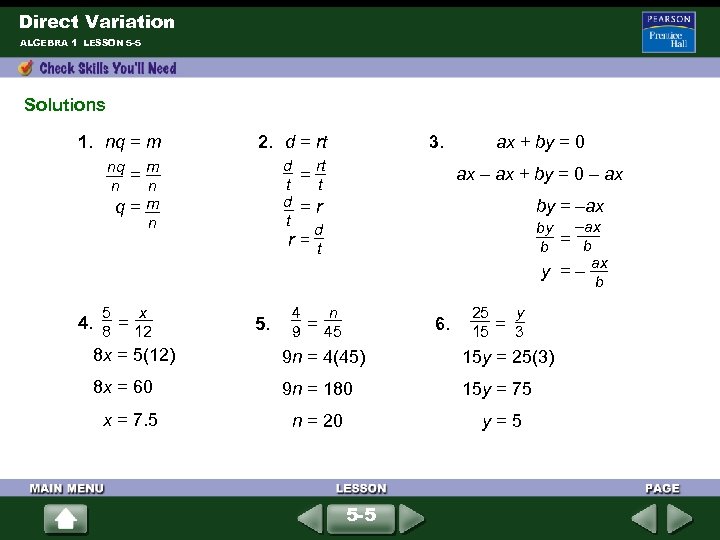
Direct Variation ALGEBRA 1 LESSON 5 -5 Solutions 1. nq = m 3. ax + by = 0 2. d = rt d rt = t t d = r t d r = t n q = m n n 5 x 4. = 12 8 8 x = 5(12) 4 ax – ax + by = 0 – ax by = –ax by –ax = b b ax y = – b n 5. = 45 9 9 n = 4(45) 25 y 6. = 3 15 15 y = 25(3) 8 x = 60 9 n = 180 15 y = 75 x = 7. 5 n = 20 y = 5 5 -5

Direct Variation ALGEBRA 1 LESSON 5 -5 Solutions (continued) 7 35 7. = 50 n 35 n = 7(50) 35 n = 350 n = 10 8 20 8. = 36 d 20 d = 8(36) 20 d = 288 d = 14. 4 5 -5 14 63 9. = n 18 14 n = 18(63) 14 n = 1134 n = 81
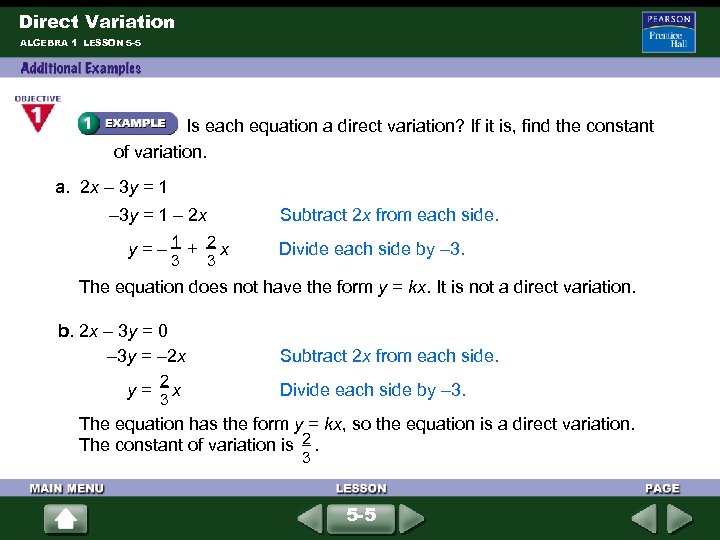
Direct Variation ALGEBRA 1 LESSON 5 -5 Is each equation a direct variation? If it is, find the constant of variation. a. 2 x – 3 y = 1 – 2 x Subtract 2 x from each side. 1 2 y = – + x Divide each side by – 3. 3 3 The equation does not have the form y = kx. It is not a direct variation. b. 2 x – 3 y = 0 – 3 y = – 2 x 2 3 y = x Subtract 2 x from each side. Divide each side by – 3. The equation has the form y = kx, so the equation is a direct variation. 2 The constant of variation is . 3 5 -5

Direct Variation ALGEBRA 1 LESSON 5 -5 Write an equation for the direct variation that includes the point (– 3, 2). y = kx Use the general form of a direct variation. 2 = k(– 3) Substitute – 3 for x and 2 for y. 2 – = k 3 Divide each side by – 3 to solve for k. 2 y = – x 3 2 Write an equation. Substitute – for k in y = kx. 3 2 The equation of the direct variation is y = – x. 3 5 -5
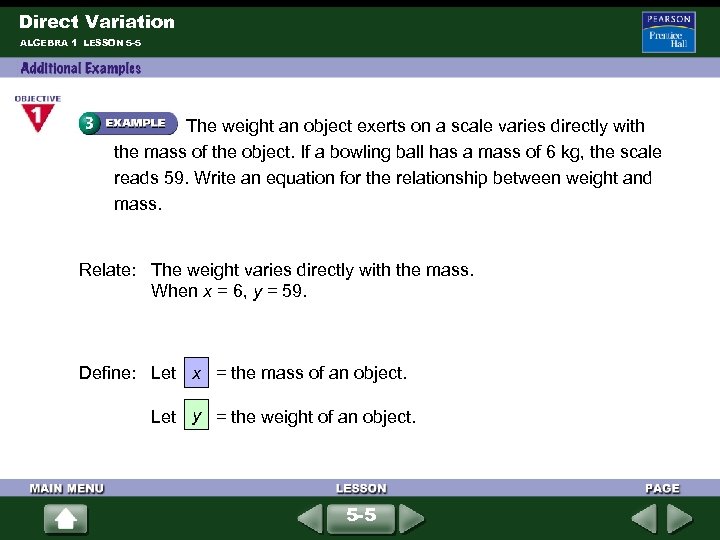
Direct Variation ALGEBRA 1 LESSON 5 -5 The weight an object exerts on a scale varies directly with the mass of the object. If a bowling ball has a mass of 6 kg, the scale reads 59. Write an equation for the relationship between weight and mass. Relate: The weight varies directly with the mass. When x = 6, y = 59. x Define: Let = the mass of an object. y Let = the weight of an object. 5 -5
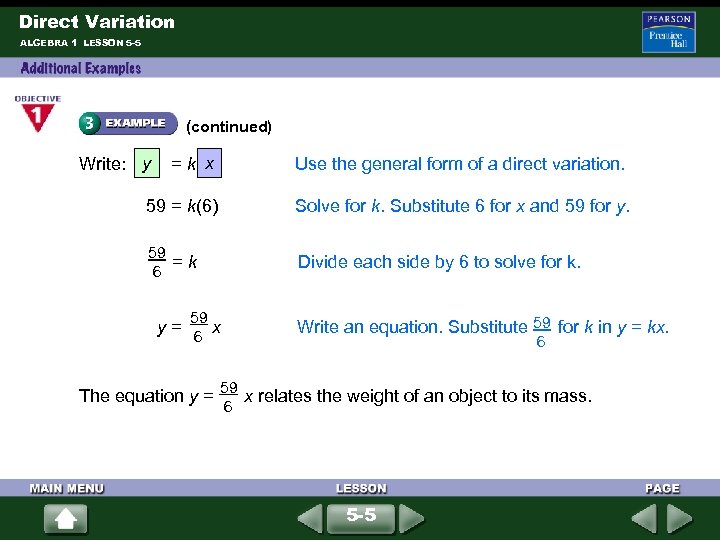
Direct Variation ALGEBRA 1 LESSON 5 -5 (continued) y Write: = k x Use the general form of a direct variation. 59 = k(6) Solve for k. Substitute 6 for x and 59 for y. 59 = k 6 Divide each side by 6 to solve for k. 59 59 Write an equation. Substitute for k in y = kx. y = x 6 6 59 The equation y = x relates the weight of an object to its mass. 6 5 -5
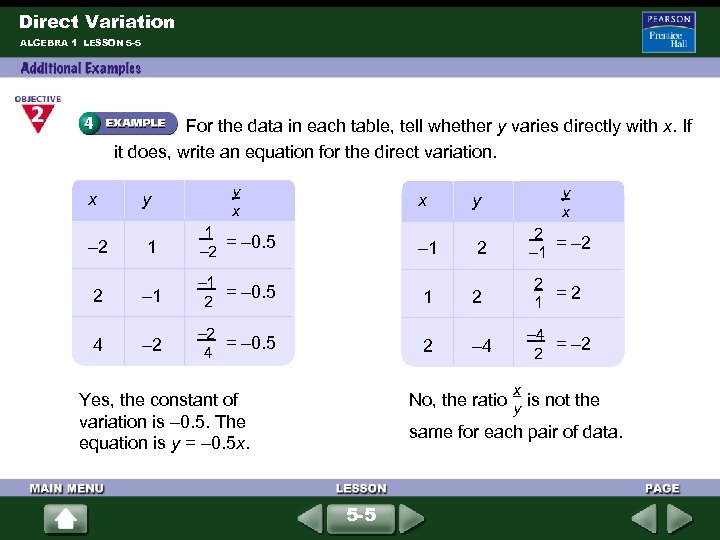
Direct Variation ALGEBRA 1 LESSON 5 -5 For the data in each table, tell whether y varies directly with x. If it does, write an equation for the direct variation. y y x 1 1 = – 0. 5 – 2 – 1 2 2 = – 2 – 1 – 1 = – 0. 5 2 1 2 2 = 2 1 4 – 2 = – 0. 5 4 2 – 4 x – 2 x y – 4 = – 2 2 x Yes, the constant of variation is – 0. 5. The equation is y = – 0. 5 x. No, the ratio is not the y same for each pair of data. 5 -5

Direct Variation ALGEBRA 1 LESSON 5 -5 Suppose a windlass requires 0. 75 lb of force to lift an object that weighs 48 lb. How much force would you need to lift 210 lb? Relate: The force of 0. 75 lb lifts 48 lb. The force of n lb lifts 210 lb. Define: Let n = the force you need to lift 210 lb. Write: force 1 force 2 = weight 1 weight 2 0. 75 n = 210 48 0. 75(210) = 48 n n 3. 3 Use a proportion. Substitute 0. 75 force 1, 48 for weight 1, and 210 for weight 2. Use cross products. Solve for n. You need about 3. 3 lb of force to lift 210 lb. 5 -5

Direct Variation ALGEBRA 1 LESSON 5 -5 pages 264– 267 Exercises 22– 23. Choices of variables may vary. 1. no 5 12. y = – x 2. no 13. y = x 5 23. E(h) = 7. 10 h 3. yes; – 2 3 14. y = – x 24. yes; y = 1. 8 x 9 4. no 15. 5. yes; 5 6 6. yes; 7 3 16. 7. yes; – 1 10 8. yes; 0. 5 17. 18. 22. P( ) = 8 4 2 1 y = – x 6 4 y = – x 3 9. yes; – 3 27. a. 50 or 5 20 2 130 b. 50 = , 52 lb x 20 30 28. 10 = , 9 mi 3 x 1 29. y = x 6 2 20. y = – x 1 11. y = x 26. yes; y = – 1. 5 x 19. y = 2 x 10. y = 5 x 25. no 1 21. y = x 2 5 30. y = – 20 x 3 5 5 -5

Direct Variation ALGEBRA 1 LESSON 5 -5 36 31. y = – x 38. True; a line that is neither horizontal nor vertical can pass through (0, 0) and (– 2, 4). 25 32. y = 6 x 33. y = 9 x 39. False; the line through (0, 3) and (0, 0) is vertical, so it is not a function and is therefore not a direct variation. 1 34. y = – x 32 15 35. y = – x 52 27 36. y = x 64 y 37. a. The ratio is the x same for each pair of values. b. A line through the origin that is neither vertical nor horizontal is the graph of a direct variation. 40. True; for the equation y = kx, if one side is multiplied by 3, then the other side must be multiplied by 3. 41. 5 y = x 2 5 -5
Direct Variation ALGEBRA 1 LESSON 5 -5 44. 42. 49. 8 50. – 6 51. 5 52. 2 5 y = – x 2 5 2 45. a. 1 32 53. a. c = 1. 83 g; yes y = x 1. 83 24 b. c = m or 1 b. b = w 43. c = 0. 07625 m 32 c. Check students’ work. 5 y = – x 2 54. A 46. a. 48 volts b. 0. 75 ohms 55. H 47. 12 57. B 48. – 8 58. C 56. A 5 -5
![Direct Variation ALGEBRA 1 LESSON 5 -5 59. [2] y = kx – 4 Direct Variation ALGEBRA 1 LESSON 5 -5 59. [2] y = kx – 4](https://present5.com/presentation/ecf6fc4c5bd90c479e43a9865e2302c8/image-65.jpg)
Direct Variation ALGEBRA 1 LESSON 5 -5 59. [2] y = kx – 4 = k(– 1) 4 = k y = 4 x [1] correct answer but no work shown 68. n < – 80 60. y = 3 x 71. b > 1 1 61. y = x 3 72. 15, 600 ships > 69. t 3. 04 – 70. v – 5 > – 2 2 62. y = 12 – x 1 63. y = x 6 64. r > – 18 65. c – 1. 8 < – 66. m < – 3 67. a 16. 6 > – 5 -5

Direct Variation ALGEBRA 1 LESSON 5 -5 1. Is each equation a direct variation? If it is, find the constant of variation. a. x + 5 y = 10 no b. 3 y + 8 x = 0 yes; – 8 3 2. Write an equation of the direct variation that includes the point (– 5, – 4). 4 5 y = x 3. For each table, tell whether y varies directly with x. If it does, write an equation for the direct variation. a. x – 1 0 1 2 y 3 0 – 6 – 9 b. yes; y = – 3 x x – 1 0 1 3 5 -5 y – 2 0 2 – 6 no

Describing Number Patterns ALGEBRA 1 LESSON 5 -6 (For help, go to Lessons 1– 2 and 1– 5. ) Evaluate each expression for x = 2, 3, 4. 1. 9 + 3(x – 1) 2. 8 + 7(x – 1) 3. 0. 4 – 3(x – 1) 5. – 7 – 10 6. 1. 5 – 3. 4 Subtract. 4. 8 – (– 6) 5 -6
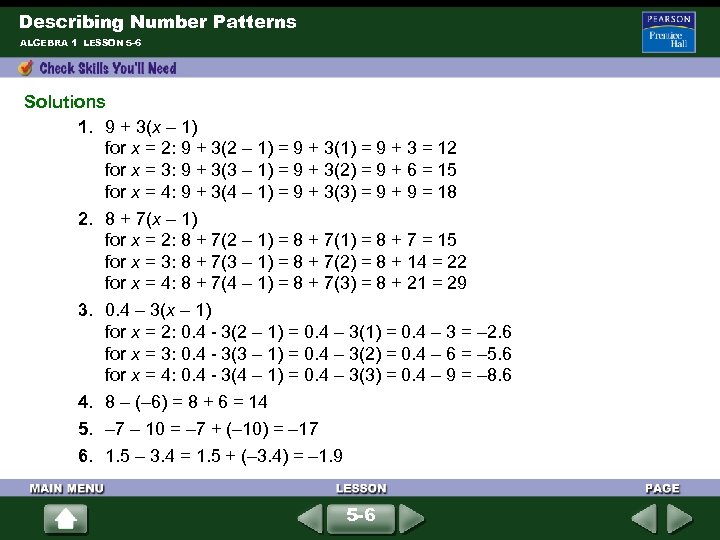
Describing Number Patterns ALGEBRA 1 LESSON 5 -6 Solutions 1. 9 + 3(x – 1) for x = 2: 9 + 3(2 – 1) = 9 + 3(1) = 9 + 3 = 12 for x = 3: 9 + 3(3 – 1) = 9 + 3(2) = 9 + 6 = 15 for x = 4: 9 + 3(4 – 1) = 9 + 3(3) = 9 + 9 = 18 2. 8 + 7(x – 1) for x = 2: 8 + 7(2 – 1) = 8 + 7(1) = 8 + 7 = 15 for x = 3: 8 + 7(3 – 1) = 8 + 7(2) = 8 + 14 = 22 for x = 4: 8 + 7(4 – 1) = 8 + 7(3) = 8 + 21 = 29 3. 0. 4 – 3(x – 1) for x = 2: 0. 4 - 3(2 – 1) = 0. 4 – 3(1) = 0. 4 – 3 = – 2. 6 for x = 3: 0. 4 - 3(3 – 1) = 0. 4 – 3(2) = 0. 4 – 6 = – 5. 6 for x = 4: 0. 4 - 3(4 – 1) = 0. 4 – 3(3) = 0. 4 – 9 = – 8. 6 4. 8 – (– 6) = 8 + 6 = 14 5. – 7 – 10 = – 7 + (– 10) = – 17 6. 1. 5 – 3. 4 = 1. 5 + (– 3. 4) = – 1. 9 5 -6

Describing Number Patterns ALGEBRA 1 LESSON 5 -6 Use inductive reasoning to describe the pattern. Then find the next two numbers in the pattern. a. 1, 9 The pattern is “add 4 to the previous term. ” 5, +4 b. 1, +4 3, 3 To find the next two numbers, you add 4 to each previous term: 9 + 4 = 13 and 13 + 4 = 17. 9 The pattern is “multiply the previous term by 3. ” 3 To find the next two numbers, you multiply each previous term by 3: 9 3 = 27 and 27 3 = 81. c. 1, 9, 25, 49, . . . The pattern is “square of consecutive odd integers. ” To find the next two numbers, square the next two consecutive integers: 92 = 81, 112 = 121. 5 -6
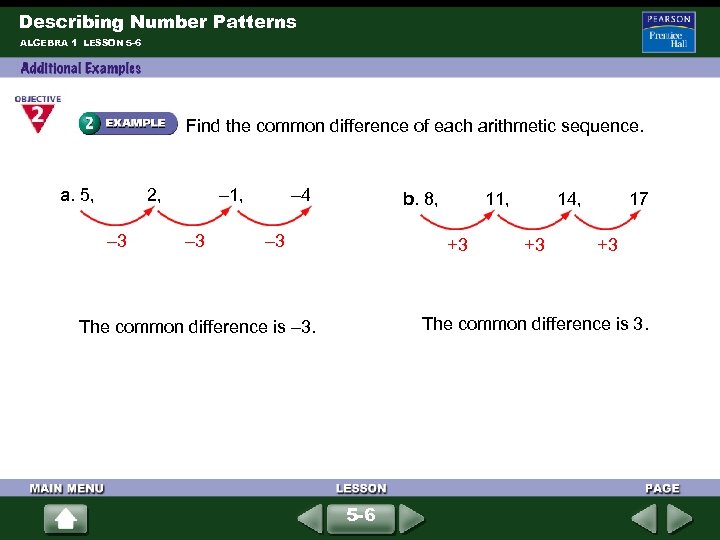
Describing Number Patterns ALGEBRA 1 LESSON 5 -6 Find the common difference of each arithmetic sequence. a. 5, 2, – 3 – 1, – 3 – 4 b. 8, – 3 11, +3 14, +3 17 +3 The common difference is 3. The common difference is – 3. 5 -6

Describing Number Patterns ALGEBRA 1 LESSON 5 -6 Find the first, fifth, and tenth terms of the sequence that has the rule A(n) = 15 + (n – 1)(5). first term: A(1) = 15 + (1 – 1)(5) = 15 + 0(5) = 15 fifth term: A(5) = 15 + (5 – 1)(5) = 15 + 4(5) = 35 tenth term: A(10) = 15 + (10 – 1)(5) = 15 + 9(5) = 60 5 -6

Describing Number Patterns ALGEBRA 1 LESSON 5 -6 pages 270– 273 Exercises 13. 3 1. “Add 2 to the previous term”; 12, 14. 1 2 1 4 3 14. – 4 2. “Multiply the previous term by 1 ”; 20 , 30 . 8 15. – 11 3. “Add 2 to the first term, 3 to the second term and continue, adding 1 more each time”; 18, 24. 4. “Add 0. 04 to the previous term”; 3. 16, 3. 20. 16. 13 5. “Multiply the previous term by 1. 1”; 4. 3923, 4. 83153. 17. – 1 6 18. 0. 8 6. “Add – 2 to the previous term”; – 5, – 7. 19. – 2 7. “Add 1. 1 to the previous term”; 5. 5, 6. 6. 20. 12 8. “Multiply the previous term by 10”; 10, 100. 21. 5 9. “Multiply the previous term by 4”; 512, 2048. 22. 5, 14, 26 1 1 10. “Square the reciprocals of consecutive integers”; , . 25 36 11. “Add – 14 to the previous term”; – 47, – 61. 12. “Multiply the previous term by 5”; 937. 5, 4687. 5. 5 -6 23. – 3, 15, 39 24. – 3, 9, 25

Describing Number Patterns ALGEBRA 1 LESSON 5 -6 25. 17, 44, 80 4 37. , 4 44. 5 min 26. 3. 5, 12. 5, 24. 5 38. 35, 48 27. 2, 23, 51 39. 31, 40 45. Answers may vary. Sample: A(n) = 2 – 4 n 28. 3, – 15, – 39 40. 2. 5, 1. 25 27 81 46. 7 lb 4 oz, 7 lb 9 oz, 7 lb 14 oz, 8 lb 3 oz, 8 lb 8 oz; the baby’s weight at the end of the 4 th week 29. – 7. 1, – 22. 1, – 42. 1 41. 8, 8 1 30. 58, 37, 9 4 4 42. , – 4 27 81 31. 17, 5, – 11 43. a. 32. – 8, – 17, – 29 33. – 0. 8, – 3. 8, – 7. 8 34. – 4, – 10 1 35. 3 , 3 1 4 2 36. 26, 37 b. 47. $4500, $4350, $4200, Answers may vary. $4050, $3900; the balance Sample: Inductive after 4 payments reasoning is making conclusions based on patterns, while deductive reasoning is making conclusions based on given facts. Answers may vary. Check students’ work. 5 -6

Describing Number Patterns ALGEBRA 1 LESSON 5 -6 1 56. 11 , 12, 13 1 48. a. 1 2 4; 7 1 2 ) ) 3 57. 4. 5, – 22. 5 4 2 b. = 2; 8 1 3 58. – 2, – 5. 2, – 11. 6 2 c. When there are more than three terms you can test the pattern to make sure it is reasonable. 49. No; there is no common difference. 3 59. 1, 2 , 5 4 5 5 60. a. 11, 14 b. 50. Yes; the common difference is – 4. 51. No; there is no common difference. 52. No; there is no common difference. 53. Yes; the common difference is – 15. 54. Yes; the common difference is – 0. 8. 55. a. 1, 5, 10, 5, 1 b. 1, 2, 4, 8, 16; 32 c. The points lie on a line. 5 -6

Describing Number Patterns ALGEBRA 1 LESSON 5 -6 61. a. Yes; for each input there is only one output value. b. For every increase of 7 in the key position, the frequency doubles. 66. value of new term = value of previous term + 4 62. a. 21 b. 89 c. Answers may vary. Sample: 3, 3, 6, 9, 15, 24, 39 68. value of new term = value of previous term • (– 2. 5) 63. value of new term = value of previous term + 6 64. value of new term = value of previous term • 1. 5 67. value of new term = value of previous term ÷ 7 69. x; 4 x + 4 70. 3 a + 2 b; 10 a + 7 b + c 71. a. 10 b. – 6 c. A(n) = 10 + (n – 1)(– 6) 65. value of new term = value of previous term – 2. 5 5 -6
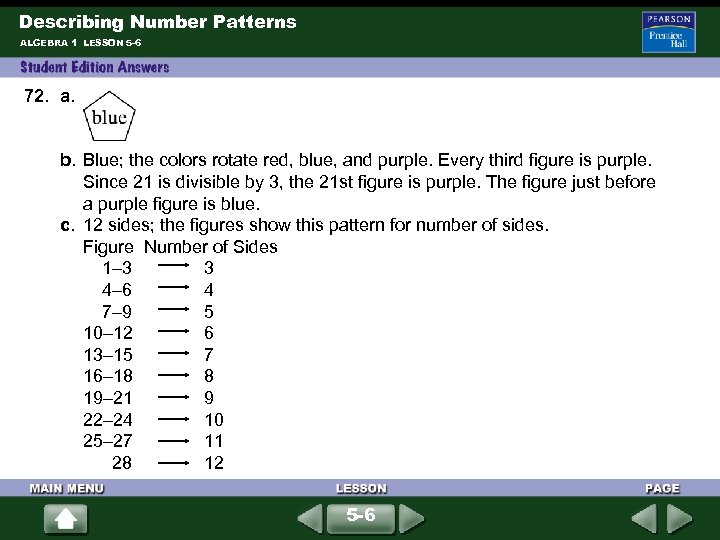
Describing Number Patterns ALGEBRA 1 LESSON 5 -6 72. a. b. Blue; the colors rotate red, blue, and purple. Every third figure is purple. Since 21 is divisible by 3, the 21 st figure is purple. The figure just before a purple figure is blue. c. 12 sides; the figures show this pattern for number of sides. Figure Number of Sides 1– 3 3 4– 6 4 7– 9 5 10– 12 6 13– 15 7 16– 18 8 19– 21 9 22– 24 10 25– 27 11 28 12 5 -6

Describing Number Patterns ALGEBRA 1 LESSON 5 -6 73. a. – 5 b. 6 c. A(n) = – 5 + (n – 1)(6) 77. H 81. [4] a. ƒ(n) = 26, 500 + 2880 n b. 2008 is 7 years after 2001. ƒ(7) = 26, 500 + (2880)(7) = $46, 660 Marta’s 2008 salary is $46, 660. [3] function and salary found but work not shown [2] minor computation error in finding salary [1] function shown but salary not found 78. C 82. y = – x 4 79. H 83. y = 24 x 74. C 75. F 76. A 5 80. [2] The common difference is – 3. 84. y = – 14 x The seventh term is 85. y = 0. 14 x 24 + (7 – 1)(– 3) = 6. 31 86. y = – x 11 [1] explanation incomplete 31 87. y = – x 110 5 -6
Describing Number Patterns ALGEBRA 1 LESSON 5 -6 3 88. y = – x 2 2 89. y = x 3 90. {– 20, – 4, 8} 91. {– 19, – 3, 9} 92. {– 2, 7, 19} 93. {2, 4, 10} 94. {2, 4, 10} 1 1 1 95. {– 6 , – 4 , – 1 } 2 4 4 96. a. about 84% b. about 11% 5 -6

Describing Number Patterns ALGEBRA 1 LESSON 5 -6 1. Use inductive reasoning to describe each pattern. Then find the next two numbers in each pattern. 1 1 1 a. 1, 2. 5, 4, . . . b. , , , . . . 2 4 8 add 1. 5 to the 1 1 1 multiply the previous term by ; , 2 16 32 previous term; 5. 5, 7 2. Find the common difference of each arithmetic sequence. 2 3 1 3 a. – 1, – , 0, . . . 1 3 b. 46, 34, 22, 10, . . . – 12 3. Find the second, sixth, and ninth terms of the sequence that has the rule A(n) = – 3 + (n – 1)(6). 3, 27, 45 4. Is – 2, 3, 8, 10, . . . an arithmetic sequence? Explain. No; the difference between the first two terms is 5, but the difference between the fourth and third terms is 2. 5 -6
Graphs and Functions ALGEBRA 1 CHAPTER 5 1– 2. Answers may vary. Samples: 3. yes; domain: {– 2, 3, 5, 8}; range: {5, 6, 12} 1. 4. no 5. If any vertical line crosses the graph in two or more places, the graph does not represent a function. 6. {5, 9, 14, 41, 69} 7. {– 14, – 5, – 2, 2. 5, 7} 8. 2. 5 -A
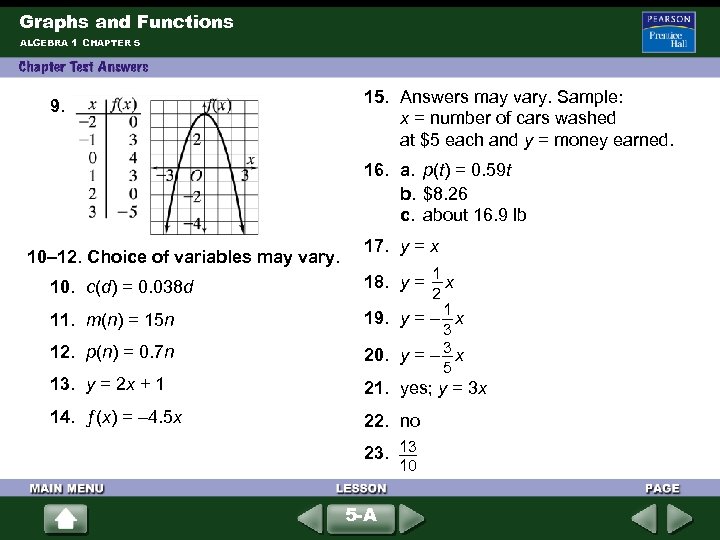
Graphs and Functions ALGEBRA 1 CHAPTER 5 9. 10– 12. Choice of variables may vary. 15. Answers may vary. Sample: x = number of cars washed at $5 each and y = money earned. 16. a. p(t) = 0. 59 t b. $8. 26 c. about 16. 9 lb 17. y = x 10. c(d) = 0. 038 d 1 18. y = x 11. m(n) = 15 n 1 19. y = – x 12. p(n) = 0. 7 n 13. y = 2 x + 1 14. ƒ(x) = – 4. 5 x 2 3 3 20. y = – x 5 21. yes; y = 3 x 22. no 23. 13 10 5 -A

Graphs and Functions ALGEBRA 1 CHAPTER 5 24. 4. 5 25. – 1 26. 150 m. L 27. 5; – 35, – 30, – 25 28. 1; 5. 7, 6. 7, 7. 7 29. – 8 30. 3 31. No; there is no common difference. 32. Yes; the common difference is 0. 25. 33. C(p) = 3 p 5 -A
ecf6fc4c5bd90c479e43a9865e2302c8.ppt