Релаксационные свойства полимерных тел в твердом агрегатном состоянии

Релаксационные свойства полимерных тел в твердом агрегатном состоянии Релаксация - процесс установления ТМД-равновесия в Релаксация - макроскопических физических системах после удаления факторов, выведших ее из этого состояния. Например, релаксация бывает упругая, магнитная, акустическая и др. Лекция 23 2

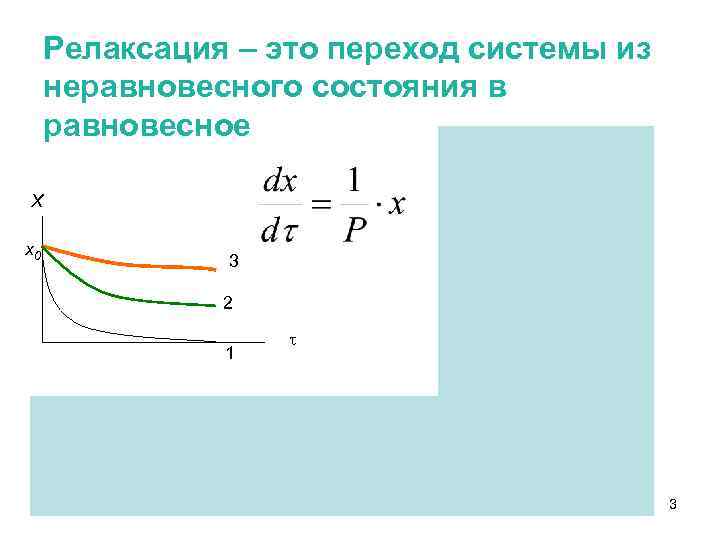Релаксация – это переход системы из неравновесного состояния в равновесное Х х0 3 2 1 х= х0 Лекция 23 – 1 ·е 3

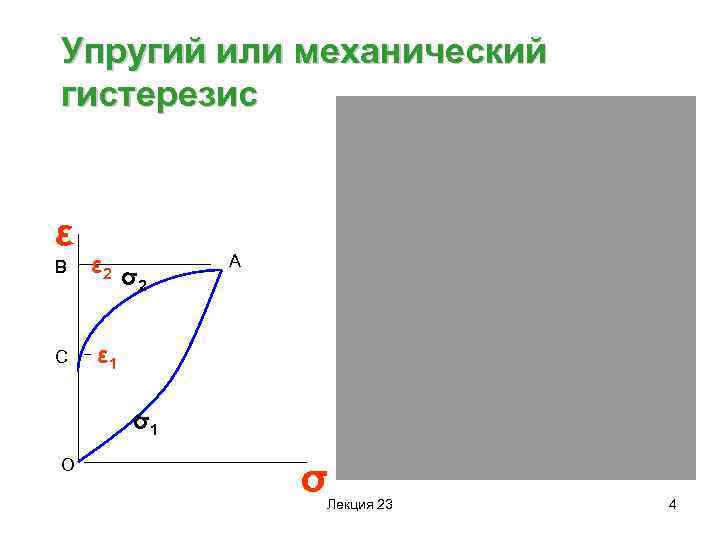Упругий или механический гистерезис ε В С ε 2 σ 2 А ε 1 σ1 О σ Плотность работы, Дж/м 3 Плотность работы Лекция 23 4

Механическая энергия превращается в теплоту ! Тепловыделение активирует химические реакции макромолекул, в частности, реакции окисления атмосферным О 2. Следствие – преждевременное старение изделий (деталей). Лекция 23 5

Механическая работа вызывает реакции окисления и старение изделия из полимера. # Деталь аппарата или изделие надо заменять. # Экономические затраты м. б. велики. # Разработаны методы борьбы со старением полимеров. С ними уже познакомились в конце курса. # Лекция 23 6

РАСТВОРЫ ПОЛИМЕРОВ Общая характеристика полимерных растворов. Набухание. Фазовые диаграммы полимер-растворитель. Критические температуры растворения. Второй вириальный коэффициент. Термодинамическое качество растворителя. Разбавленные растворы полимеров. Гидродинамические свойства макромолекул в растворах. Природа вязкости растворов полимеров. Относительная, приведенная, удельная и характеристическая вязкости полимеров. Связь характеристической вязкости с ММ и среднестатистическими размерами макромолекулярного клубка. -температура. Концентрированные растворы полимеров и гели. Течение растворов и расплавов полимеров. Ньютоновские и неньютоновские жидкости. Релаксационные свойства растворов полимеров. Полиэлектролиты. Свойства растворов полиэлектролитов. Изоэлектрическая и изоионная точки. Лекция 23 7

РАСТВОРЫ ПОЛИМЕРОВ Лекция 23 8

Макромолекулы в разбавленных растворах Важную информацию об индивидуальных изолированных макромолекулах можно получить при изучении разбавленных растворов полимеров при ИХ течении. Таковой информацией являются сведения о конформациях и конфигурациях, размерах и форме макромолекул, молекулярных массах и ММР, о химической микроструктуре, о типе и силе взаимодействий с молекулами растворителей и др. Реальные макромолекулы в растворах имеют большие размеры из-за собственного объема и осмотического набухания , которое имеет место из-за межмолекулярного взаимодействия сегментов с молекулами растворителя. Увеличение размеров макромолекулярных клубков описывают коэффициентом набухания посредством гидродинамического радиуса R или среднеквадратичного расстояния h =( R 2/ R 2 )1/2 = h 2 1/2/ h 2 1/2 Лекция 23 9

Оценка формы и размеров макромолекулы Уравнение Хаггинса уд /с=[ ] + k [ ]с2 +…. Формула Марка-Куна-Хувинка [ ]=К Мa a=0 – компактная сфера, не встречается при растворении макромолекул; a=0. 5 – гауссов клубок в -условиях; a=0. 6 -0. 8 – гибкие макромолекулы в хорошем растворителе; a=1. 0 -1. 5 – протекаемые клубки и жесткие макромолекулы. формула Флори-Фокса [ ] M= h 2 3/2 где – универсальная постоянная (коэффициент Флори), равная 2. 84 · 1021 моль-1 (2. 84 · 1023 моль-1) для гауссовых цепей. Лекция 23 10

Оценка среднеквадратичного расстояния ħ 2 ½ Длина вытянутой ССЦ (L): L=l ·N Среднее расстояние между концами свернутой ССЦ в рамках модели ССЦ: ħ =l ·N½ После объединения формул: L/ ħ=N ½ Это отношение показывает степень свернутости ССЦ, которая увеличивается по мере роста числа сегментов N. Другими словами, это простое выражение показывает, что чем длиннее цепь, тем она сильнее свернута в клубок определенной степени рыхлости. Средние размеры ССЦ ħ ~ не числу n, а корню квадратному из числа сегментов: ħ ~ N 1/2. Число сегментов N, в свою очередь, пропорционально длине вытянутой макромолекулы L. Отсюда следует присущая макромолекулам Лекция 23 принципиально новая количественная ½ 11

Растворы полимеров являются истинными и термодинамически устойчивыми системами. Им присуща обратимость. Они обладают специфическими свойствами, значительно отличающими их от свойств низкомолекулярных растворов. Правило фаз Гиббса для растворов полимеров С – число степеней свободы; К – число компонентов в системе; Ф – число фаз Лекция 23 12

Условные стадии неограниченного растворения полимеров Набухание полимера характеризуется величиной α - степень набухания Лекция 23 13

• Макромолекулярные клубки в разбавленном растворе (стадия VI) пропитаны иммобилизованным растворителем таким образом, что каждое мономерное звено цепи окружено десятками и даже сотнями молекул растворителя, сравнимых по размерам с повторяющимся звеном. Поэтому макромолекула находится в развернутом состоянии. Лекция 23 14

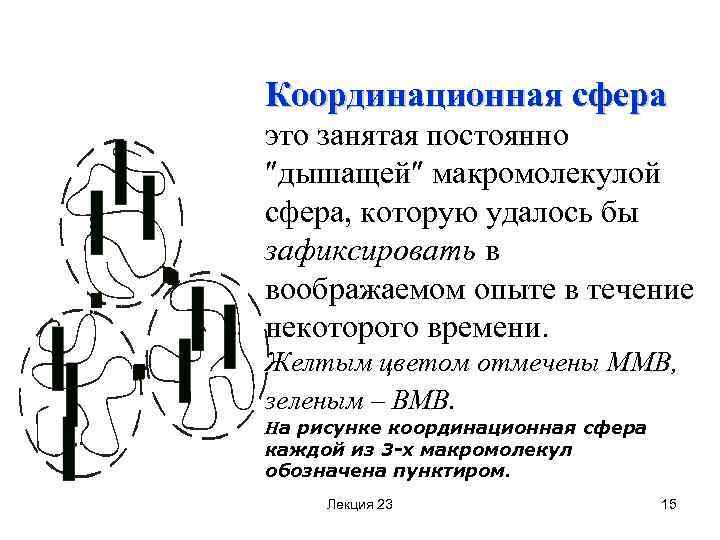Координационная сфера это занятая постоянно дышащей макромолекулой сфера, которую удалось бы зафиксировать в воображаемом опыте в течение некоторого времени. Желтым цветом отмечены ММВ, зеленым – ВМВ. На рисунке координационная сфера каждой из 3 -х макромолекул обозначена пунктиром. Лекция 23 15

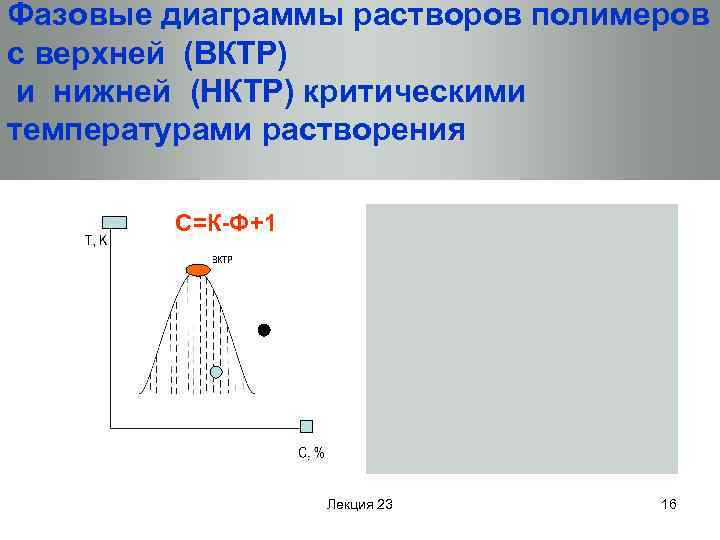Фазовые диаграммы растворов полимеров с верхней (ВКТР) и нижней (НКТР) критическими температурами растворения С=К-Ф+1 Лекция 23 16

Вязкость растворов Вязкость полимеров Вязкость (внутреннее трение) – свойство Вязкость жидких, а также газообразных и твердых тел оказывать сопротивление их течению, т. е. перемещению одного слоя относительно другого под действием внешних сил, таких как гравитационные, например, в вискозиметре. Лекция 23 17

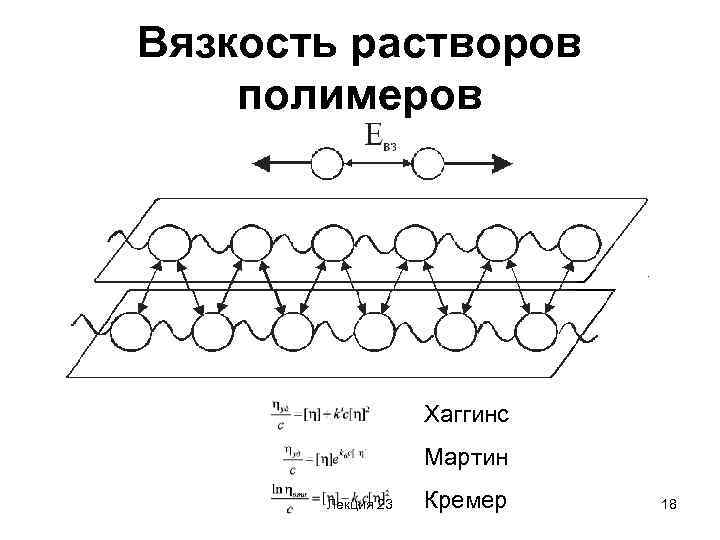Вязкость растворов полимеров Хаггинс Мартин Лекция 23 Кремер 18

Вязкость растворов полимеров как структурно чувствительное свойство уд /с уд =( - о)/ о lim ( уд /с) = [ ] с 0 Уравнение Хаггинса уд /с=[ ] + k [ ]с2 +…. где Ф = 2, 84· 1023 моль-1 – постоянная Флори; М – моляр масса образца; [η] – характеристич вязкость Лекция 23 19

Уравнение Марка – Куна – Хаувинка [η] = К·Mа Графическое определение характеристической вязкости [η] = lim (ηуд/с) с→ 0 К и α – константы уравнения, индивидуальные для каждой конкретной пары полимер-растворитель. Величина α характеризует степень свёрнутости клубка, а К зависит от температуры раствора (в справочниках) Чем в более развернутой конформации находятся клубки, тем бóльшей вязкостью обладают их растворы Лекция 23 20

Понятие исключенного объема Исключенный объем – тот объем, из Типичная форма макромолекулы и той же макромолекулы-клубка с исключенным объемом Глобула в правом нижнем углу. которого данная макромолекула вытесняет все остальные. Исключенный объем является следствием фактического отталкивания макромолекул друг от друга, в результате дальних взаимодействий. Каждая макромолекула в очень разбавленном растворе в хорошем растворителе стремится исключить из объема, который она занимает все другие макромолекулы за счет работы сил отталкивания. Понятие исключенного объема можно связать с понятием набухания , который количественно связан с R и h =(R 2/R 2 )1/2 и Лекция 23 = h 2 1/2/ h 2 1/2 21

Полиэлектролиты Макромолекулы, содержащие в своей структуре способные к диссоциации ионогенные группы, называются полиэлектролитами. Это - кислоты и основания (сильные и слабые), а также самые разные соли Полиамфолиты содержат одновременно кислотные и основные группы. Типичными полиамфолитами являются белки Лекция 23 22

Поликислоты и полиоснования Полиакриловая и полиметакриловая кислоты Поливиниламин Лекция 23 23

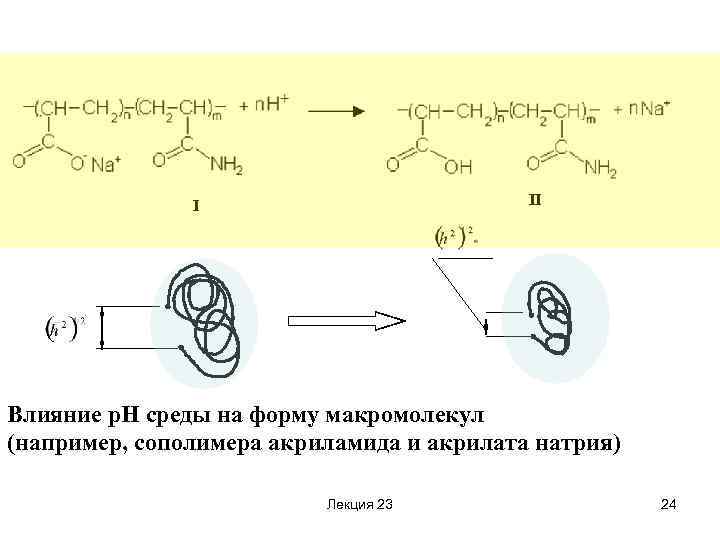II I Влияние р. Н среды на форму макромолекул (например, сополимера акриламида и акрилата натрия) Лекция 23 24

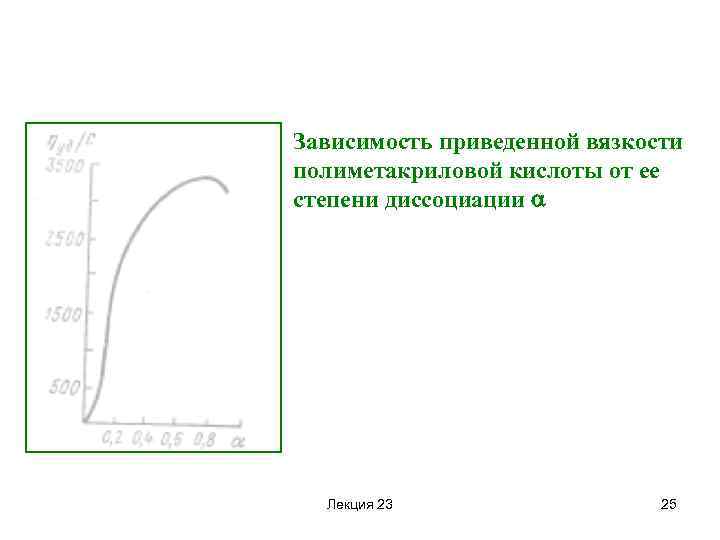Зависимость приведенной вязкости полиметакриловой кислоты от ее степени диссоциации Лекция 23 25

Концентрированные растворы полимеров • Полимерные растворы в зависимости от величины произведения [η]·с относят к • а) разбавленными ([η]·с < 1); или к • б) концентрированными ([η]·с > 1) Со свойствами разбавленных растворов уже познакомились Два явления характерны для концентрированных растворов: 1. Гистерезис вязкости 2. Пластификация полимеров Лекция 23 26

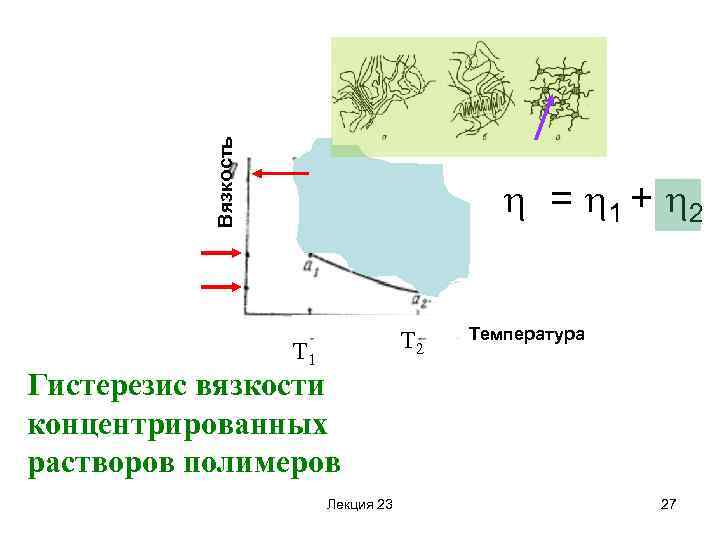Вязкость = 1 + 2 Т 1 Температура Гистерезис вязкости концентрированных растворов полимеров Лекция 23 27

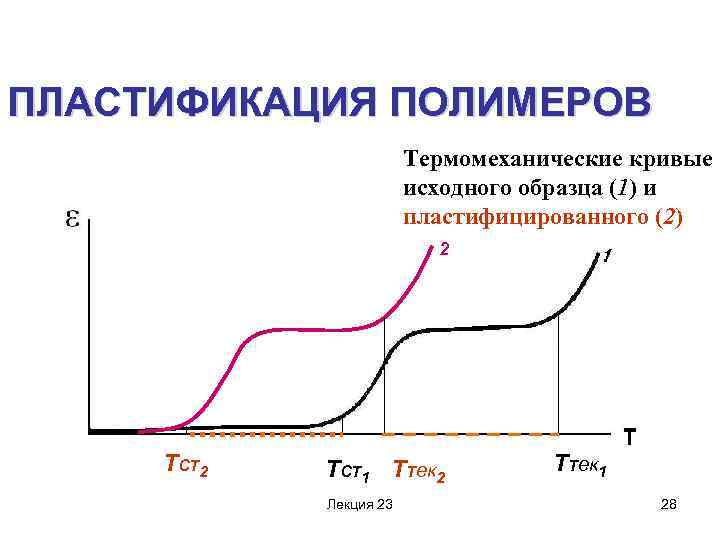ПЛАСТИФИКАЦИЯ ПОЛИМЕРОВ Термомеханические кривые исходного образца (1) и пластифицированного (2) 2 ТСТ 1 ТТек 2 Лекция 23 ТТек 1 28

ЗАЧЕТ по курсу ХИМИЯ и ФИЗИКА ПОЛИМЕРОВ (основы физической химии полимеров) Пример Фамилия И. О. _________ Группа______ Дата_______ Оценка______ 1. Гибкость как особенное свойство структурных единиц химического вещества. Количественные характеристики гибкости. Модель ССЦ. 2. Фракционирование полимеров. Физикохимические основы фракционирования. Лекция 23 29