Рекурсия У попа была собака он


Рекурсия У попа была собака он ее любил. Она съела кусок мяса - он ее убил. В землю закопал, на могиле написал: . . . Не стоит даже спрашивать о том, знаете ли Вы эти строки. Конечно, знаете. И быть может приведете подобный пример. Но знаете ли Вы, что именно эти детские смешные строчки приоткроют нам дверь в очень интересный раздел информатики - рекурсивное программирование.

Рекурсия Перед вами примеры рекурсии в естественном языке: Человек, которого лошадь, проигравшая забег, сбросила, не пострадал. Картина, повешенная человеком, которого женщина, живущая рядом, наняла, упала. Пример рекурсии в литературном творчестве: Вот дом, Котрый построил Джек. А это пшеница, Которая в темном чулане хранится В доме, Который построил Джек. . . Но перед тем, как дать определение термину рекурсия, обратимся к творчеству художника Пита Мондриана, жившему в Нидерландах(1872 – 1944):

Рекурсия Пример рекурсии в изобразительном искусстве: Пит Мондриан Процедура Мондриан (пр-к) Если пр-к имеет размеры, слишком большие для вашего Нидерланды восприятия То (разделить пр-к на два (1872 – 1944) меньших) Мондриан (первый из полученных меньших пр-ков) Мондриан (второй из полученных меньших пр-ков) Конец процедуры Мондриан

Рекурсия А теперь давайте обратимся к исполнителю Кукарача: Кукарача — это исполнитель, который может ползать по клетчатому полю и толкать перед собой кубики. Задача. Где-то под Кукарачей, в том же столбце расположен кубик с символом. Написать программу, по которой исполнитель толкнет кубик вниз и вернется в исходное положение. Решение. ЭТО поиск ВНИЗ Вам понятно, ЕСЛИ ПУСТО ТО поиск как работает эта ВВЕРХ короткая КОНЕЦ программа?

Рекурсия — это такой способ организации вспомогательного алгоритма (подпрограммы), при котором эта подпрограмма (процедура или функция) в ходе выполнения ее операторов обращается сама к себе. Вообще, рекурсивным называется любой объект, который частично определяется через себя.

Рекурсия Обращение к рекурсивной подпрограмме ничем не отличается от вызова любой другой подпрограммы. При этом при каждом новом рекурсивном обращении в памяти создаётся новая копия подпрограммы со всеми локальными переменными. Такие копии будут порождаться до выхода на граничное условие. Очевидно, в случае отсутствия граничного условия, неограниченный рост числа таких копий приведёт к аварийному завершению программы за счёт переполнения стека. Давайте вернемся к стихам о собаке и поставим граничное условие для предотвращения зацикливания программы.

Рекурсия АЛГ О_СОБАКЕ (АРГ ЦЕЛ Н) НАЧ ЕСЛИ Н>0 ТО ВЫВОД НС, “ КАК ЭТО БЫЛО: ” ВЫВОД НС, “ У ПОПА БЫЛА СОБАКА – ОН ЕЕ ЛЮБИЛ. ” ВЫВОД НС, “ОНА СЪЕЛА КУСОК МЯСА – ОН ЕЕ УБИЛ. ” ВЫВОД НС, “УБИЛ И ЗАКОПАЛ И НА МОГИЛЕ НАПИСАЛ: ” О_СОБАКЕ (Н-1) ВСЕ КОН

Рекурсия Порождение все новых копий рекурсивной подпрограммы до выхода на граничное условие называется рекурсивным спуском. Максимальное количество копий рекурсивной подпрограммы, которое одновренно может находиться в памяти компьютера, называется глубиной рекурсии. Завершение работы рекурсивных подпрограмм, вплоть до самой первой, инициировавшей рекурсивные вызовы, называется рекурсивным подъёмом. Выполнение действий в рекурсивной подпрограмме может быть организовано одним из вариантов: алг Р нач нач P операторы P кон операторы рекурсивный подъём рекурсивный спуск кон и рекурсивный спуск, и рекурсивный подъём

Рекурсия Пример 1. Классический пример, без которого не обходятся ни в одном рассказе о рекурсии, — определение факториала. С одной стороны, факториал определяется так: n!=1*2*3*. . . *n. С другой стороны, Граничным условием в данном случае является n<=1. АЛГ ЦЕЛ ФАКТОРИАЛ(АРГ ЦЕЛ Н) Function Factorial(N: integer): Extended; НАЧ ЕСЛИ Н<=1 Begin ТО ЗНАЧ: =1 If N<=1 Then Factorial: =1 ИНАЧЕ ЗНАЧ : = Н * ФАКТОРИАЛ (Н-1) Else Factorial: =Factorial(N-1)*N ВСЕ End; КОН

Рекурсия Пример 2. Определим функцию K(n), которая возвращает количество цифр в заданном натуральном числе n: Procedure K(N: Longint; Var Kol: Byte); Begin If N<10 Then Kol: =1 Else Begin K(N Div 10, Kol); Kol: =Kol+1 End;

Рекурсия Пример 3. Вычислить сумму элементов линейного массива. При решении задачи используем следующее соображение: сумма равна нулю, если количество элементов равно нулю, и сумме всех предыдущих элементов плюс последний, если количество элементов не равно нулю. {Рекурсивная функция} Function Summa(N : Byte; A: Lin. Mas) : Integer; Begin If N = 0 Then Summa : = 0 Else Summa : = A[N] + Summa(N - 1, A) End;
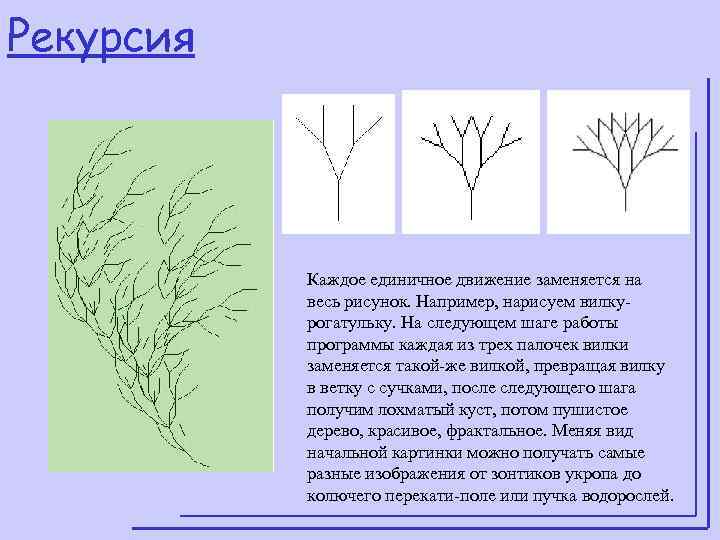
Рекурсия Каждое единичное движение заменяется на весь рисунок. Например, нарисуем вилку- рогатульку. На следующем шаге работы программы каждая из трех палочек вилки заменяется такой-же вилкой, превращая вилку в ветку с сучками, после следующего шага получим лохматый куст, потом пушистое дерево, красивое, фрактальное. Меняя вид начальной картинки можно получать самые разные изображения от зонтиков укропа до колючего перекати-поле или пучка водорослей.
Рекурсия Желающих получить больше информации об этих удивительных деревьях приглашаем посетить лучшую в Рунете речку, протекающую по самым приятным областям занимательного программирования - фракталам, паутине и, конечно, L-деревьям. Там вы найдете алгоритм построения объемного дерева с возможностью просмотра его стереоизображения и рассуждения о толщине веток. С ссылкой на самого Леонардо да Винчи Речка предполагает, что суммарная площадь сечения всех веток и ствола на любой высоте постоянна, поэтому видимая ширина ствола и веток уменьшается пропорционально квадратному корню из числа веток. Не правда ли красивая идея?
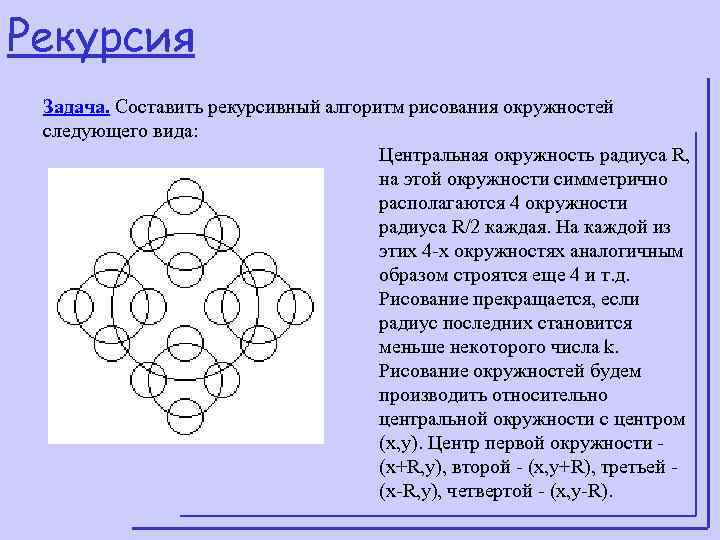
Рекурсия Задача. Составить рекурсивный алгоритм рисования окружностей следующего вида: Центральная окружность радиуса R, на этой окружности симметрично располагаются 4 окружности радиуса R/2 каждая. На каждой из этих 4 -х окружностях аналогичным образом строятся еще 4 и т. д. Рисование прекращается, если радиус последних становится меньше некоторого числа k. Рисование окружностей будем производить относительно центральной окружности с центром (x, y). Центр первой окружности - (x+R, y), второй - (x, y+R), третьей - (x-R, y), четвертой - (x, y-R).

Рекурсия Решение: uses crt, graph; var gd, gm : integer; ch : char; procedure krug(x, y, r : integer); begin Граничное условие! Подставляя вместо k if r>k then различные числа, получаем различное число рекурсивных begin вызовов krug(x+r, y, r div 2); krug(x, y+r, r div 2); krug(x-r, y, r div 2); krug(x, y-r, r div 2); end; circle(x, y, r); end;
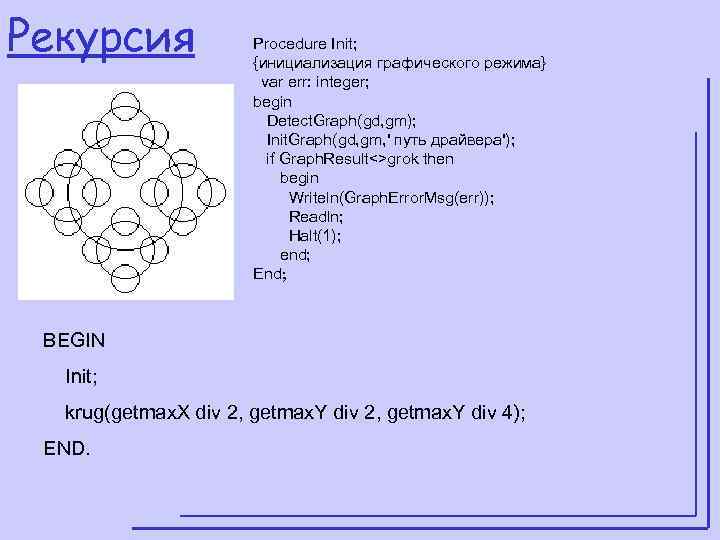
Рекурсия Procedure Init; {инициализация графического режима} var err: integer; begin Detect. Graph(gd, gm); Init. Graph(gd, gm, ' путь драйвера'); if Graph. Result<>grok then begin Writeln(Graph. Error. Msg(err)); Readln; Halt(1); end; End; BEGIN Init; krug(getmax. X div 2, getmax. Y div 4); END.
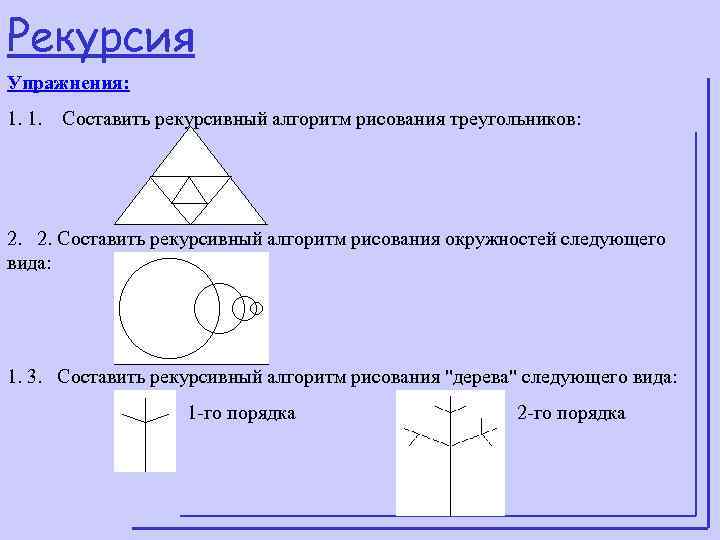
Рекурсия Упражнения: 1. 1. Составить рекурсивный алгоритм рисования треугольников: 2. Составить рекурсивный алгоритм рисования окружностей следующего вида: 1. 3. Составить рекурсивный алгоритм рисования "дерева" следующего вида: 1 -го порядка 2 -го порядка
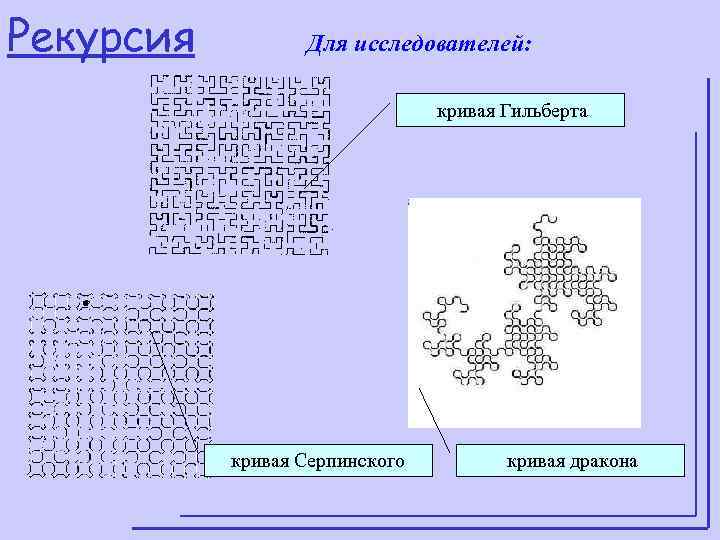
Рекурсия Для исследователей: кривая Гильберта кривая Серпинского кривая дракона

Рекурсия На портале Ферагана. ru на сайте замечательного Арбузника были найдены прекрасные картины: авторы Евгений Скляревский, Максим Меметов А у Шестакова А. П. , 2001 г. , были найдены удачные определения и задачи http: //comp-science. narod. ru/ В презентацию включена программа демонстрации трехмерных фракталов из статьи А. Лукичева "Обзор "Фракталы в Интернет" в журнале "Компьютерные инструменты в образовании" N 5, 2001 http: //fractal. nsu. ru Спасибо всем! Садовая Ирина Владимировна gimn 10 tver@mail. ru

