metabolic_control.ppt
- Количество слайдов: 57

Регуляция метаболизма Михаил Пантелеев

Что такое биологическая сложность? www. cartage. org. lb
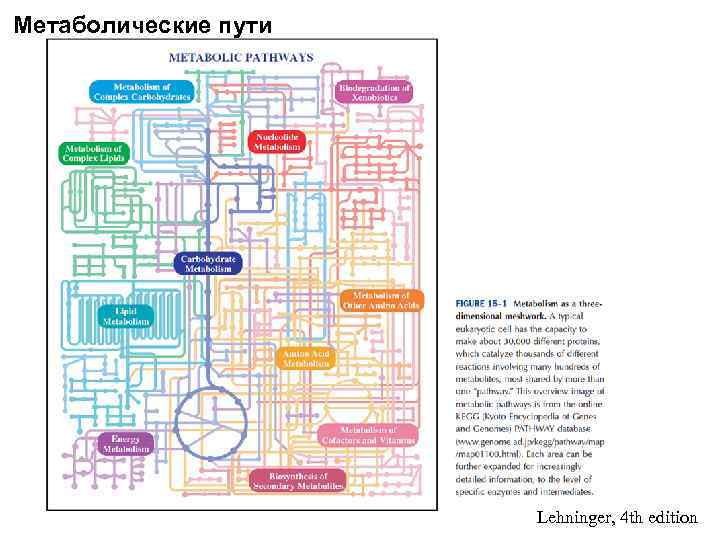
Метаболические пути Lehninger, 4 th edition

Основные типы сложных систем 1. Метаболические 2. Внутриклеточная сигнализация 3. Сигнализация, защита, морфогенез в больших клетках и тканях 4. Экспрессия генов

Типичные вопросы 1. Что можно считать системой? 2. Как выделить системы и подсистемы из десятков тысяч реакций, происходящих в клетке? 3. Если мы знаем только часть системы – что мы можем сказать о неизвестных нам реакциях? 4. Как быть, если мы плохо знаем параметры системы? 5. Как на основании устройства предсказать поведение системы? В каких состояниях может она работать? 6. Какие элементы системы являются регулирующими? Как она реагирует на возмущения и модификации? 7. Как система может обеспечивать постоянство работы при меняющихся внешних условиях?

Плохие особенности 1. Высокая сложность биологических систем: много компонентов, много реакций, сложность отдельных компонентов, наличие транспортных процессов, комбинаторная сложность 2. Плохая изученность биологических систем: даже в самых изученных системах могут быть разбросы на порядки в значениях параметров; в общем же случае огромные куски системы могут быть совершенно неизвестны.

Хорошие особенности 1. Осмысленность биологических систем: они не случайны, сформировались в процессе длительного отбора и выполняют физиологические функции. Благодаря этому они обладают такими качествами как модульность, грубость, часто стационарность и т. п.

Часть первая Анализ метаболического контроля

Анализ метаболического контроля (MCA – Metabolic Control Analysis) 1963 Higgins – первые работы по полиферментным системам 1965 -1980 Сельков – нелинейные модели регуляции метаболизма, методы редукции и анализа, принципы стабилизации 1973 -74 Kacser&Burns, Heinrich&Rapoport – основы АМК, первые теоремы 1984 Официальное согласование АМК 1989 Acerenza et al. – обобщение АМК на зависящие от времени системы 2003 Peletier et al – обобщение АМК на реакционно-диффузные системы

С чего начинается метаболизм? S 1 E S 2

Основные допущения E 1 E 2 S 1 S 2 S 3 E 3 1. Все реакции изучаемой системы связаны между собой посредством метаболитов 2. Система находится в устойчивом стационарном состоянии 3. Метаболиты и ферменты гомогенно распределены в пространстве 4. Концентрации ферментов являются параметрами, а не переменными 5. Скорости работы ферментов пропорциональны их концентрациям, один фермент влияет на одну реакцию

Кинетика Михаэлиса S 1 E S 2

Эластичность
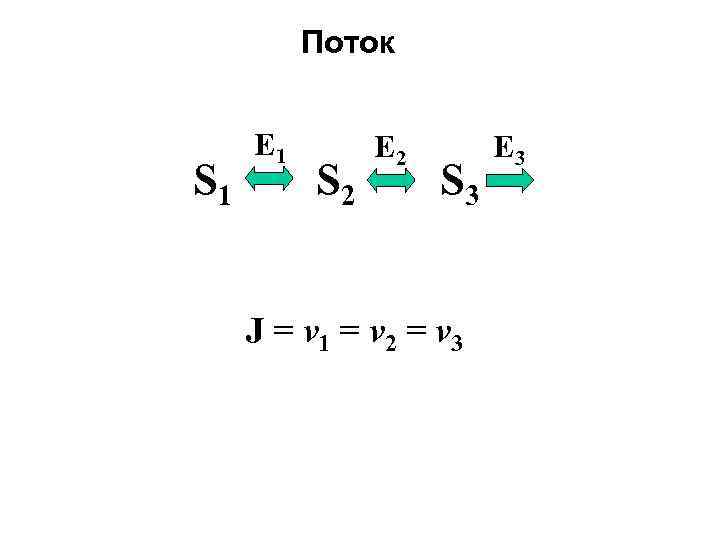
Поток S 1 E 1 S 2 E 2 S 3 J = v 1 = v 2 = v 3 E 3
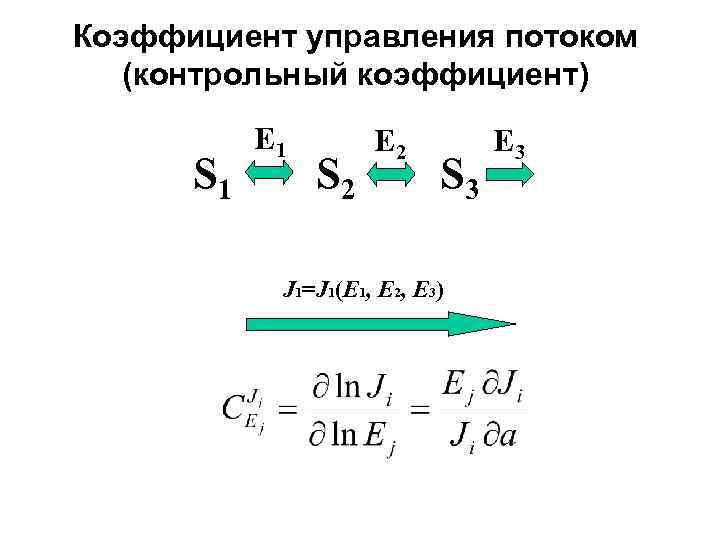
Коэффициент управления потоком (контрольный коэффициент) S 1 E 1 S 2 E 2 S 3 J 1=J 1(E 1, E 2, E 3) E 3

Система в состоянии равновесия +1 V i max /K m. Si (Si – K i. Si+1) v i = (1 + S i/K m. Si + S i+1/K m. Si+1 ) J = v 1 = v 2 = …. . Пусть J = 0, тогда Si – Ki. Si+1 = 0 Si/Si+1=Ki

Отношение концентрации субстрата к концентрации продукта в каждой реакции цепи тем ближе к константе равновесия реакции, чем больше отношение максимальной скорости данной реакции к потоку в цепи S 1 E 1 S 2 E 2 S 3 E 3

Скорость потока в цепи реакций Какая реакция лимитирует поток? определяется «узким местом» реакцией с наименьшей активностью v 1 v 2 v 3 S 1 S 2 S 3 S 1 - константа v i = e i (Si – K i. Si+1) где ei Ki – эффективная константа i-й реакции – константа равновесия
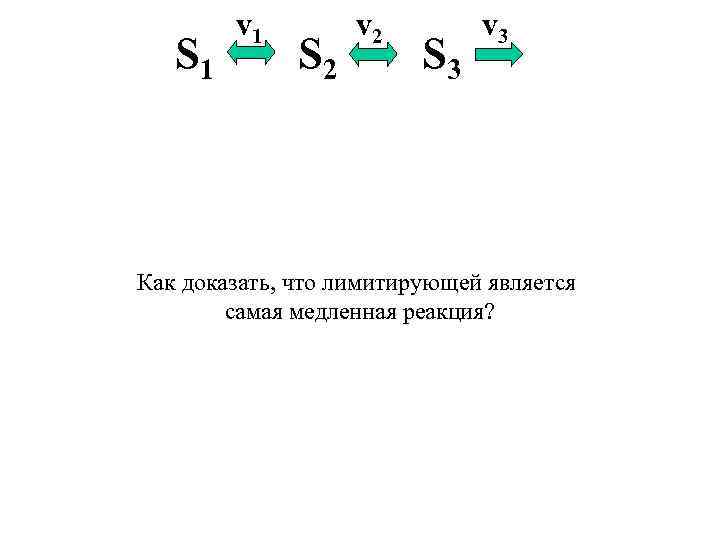
S 1 v 1 S 2 v 2 S 3 v 3 e 1 (S 1 – K 1 S 2) = e 2(S 2 -K 2 S 3) = e 3 S 3 = e 2 S 2/(e 3+e 2 K 2) S 2 = S 1(e 1 e 3+e 1 e 2 K 2)/(e 1 e 3 K 1+e 1 e 2 K 1 K 2+e 2 e 3)= Как доказать, что лимитирующей является =S 1(1+e 2 Kсамая)/(K 1+K 1 реакция? 3 +e 2/e 1) 2/e 3 медленная K 2 e 2/e e 2<<e 1, e 3 => S 2 = S 1/K 1; S 3 = (S 1/K 1)e 2/e 3 J = v 3 = e 2 S 1/K 1 = e 2 S 2 = v 2

Контрольные коэффициенты CJjek = (ek/Jj) (d. Jj/dek) = dln. Jj/dlnek J = v 3 = e 2 S 1/K 1 = e 2 S 2 Ce 1 = (e 1 K 1/e 2 S 1)d. J/de 1= 0, Ce 2 = (e 2 K 1/e 2 S 1)d. J/de 2= А какие будут контрольные коэффициенты = (e 2 K 1 и быстрых /K 1) = для медленных/e 2 S 1)(S 1 реакций? 1, Ce 3= (e 3 K 1/e 2 S 1) d. J/de 3 = 0 CJjk = 1
Насколько важны контролирующие реакции? S 1 E 1 S 2 E 2 S 3 E 2 E 3 S 3
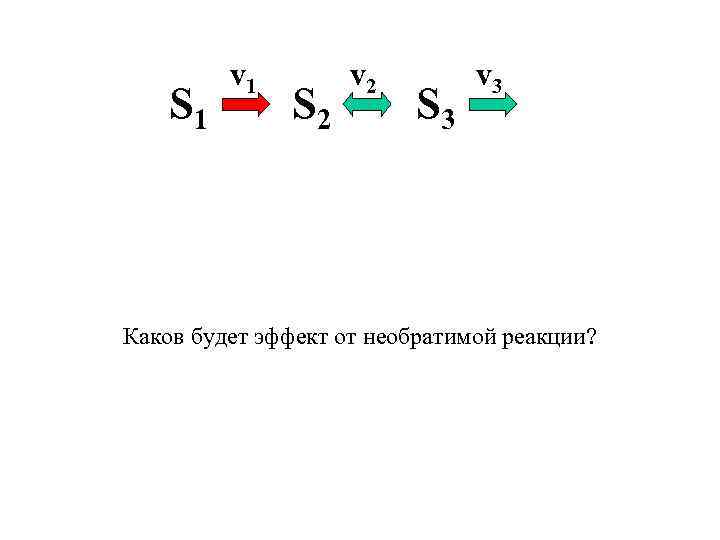
S 1 v 1 S 2 v 2 S 3 v 3 e 1 S 1 = e 2(S 2 -K 2 S 3) = e 3 S 3 J от необратимой реакции? Каков будет эффект= e 1 S 1 Необратимые реакции определяют скорость потока ниже

Контрольные коэффициенты для необратимой реакции CJjek = (ek/Jj) (d. Jj/dek) = dln. Jj/dlnek J = e 1 S 1 Ce 1 = (e 1/e 1 S 1)d. J/de 1= (1/S 1)S 1 = 1, Ce 2 = (e 2/e 1 S 1)d. J/de 2 = 0, Ce 3 = (e 3/e 1 S 1)d. J/de 3 = 0 CJjk = 1

Сочетание необратимости и малой скорости Сочетание двух необратимостей S 1 E 1 S 2 E 2 S 3 E 3

Концентрационные контрольные коэффициенты: CSjek = ek/Sj (d. Sj/dek) = dln. Sj/dlnek Где CJiek - контрольный коэффициент ek - концентрация фермента в k-ой реакции Sj - концентрация j-ого метаболита

Теоремы суммирования: • Ферменты конкурируют в управлении потоком CJjk = 1 • Некоторые ферменты увеличивают, а другие уменьшают концентрацию метаболита CSjk = 0

Теоремы связности: • Ферменты, нечувствительные к воздействиям метаболитов вносят наибольший вклад в управление потоком

Недостатки АМК: 1. Применим только к стационарным системам 2. Работает только вблизи стационара 3. Не может помочь в случае наличия нескольких стационаров или при потере стационара (легко встречающейся в задачках биоинженерии) 4. Требует наличия детальной информации о системе: метаболиты, ферменты, реакции, константы

Часть вторая В поисках стационарного состояния
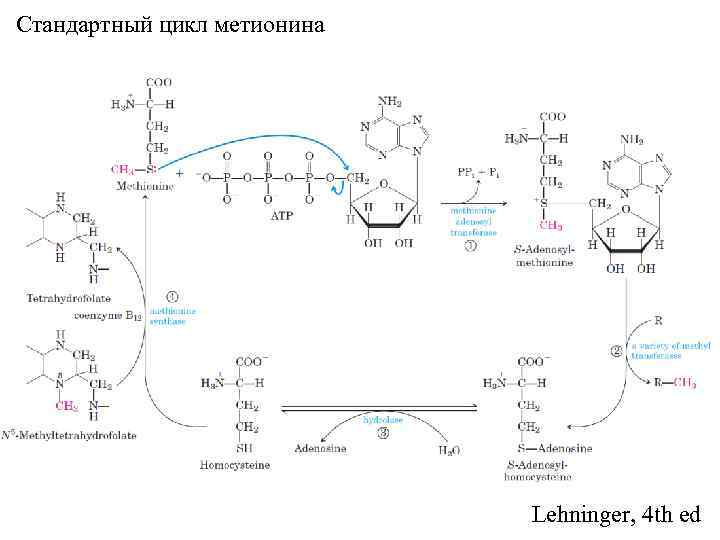
Стандартный цикл метионина Lehninger, 4 th ed


The metabolic aims of Methionine network: 1. To supply the methylases with Ado. Met, the substrate for methylation. 2. To stabilize the blood level of methionine (methionine homeostasis). 3. To participate in redox stress compensation. There is a contradiction between aim 1 and the other two aims, because aim 1 requires the activity of negative feedbacks, while other aims are based on positive feedback loops. This contradiction can be solved by the bi-stable dynamic structure of this network



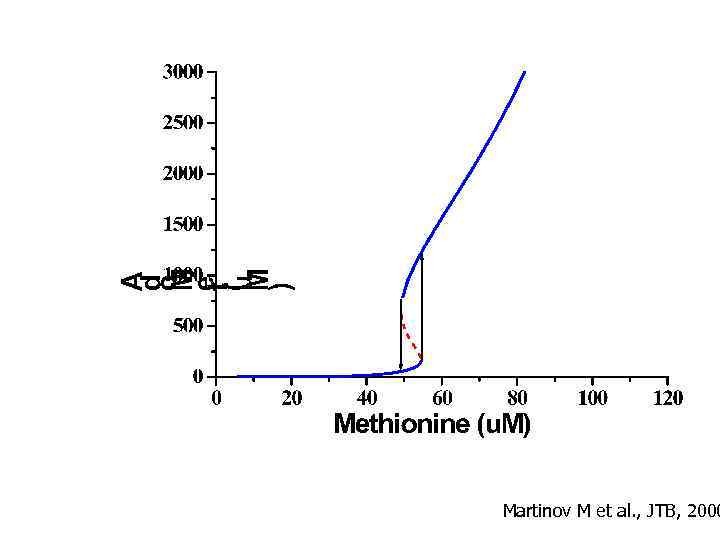
Martinov M et al. , JTB, 2000

Часть третья Расширения АМК

Обобщение ТМК для нестационарных случаев

Обобщение ТМК для гетерогенных случаев
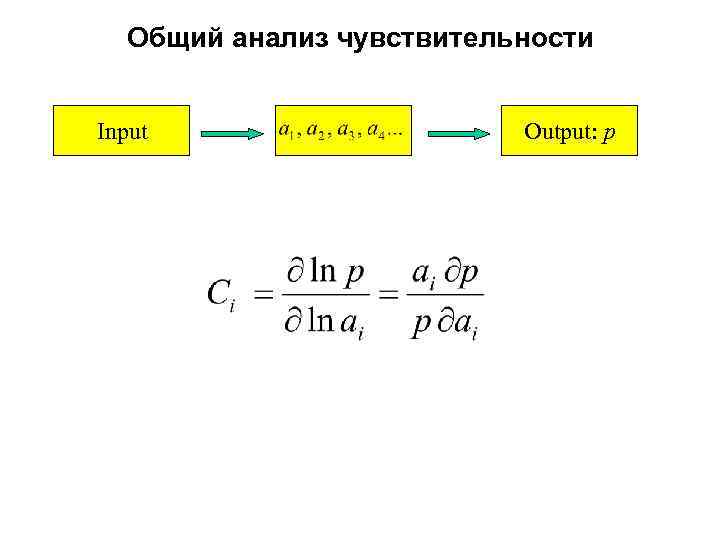
Общий анализ чувствительности Input Output: p

Часть четвертая А если константы реакций неизвестны?

Теория биохимических систем 1969: Savageau vi-1 vi Si vj • Metabolic control analysis: d. Si/dt = vi-1 – vi – vj • Biochemical system theory: d. Si/dt = ui+ – ui-

Biochemical system theory: d. Si/dt = vi-1 – vi – vj gij hij d. Si/dt = ui+ – ui- = ai Sj - bi Sj j j Steady-state: d. Si/dt = 0 = > ui+ – ui- = > ln ai + gij ln Sj = ln bi + hij ln Sj

Стехиометрический анализ E 1 E 2 S 1 S 2 S 3 E 3 Метаболическую сеть можно представить матрицей:
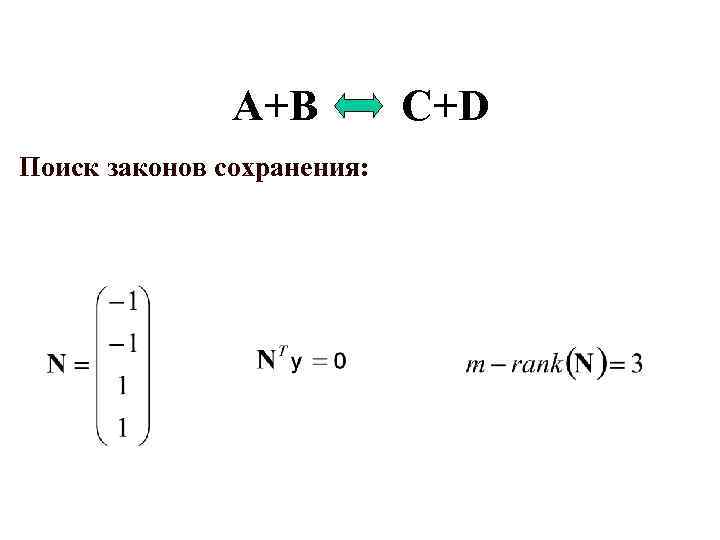
A+B Поиск законов сохранения: C+D


Возможности СА: 1. 2. 3. 4. 5. 6. 7. 8. Поиск законов сохранения Согласованность системы Выделение функциональных путей Потенциальная продуктивность Важность отдельных реакций Выявление групп реакций с общей регуляцией Влияние добавления и удаления реакций Грубость и чувствительность системы

Часть пятая А если сами реакции неизвестны?

Теорема Байеса где P(A) — априорная вероятность гипотезы A P(A | B) — вероятность гипотезы A при наступлении события B (апостериорная вероятность); P(B | A) — вероятность наступления события B при истинности гипотезы A; P(B) — вероятность наступления события B

10 печений 30 конфет ? 20 печений 20 конфет


Часть шестая Системная биология

Классификация подходов в системной биологии: по задаче 1. Causal approaches (анализ известных систем) 2. Probabilistic approaches (реконструкция неизвестных систем)
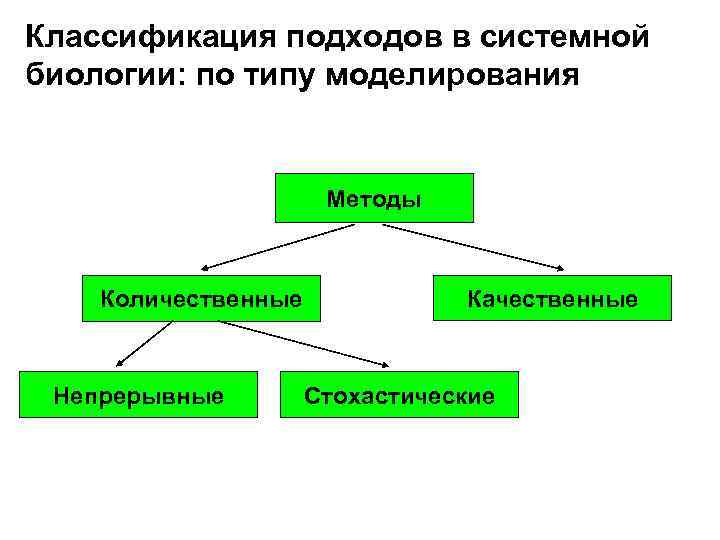
Классификация подходов в системной биологии: по типу моделирования Методы Количественные Непрерывные Качественные Стохастические

Примеры типов систем 1. Метаболические (гомогенные, стационарные) 2. Внутриклеточная сигнализация (гомогенные нестационарные) 3. Сигнализация в больших клетках и тканях (неоднородные и нестационарные) 4. Экспрессия генов (стохастические)

Этапы в изучении системы 1. Реконструирование (неизвестно даже точное устройство) 2. Качественный анализ (устройство известно, но неизвестны параметры) 3. Количественный анализ (все компоненты и константы известны)

Выбор метода в зависимости от изученности Реконструкция Стехиометрический анализ ДУ Теория биохимических систем Анализ метаболического контроля Редукция с использованием теоремы Тихонова Метод регуляторных характеристик Методы модульной декомпозиции
metabolic_control.ppt