Регрессионный анализ Виды зависимостей между переменными 1

Регрессионный анализ

Виды зависимостей между переменными 1. Функциональные: Y = f(X). Имеют место при исследовании связей между неслучайными переменными. Такие связи в эконометрике не рассматриваются. 2. Статистические: изменение одной из величин влечет изменение закона распределения другой (доход – потребление, цена – спрос и т. д. ).

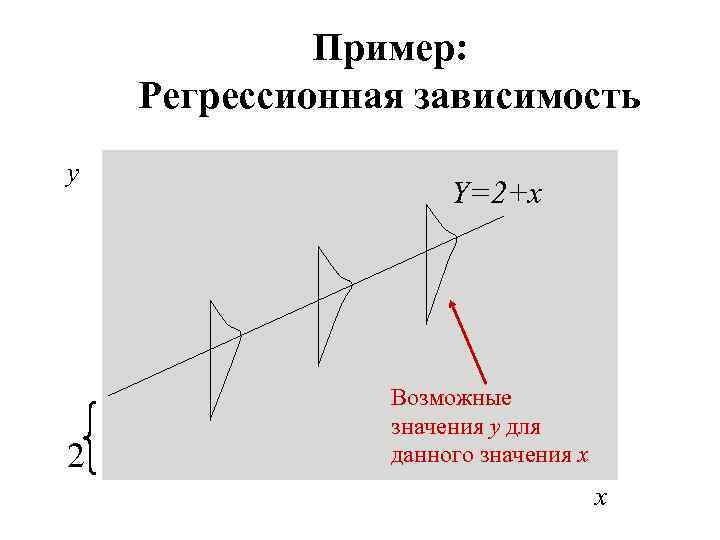Пример: Регрессионная зависимость y 2 Y=2+x Возможные значения y для данного значения x x

Что такое регрессионный анализ? • Регрессионный анализ – наиболее часто используемый инструмент при моделировании. • Регрессионный анализ представляет собой анализ форм связи, устанавливающих количественные соотношения между случайными величинами изучаемого случайного процесса.

Определение регрессии Регрессия – функциональная зависимость между объясняющими переменными и условным математическим ожиданием (средним значением) зависимой переменной, которая строится с целью прогнозирования этого среднего значения при фиксированных значениях объясняющих переменных.

Регрессионный анализ • Поиск вида математического уравнения зависимости выхода от входа системы составляет задачу регрессионного анализа или теории регрессии. Регрессионный анализ позволяет определить теоретическую линию регрессии, то есть осуществить выбор типа регрессионной кривой и расчет ее параметров. • Полученное во время регрессионного анализа уравнение есть экспериментально – статистическая модель исследуемой системы, которая позволит осуществить оптимизацию системы в заданном диапазоне значений аргумента Х, прогнозировать значение ее в этом диапазоне.

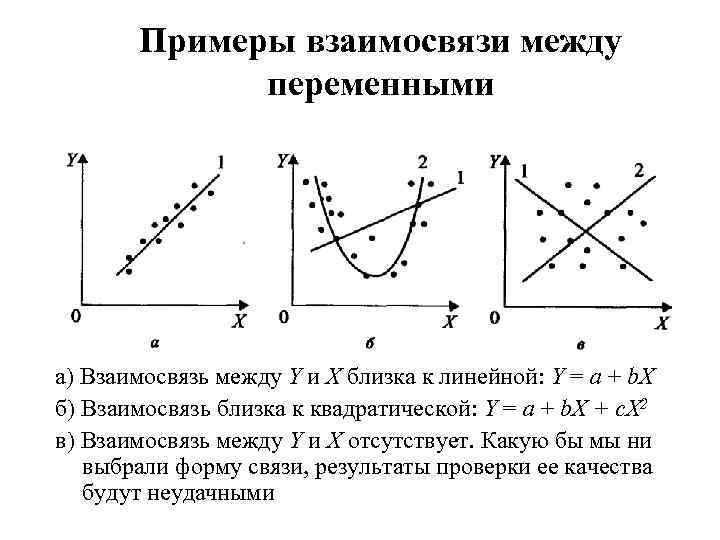Примеры взаимосвязи между переменными а) Взаимосвязь между Y и X близка к линейной: Y = a + b. X б) Взаимосвязь близка к квадратической: Y = a + b. X + c. X 2 в) Взаимосвязь между Y и X отсутствует. Какую бы мы ни выбрали форму связи, результаты проверки ее качества будут неудачными

Регрессионный анализ базируется на таких предпосылках: • ·входные переменные могут иметь произвольную частоту распределения, но для каждого фиксированного значения этих переменных исходная случайная величина имеет нормальную частоту распределения. Это равносильно требованию одномерного нормального распределения. • дисперсия не зависит от математического ожидания М{у}, то есть она не будет отличаться при повторных наблюдениях для какого-нибудь набора значений входных переменных Х. · входные переменные измеряются с малой ошибкой по сравнению с ошибкой исходной переменной.

Эмпирическое уравнение регрессии По выборке ограниченного объема нельзя точно определить теоретические значения 0 и 1. . Можно лишь построить эмпирическое уравнение регрессии: где b 0 и b 1 – оценки параметров 0 и 1 эмпирические коэффициенты регрессии). – оценка условного м. о. M[Y/X = xi].

Метод наименьших квадратов • Нахождение в пределах корреляционного поля кривой, которая бы из всех возможных кривых проходила как можно ближе к точкам данного корреляционного поля, осуществляют с помощью метода наименьших квадратов, которому отвечает следующее правило, • где yi – экспериментальное значение выхода; • b 0+b 1 xi – предусмотренное моделью значения выхода.

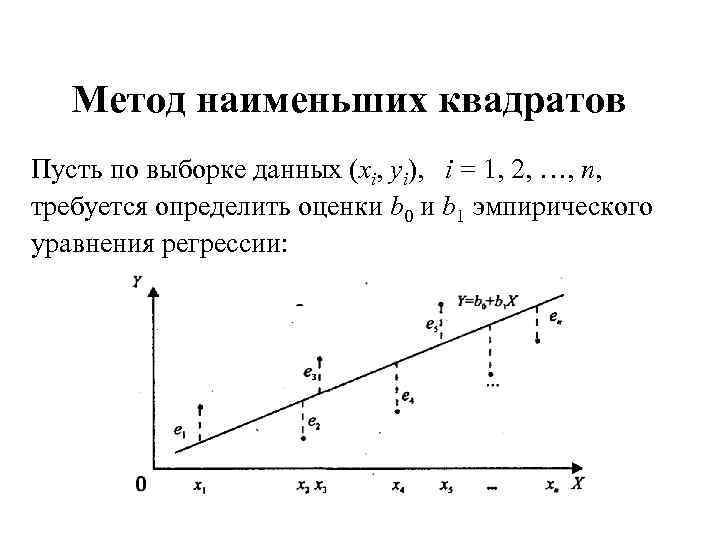Метод наименьших квадратов Пусть по выборке данных (xi, yi), i = 1, 2, , n, требуется определить оценки b 0 и b 1 эмпирического уравнения регрессии:

Процедура определения коэффициентов регрессии по методу наименьших квадратов предусматривает: • выбор типа кривой регрессии (аналитической формы); • определение частных производных зависимости по величинам коэффициентов регрессии; • приравнивание полученных выражений к нулю; • определение из полученной системы уравнений параметров регрессии; • проверка общего качества уравнения регрессии (коэф. Фишера); • проверка статистической значимости коэффициентов уравнения регрессии (статистика Стьюдента).

Метод наименьших квадратов Приравняем нулю частные производные и затем разделим на n оба уравнения:

Линейное уравнение регрессии • В случае одномерного процесса линейное уравнение регрессии и его коэффициенты рассчитываются в Excel по функциям : • НАКЛОН() – b 1 и ОТРЕЗОК() – b 0, • функцией массива ЛИНЕЙН(), • Анализ данных режимом РЕГРЕССИЯ.

Пример линейной регрессии-1 • В примере коэф. линии регрессии a, b рассчитаны по функциям НАКЛОН(), ОТРЕЗОК() и с использованием линии тренда.

Расчет регрессии с использованием функции ЛИНЕЙН() • 1 строка – коэффициенты регрессии; • 2 строка – стандартные ошибки для коэффициентов; • 3 строка –коэф. детерминации(R 2), стандартная ошибка для Y; • 4 –критерий Фишера расчетный; степени свободы; • 5 –суммы квадратов отклонений теор. от средних (SSфакториальная) и эмпирических от теоретических (SSостаточная).

Для определения адекватности уравнения (значимости) определяют дисперсии: • Общая дисперсия признака Y (MSY-дисперсия; SS-сумма квадратов отклонений; df-степени свободы) • Факторную дисперсию признака Y, отображает влияние только основных факторов MSф=SSф2/dfф; dfф=n-число наблюдений; • Остаточную дисперсию признака Y, отображает влияние остаточных факторов MSо=SSо 2/dfо. Dfо=n-(m+1) mчисло факторов • При корреляционной связи выполняется равенство: MS=SS 2/df

При корреляционной связи выхода и входов выполняется соотношение • Для анализа общего качества уравнения линейной регрессии используют множественный коэффициент детерминации R: • R определяет частицу вариации выхода, обусловленную изменением входов, которые входят в регрессионную модель, то есть показывает насколько хорошо модель описывает фактические данные, хорошее приближение отвечает 0, 71 и более.

Проверка адекватности уравнения • По результатам вычислений определяется расчетное значение Fр-критерия Фишера – 5772, 749; • Вычисляется табличное критическое значение Fкр = FРАСПОБР(0, 05; dfф; dfо), dfф=1(число факторов), dfо=n-(m+1)=9 -(1+1)=7. FРАСПОБР(0, 05; 1; 7)=5, 591 • Так как Fр>Fкр, Fр попадает в критический интервал (5, 591; ), то коэффициент детерминации значим, т. е. исследуемая зависимость существует.

Проверку параметров регрессии (коэффициентов) на значимость осуществляют с помощью критерия Стьюдента. • Проверяется попадание t-статистики расчетной в критическую область (tкр пр , ): • t-статистика расч=коэффициент/стандартная ошибка коэф; • t-статистика 1 =8, 183 /0, 108= 75, 98 • t-статистика 2 =4, 194 /0, 606= 6, 92 • Критическая область для коэффициентов: • tкр =СТЬЮДРАСПОБР(0, 05; 7)=2, 365 • (2, 365; ) –обе t-статистики попадают в эту область, т. е. • Коэффициенты значимы.

• • 2 способ оценки значимости коэффициентов: . Вычисляют доверительные интервалы для коэффициенов: (коэффициент-станд. ошибка* tкр; коэффициент+станд. ошибка* tкр) Для 1 коэффициента (8, 183) (=8, 183 -0, 108*2, 365; = 8, 183+0, 108*2, 365) или (7, 928; 8, 43); Для 2 коэффициента (4, 194) д. и. (2, 761; 5, 627) Если ai > t*Sai , где ai - коэффициент регрессии, t -значение статистики, Sai - стандартная ошибка коэффициента, то коэффициент значим. 8, 183> 0, 108*2, 365, 4, 194>1, 433, коэффициенты значимы.

Пример линейной регрессии-2

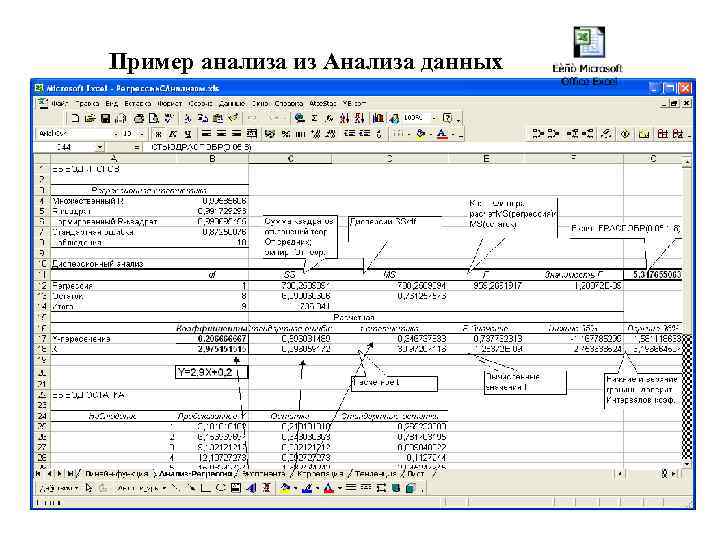Пример анализа из Анализа данных

Для определения величины степени взаимосвязи входа Х и выхода Y необходимо знать следующие дисперсии: • общую дисперсию выхода (Sy 2), которая отображает влияние как основных, так и остаточных факторов. ·дисперсию фактора выхода Y (Sф2), которая отображает влияние только основных факторов. ·остаточную дисперсию выхода Y (S 02), которая отображает влияние только не учтенных факторов: где – среднее значение выхода Y (мера разброса данных относительно среднего значения); Y– экспериментально наблюдаемый выход; y – теоретически предполагаемое значение выхода.

Экспоненциальная регрессия