 Регрессионный анализ
Регрессионный анализ
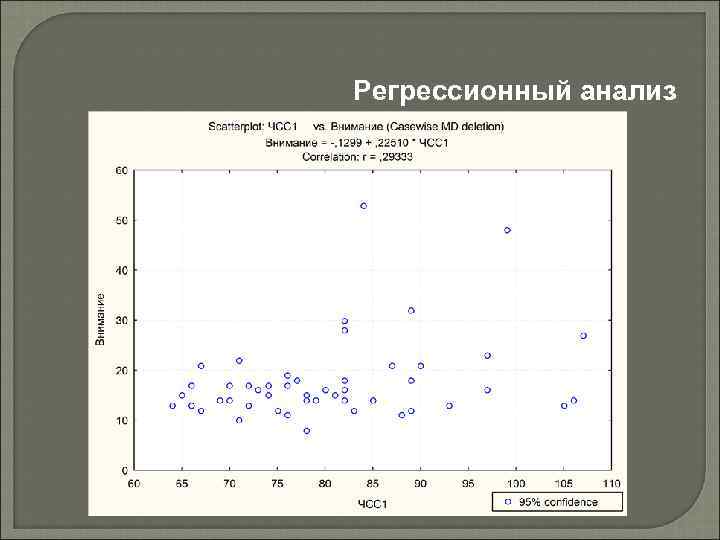 Регрессионный анализ
Регрессионный анализ
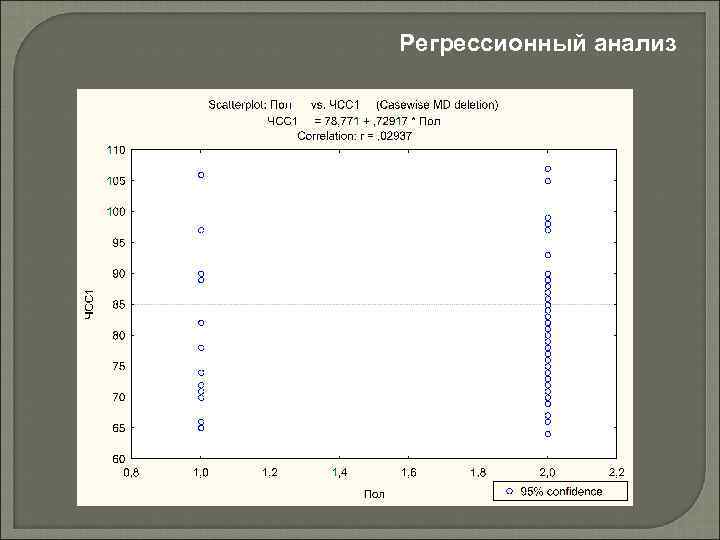 Регрессионный анализ
Регрессионный анализ
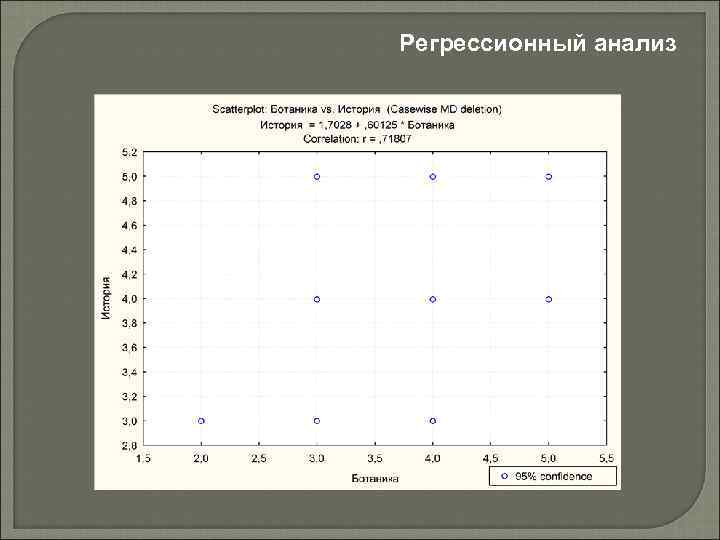 Регрессионный анализ
Регрессионный анализ
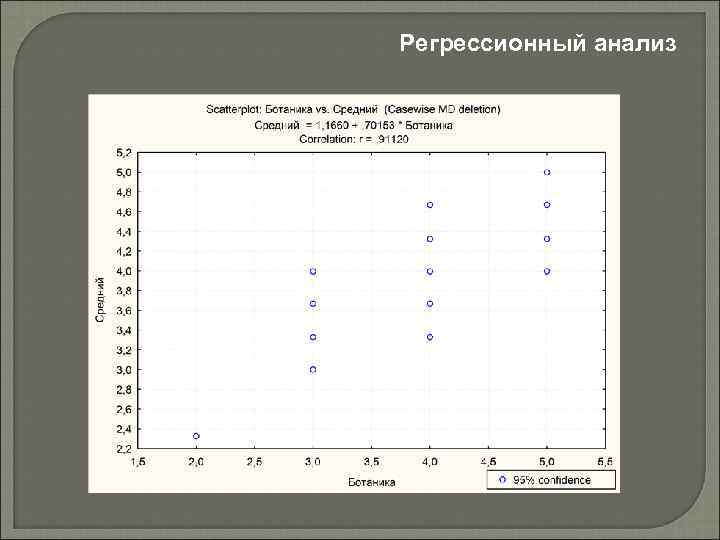 Регрессионный анализ
Регрессионный анализ
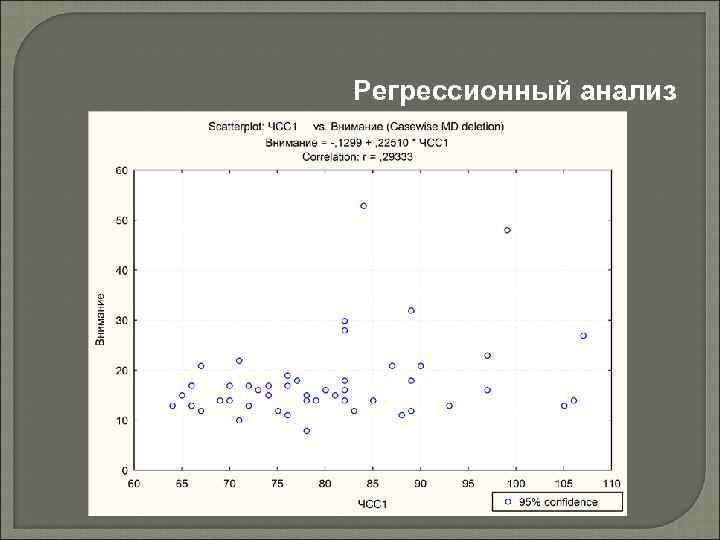 Регрессионный анализ
Регрессионный анализ
 Регрессионный анализ Число цветков при разном количестве неорганического брома в почве 2 4 6 8 10 12 14 Кол-во брома (мкг/см 3) Среднее число цветков 3, 6 2, 9 3, 2 1, 8 2, 3 1, 7 0, 8
Регрессионный анализ Число цветков при разном количестве неорганического брома в почве 2 4 6 8 10 12 14 Кол-во брома (мкг/см 3) Среднее число цветков 3, 6 2, 9 3, 2 1, 8 2, 3 1, 7 0, 8
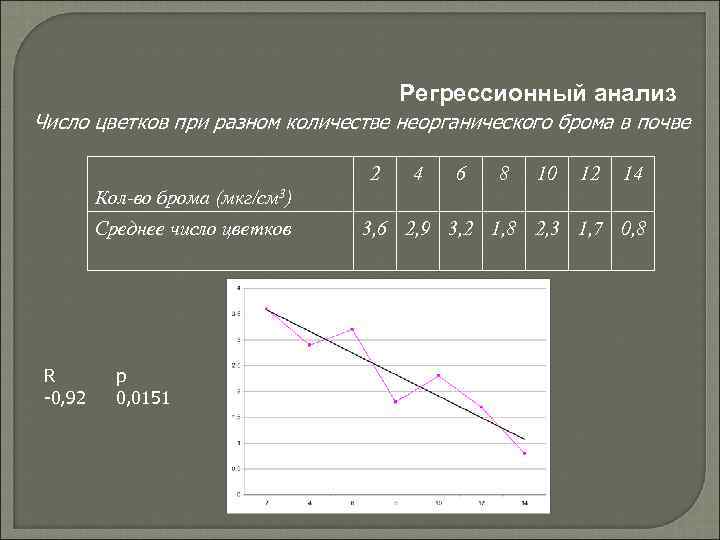 Регрессионный анализ Число цветков при разном количестве неорганического брома в почве 2 4 6 8 10 12 14 Кол-во брома (мкг/см 3) Среднее число цветков R -0, 92 p 0, 0151 3, 6 2, 9 3, 2 1, 8 2, 3 1, 7 0, 8
Регрессионный анализ Число цветков при разном количестве неорганического брома в почве 2 4 6 8 10 12 14 Кол-во брома (мкг/см 3) Среднее число цветков R -0, 92 p 0, 0151 3, 6 2, 9 3, 2 1, 8 2, 3 1, 7 0, 8
 Метод наименьших квадратов К. Гаусс и А. Лежандр y*=a+bx, где х – независимая переменная, т. е. , переменная, которую экспериментатор может менять по своему усмотрению; y* - зависимая переменная или отклик; a и b – коэффициенты (параметры).
Метод наименьших квадратов К. Гаусс и А. Лежандр y*=a+bx, где х – независимая переменная, т. е. , переменная, которую экспериментатор может менять по своему усмотрению; y* - зависимая переменная или отклик; a и b – коэффициенты (параметры).
 Метод наименьших квадратов каждому значению независимой переменной в общем случае соответствует ошибка: i=yi-yi*
Метод наименьших квадратов каждому значению независимой переменной в общем случае соответствует ошибка: i=yi-yi*
 Метод наименьших квадратов 2 4 6 8 10 12 14 3, 6 2, 9 3, 2 1, 8 2, 3 1, 7 0, 8 Кол-во брома (мкг/см 3) Среднее число цветков 16, 3=7 a+56 b 107=56 a+560 b Откуда a=4, b=-0, 209
Метод наименьших квадратов 2 4 6 8 10 12 14 3, 6 2, 9 3, 2 1, 8 2, 3 1, 7 0, 8 Кол-во брома (мкг/см 3) Среднее число цветков 16, 3=7 a+56 b 107=56 a+560 b Откуда a=4, b=-0, 209
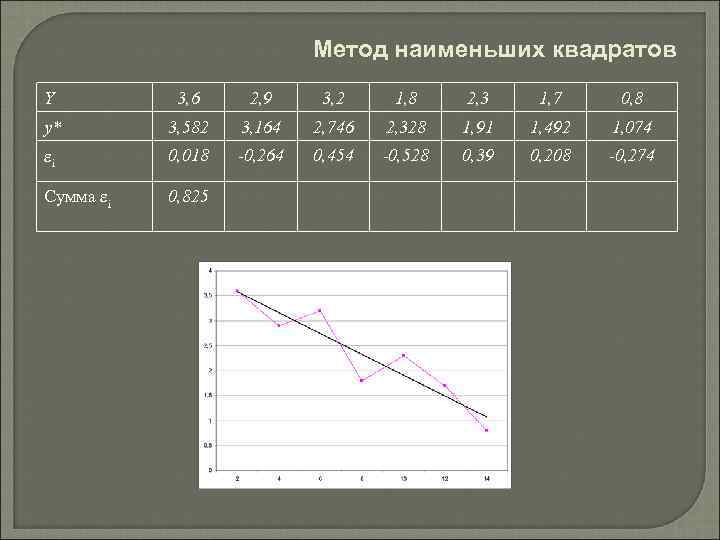 Метод наименьших квадратов Y 3, 6 2, 9 3, 2 1, 8 2, 3 1, 7 0, 8 y* 3, 582 3, 164 2, 746 2, 328 1, 91 1, 492 1, 074 i 0, 018 -0, 264 0, 454 -0, 528 0, 39 0, 208 -0, 274 Сумма i 0, 825
Метод наименьших квадратов Y 3, 6 2, 9 3, 2 1, 8 2, 3 1, 7 0, 8 y* 3, 582 3, 164 2, 746 2, 328 1, 91 1, 492 1, 074 i 0, 018 -0, 264 0, 454 -0, 528 0, 39 0, 208 -0, 274 Сумма i 0, 825
 Метод наименьших квадратов
Метод наименьших квадратов
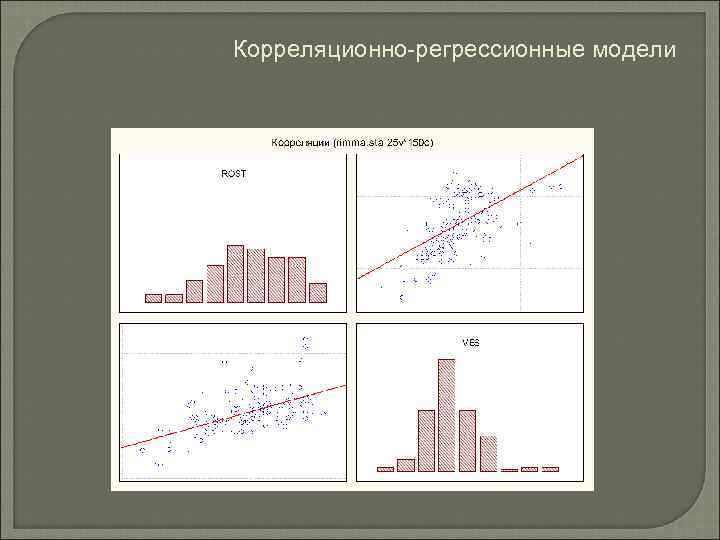 Корреляционно-регрессионные модели
Корреляционно-регрессионные модели
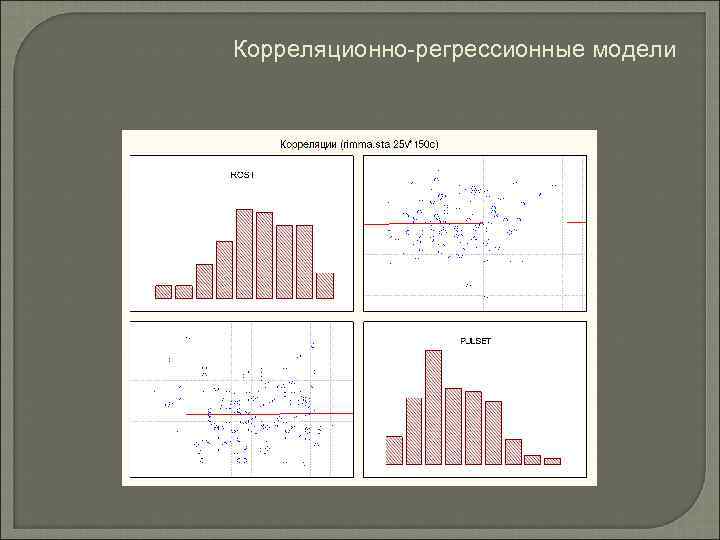 Корреляционно-регрессионные модели
Корреляционно-регрессионные модели
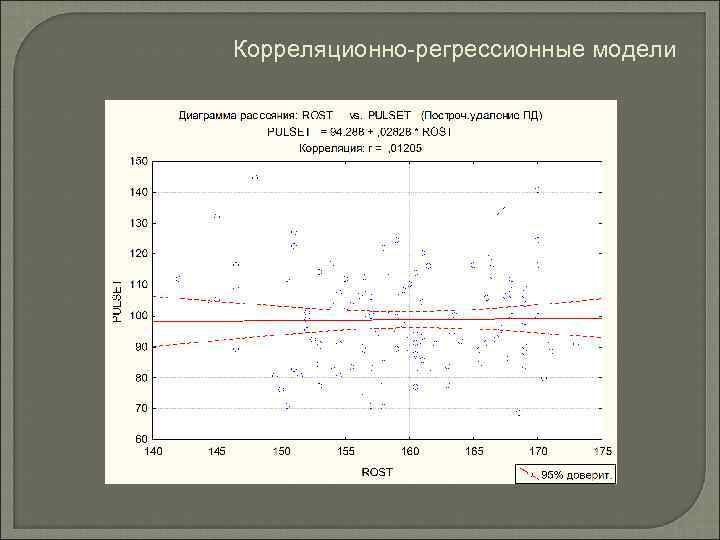 Корреляционно-регрессионные модели
Корреляционно-регрессионные модели
 Корреляционно-регрессионные модели y=a+bx+cx 2 y=abx y=axb y=x/(a+bx)
Корреляционно-регрессионные модели y=a+bx+cx 2 y=abx y=axb y=x/(a+bx)
 Частные коэффициенты корреляции Артериальное давление 1 -0, 41 Вес 3 -0, 59 0, 91 Возраст 2
Частные коэффициенты корреляции Артериальное давление 1 -0, 41 Вес 3 -0, 59 0, 91 Возраст 2
 Частные коэффициенты корреляции Артериальное давление 1 -0, 41 Вес 3 -0, 59 0, 91 Возраст 2
Частные коэффициенты корреляции Артериальное давление 1 -0, 41 Вес 3 -0, 59 0, 91 Возраст 2