РЕГРЕССИОННЫЙ АНАЛИЗ 1 Различают два типа связей между


























































regr.ppt
- Количество слайдов: 70
 РЕГРЕССИОННЫЙ АНАЛИЗ 1
РЕГРЕССИОННЫЙ АНАЛИЗ 1
 Различают два типа связей между различными явлениями и их признаками: функциональную и статистическую Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения других (другой), и эти другие величины принимают некоторые значения с определенными вероятностями. Функциональной называют зависимость, в которой значению одной переменной обязательно соответствует одно или несколько точно заданных значений другой переменной. В общем виде y = f(x), где y – зависимая переменная, или функция от независимой переменной x 2
Различают два типа связей между различными явлениями и их признаками: функциональную и статистическую Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения других (другой), и эти другие величины принимают некоторые значения с определенными вероятностями. Функциональной называют зависимость, в которой значению одной переменной обязательно соответствует одно или несколько точно заданных значений другой переменной. В общем виде y = f(x), где y – зависимая переменная, или функция от независимой переменной x 2
 Корреляционная зависимость, характеризующая взаимосвязь значений одних случайных величин со средним значением других, хотя в каждом отдельном случае любая взаимосвязанная величина может принимать различные значения. Если же у взаимосвязанных величин вариацию имеет только одна переменная, а другая является детерминированной (т.е. строго определенной), то такую связь называют не корреляционной, а регрессионной. 3
Корреляционная зависимость, характеризующая взаимосвязь значений одних случайных величин со средним значением других, хотя в каждом отдельном случае любая взаимосвязанная величина может принимать различные значения. Если же у взаимосвязанных величин вариацию имеет только одна переменная, а другая является детерминированной (т.е. строго определенной), то такую связь называют не корреляционной, а регрессионной. 3
 Задачи корреляционного анализа: 1) измерение параметров уравнения, выражающего связь средних значений зависимой переменной со значениями независимой переменной; 2) измерение тесноты связи двух (или большего числа) признаков между собой. Вторая задача специфична для статистических связей (корреляционный анализ), а первая разработана для функциональных связей и является общей (корреляционный и регрессионный анализ). Для измерения тесноты связи применяется несколько показателей, например коэффициент корреляции. Корреляционная связь между признаками может быть линейной и нелинейной, положительной и отрицательной. 4
Задачи корреляционного анализа: 1) измерение параметров уравнения, выражающего связь средних значений зависимой переменной со значениями независимой переменной; 2) измерение тесноты связи двух (или большего числа) признаков между собой. Вторая задача специфична для статистических связей (корреляционный анализ), а первая разработана для функциональных связей и является общей (корреляционный и регрессионный анализ). Для измерения тесноты связи применяется несколько показателей, например коэффициент корреляции. Корреляционная связь между признаками может быть линейной и нелинейной, положительной и отрицательной. 4
 Графическая интерпретация взаимосвязи между показателями
Графическая интерпретация взаимосвязи между показателями
 Регрессионный (линейный) анализ — статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X1,X2,...,Xp. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения. 6
Регрессионный (линейный) анализ — статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X1,X2,...,Xp. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения. 6
 Цели регрессионного анализа Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными) Предсказание значения зависимой переменной с помощью независимой(-ых) Определение вклада отдельных независимых переменных в вариацию зависимой Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа. 7
Цели регрессионного анализа Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными) Предсказание значения зависимой переменной с помощью независимой(-ых) Определение вклада отдельных независимых переменных в вариацию зависимой Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа. 7
 Термин регрессия был введен Фрэнсисом Гальтоном в конце 19-го века. После работ Карла Пирсона этот термин стал использоваться в статистике. Регрессия вводит понятие случайной переменной. Предполагается, что зависимая переменная (переменная отклика) является функцией свободной (объясняющей) переменной с добавлением случайной переменной, которая измеряется по некоторому закону распределения. РЕГРЕССИОННЫЙ АНАЛИЗ 8
Термин регрессия был введен Фрэнсисом Гальтоном в конце 19-го века. После работ Карла Пирсона этот термин стал использоваться в статистике. Регрессия вводит понятие случайной переменной. Предполагается, что зависимая переменная (переменная отклика) является функцией свободной (объясняющей) переменной с добавлением случайной переменной, которая измеряется по некоторому закону распределения. РЕГРЕССИОННЫЙ АНАЛИЗ 8
 МАТЕМАТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ РЕГРЕССИИ Строго регрессионную зависимость можно определить следующим образом. Пусть Y, X1,X2,...,Xp случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений X1 = x1,X2 = x2,...,Xp = xp определено условное математическое ожидание y(x1,x2,...,xp) = E(Y | X1 = x1,X2 = x2,...,Xp = xp) (уравнение линейной регрессии в общем виде), то функция y(x1,x2,...,xp) называется регрессией величины Y по величинам X1,X2,...,Xp, а её график — линией регрессии Y по X1,X2,...,Xp, или уравнением регрессии. Зависимость Y от X1,X2,...,Xp проявляется в изменении средних значений Y при изменении X1,X2,...,Xp. Хотя при каждом фиксированном наборе значений X1 = x1,X2 = x2,...,Xp = xp величина Y остаётся случайной величиной с определённым рассеянием. 9
МАТЕМАТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ РЕГРЕССИИ Строго регрессионную зависимость можно определить следующим образом. Пусть Y, X1,X2,...,Xp случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений X1 = x1,X2 = x2,...,Xp = xp определено условное математическое ожидание y(x1,x2,...,xp) = E(Y | X1 = x1,X2 = x2,...,Xp = xp) (уравнение линейной регрессии в общем виде), то функция y(x1,x2,...,xp) называется регрессией величины Y по величинам X1,X2,...,Xp, а её график — линией регрессии Y по X1,X2,...,Xp, или уравнением регрессии. Зависимость Y от X1,X2,...,Xp проявляется в изменении средних значений Y при изменении X1,X2,...,Xp. Хотя при каждом фиксированном наборе значений X1 = x1,X2 = x2,...,Xp = xp величина Y остаётся случайной величиной с определённым рассеянием. 9
 РЕГРЕССИОННЫЙ АНАЛИЗ Задача нахождения регрессионной зависимости ставится, к примеру, следующим образом: Дана конечная выборка – множество пар значений свободной переменной и зависимой переменной . Требуется найти функцию , для которой справедливо равенство наиболее узкую (обычно в среднеквадратичном) до математического ожидания зависимой переменной для каждого значения свободной переменной. Функция отыскивается в заданном семействе функций. Выборка может быть не функцией, а отношением. 10
РЕГРЕССИОННЫЙ АНАЛИЗ Задача нахождения регрессионной зависимости ставится, к примеру, следующим образом: Дана конечная выборка – множество пар значений свободной переменной и зависимой переменной . Требуется найти функцию , для которой справедливо равенство наиболее узкую (обычно в среднеквадратичном) до математического ожидания зависимой переменной для каждого значения свободной переменной. Функция отыскивается в заданном семействе функций. Выборка может быть не функцией, а отношением. 10
 Данные для построения регрессии могут быть такими: {(0, 0), (0,1), (0, 2), (1, 1), (1, 2), (1, 3)}. В такой выборке одному значению переменной х соответствует несколько значений переменной у. РЕГРЕССИОННЫЙ АНАЛИЗ ПРИМЕР Рис.1. Регрессия, функция f определена математическим ожиданием зависимой переменной 11
Данные для построения регрессии могут быть такими: {(0, 0), (0,1), (0, 2), (1, 1), (1, 2), (1, 3)}. В такой выборке одному значению переменной х соответствует несколько значений переменной у. РЕГРЕССИОННЫЙ АНАЛИЗ ПРИМЕР Рис.1. Регрессия, функция f определена математическим ожиданием зависимой переменной 11
 В статистической литературе различают регрессию с участием одной свободной переменной и с несколькими свободными переменными — одномерную и многомерную регрессию. РЕГРЕССИОННЫЙ АНАЛИЗ Обычно используют несколько свободных переменных, то есть, свободная переменная — вектор . В частных случаях, когда свободная переменная является скаляром, она будет обозначаться х. Различают линейную и нелинейную регрессию. В первом случае переменная зависит от линейной комбинации свободных переменных, Здесь — некоторая функция. Если регрессионную модель не является линейной комбинацией функций от свободной переменной, то говорят о нелинейной регрессии. 12
В статистической литературе различают регрессию с участием одной свободной переменной и с несколькими свободными переменными — одномерную и многомерную регрессию. РЕГРЕССИОННЫЙ АНАЛИЗ Обычно используют несколько свободных переменных, то есть, свободная переменная — вектор . В частных случаях, когда свободная переменная является скаляром, она будет обозначаться х. Различают линейную и нелинейную регрессию. В первом случае переменная зависит от линейной комбинации свободных переменных, Здесь — некоторая функция. Если регрессионную модель не является линейной комбинацией функций от свободной переменной, то говорят о нелинейной регрессии. 12
 Нелинейными моделями являются например, экспоненциальные, тригонометрические и другие, если полагать зависимость между свободной и зависимой переменной нелинейной. РЕГРЕССИОННЫЙ АНАЛИЗ Различают параметрическую и непараметрическую регрессию. Строгую границу между этими двумя типами регрессий провести сложно. Сейчас нет общепринятого критерия отличия одного типа моделей от другого. Например, считается, что линейные модели являются параметрическими, а модели, включающие усреднение зависимой переменной по пространству свободной переменной — непараметрическими. В целом, непараметрическая регрессия отличается от параметрической тем, что зависимая переменная зависит не от одного значения свободной переменной, а от некоторой заданной окрестности этого значения. 13
Нелинейными моделями являются например, экспоненциальные, тригонометрические и другие, если полагать зависимость между свободной и зависимой переменной нелинейной. РЕГРЕССИОННЫЙ АНАЛИЗ Различают параметрическую и непараметрическую регрессию. Строгую границу между этими двумя типами регрессий провести сложно. Сейчас нет общепринятого критерия отличия одного типа моделей от другого. Например, считается, что линейные модели являются параметрическими, а модели, включающие усреднение зависимой переменной по пространству свободной переменной — непараметрическими. В целом, непараметрическая регрессия отличается от параметрической тем, что зависимая переменная зависит не от одного значения свободной переменной, а от некоторой заданной окрестности этого значения. 13
 РЕГРЕССИОННЫЙ АНАЛИЗ Дана функция и дискретного или непрерывного аргумента. Требуется найти функцию из некоторого параметрическую семейства, например, среди алгебраических полиномов заданной степени. Параметры функции должны доставлять минимум некоторому функционалу, например, Приближение функций. Термин аппроксимация — синоним термина «приближение функций». Чаще используется тогда, когда речь идет о заданной функции, как о функции дискретного аргумента. Здесь также требуется отыскать такую функцию , которая проходит наиболее близко ко всем точкам заданной функции. При этом вводится понятие невязки — расстояния между точками непрерывной функции и соответствующими точками функции и дискретного аргумента. 14
РЕГРЕССИОННЫЙ АНАЛИЗ Дана функция и дискретного или непрерывного аргумента. Требуется найти функцию из некоторого параметрическую семейства, например, среди алгебраических полиномов заданной степени. Параметры функции должны доставлять минимум некоторому функционалу, например, Приближение функций. Термин аппроксимация — синоним термина «приближение функций». Чаще используется тогда, когда речь идет о заданной функции, как о функции дискретного аргумента. Здесь также требуется отыскать такую функцию , которая проходит наиболее близко ко всем точкам заданной функции. При этом вводится понятие невязки — расстояния между точками непрерывной функции и соответствующими точками функции и дискретного аргумента. 14
 РЕГРЕССИОННЫЙ АНАЛИЗ Интерполяция функций — частный случай задачи приближения, когда требуется, чтобы в определенных точках, называемых узлами интерполяции совпадали значения функции и приближающей ее функции . В более общем случае накладываются ограничения на значения некоторых производных производных функции. То есть дана функция дискретного аргумента. Требуется отыскать такую функцию , которая проходит через все точки . Рис.2. Аппроксимация функций непрерывная функция приближает непрерывную или дискретную функцию 15
РЕГРЕССИОННЫЙ АНАЛИЗ Интерполяция функций — частный случай задачи приближения, когда требуется, чтобы в определенных точках, называемых узлами интерполяции совпадали значения функции и приближающей ее функции . В более общем случае накладываются ограничения на значения некоторых производных производных функции. То есть дана функция дискретного аргумента. Требуется отыскать такую функцию , которая проходит через все точки . Рис.2. Аппроксимация функций непрерывная функция приближает непрерывную или дискретную функцию 15
 РЕГРЕССИОННЫЙ АНАЛИЗ Рис 3. Интерполяция, функция задана значениями узловых точек Регрессия и классификация тесно связаны друг с другом. Термин алгоритм в классификации мог бы стать синонимом термина модель в регрессии, если бы не алгоритм не оперировал с дискретным множеством ответов-классов, а модель — с непрерывно-определенной свободной переменной. При этом метрика обычно не используется. Однако часто вводится понятие "гладкости" искомой функции. 16
РЕГРЕССИОННЫЙ АНАЛИЗ Рис 3. Интерполяция, функция задана значениями узловых точек Регрессия и классификация тесно связаны друг с другом. Термин алгоритм в классификации мог бы стать синонимом термина модель в регрессии, если бы не алгоритм не оперировал с дискретным множеством ответов-классов, а модель — с непрерывно-определенной свободной переменной. При этом метрика обычно не используется. Однако часто вводится понятие "гладкости" искомой функции. 16
 МЕТОД НАИМЕНЬШИХ КВАДРАТОВ На практике линия регрессии ищется в виде некоторой функции, чаще всего линейной Y = b0 + b1X1 + b2X2 + ... + bNXN (т.н. линейная регрессия), наилучшим образом приближающей искомую кривую. Коэффициенты регрессии находятся с использованием метода наименьших квадратов. В данном методе минимизируется сумма квадратов отклонений реально наблюдаемых значений от их оценок Подход основан на том факте, что фигурирующая в приведённом выражении сумма принимает минимальное значение именно для того случая, когда Y = y(x1,x2,...xN). 17
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ На практике линия регрессии ищется в виде некоторой функции, чаще всего линейной Y = b0 + b1X1 + b2X2 + ... + bNXN (т.н. линейная регрессия), наилучшим образом приближающей искомую кривую. Коэффициенты регрессии находятся с использованием метода наименьших квадратов. В данном методе минимизируется сумма квадратов отклонений реально наблюдаемых значений от их оценок Подход основан на том факте, что фигурирующая в приведённом выражении сумма принимает минимальное значение именно для того случая, когда Y = y(x1,x2,...xN). 17
 МЕТОД НАИМЕНЬШИХ КВАДРАТОВ Для решения задачи регрессионного анализа методом наименьших квадратов вводится понятие функции невязки: Из условия минимума функции невязки находятся коэффициенты регрессионной зависимости 18
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ Для решения задачи регрессионного анализа методом наименьших квадратов вводится понятие функции невязки: Из условия минимума функции невязки находятся коэффициенты регрессионной зависимости 18
 Интерпретация параметров регрессии Параметры bi являются частными коэффициентами корреляции; (bi)2 интерпретируется как доля дисперсии Y, объяснённая Xi, при закреплении влияния остальных предикторов, то есть измеряет индивидуальный вклад Xi в объяснение Y. В случае коррелирующих предикторов возникает проблема неопределённости в оценках, которые становятся зависимыми от порядка включения предикторов в модель. В таких случаях необходимо применение методов анализа корреляционного и пошагового регрессионного анализа. Говоря о нелинейных моделях регрессионного анализа, важно обращать внимание на то, идет ли речь о нелинейности по независимым переменным (с формальной точки зрения легко сводящейся к линейной регрессии), или о нелинейности по оцениваемым параметрам (вызывающей серьёзные вычислительные трудности). При нелинейности первого вида с содержательной точки зрения важно выделять появление в модели членов вида X1X2, X1X2X3, свидетельствующее о наличии взаимодействий между признаками X1, X2 и т. д. 19
Интерпретация параметров регрессии Параметры bi являются частными коэффициентами корреляции; (bi)2 интерпретируется как доля дисперсии Y, объяснённая Xi, при закреплении влияния остальных предикторов, то есть измеряет индивидуальный вклад Xi в объяснение Y. В случае коррелирующих предикторов возникает проблема неопределённости в оценках, которые становятся зависимыми от порядка включения предикторов в модель. В таких случаях необходимо применение методов анализа корреляционного и пошагового регрессионного анализа. Говоря о нелинейных моделях регрессионного анализа, важно обращать внимание на то, идет ли речь о нелинейности по независимым переменным (с формальной точки зрения легко сводящейся к линейной регрессии), или о нелинейности по оцениваемым параметрам (вызывающей серьёзные вычислительные трудности). При нелинейности первого вида с содержательной точки зрения важно выделять появление в модели членов вида X1X2, X1X2X3, свидетельствующее о наличии взаимодействий между признаками X1, X2 и т. д. 19





 Многомерный регрессионный анализ был разработан для прогнозирования экономической активности в различных отраслях экономики (денежные потоки, уровни доходов, банковские ставки, уровень рождаемости, безработицы и т.д.) полезен для прогнозов будущих тенденций и для оценки и корректировки текущей стратегии (оценки настоящего)
Многомерный регрессионный анализ был разработан для прогнозирования экономической активности в различных отраслях экономики (денежные потоки, уровни доходов, банковские ставки, уровень рождаемости, безработицы и т.д.) полезен для прогнозов будущих тенденций и для оценки и корректировки текущей стратегии (оценки настоящего)
 Многомерная регрессия Для прогноза зависимой переменной используется более одной независимой переменной Признаки хорошей независимой переменной: связанна с зависимой переменной не имеет тесной связи с любой другой независимой переменной Мультиколлинеарность
Многомерная регрессия Для прогноза зависимой переменной используется более одной независимой переменной Признаки хорошей независимой переменной: связанна с зависимой переменной не имеет тесной связи с любой другой независимой переменной Мультиколлинеарность
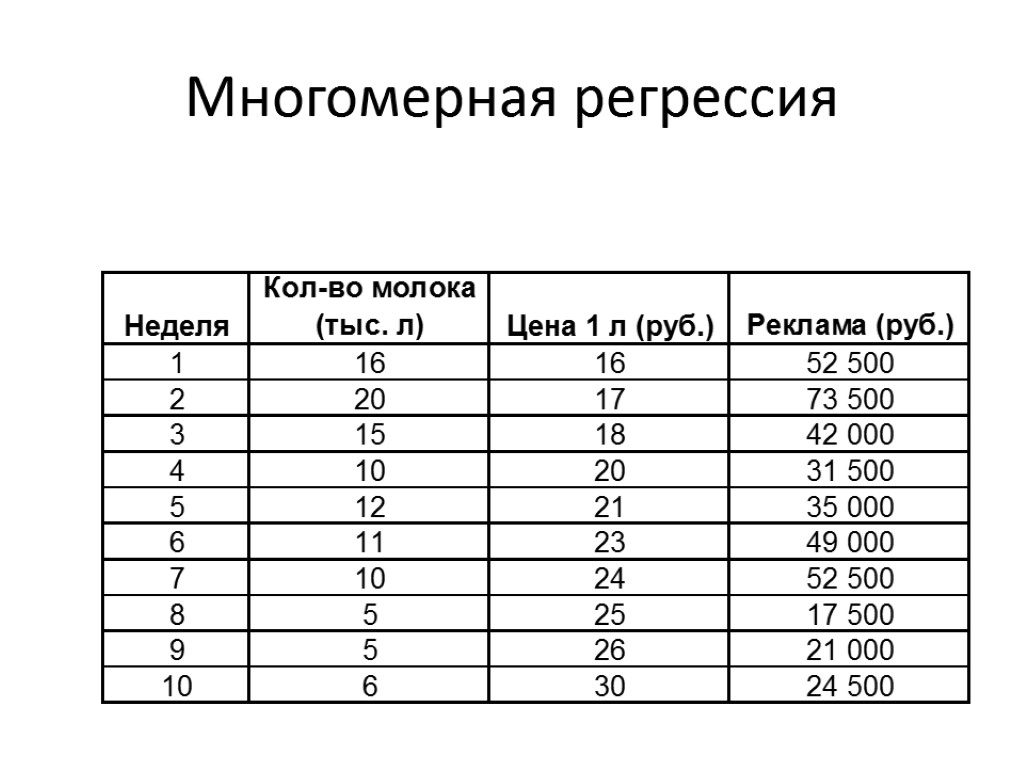
 Многомерная регрессия Зависимая переменная – объем продаж молока Независимые переменные: цена за 1 л, расходы на рекламу
Многомерная регрессия Зависимая переменная – объем продаж молока Независимые переменные: цена за 1 л, расходы на рекламу
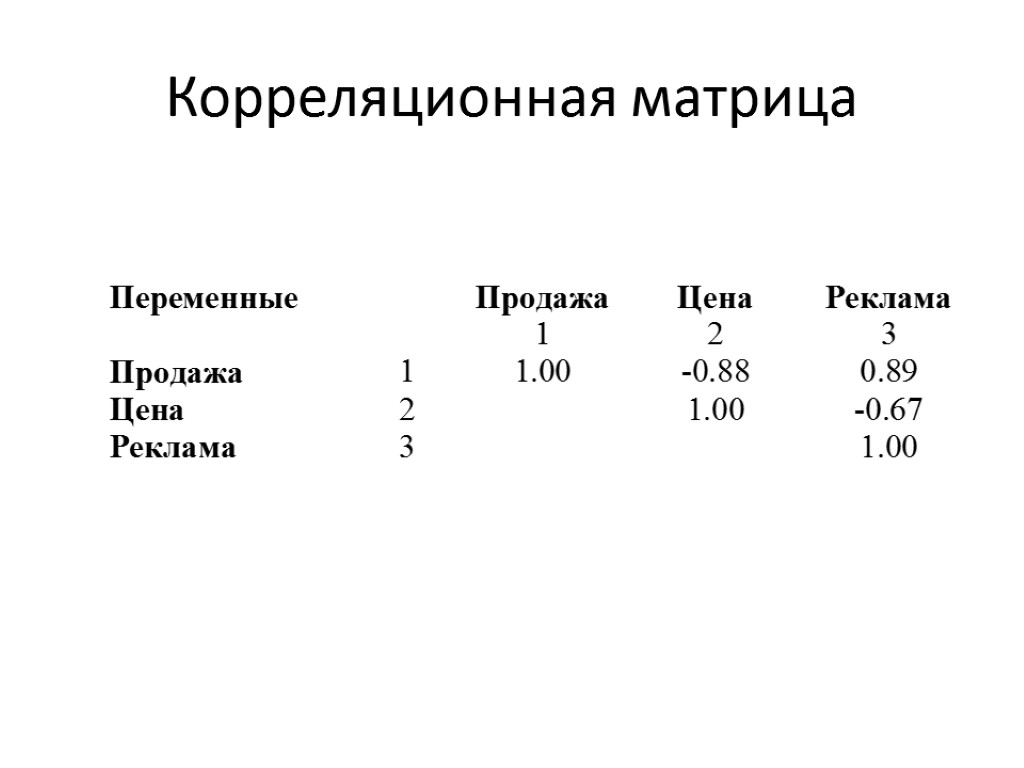
 Многомерная регрессия Корреляционная матрица составляется из коэффициентов корреляции, вычисленных для каждой возможной пары переменных r12 = r21 и т. д. r11 = r22 = r33 = 1
Многомерная регрессия Корреляционная матрица составляется из коэффициентов корреляции, вычисленных для каждой возможной пары переменных r12 = r21 и т. д. r11 = r22 = r33 = 1
 Многомерная регрессия
Многомерная регрессия
 Корреляционная матрица
Корреляционная матрица
 Многомерная регрессионная модель Математическое ожидание зависимой величины является линейной функцией всех объясняющих ее переменных Многомерная регрессионная функция генеральной совокупности
Многомерная регрессионная модель Математическое ожидание зависимой величины является линейной функцией всех объясняющих ее переменных Многомерная регрессионная функция генеральной совокупности
 Многомерная регрессионная модель Статистическая модель многомерной регрессии Метод наименьших квадратов
Многомерная регрессионная модель Статистическая модель многомерной регрессии Метод наименьших квадратов
 Многомерная регрессионная модель Пример с молоком
Многомерная регрессионная модель Пример с молоком
 Интерпретация коэффициентов регрессии b0 – свободный член (значение при Х1 и Х2, равных нулю) b1 и b2 – частные или чистые коэффициенты регрессии (среднее изменение при единичном изменении соответствующей независимой переменной и постоянных значениях других независимых переменных)
Интерпретация коэффициентов регрессии b0 – свободный член (значение при Х1 и Х2, равных нулю) b1 и b2 – частные или чистые коэффициенты регрессии (среднее изменение при единичном изменении соответствующей независимой переменной и постоянных значениях других независимых переменных)
 Статистический анализ модели многомерной регрессии вычисления проводятся на компьютере
Статистический анализ модели многомерной регрессии вычисления проводятся на компьютере
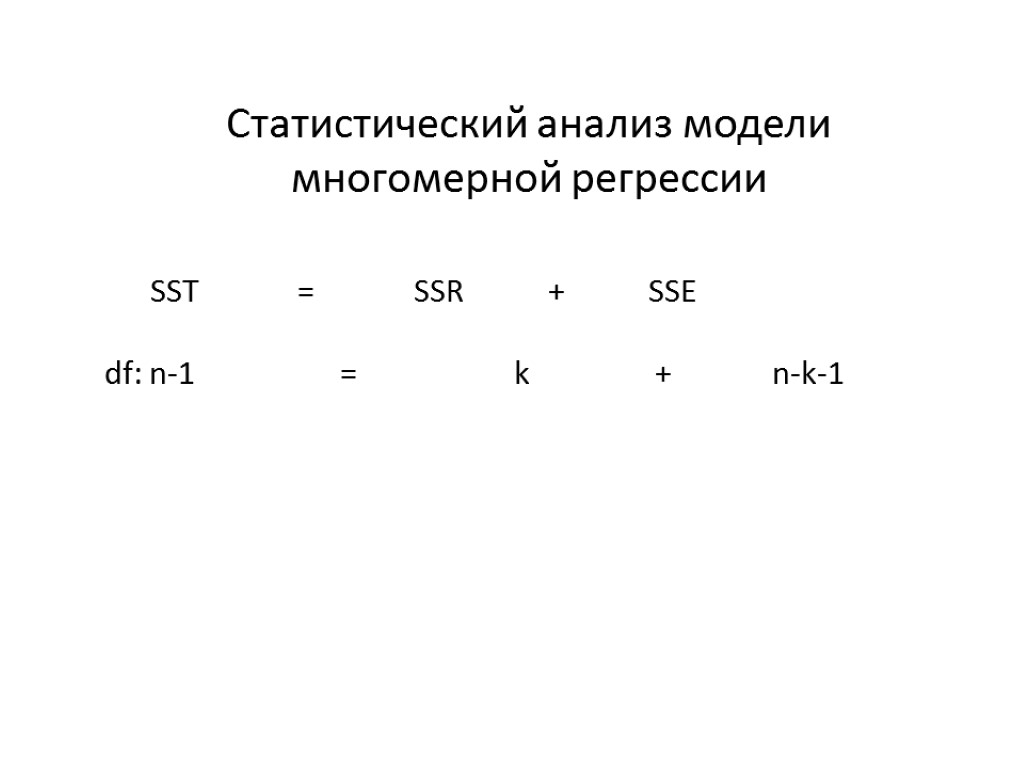
 Статистический анализ модели многомерной регрессии SST = SSR + SSE df: n-1 = k + n-k-1
Статистический анализ модели многомерной регрессии SST = SSR + SSE df: n-1 = k + n-k-1
 Стандартная ошибка оценки Стандартная ошибка оценки измеряет отклонение имеющихся данных (Y) от их оценок ( )
Стандартная ошибка оценки Стандартная ошибка оценки измеряет отклонение имеющихся данных (Y) от их оценок ( )
 Стандартная ошибка оценки Пример с молоком: 2 независимые переменные: цена за 1 л и расходы на рекламу стандартная ошибка оценки = 1.42 1 независимая переменная: цена 1 л стандартная ошибка оценки = 2.5 Вывод: использование многомерной регрессии позволяет сделать более точный прогноз
Стандартная ошибка оценки Пример с молоком: 2 независимые переменные: цена за 1 л и расходы на рекламу стандартная ошибка оценки = 1.42 1 независимая переменная: цена 1 л стандартная ошибка оценки = 2.5 Вывод: использование многомерной регрессии позволяет сделать более точный прогноз
 Значимость регрессии
Значимость регрессии
 Значимость регрессии Гипотезы: df=k, n-k-1
Значимость регрессии Гипотезы: df=k, n-k-1
 Значимость регрессии Коэффициент детерминации Многомерный коэффициент корреляции (характеризует корреляцию между зависимой переменной и прогнозом) Для многомерной регрессии
Значимость регрессии Коэффициент детерминации Многомерный коэффициент корреляции (характеризует корреляцию между зависимой переменной и прогнозом) Для многомерной регрессии
 Значимость регрессии Пример с молоком Две независимые переменные SST=SSR+SSE 222=207.86+14.14 R2=0.94 Одна независимая переменная SST=SSR+SSE 222=172.023+49.977 R2=0.77
Значимость регрессии Пример с молоком Две независимые переменные SST=SSR+SSE 222=207.86+14.14 R2=0.94 Одна независимая переменная SST=SSR+SSE 222=172.023+49.977 R2=0.77
 Отдельные независимые переменные Проверочная статистика t df = n-k-1
Отдельные независимые переменные Проверочная статистика t df = n-k-1
 Прогнозирование будущих значений зависимой переменной Границы интервала прогноза величины Y:
Прогнозирование будущих значений зависимой переменной Границы интервала прогноза величины Y:
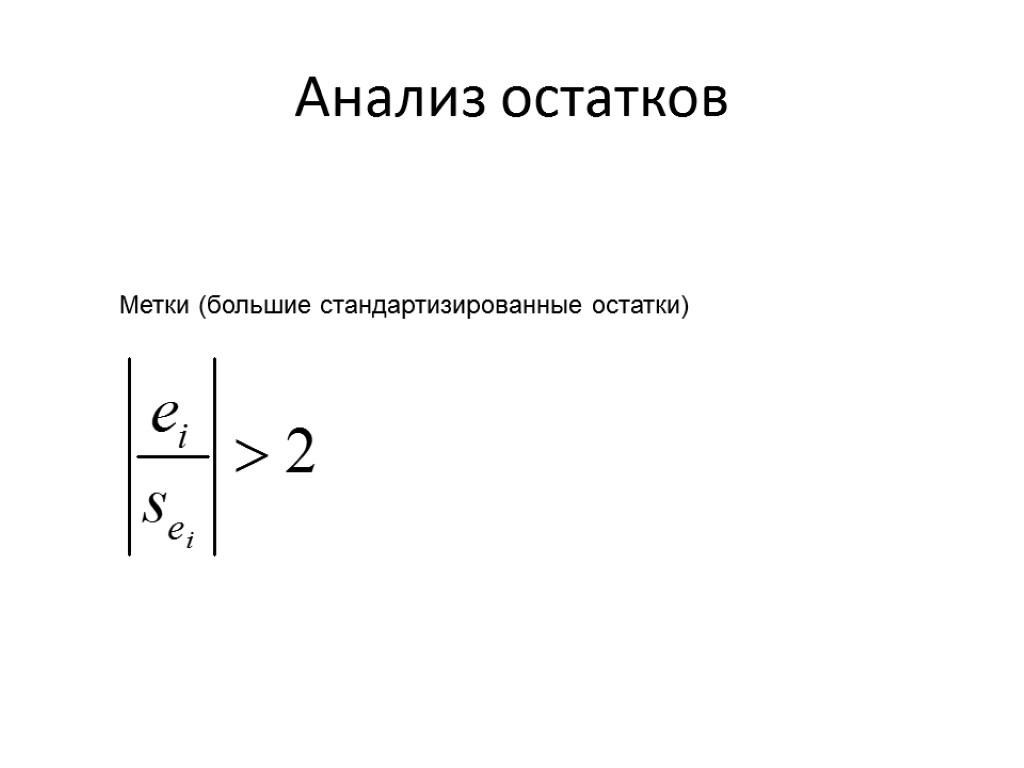
 Анализ остатков Рычаг – мера влияния i-й точки данных на положение функции регрессии Стандартизированный остаток
Анализ остатков Рычаг – мера влияния i-й точки данных на положение функции регрессии Стандартизированный остаток
 Анализ остатков Метки (большие стандартизированные остатки)
Анализ остатков Метки (большие стандартизированные остатки)
 Предостережения при прогнозировании прогнозирование вне допустимого множества небольшой объем выборки большое количество независимых переменных в идеале – 10 наблюдений на одну независимую переменную вычисление функции регрессии для одной части данных и проверка ее на оставшихся данных при уровне значимости 0,05 отношение F было хотя бы в 4 раза больше соответствующего критического значения
Предостережения при прогнозировании прогнозирование вне допустимого множества небольшой объем выборки большое количество независимых переменных в идеале – 10 наблюдений на одну независимую переменную вычисление функции регрессии для одной части данных и проверка ее на оставшихся данных при уровне значимости 0,05 отношение F было хотя бы в 4 раза больше соответствующего критического значения
 Фиктивные переменные
Фиктивные переменные
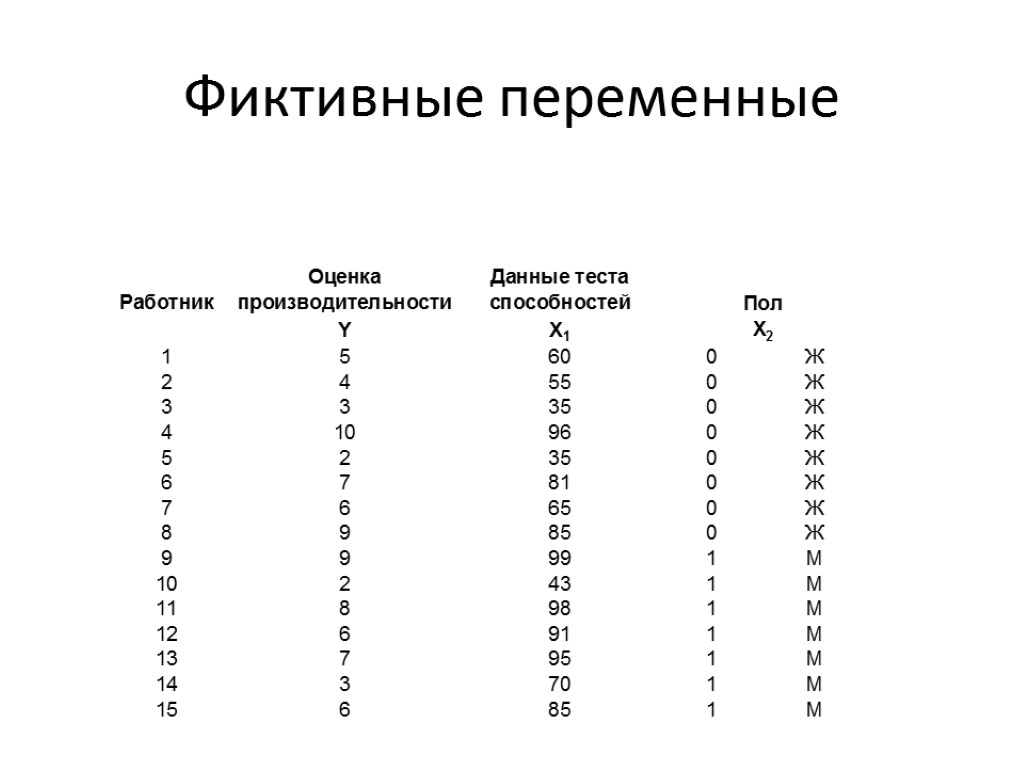
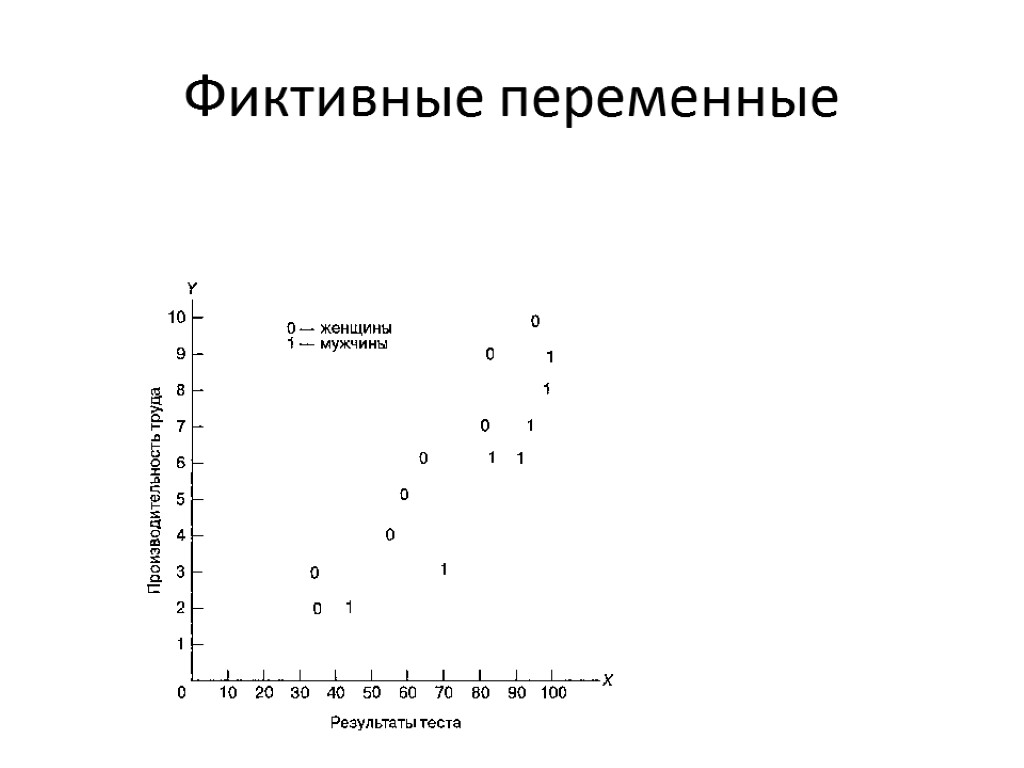
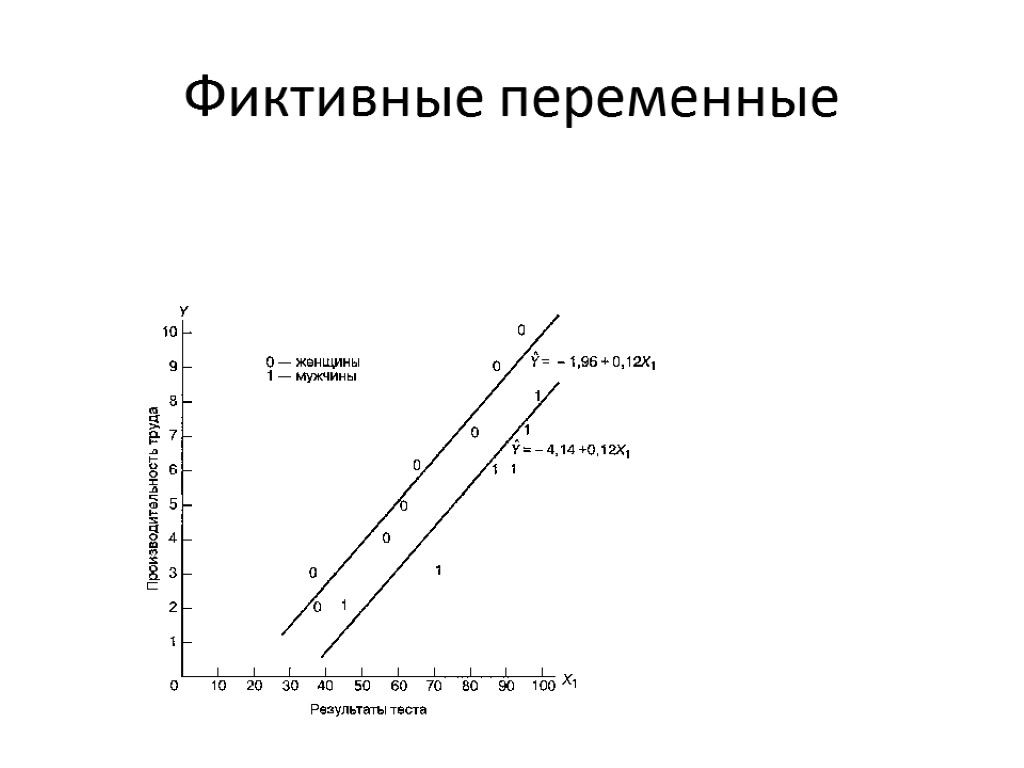
 Фиктивные переменные Фиктивные, или индикаторные, переменные используются для определения взаимосвязи между качественными независимыми переменными и зависимой переменной
Фиктивные переменные Фиктивные, или индикаторные, переменные используются для определения взаимосвязи между качественными независимыми переменными и зависимой переменной
 Фиктивные переменные
Фиктивные переменные
 Фиктивные переменные
Фиктивные переменные
 Фиктивные переменные
Фиктивные переменные
 Применение в менеджменте Маркетинг – вывод нового товара на рынок Агрономы – урожайность Медики – давление крови Менеджеры по персоналу – уровень заработной платы Менеджеры по рекламе – изменение мнения покупателей Руководство компаний – месторасположение розничных магазинов
Применение в менеджменте Маркетинг – вывод нового товара на рынок Агрономы – урожайность Медики – давление крови Менеджеры по персоналу – уровень заработной платы Менеджеры по рекламе – изменение мнения покупателей Руководство компаний – месторасположение розничных магазинов
 Многомерный регрессионный анализ Мультиколлинеарность Выбор «наилучшего» уравнения регрессии Анализ всех возможных регрессий Пошаговая регрессия
Многомерный регрессионный анализ Мультиколлинеарность Выбор «наилучшего» уравнения регрессии Анализ всех возможных регрессий Пошаговая регрессия
 Мультиколлинеарность Стоимость дома Год строительства Жилая площадь Кол-во комнат Кол-во продаваемых домов Неточная линейная зависимость – неустойчивость полученных оценок Рассчитанные величины больше ожидаемых Неверный знак отдельных коэффициентов Значимость регрессии по F-тесту при незначимых t-статистиках отдельных коэффициентов
Мультиколлинеарность Стоимость дома Год строительства Жилая площадь Кол-во комнат Кол-во продаваемых домов Неточная линейная зависимость – неустойчивость полученных оценок Рассчитанные величины больше ожидаемых Неверный знак отдельных коэффициентов Значимость регрессии по F-тесту при незначимых t-статистиках отдельных коэффициентов
 Мультиколлинеарность Мультиколлинеарность –линейная зависимость между двумя или более независимыми переменными Степень мультиколлениарности определяется фактором роста дисперсии - коэффициент детерминации из регрессии j-й независимой переменной по оставшимся (к-1) независимым переменным VIF близко к 1 – нет проблемы мультиколлинеарности больше 1- оценка коэффициента при этой независимой переменной неустойчива
Мультиколлинеарность Мультиколлинеарность –линейная зависимость между двумя или более независимыми переменными Степень мультиколлениарности определяется фактором роста дисперсии - коэффициент детерминации из регрессии j-й независимой переменной по оставшимся (к-1) независимым переменным VIF близко к 1 – нет проблемы мультиколлинеарности больше 1- оценка коэффициента при этой независимой переменной неустойчива
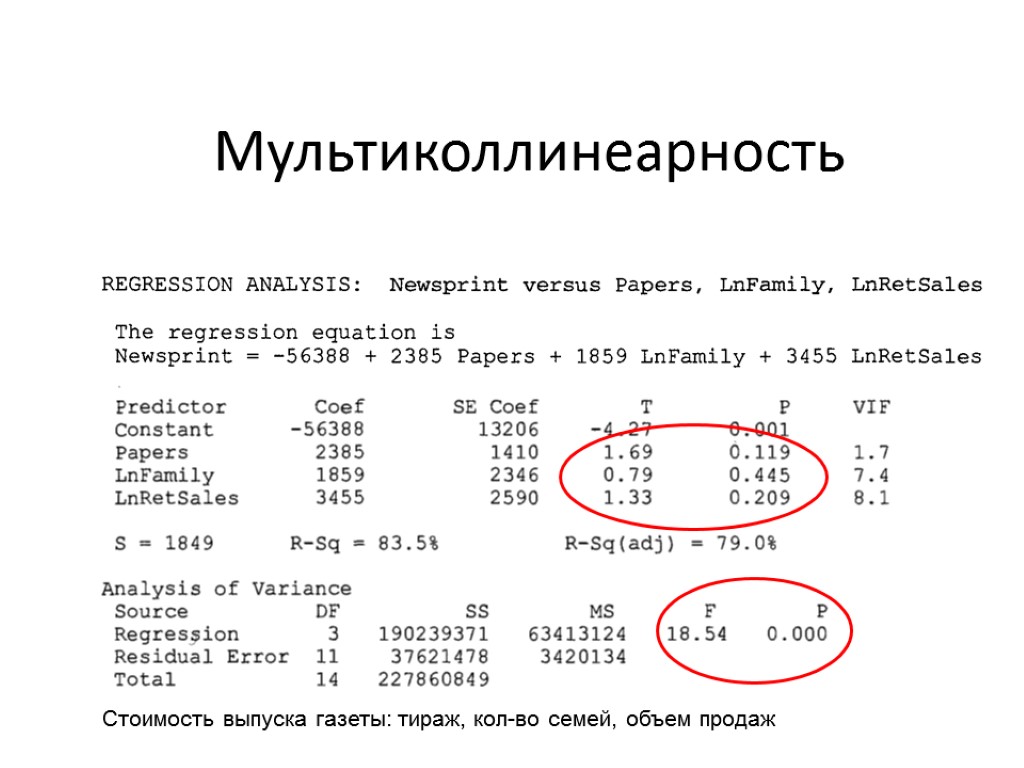
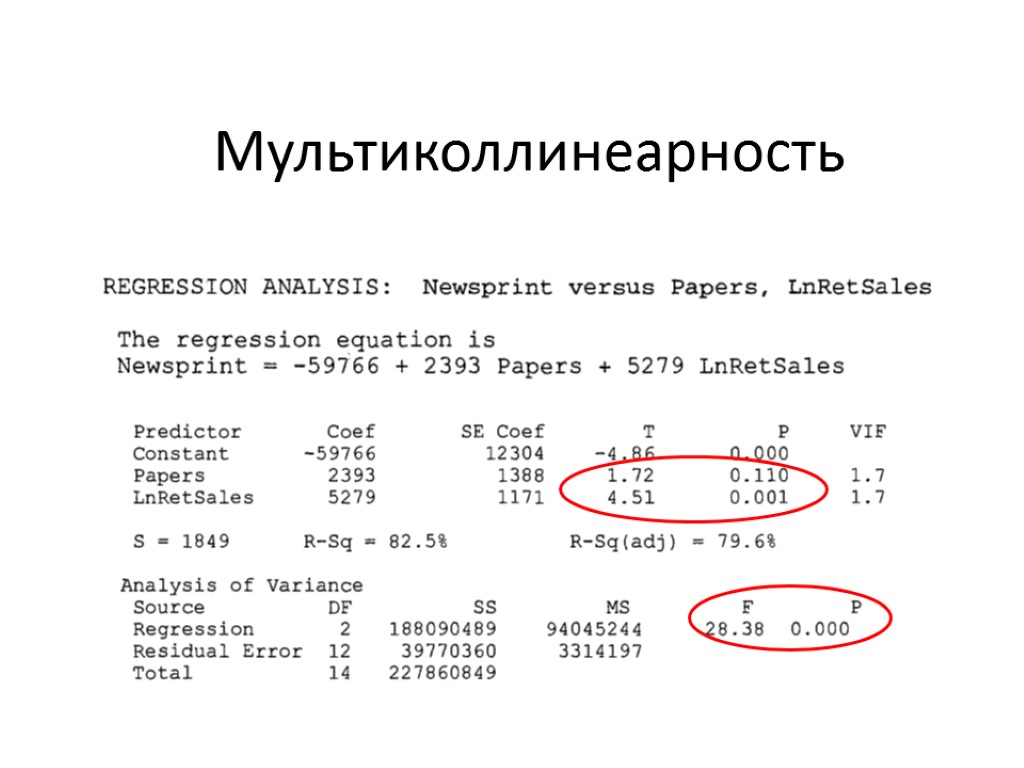
 Мультиколлинеарность Стоимость выпуска газеты: тираж, кол-во семей, объем продаж
Мультиколлинеарность Стоимость выпуска газеты: тираж, кол-во семей, объем продаж
 Мультиколлинеарность
Мультиколлинеарность
 Мультиколлинеарность При наличии в модели мультиколлинеарности для оценки эффекта одной отдельно взятой независимой переменной можно: Использовать метод, отличный от метода наименьших квадратов Найти и удалить из набора данных одну или более избыточных независимых переменных Представить зависимую переменную Y как линейную комбинацию некоррелирующих между собой независимых переменных Х Тщательно отобрать независимые переменные в начале исследования Создать новые переменные Х посредством масштабирования (нулевое среднее значение и одно и то же выборочное среднеквадратичное отклонение)
Мультиколлинеарность При наличии в модели мультиколлинеарности для оценки эффекта одной отдельно взятой независимой переменной можно: Использовать метод, отличный от метода наименьших квадратов Найти и удалить из набора данных одну или более избыточных независимых переменных Представить зависимую переменную Y как линейную комбинацию некоррелирующих между собой независимых переменных Х Тщательно отобрать независимые переменные в начале исследования Создать новые переменные Х посредством масштабирования (нулевое среднее значение и одно и то же выборочное среднеквадратичное отклонение)
 Выбор «наилучшего» уравнения регрессии Определение набора возможных независимых переменных Отбор переменных, неадекватных для данному случаю (например, при значительных ошибках измерения; недоступности данных; высокой их стоимости) Сокращение списка независимых переменных (нет «наилучшего» набора переменных, процесс отбора субъективен)
Выбор «наилучшего» уравнения регрессии Определение набора возможных независимых переменных Отбор переменных, неадекватных для данному случаю (например, при значительных ошибках измерения; недоступности данных; высокой их стоимости) Сокращение списка независимых переменных (нет «наилучшего» набора переменных, процесс отбора субъективен)
 Выбор «наилучшего» уравнения регрессии
Выбор «наилучшего» уравнения регрессии
 Выбор «наилучшего» уравнения регрессии
Выбор «наилучшего» уравнения регрессии
 Выбор «наилучшего» уравнения регрессии 1 шаг – изучение корреляционной матрицы 2 шаг – анализ всех возможных регрессий или пошаговая регрессия
Выбор «наилучшего» уравнения регрессии 1 шаг – изучение корреляционной матрицы 2 шаг – анализ всех возможных регрессий или пошаговая регрессия
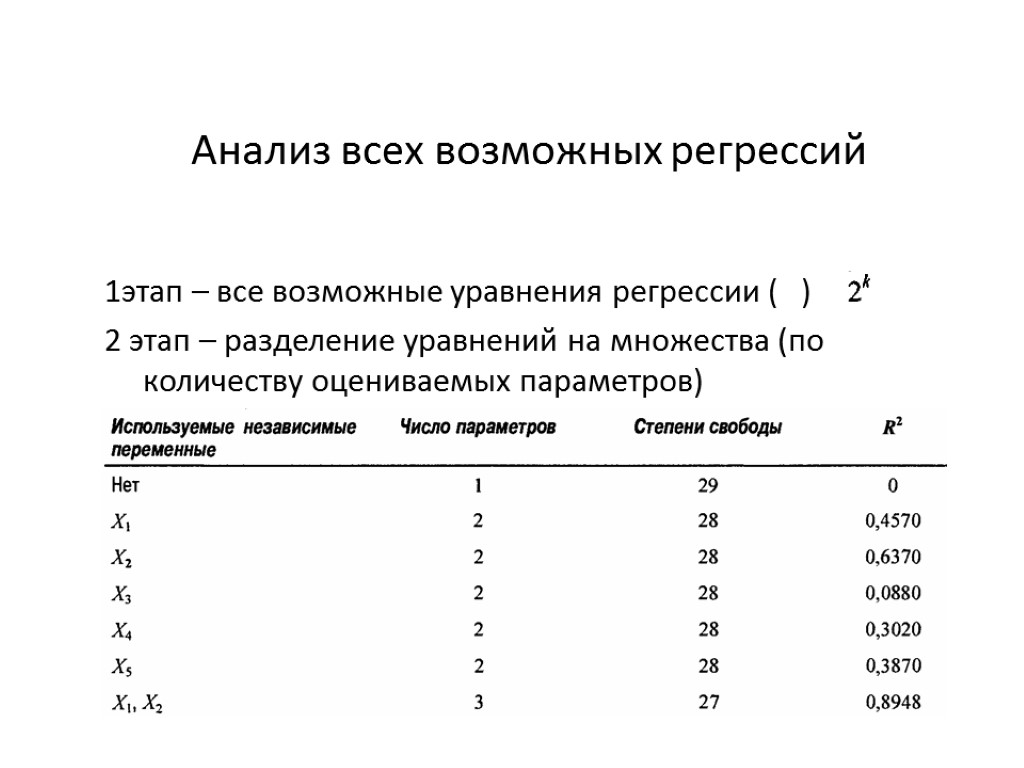
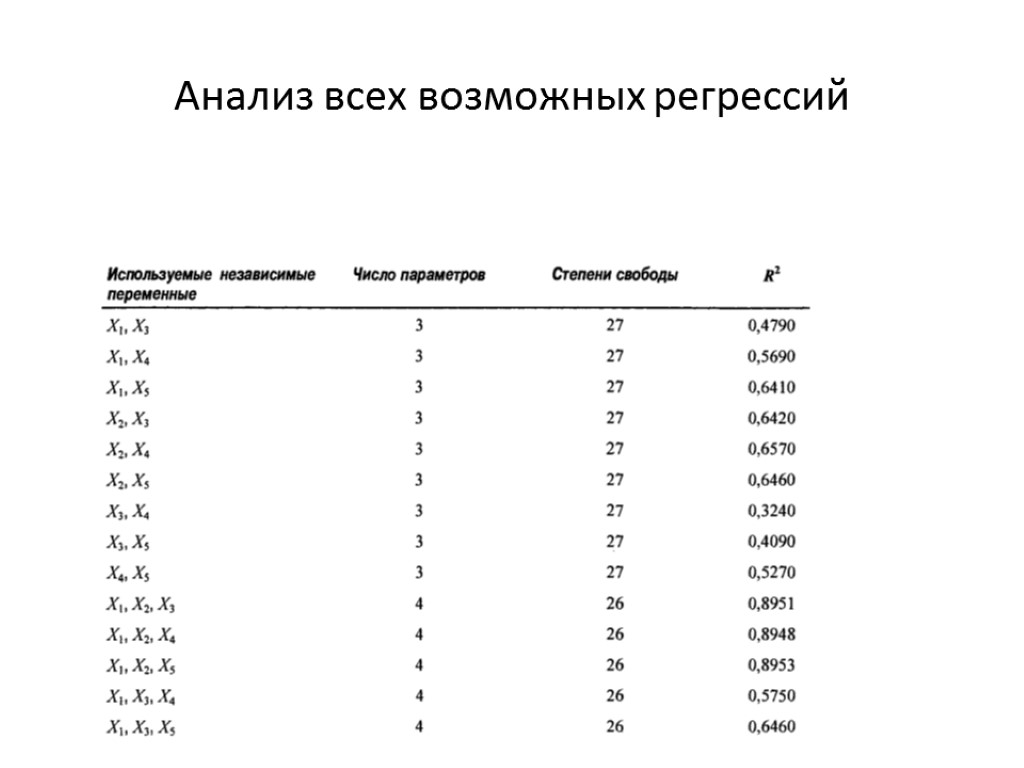
 Анализ всех возможных регрессий 1этап – все возможные уравнения регрессии ( ) 2 этап – разделение уравнений на множества (по количеству оцениваемых параметров)
Анализ всех возможных регрессий 1этап – все возможные уравнения регрессии ( ) 2 этап – разделение уравнений на множества (по количеству оцениваемых параметров)
 Анализ всех возможных регрессий
Анализ всех возможных регрессий
 Анализ всех возможных регрессий
Анализ всех возможных регрессий
 Анализ всех возможных регрессий 3 этап – выбор наилучшей независимой переменной (или переменных) из каждой группы с определенным числом параметров
Анализ всех возможных регрессий 3 этап – выбор наилучшей независимой переменной (или переменных) из каждой группы с определенным числом параметров
 Анализ всех возможных регрессий 4 этап – выбор наилучшего уравнения Желательно иметь наибольшее из возможных значений показателя детерминации, НО максимально простое уравнение регрессии Это уравнение объясняет 89,48% вариации переменной Y
Анализ всех возможных регрессий 4 этап – выбор наилучшего уравнения Желательно иметь наибольшее из возможных значений показателя детерминации, НО максимально простое уравнение регрессии Это уравнение объясняет 89,48% вариации переменной Y
 Пошаговая регрессия Процедура пошаговой регрессии предусматривает добавление в уравнение отдельных независимых переменных, по одной переменной на каждом этапе 1. Рассматриваются все возможные простые регрессии (наибольшая корреляция с зависимой переменной) 2. Следующая вводимая переменная должна привносить наибольший вклад в регрессионную сумму квадратов (F для включения) 3. Проверка уравнения (проверка на значимость независимой переменной на уровне 5%) , F=4 – критерий для включения или исключения 4. Этапы 2 и 3 повторяются, пока все возможные добавления не окажутся незначимыми, а все возможные удаления – значимыми Результат пошаговой регрессии – регрессионная модель, содержащая только независимые переменные с величинами t, значимыми на указанном уровне
Пошаговая регрессия Процедура пошаговой регрессии предусматривает добавление в уравнение отдельных независимых переменных, по одной переменной на каждом этапе 1. Рассматриваются все возможные простые регрессии (наибольшая корреляция с зависимой переменной) 2. Следующая вводимая переменная должна привносить наибольший вклад в регрессионную сумму квадратов (F для включения) 3. Проверка уравнения (проверка на значимость независимой переменной на уровне 5%) , F=4 – критерий для включения или исключения 4. Этапы 2 и 3 повторяются, пока все возможные добавления не окажутся незначимыми, а все возможные удаления – значимыми Результат пошаговой регрессии – регрессионная модель, содержащая только независимые переменные с величинами t, значимыми на указанном уровне
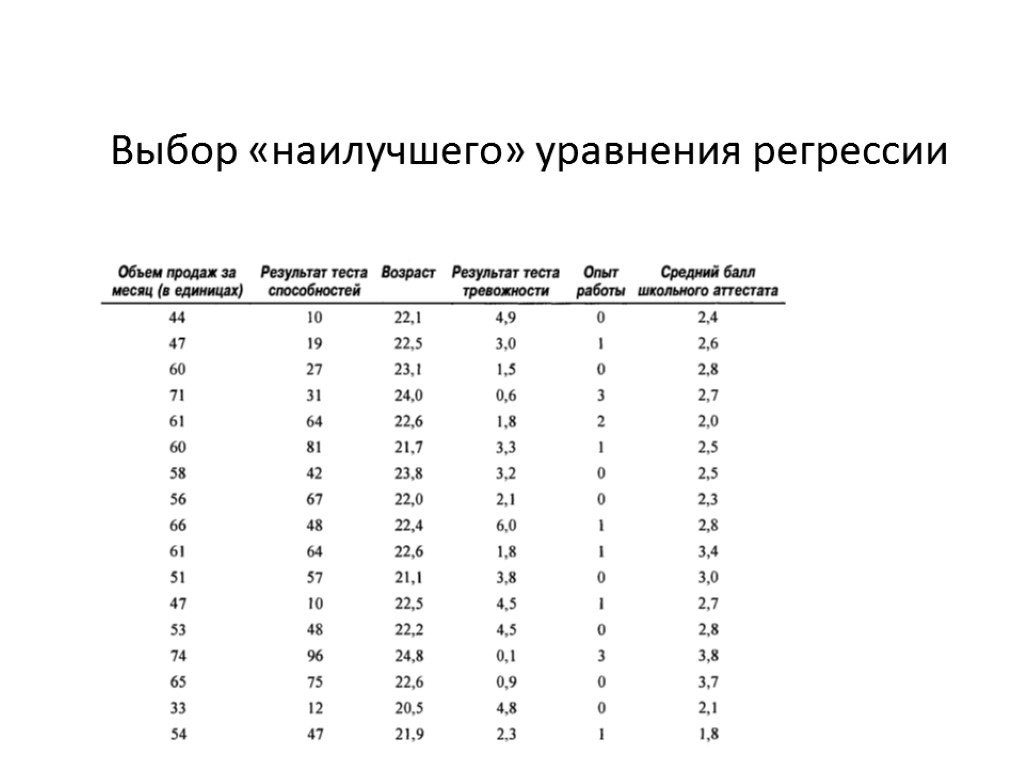
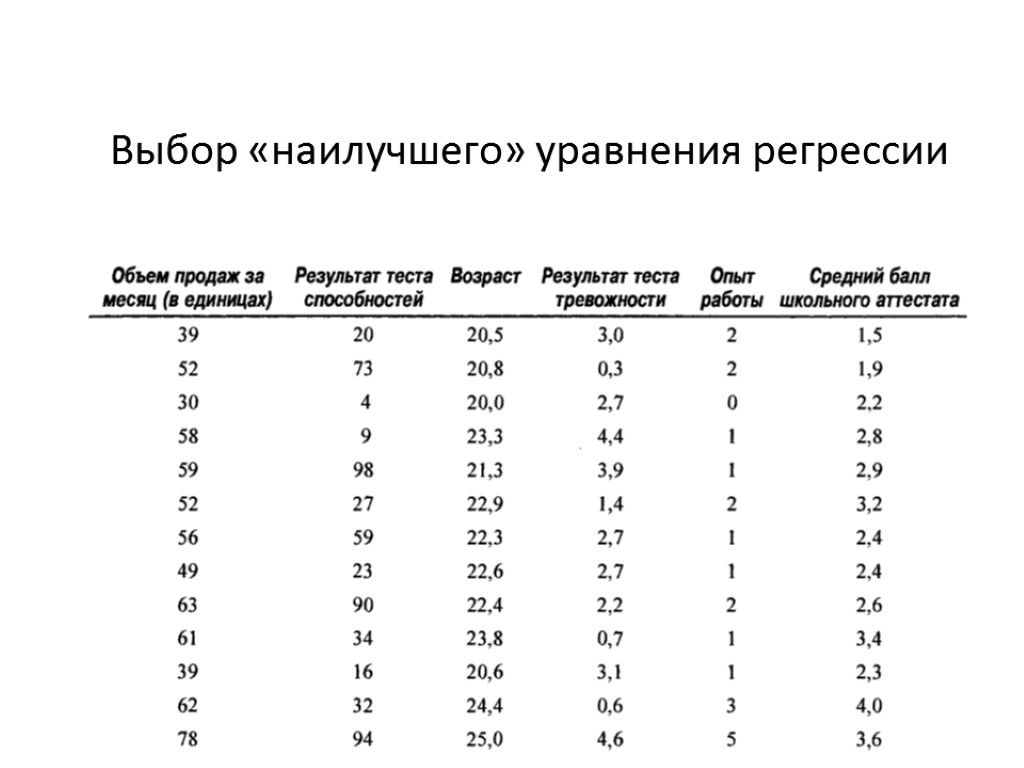
 Пошаговая регрессия Пример Первая переменная – возраст Вторая переменная – результат теста способностей Тест на тревожность не имеет тесной связи с объемом продаж Потенциально хорошие переменные опыта работы и среднего балла совместно с переменной возраста создают проблему мильтиколлинеарности
Пошаговая регрессия Пример Первая переменная – возраст Вторая переменная – результат теста способностей Тест на тревожность не имеет тесной связи с объемом продаж Потенциально хорошие переменные опыта работы и среднего балла совместно с переменной возраста создают проблему мильтиколлинеарности

