Регрессионные модели с переменной структурой ФУНКЦИЯ СПРОСА

Регрессионные модели с переменной структурой

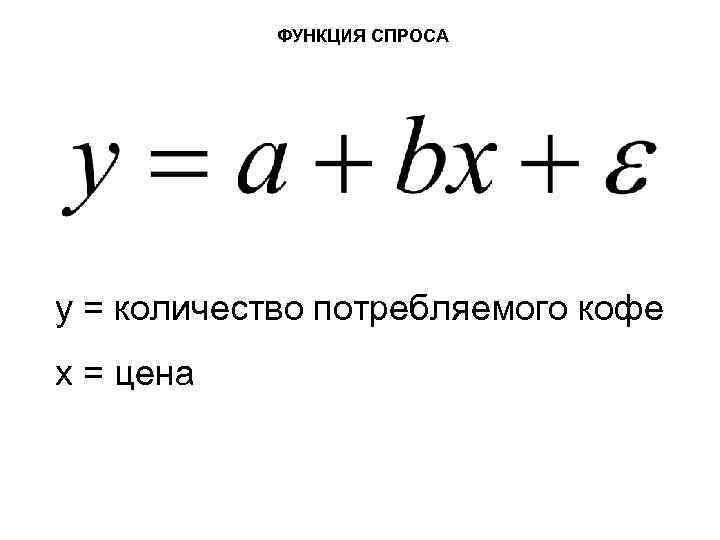ФУНКЦИЯ СПРОСА y = количество потребляемого кофе x = цена

Мужчины Женщины различны но сила влияния x на y может быть одинаковой, то есть

фиктивные переменные

Мужчины Женщины Различие потребления вызваны различием свободных членов уравнения регрессии

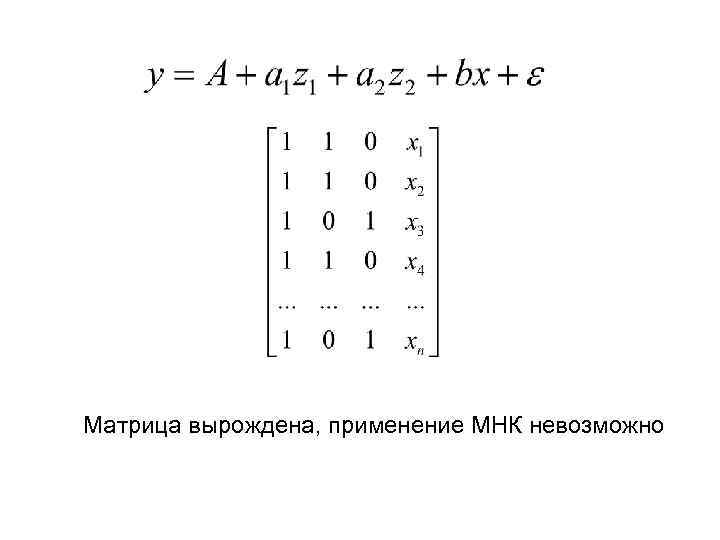Матрица вырождена, применение МНК невозможно

=1 Мужчины =0 Женщины различия в уровне потребления определяются в различии свободных членов и

Потребление для различных социальных и возрастных групп населения экономические (количественные) переменные

Цены на двухкомнатные квартиры

Регрессия на фиктивных переменных Модель заработной платы рабочих по регионам страны . . . . .

СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Система независимых уравнений • каждое уравнение может рассматриваться самостоятельно • для нахождения параметров используется МНК • в каждом уравнении присутствует величина случайной ошибки

Система рекурсивных уравнений • каждое уравнение может рассматриваться самостоятельно • для нахождения параметров используется МНК • в каждом уравнении присутствует величина случайной ошибки

Система взаимозависимых уравнений Система совместных одновременных переменных / Структурная форма модели содержит: Эндогенные переменные – зависимые переменные, число которых равно числу уравнений (y) Экзогенные переменные – предопределенные переменные, влияющие на эндогенные переменные, но независящие от них (x) Лаговые переменные (могут рассматриваться в качестве экзогенных) – значения эндогенных переменных за предшествующий период времени

Система взаимозависимых уравнений Система совместных одновременных переменных / Структурная форма модели • каждое уравнение не может рассматриваться самостоятельно • для нахождения параметров не используется МНК • все переменные выражены в отклонениях от среднего, т. е. по значениями x и y понимается

Приведенная форма модели • система независимых уравнений • оценка параметров по МНК • коэффициенты – нелинейные функции коэффициентов структурной формы модели

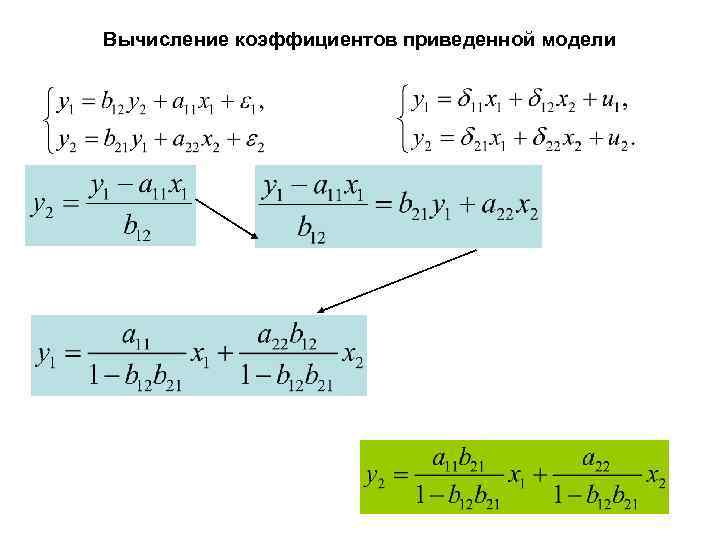Вычисление коэффициентов приведенной модели

Вычисление коэффициентов приведенной модели

Идентификация модели Идентификация – это единственность соответствия между приведенной и структурной формами модели Проблема: Количество параметров структурной формы модели Количество параметров приведенной формы модели Возможные решения: • предположить, что некоторые структурные коэффициенты равны нулю (слабая связь признаков с эндогенной переменной) • приравнять некоторые структурные коэффициенты (предположение о равном воздействие на эндогенную переменную)

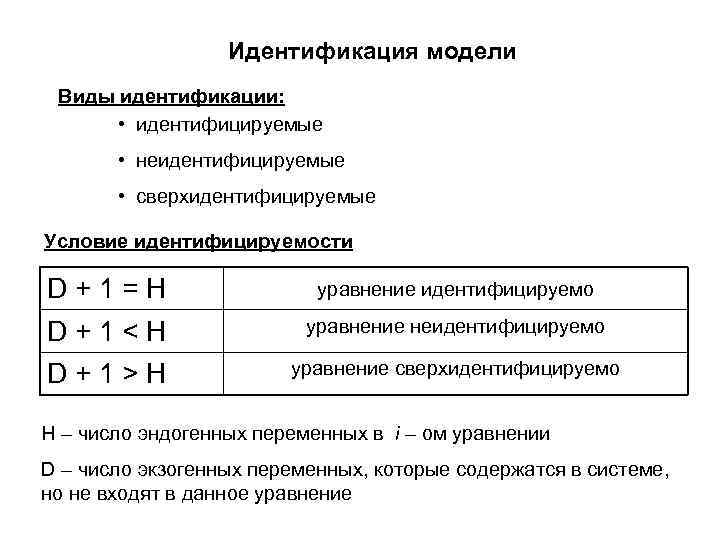Идентификация модели Виды идентификации: • идентифицируемые • неидентифицируемые • сверхидентифицируемые Условие идентифицируемости D+1=H уравнение идентифицируемо D+1H уравнение сверхидентифицируемо H – число эндогенных переменных в i – ом уравнении D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение

ПРИМЕР где Сt - расходы на потребление в период t, Yt – совокупный доход в период t, I t – инвестиции в период t, rt – процентная ставка в период t, Mt – денежная масса в период t, Gt – государственные расходы в период t, Ct-1 – расходы на потребление в период t-1, I t-1 инвестиции в период t-1. первое уравнение – функция потребления, второе уравнение – функция инвестиций, третье уравнение – функция денежного рынка, четвертое уравнение – тождество дохода.

Проверка условий идентификации уравнение сверхиденфицируемо Представляет собой тождество. Идентификация не требуется

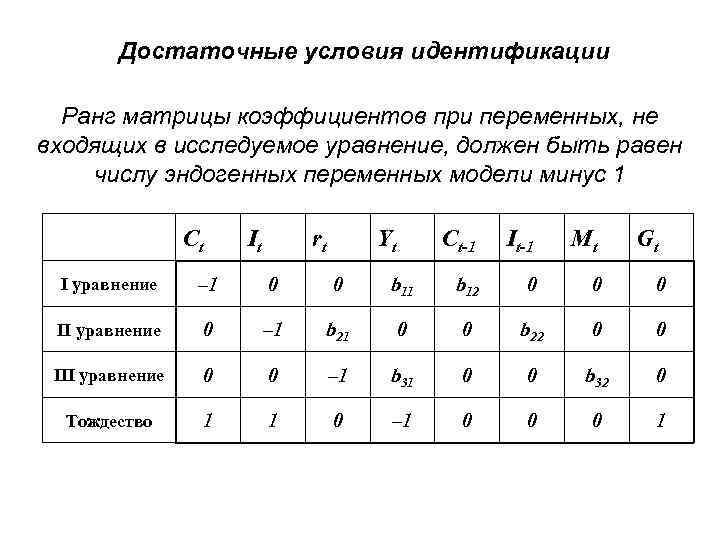Достаточные условия идентификации Ранг матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, должен быть равен числу эндогенных переменных модели минус 1 Сt It rt Yt Ct-1 It-1 Mt Gt I уравнение – 1 0 0 b 11 b 12 0 0 0 II уравнение 0 – 1 b 21 0 0 b 22 0 0 III уравнение 0 0 – 1 b 31 0 0 b 32 0 Тождество 1 1 0 – 1 0 0 0 1

Достаточные условия идентификации Первое уравнение It rt It-1 Mt Gt II уравнение – 1 b 22 0 0 III уравнение 0 – 1 0 b 32 0 Тождество 1 0 0 0 1 Достаточное условие выполняется

Достаточные условия идентификации Второе уравнение Сt Yt Ct-1 Mt Gt I уравнение – 1 b 12 0 0 III уравнение 0 b 31 0 b 32 0 Тождество 1 – 1 0 0 1 Достаточное условие выполняется

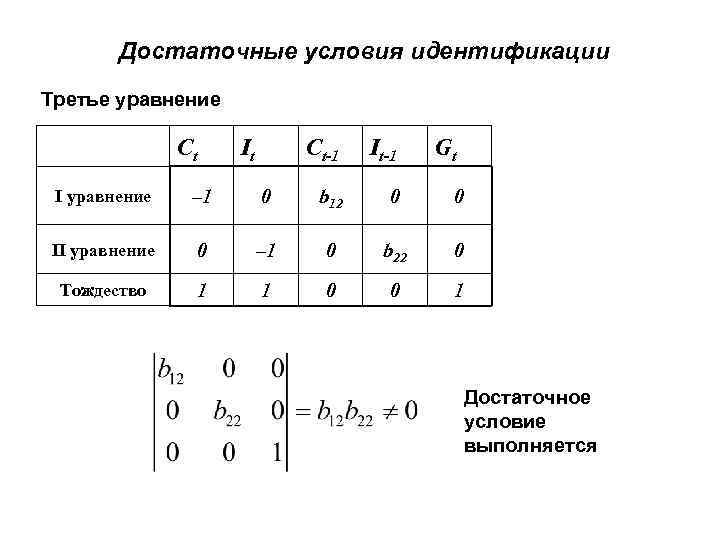Достаточные условия идентификации Третье уравнение Сt It Ct-1 It-1 Gt I уравнение – 1 0 b 12 0 0 II уравнение 0 – 1 0 b 22 0 Тождество 1 1 0 0 1 Достаточное условие выполняется

Приведенная форма модели