РЕГРЕССИОННЫЕ ЭКСПЕРИМЕНТЫ. ОРТОГОНАЛЬНОЕ И РОТАТАБЕЛЬНОЕ ПЛАНИРОВАНИЕ ЦЕЛЬ: Изучить методы построения планов первого и второго порядков, их свойств, провести эксперименты и регрессионный анализ результатов наблюдений
Полный факторный эксперимент Ключевые слова: фактор, активный эксперимент, матрица плана, уровень фактора, линейная регрессия, рандомизация, критерий Стьюдента, критерий Фишера. х1 х2. xn y
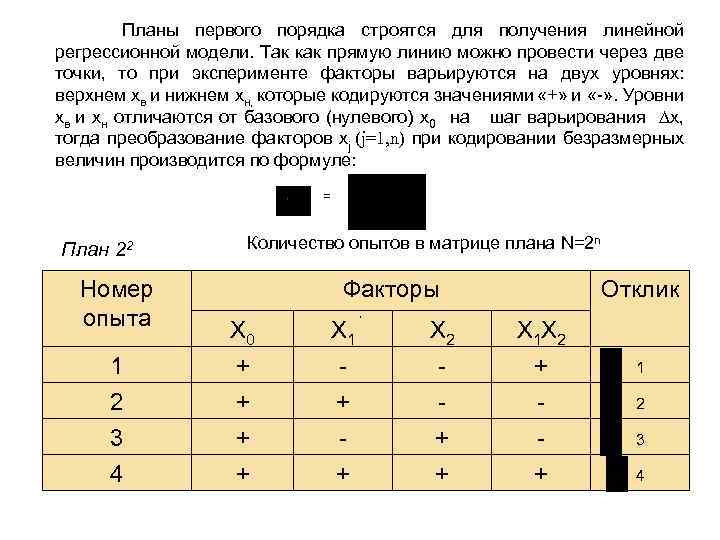
Планы первого порядка строятся для получения линейной регрессионной модели. Так как прямую линию можно провести через две точки, то при эксперименте факторы варьируются на двух уровнях: верхнем хв и нижнем хн, которые кодируются значениями «+» и «-» . Уровни хв и хн отличаются от базового (нулевого) х0 на шаг варьирования х, тогда преобразование факторов хj (j=1, n) при кодировании безразмерных величин производится по формуле: = План 22 Номер опыта Количество опытов в матрице плана N=2 n Факторы 1 2 X 0 + + X 1 + 3 4 + + + , Отклик X 2 - X 1 X 2 + - + + + 1 2 3 4
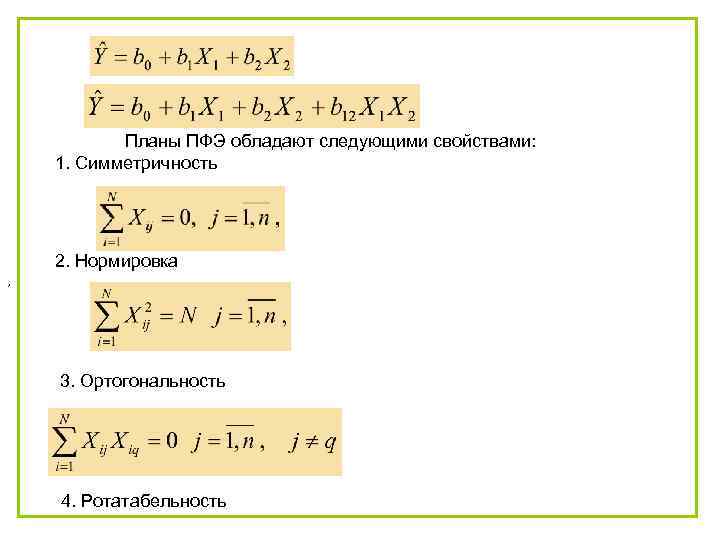
Планы ПФЭ обладают следующими свойствами: 1. Симметричность 2. Нормировка , 3. Ортогональность 4. Ротатабельность
Обработка результатов ПФЭ 1. проверка гипотезы об однородности дисперсий Si 2 – выборочная дисперсия выходной величины y по i-й строке матрицы планирования, полученная из m параллельных опытов: Yig – значение для i-той строки и g-ного опыта. Если вычисленные значения F и G окажутся меньше табличных, соответственно Fтабл (α, m-1) и Gтабл (α, m-1, N), то с вероятностью P=1 -α гипотеза об однородности дисперсий принимается.
2. Оценки коэффициентов уравнения регрессии 3. Гипотеза о статистической значимости коэффициентов регрессии t-критерий Стьюдента: к - число оцениваемых коэффициентов; Sb 2 - оценка дисперсии ошибки определения коэффициента bj; Sy 2 - оценка дисперсии воспроизводимости = Если tj , будет больше tтабл (α, N(m-1))), bj статистически значим
4. Проверка гипотезы об адекватности математического описания на основе критерия Фишера: S 2 аd – оценка дисперсии адекватности Yi – значение отклика, вычисленное по I – ой строке матрицы плана Если вычисленное значение f окажeтся меньше табличного, соответственно Fтабл (α, N-K, N(m-1)) то с вероятностью P=1 -α гипотеза об адекватности математического описания принимается. 2 1 6 4 9 5 1 8 7 3
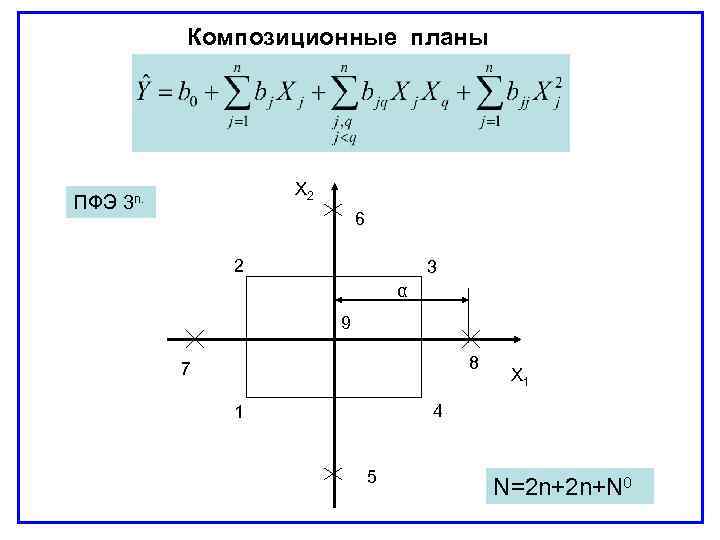
Композиционные планы ПФЭ Х 2 3 n. 6 2 3 α 9 8 7 Х 1 4 1 5 N=2 n+2 n+N 0
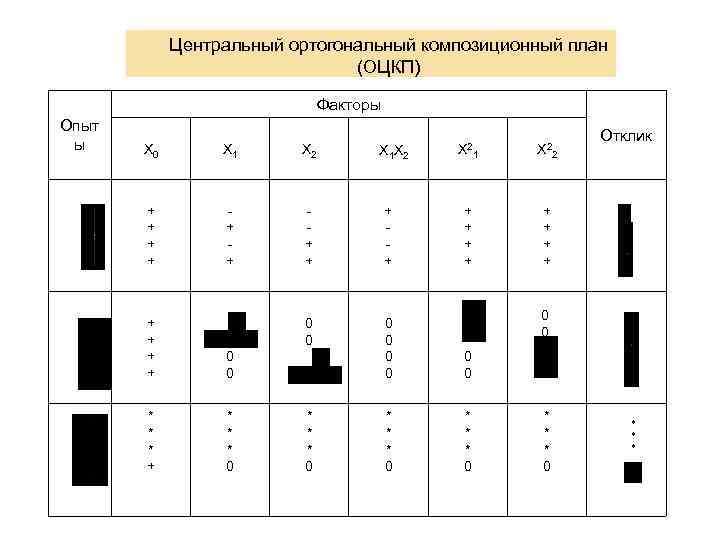
Центральный ортогональный композиционный план (ОЦКП) Факторы Опыт ы X 0 X 1 X 2 + + + + + 0 0 0 * * * + * * * 0 X 21 X 22 + + Отклик 0 0 + + X 1 X 2 + + 0 0 * * *
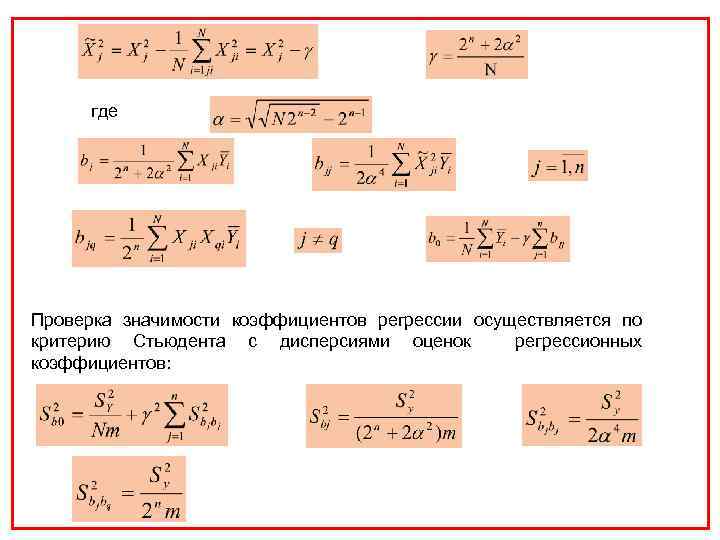
где Проверка значимости коэффициентов регрессии осуществляется по критерию Стьюдента с дисперсиями оценок регрессионных коэффициентов: .
Дробный факторный эксперимент (n > 6) ДФЭ 23 -1. Здесь n = 3, к =1, N=23 -1=4
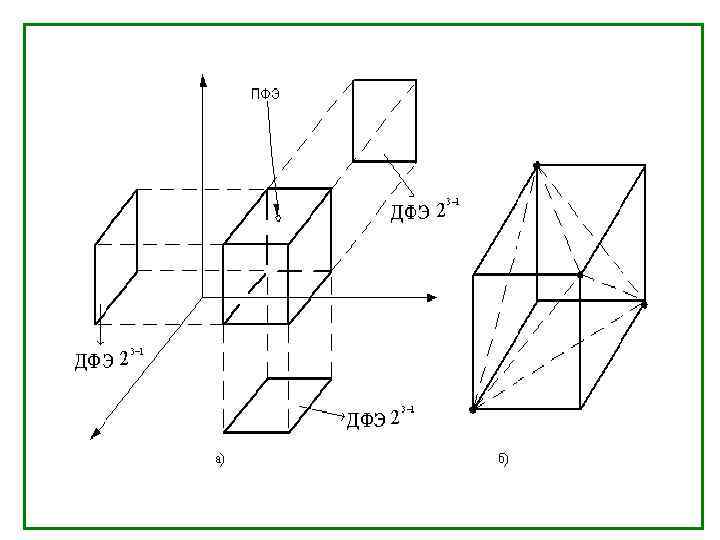
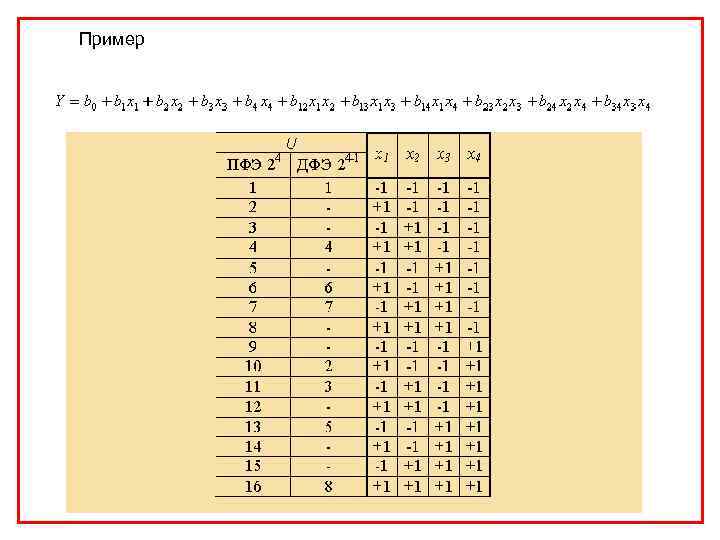
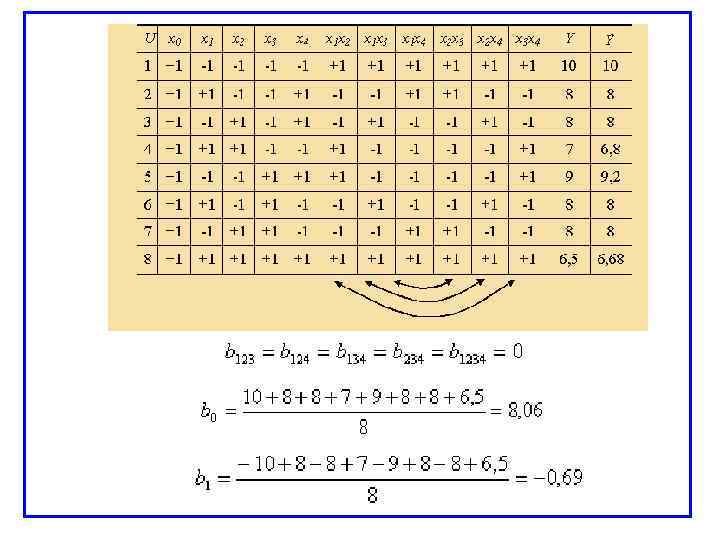
Пример
Скачать презентацию РЕГРЕССИОННЫЕ ЭКСПЕРИМЕНТЫ ОРТОГОНАЛЬНОЕ И РОТАТАБЕЛЬНОЕ ПЛАНИРОВАНИЕ ЦЕЛЬ Изучить
планирование эксперимента.ppt