Regression Verification Proving the equivalence of similar programs

Regression Verification: Proving the equivalence of similar programs Benny Godlin Ofer Strichman Technion, Haifa, Israel (This presentation is a subset of the invited cav’ 09 talk: ie. technion. ac. il/~ofers/presentations/rv 1. ppt) 1

Functional Verification n The main pillar of the grand challenge [H’ 03]. n Suppose we ignore completeness. n Still, there are two major problems: q q Specification Complexity 2

A more modest challenge: Regression Verification n Develop a method formally verifying the equivalence of two similar programs. n Pros: q q Default specification = earlier version. Computationally easier than functional verification. n n Ideally, the complexity should depend on the semantic difference between the programs, and not on their size. Cons: q Defines a weaker notion of correctness. 3

Our notion of equivalence Partial equivalence q n Executions of P 1 and P 2 on equal inputs n …which terminate, n result in equal outputs. Undecidable 5

Partial equivalence n Consider the call graphs: Side 2 … where A, B have: n n n B Side 1 q A same prototype no loops Prove partial equivalence of A, B q How shall we handle the recursion ? 6

Proving partial equivalence //in[A] A(. . . ) {. . . //in[call A] call A(. . . ); //out[call A]. . . } //out[A] A //in[B] B(. . . ) {. . . // in[call B] call B(. . . ); //out[call B]. . . } //out[B] B 7

Rule 1: Proving partial equivalence n n Q: How can a verification condition for the premise look like? A: Replace the recursive calls with calls to functions that q q n over-approximate A, B, and are partially equivalent by construction Natural candidates: Uninterpreted Functions 8

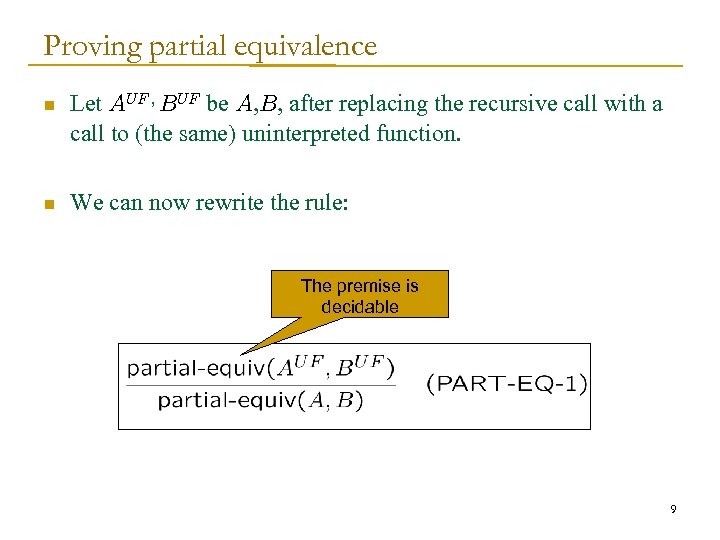Proving partial equivalence n Let AUF , BUF be A, B, after replacing the recursive call with a call to (the same) uninterpreted function. n We can now rewrite the rule: The premise is decidable 9

Using (PART-EQ-1): example unsigned gcd 1 UF (unsigned a, unsigned b) b) a, { unsigned g; if (b == 0) g = a; else { a = a % b; g = gcd 1(b, a); U } return g; g; } ? = unsigned gcd 2 UF (unsigned x, unsigned y) x, { unsigned z; z = x; if (y > 0) z = gcd 2(y, z % y); U } return z; z; } Transition functions Tgcd 1 Tgcd 2 Inputs a, b g x, y z Outputs 10

Rule 1: example Transition functions Tgcd 1 Tgcd 2 Inputs a, b x, y Outputs g z Equal inputs Equal outputs 11

Partial equivalence: Generalization n Assume: q q no loops; 1 -1 mapping map between the recursive functions of both sides n n Mapped functions have the same prototype Define: q For a function f, UF(f) is an uninterpreted function such that n f and UF(f) have the same prototype n (f, g) 2 map , UF(f) = UF(g). 12

Partial equivalence: Generalization n Definition: is called in A] 13

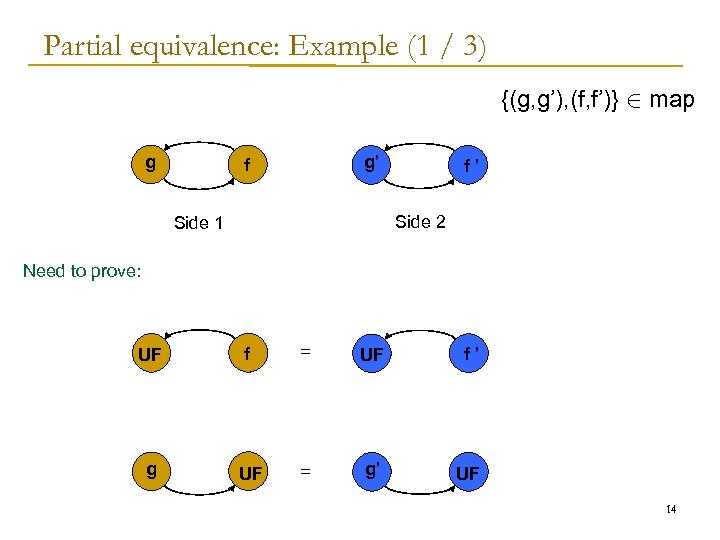Partial equivalence: Example (1 / 3) {(g, g’), (f, f’)} 2 map g g’ f f’ Side 2 Side 1 Need to prove: UF f = UF f’ g UF = g’ UF 14

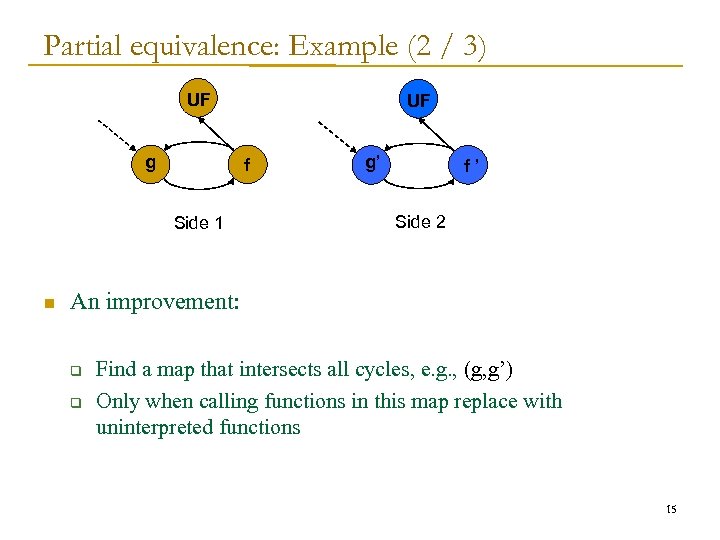Partial equivalence: Example (2 / 3) UF g f Side 1 n UF g’ f’ Side 2 An improvement: q q Find a map that intersects all cycles, e. g. , (g, g’) Only when calling functions in this map replace with uninterpreted functions 15

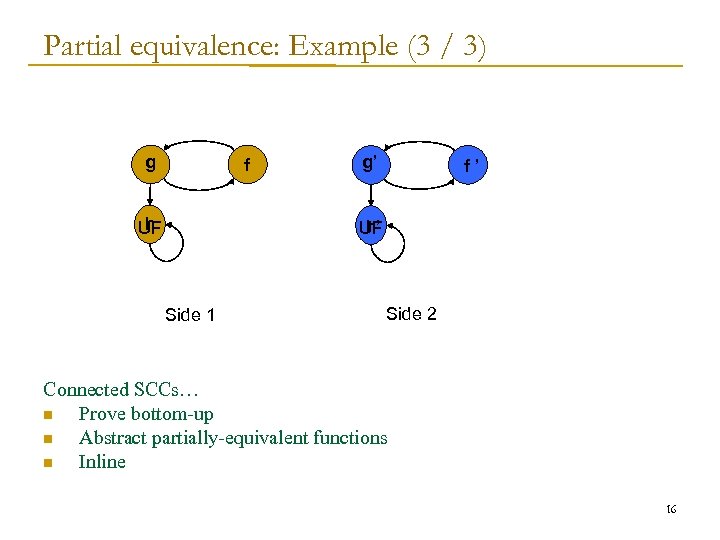Partial equivalence: Example (3 / 3) g f h UF g’ f’ h’ UF Side 1 Side 2 Connected SCCs… n Prove bottom-up n Abstract partially-equivalent functions n Inline 16

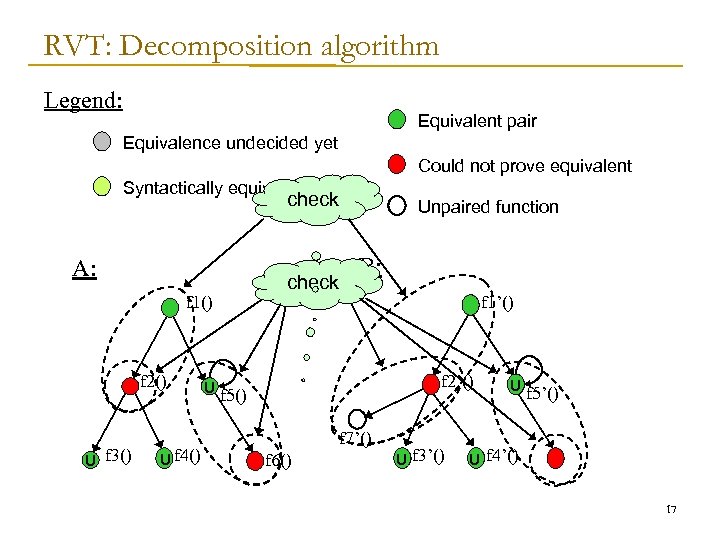RVT: Decomposition algorithm Legend: Equivalent pair Equivalence undecided yet Could not prove equivalent Syntactically equivalent pair check A: check f 1() f 2() U f 3() U f 4() U Unpaired function B: f 1’() f 2’() f 5() f 7’() f 6() U f 3’() U f 5’() U f 4’() 17

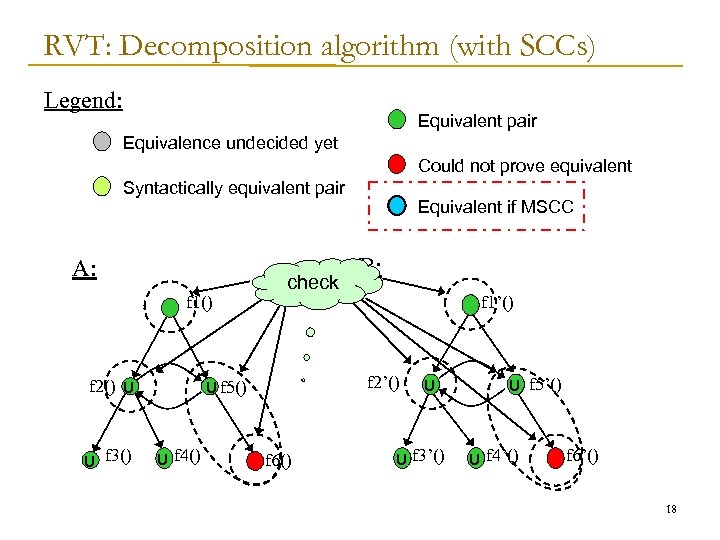RVT: Decomposition algorithm (with SCCs) Legend: Equivalent pair Equivalence undecided yet Could not prove equivalent Syntactically equivalent pair A: f 1() f 2() U U f 3() check B: f 1’() f 2’() U f 5() U U f 4() Equivalent if MSCC f 6() U U f 3’() U f 5’() U f 4’() f 6’() 18

The Regression Verification Tool (RVT) n Given two C programs: q loops recursive functions. q n Map functions, globals, etc. After that: q q Decompose to the granularity of pairs of functions Use a C verification engine (CBMC) to discharge 19

The Regression Verification Tool (RVT) n CBMC: a C bounded model checker by Daniel Kroening n Our use: q q q n No loops or recursion to unroll. . . Use “assume(…)” construct to enforce equal inputs. Use assert() to demand equal outputs. Uninterpreted functions are implemented as C functions: q Return consistent nondeterminisitic values. 20

The Regression Verification Tool (RVT) n The premise of (PART-EQ) requires comparing arguments. n What if these arguments are pointers ? n What our system does: q q Dynamic structures: creates an unrolled nondeterministic structure Arrays: attempts to find references to cells in the array. 21

RVT: User-defined equivalence specification n The user can define pairs of ‘checkpoints’: side 1: side 2: n In each side: q n update an array with the value of exp each time it reaches label and condition holds. Assert that when executed on the same input…, q … these arrays are equivalent. P 1: exp 1 = = P 2: exp’ 1 exp’ 2 . . . exp 2 = = . . . 22

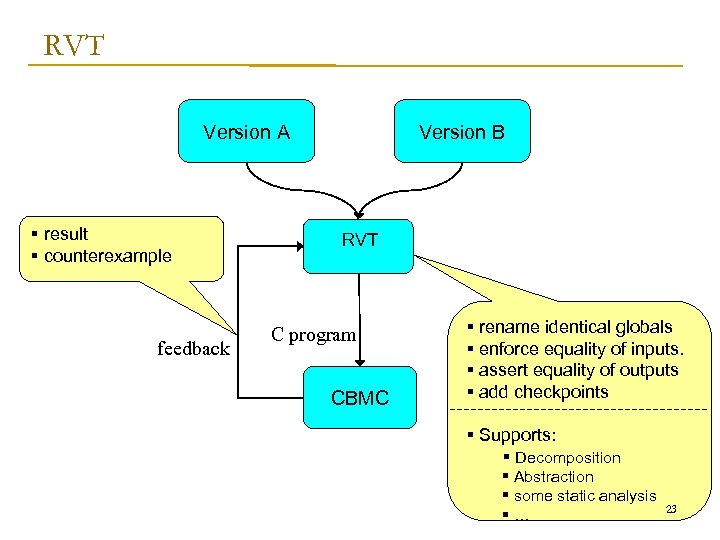RVT Version A § result § counterexample feedback Version B RVT C program CBMC § rename identical globals § enforce equality of inputs. § assert equality of outputs § add checkpoints § Supports: § Decomposition § Abstraction § some static analysis §… 23

24

RVT: Experiments We tested the Regression Verification Tool (RVT) with: n Automatically generated sizable programs with complex recursive structures and loops. n up-to thousands of lines of code n Limited-size industrial programs: q Parts of TCAS - Traffic Alert and Collision Avoidance System. q Core of Micro. C/OS - real-time kernel for embedded systems. q Matlab examples: parts of engine-fuel-injection simulation. 25

Testing RVT on programs: Conclusions n For equivalent programs, partial-equivalence checks were very fast: q n proving equivalence in minutes. For non-equivalent programs: q RVT attempts to prove partial-equivalence but fails n then RVT tries to prove k-equivalence 26

Summary n Regression verification is an important problem q q n A solution to this problem has a better chance to succeed in the industry than functional verification A grand challenge by its own right… Lots of future research. . . 27

More Challenges n Q 1: How can we generalize counterexamples ? n Q 2: What is the ideal gap between two versions of the same program, that makes Regression Verification most effective ? n Q 3: How can functional verification and equivalence verification benefit from each other ? 28

The end… n Thank you 29