Refinement and Transformations in Specware A progress report

Refinement and Transformations in Specware A progress report Alessandro Coglio, Kestrel Institute Stephen Westfold, Kestrel Institute Lambert Meertens, Utrecht University IFIP WG 2. 1 meeting, 京都市, Sep 2007 1

Specware • Specware is the “flagship” system of Kestrel Institute, developed over a sequence of years • The current release is Specware 4. 2 • Specware is a system that supports the correct-by-construction paradigm: start with a clear spec capturing the functional requirements as transparently as possible, and next massage it by provably correct refinement steps into an implementation IFIP WG 2. 1 meeting, 京都市, Sep 2007 2

KIDS versus Specware • KIDS (Kestrel Interactive Development System, Doug Smith, 1990) was designed for, and excelled in, transformational programming in the small • Specware was designed for system development in the large unfortunately, the initial designers paid scant attention to the convenience of doing the small steps • Recently, Kestrel has begun to address this IFIP WG 2. 1 meeting, 京都市, Sep 2007 3

Overview • What Specware already had: – – Specs, models, and refinement Metaslang Spec calculus Proof obligations • What is new: – Refinements refined – Transformations IFIP WG 2. 1 meeting, 京都市, Sep 2007 4

Specs spec op is. Monotonic? : (Nat Nat) Boolean def is. Monotonic? f = fa (x, y) (x y) (f x f y) op sq : (Nat | is. Monotonic? ) axiom sq. Distributes. Over. Times is fa (m, n) sq (m n) = (sq m) (sq n) endspec IFIP WG 2. 1 meeting, 京都市, Sep 2007 5

Models • A spec has zero or more models (mathematical “worlds” satisfying the spec) • A spec with no models is inconsistent (e. g. , one containing axiom foo is 0 = 1) • The spec on the previous slide has many models, since there are many monotonic functions of type N N that distribute over multiplication (e. g. , the identity function) IFIP WG 2. 1 meeting, 京都市, Sep 2007 6

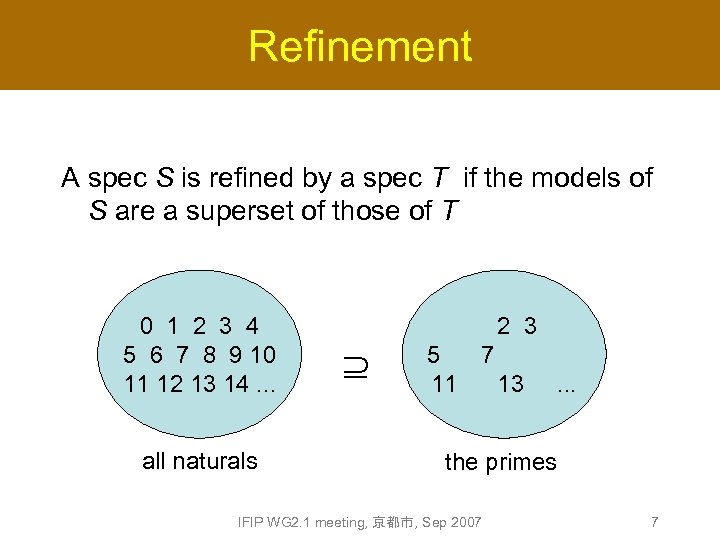Refinement A spec S is refined by a spec T if the models of S are a superset of those of T 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14. . . all naturals 2 3 5 7 11 13 . . . the primes IFIP WG 2. 1 meeting, 京都市, Sep 2007 7

Metaslang • Metaslang is the language of the Specware system • Metaslang is a typed higher-order language, comparable to ML or Haskell, but allowing “non-constructive” dictions and definitions (e. g. , fa and ex), and constraining the models by axioms. • Metaslang has constructs for defining and composing specs and refinements IFIP WG 2. 1 meeting, 京都市, Sep 2007 8

Spec calculus • Import. Specs can “import” other specs, which then implies that they refine the imported specs • Renaming. Types and ops declared in specs can be renamed; generally not a refinement • Substitution. If spec S = F(A) contains a subspec A, and we have a refinement R : A B, the notation S[R] stands for F(B), and S S[R] is again a refinement IFIP WG 2. 1 meeting, 京都市, Sep 2007 9

Proof obligations • Proof obligations can be engendered both by specs and by refinements • def n : Nat = 5206 9762 -5537 9178 requires a proof that the result of evaluating 5206 9762– 5537 9178 is nonnegative • A refinement of the spec introducing function sq to one defining def sq n = n n requires a proof that the function thus defined is monotonic and multiplicative IFIP WG 2. 1 meeting, 京都市, Sep 2007 10

Connections to provers • Generated proof obligations can currently be submitted to two theorem provers (after having been translated to the appropriate logic and language, if possible): – SNARK: an automated first-order prover – Isabelle/HOL: a higher-order prover • Proofs of discharged proof obligations can be recorded in specs (in a prover-dependent format) IFIP WG 2. 1 meeting, 京都市, Sep 2007 11

Two problems in practice • The notion of refinement is too strict, not making a distinction between auxiliary ops that are purely ancillary to formulating the requirements (e. g. is. Monotonic? ) and the “main” ops describing the “design object” • The mechanisms for creating refinements are too coarse — they are awkward for small steps — and thereby discourage exploration as well as modularity in proofs IFIP WG 2. 1 meeting, 京都市, Sep 2007 12

Observable ops • We introduce a distinction between “observable” ops and the rest • If a, b, and x are observable ops, the semantics of a spec can be given as the characteristic predicate of its set of models: a, b, x: P(a, b, x) • If, however, x is not observable but auxiliary, the semantics becomes: a, b: x: P(a, b, x) IFIP WG 2. 1 meeting, 京都市, Sep 2007 13

Refinement refined • If the semantics of spec S is given by: a, b: x: P(a, b, x) while that of T is given by: a, b: Q(a, b) and it is the case that: a, b: ( x: P(a, b, x)) Q(a, b) then S T is a valid refinement • Thus, auxiliary ops such as x may be “refined away” IFIP WG 2. 1 meeting, 京都市, Sep 2007 14

Transformations • The spec calculus has been extended by a new construct: transform S by {t 0, t 1, . . . } in which t 0, t 1, . . . are transformation steps • Transformation steps are meaning-preserving edit operations on the text of the spec • For example: replace expr by equivalent expr IFIP WG 2. 1 meeting, 京都市, Sep 2007 15

Some transformation steps • at N — focus on the definition of N • first, next, last, previous, widen — move focus • lr T — rewrite using equality of theorem T • unfold N — unfold definition of N • fold N — fold with definition of N • simplify(rules) — simplify using rules • eval — evaluate ground terms IFIP WG 2. 1 meeting, 京都市, Sep 2007 16

The Transformation Shell • The Transformation Shell is an interactive tool (actually functioning as a special mode of the normal Specware Shell) using which users can interactively issue “transformation commands” corresponding to transformation steps, and see each time the result • At the end of a session, the Transformation Shell produces a script in the form of a list of transformation steps IFIP WG 2. 1 meeting, 京都市, Sep 2007 17

Example script • An example of a script produced this way: Simplified. Spec = transform Refined. Spec by {at construct', unfold iso, lr if_pull, lr if_subst, Simp. Standard, at flip', simplify (unfold iso), move (first), lr if_pull, eval, lr if_pull, lr if_subst, Simp. Standard, lr if_swap} IFIP WG 2. 1 meeting, 京都市, Sep 2007 18

Candidate enhancements • Refinement libraries • On-the-spot introduction of new theorems needed for rewrites • Transformation “strategies” (Stratego) • User-defined transformation rules Such enhancements should be driven by need IFIP WG 2. 1 meeting, 京都市, Sep 2007 19

Conclusion • A relatively small effort has achieved a marked improvement in the practical usability of Specware • There is still room for further considerable improvements, much of which is still also achievable with relatively small efforts before the law of diminishing returns kicks in IFIP WG 2. 1 meeting, 京都市, Sep 2007 20