c0734058aa0fbc5492aea69c314893ae.ppt
- Количество слайдов: 23

Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Eduard C. Dragut University of Illinois at Chicago Ramon Lawrence University of British Columbia Okanagan ODBASE 2006, Montpellier, France

Talk Overview Ü Ü Ü Introduction Background ð Model and Mapping representation systems Proposed Mapping Representation System ð Ü Ü Invert and Compose operator definitions and properties Mappings Composition Experiment ð Estimate the quality of the proposed system E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 2

Introduction - Terminology Ü Models ð denote a representation of a domain in a formal language (e. g. , EER, Relational, Description Logic) ð has two components [Russell et al 2003] terminological (or metadata) Ø This is the focus of this work and talk. extensional Ü (i. e. facts or instances) Mappings ð describe how two models are related to each other E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 3

Introduction - Mappings Ü Ways to define mappings between models ð binary relationships ð mapping using a helper model ð [Bernstein et al. 2003] mapping as queries Ü called morphisms [Melnik et al 2003] or inter-schema correspondences [Popa et al. 2002] [Madhavan et al. 2003, Berstein et al. 2006] Our work falls in the class of the first two types of mappings. ð We call them metadata level mappings. They are not concerned with the instances of a model. E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 4

Introduction - Examples Ü Examples of models ð diagrams, interface definitions, database schemas, web site layouts, control flow, XML schemas Ü Applications of mappings ð mapping between XML schemas to drive message translation; ð schema and database integration; ð mapping between ontologies to help in the process of merging and alignment E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 5

Background - Mapping creation Ü Ü The creation will be rarely completely automated. General strategy is to semi-automatically build mappings ð use heuristics to generate matchings (e. g. name similarity) ð translate matches into formulas ð [Rahm and Bernstein 2001, Shvaiko and Euzenat 2005] (surveys) E. g. , Clio project [Popa et al. 2002] generate new mappings from existing mappings Composition Ø E. g, [Madhavan et al. 2003, Berstein et al. 2006] Invert Ø E. g, Ü [Fagin 2006] Semi-automatic tools can significantly speed up the process. E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 6

Background - Morphisms Ü Mapping: ð ð Ü is just a set of binary relations between the elements of two models is a set of pairs < l, r > Advantages/Disadvantages ð ð their expressiveness is enough for certain classes of problems and they exhibit certain mathematical properties [Melnik et al. 2003] main drawback assumes similarity to be transitive E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 7
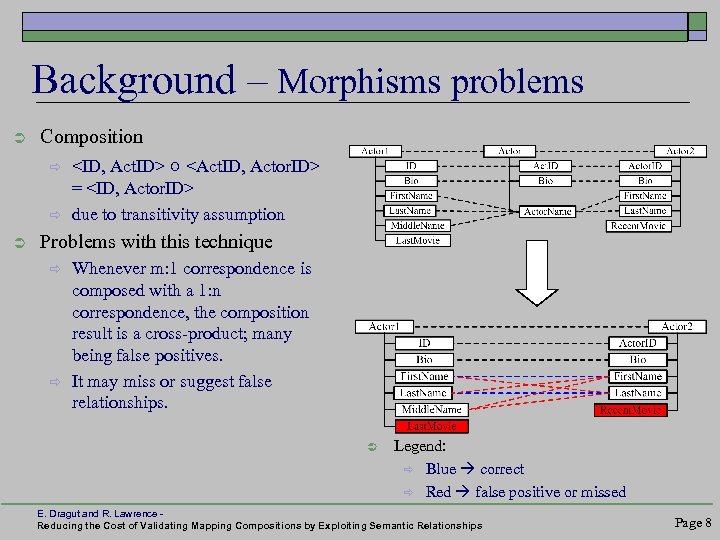
Background – Morphisms problems Ü Composition ð ð Ü <ID, Act. ID> ○ <Act. ID, Actor. ID> = <ID, Actor. ID> due to transitivity assumption Problems with this technique ð ð Whenever m: 1 correspondence is composed with a 1: n correspondence, the composition result is a cross-product; many being false positives. It may miss or suggest false relationships. Ü Legend: ð Blue correct ð Red false positive or missed E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 8
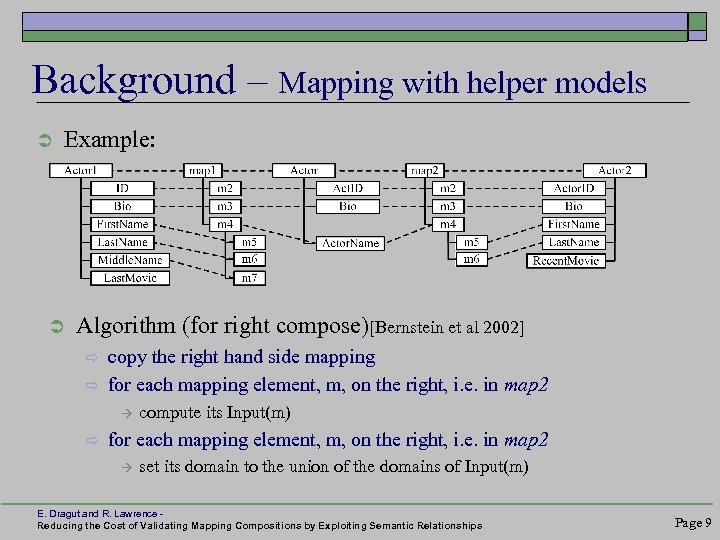
Background – Mapping with helper models Ü Example: Ü Algorithm (for right compose)[Bernstein et al 2002] ð ð copy the right hand side mapping for each mapping element, m, on the right, i. e. in map 2 ð compute its Input(m) for each mapping element, m, on the right, i. e. in map 2 set its domain to the union of the domains of Input(m) E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 9

Background – Mapping with helper models Ü Composition result Ü Problems with this technique ð It may miss or suggest false relationships. Ü Legend: ð Red missed relationships E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 10

The Objectives Ü The driving motivation ð ð Ü Provide a mapping representation at the metadata level combining the advantages of morphisms and mappings with helper models. ð ð Ü The need for a mapping definition subsuming the relationship kinds that the state of the art matching algorithms discover with high precision. Investigate to what extent a set of operations over this mapping definition can be defined. The former has good mathematical properties. The latter is more expressive. Provide a compose algorithm that exploits the semantic relationships within the mapping expression to produce correct semantic relationships whenever these can be determined automatically and to isolate those instances that require human intervention. E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 11

Proposed Mappings Representation Ü Model ð A model has similar expressiveness as an EER model and is consistent with the definition of model used in previous work on model management. [Bernstein et al 2002, Pottinger and Bernstein 2003] Ü Mapping Representation ð A mapping consists of a set of mapping elements, each mapping element is a directed, kinded binary relationship between a pair of elements not in the same model: Ü Triplets of form < m 1, type, m 2 >, type = {Is. A, AKind. Of, Has. A, Part. Of, =, Contains, Contained. By, Unknown, Complex} Comments ð Some of these types were introduced in other works. E. g, [Euzenat 2004, Giunchiglia et al. 2004, Pottinger and Bernstein 2003, Xu and Embley 2003, Wu et al. 2004] E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 12
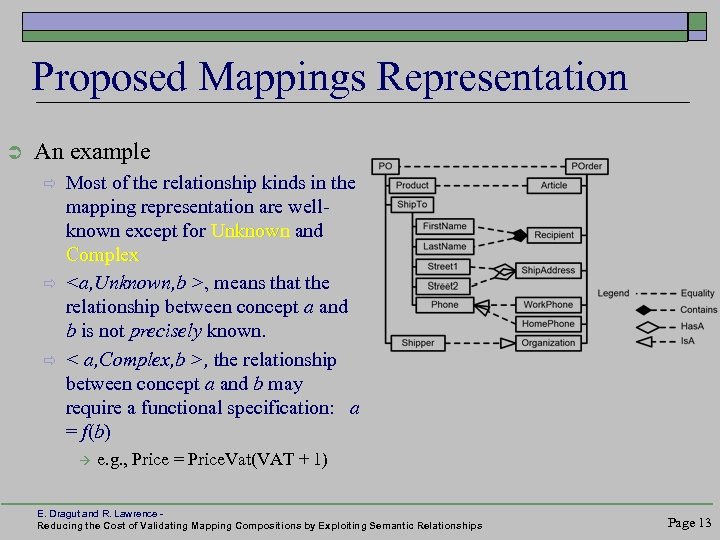
Proposed Mappings Representation Ü An example ð ð ð Most of the relationship kinds in the mapping representation are wellknown except for Unknown and Complex <a, Unknown, b >, means that the relationship between concept a and b is not precisely known. < a, Complex, b >, the relationship between concept a and b may require a functional specification: a = f(b) e. g. , Price = Price. Vat(VAT + 1) E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 13

Operators - Invert Ü Each of the relationship types introduced have well defined inversion properties: ð Ü Is. A inverted is AKind. Of, Has. A inverted is Part. Of, Contains inverted is Contained. By Definition [invert for mapping elements]: ð ð Consider m = < a, type, b >. Then its corresponding inverted mapping element, denoted m-1, is given by the following expression: < b, type-1, a> Mathematical form: < a, type, b >-1 = < b, type-1, a > Ü E. g. < a, Has. A, b >-1 = < b, Has. A-1, a > Definition [invert for mappings]: ð Given two models A and B and a mapping, map, between them, the invert of map denoted by map-1, is defined from B to A and its expression is given by: map-1 = {< b, type-1, a >| < a, type, b > map} E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 14

Operators - Compose Ü Composing two mappings involves defining a composition operation between the elements of the mappings (i. e. between triplets of form < a, type, b >) Ü Example ð <Home. Phone, Is. A, Phone> ○ <Phone, = , Telephone> = < Home. Phone, Is. A, Telephone> E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 15

Compose Properties Ü Remarks: ð The result of composing two mappings where mapping elements are expressed as triplets < a, type, b > is closed. ð Mapping composition is symmetric in this framework: (<a, type, b > ○ < b, type, c >)-1 =< c, type-1, b > ○ < b, type-1, a> ð The result of composing two mappings does not produce false correspondences between the elements of the two models, i. e. it does not suggest false directed, kinded relationships. ð The Compose operator uses the Unknown relationship to indicate when it is not possible (in general) to suggest a relationship type given only the information expressed in the two mappings. E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 16

Experiment - Setup Ü Experiment goal: ð ð Ü Show that the composition framework is robust when applied to real world application and that we are able to correctly identify problematic cases. We compare it against mappings as morphisms. Five real-world XML schemas in the purchase order domain: CIDR, Excel, Noris, Paragon, and Apertum from www. biztalk. org ð They were used in other projects: Ü [Dragut and Lawrence 2004, Madhavan et al. 2001] And a reference ontology ð to which each XML schema is manually mapped both using morphisms [Dragut and Lawrence 2004] and using the new mapping definition. E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 17

Experiment - Setup Ü Example of XML schemas: ð XML Excel and CIDR schemas E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 18
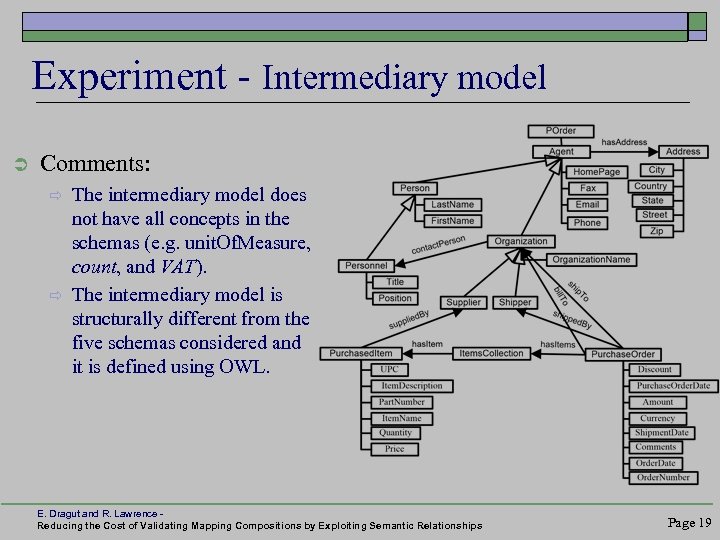
Experiment - Intermediary model Ü Comments: ð ð The intermediary model does not have all concepts in the schemas (e. g. unit. Of. Measure, count, and VAT). The intermediary model is structurally different from the five schemas considered and it is defined using OWL. E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 19

Experiment - Methodology Ü Step 1: map the five schemas to the intermediary model: ð ð Ü Step 2: apply the compose operators to compute direct mappings between the schemas ð ð Ü First, using morphisms Second, using the proposed mapping First, employing composition over morphisms Second, using the new compose operator Step 3: measure the quality of the two compositions in terms of Precision, Recall, and Overall ð A new metric is introduced User Effort. E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 20

Experiment - Stats Ü Ü Overall after composition was computed CIDR, Excel, Noris, Paragon, and Apertum are assigned numbers 1, 2, 3, 4, and 5 respectively. E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 21

Experiment - Stats Ü User effort is the % of mappings that must be validated by a user. ð ð For morphisms, user effort is 100% as there is no way to distinguish true over false relationships. In our framework, it is the ratio of the number of Unknown relationships to the number of all produced relationships. On average it is only 19%. E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 22

End Thank you for your time and patience! E. Dragut and R. Lawrence Reducing the Cost of Validating Mapping Compositions by Exploiting Semantic Relationships Page 23
c0734058aa0fbc5492aea69c314893ae.ppt