Recognizing Safety and Liveness By Bowen Alpern Fred

Recognizing Safety and Liveness By Bowen Alpern, Fred B. Schneider Presented by Choi, Chang-Beom

Content Introduction ◦ ◦ Categorizing Systems Linear-time Temporal Logic Safety & Liveness Model Checking Notation Recognizing Safety Recognizing Liveness Partitioning into Safety and Liveness Conclusion Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST, Chang-Beom Choi 2/39

Introduction What is people’s interest? Consider two objects ◦ S – Specification : What of a system description ◦ I – Implementation : How of a system description ◦ Establish that I conforms with S Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST, Chang-Beom Choi 3/39

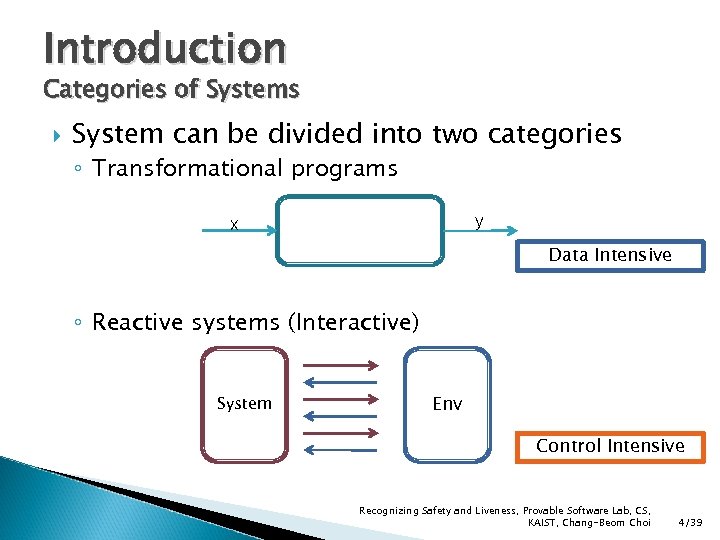
Introduction Categories of Systems System can be divided into two categories ◦ Transformational programs y x Data Intensive ◦ Reactive systems (Interactive) System Env Control Intensive Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST, Chang-Beom Choi 4/39

Introduction Two Type of Transformational program Finite word ◦ Input : finite word ◦ Output : finite word ◦ Model of System : Finite State Automata with finite word Infinite word ◦ Input : infinite word ◦ Output : infinite word ◦ Model of System : Finite State Automata with infinite word Büchi Automata Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST, Chang-Beom Choi 5/39

Introduction How About the Specification of Systems? People wanted to have an accurate way of giving specification Expressiveness • The ability to express all sorts of specifications Linear-time to • Reasonable complexity evaluate Temporalthe specified rules Logic (LTL) • Easy to learn Complexity Pragmatics Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST, Chang-Beom Choi 6/39

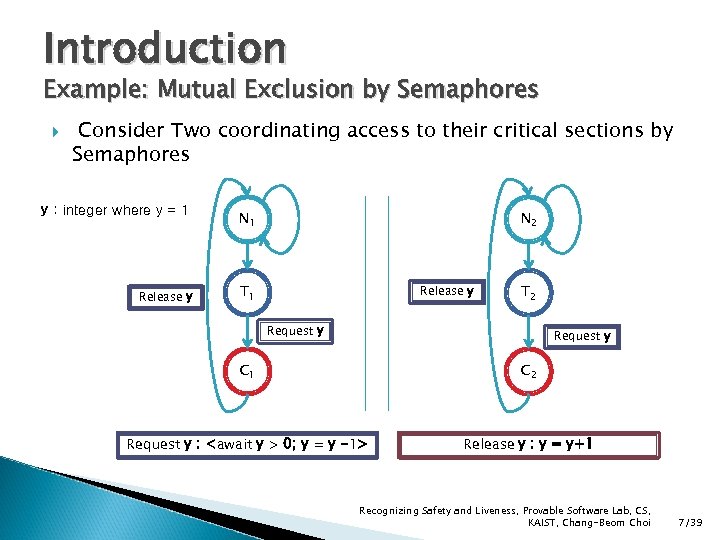
Introduction Example: Mutual Exclusion by Semaphores Consider Two coordinating access to their critical sections by Semaphores y : integer where y = 1 Release y N 1 N 2 T 1 Release y T 2 Request y C 1 C 2 Request y : <await y > 0; y = y -1> Release y : y = y+1 Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST, Chang-Beom Choi 7/39

Introduction Example: Specification of MUTEX by a Property List Safety : bad thing will not happen ◦ The two processes can never visit their respective critical section at the same time □ ┐(C 1 ∧ C 2) Liveness : good thing will happen ◦ Every visit of a process to its trying section is followed by a visit to the critical section of the same process T 1⇒◊ C 1 T 2 ⇒◊ C 2 □ : always ◊ : eventually Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 8/39

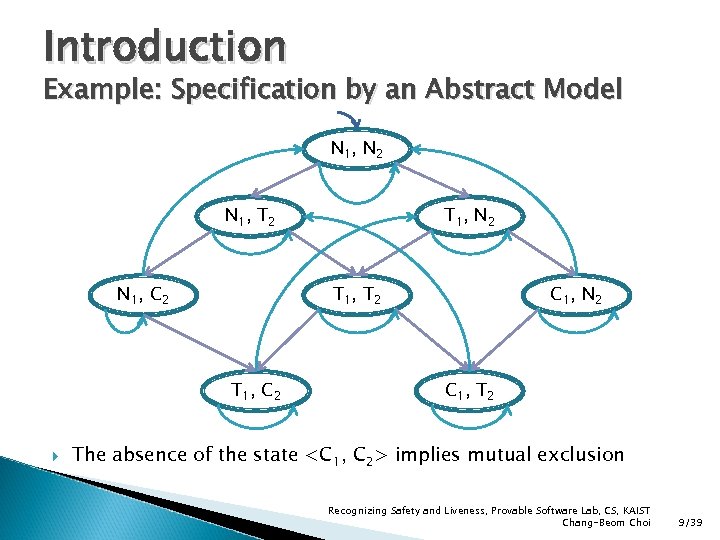
Introduction Example: Specification by an Abstract Model N 1, N 2 N 1, T 2 N 1, C 2 T 1, T 2 T 1, C 2 T 1, N 2 C 1, T 2 The absence of the state <C 1, C 2> implies mutual exclusion Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 9/39

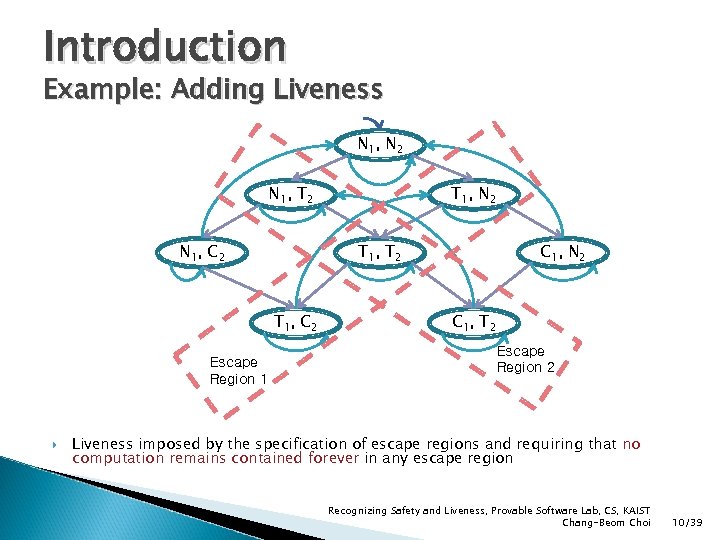
Introduction Example: Adding Liveness N 1, N 2 N 1, T 2 N 1, C 2 T 1, T 2 T 1, C 2 Escape Region 1 T 1, N 2 C 1, T 2 Escape Region 2 Liveness imposed by the specification of escape regions and requiring that no computation remains contained forever in any escape region Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 10/39

Introduction Model Checking For a system T and a specification formula φ we say that : T ⊨ φ if Lω(T) ⊆ models(φ) ◦ models(φ) = {σ ∈ (2 Prop)ω |σ⊨φ} Translate both the system T and the formula φ to a representation that would allow us to verify such a containment Containment of Büchi Automata ◦ Lω(A 1) ⊆ Lω(A 2) ⇔ Lω(A 1) ∩ Lω(Ac 2) =∅ ⇔ Lω(A 1 ∩ Ac 2) = ∅ ◦ Complementation of Nondeterministic Büchi Automata creates automaton of size n. O(n) Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 11/39

Content Introduction ◦ ◦ Categorizing Systems Linear-time Temporal Logic Safety & Liveness Model Checking Notation Recognizing Safety Recognizing Liveness Partitioning into Safety and Liveness Conclusion Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST, Chang-Beom Choi 12/39

Notation History A program π is assumed to be specified in terms of ◦ Its set of atomic actions Aπ ◦ A predicate Initπ that describes its possible initial states History ◦ Execution of π can be viewed as an infinite sequence of program states σ= s 0 s 1 … ◦ s 0 satisfies Initπ and each following state results from executing a single enabled atomic action Aπ from in the preceding state ◦ Terminating execution : repeating the finial state Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 13/39

Notation Property ◦ Set of infinite sequences of program states ◦ σ⊨P (infinite sequence σ is in property P) ◦ A program satisfies a property P if for each of its histories h, h ⊨ P Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 14/39

Notation Büchi Automata m accepts the sequences of program states that are in L(m), the property it specifies. Definition ◦ A = (Σ, S, S 0, ρ, F) Σ: alphabet (set of program states) S : set of automaton states S 0 : set of initial state ρ : a transition function (S xΣx S) F : a set of accepting states ◦ The input of A is infinite w : a 0, a 1, … (∈ Σ ) ◦ A run is a sequence of states r: s 0, s 1, … (∈ Sω) Initiation: s 0 ∈ S 0 ω Consecution : si+1∈ρ(si, ai) Inf(r) : {s: s= si for infinitely many i-s} Acceptance : Inf(r) ∩ F = ∅ Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 15/39

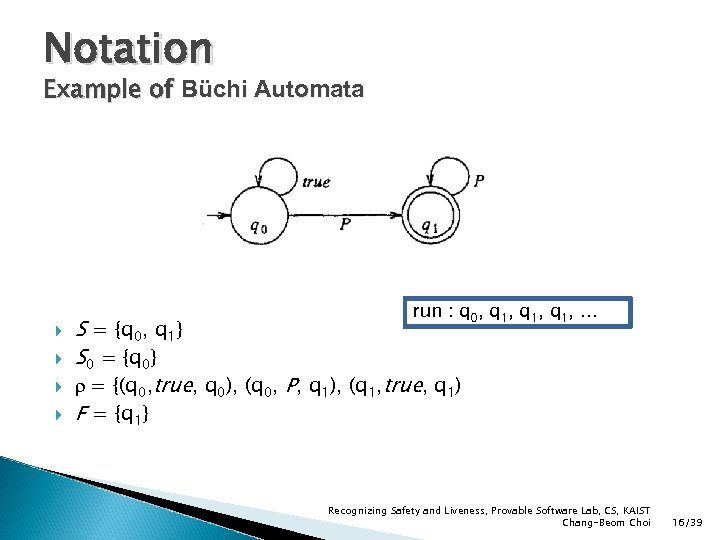
Notation Example of Büchi Automata run : q 0, q 1, … S = {q 0, q 1} S 0 = {q 0} ρ = {(q 0, true, q 0), (q 0, P, q 1), (q 1, true, q 1) F = {q 1} Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 16/39

Notation Reduced Büchi Automata Büchi automaton is reduced if from every state there is a path to an accepting state ◦ Given an arbitrary Büchi automaton, an equivalent reduced Büchi automaton can always be obtained by deleting every state from which no accepting state is reachable ◦ If the next symbol read by Büchi automaton satisfies no transition predicate, the input is rejected; in this case we say the transition is undefined Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 17/39

Notation Additional Definitions σ[i] = si σ[…i] = s 0 s 1…si σ[i…] = sisi+1… |σ| = the length of σ(if ω is σ infinite) Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 18/39

Content Introduction ◦ ◦ Categorizing Systems Linear-time Temporal Logic Safety & Liveness Model Checking Notation Recognizing Safety Recognizing Liveness Partitioning into Safety and Liveness Conclusion Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST, Chang-Beom Choi 19/39

Recognizing Safety Properties Formal Definition Safety property : “bad thing” does not happen What is “bad thing”? ◦ Attempting an undefined transition ◦ If “bad thing” happens in every run while reading an input, the Büchi automaton will not accept that input ◦ If “bad thing” happens in an infinite sequence σ, then it must do so after some finite prefix and must be irremediable. Safety : (∀σ: σ∈ Σω : σ ⊨ P ⇔ (∀ i: 0 ≤i : (∀ β: β ∈ Σω : σ[…i]β⊨ P ))) Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 20/39

Recognizing Safety Properties RBA and Safety Properties Closure cl(m) The closure of m accepts a safety property ◦ For a reduced Büchi automaton m, cl(m) to be the corresponding Büchi automaton in which every stae has been made into an accepting state. ◦ It never rejects an input by failing to enter accepting sates(lack of “good thing”) ◦ It rejects only by attempting an undefined transition Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 21/39

Recognizing Safety Properties Theorem 1 A reduced Büchi automaton m specifies a safety property iff L(m) = L(cl(m)) Proof ◦ ⇒ Assume m specifies safety property L(m) ⊆ L(cl(m)) : trivial L(cl(m)) ⊆ L(m) Let α ∈ L(cl(m)), then α[…i] puts m in state qi Since m is reduced, qi precedes an accepting states β= β 0β 1β 2 … Therefore, α[…i]β causes m to be in accepting states infinitely often, α ∈ L(m) (∀ i: 0 ≤i : (∀ β: β ∈ Σω : α[…i]β ∈ L(m) )) Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 22/39

Recognizing Safety Properties Proving Theorem 1 ⇐ ω σ ∈ L(m) ⇒ (∀ i: 0 ≤i : (∀β: β ∈ Σ : σ[…i]β ∈ L(m) )) Since we can choose β= σ[i+1…] σ ∉L(m) ⇒ ┓(∀ i: 0 ≤i : (∀β: β ∈ Σω : σ[…i]β ∉ L(m) )) Since L(m) =L(cl(m)), σ ∉L(cl(m)) ⇒ ∃ i: 0 ≤i : (∃β: β ∈ Σω : σ[…i]β ∉ L(cl(m) )) σ ∉L(cl(m)) then cl(m) reject σ. Let undefined transition occur upon reading σ[k] ω (∃β: β ∈ Σ : σ[…k]β ∉ L(cl(m) )) Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 23/39

Content Introduction ◦ ◦ Categorizing Systems Linear-time Temporal Logic Safety & Liveness Model Checking Notation Recognizing Safety Recognizing Liveness Partitioning into Safety and Liveness Conclusion Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST, Chang-Beom Choi 24/39

Recognizing Liveness Formal Definition Liveness : “good thing” eventually happens What is “good thing”? ◦ Entering an accepting state infinitely often ◦ Require “good thing” to happen for an input to be accepted ◦ No partial execution is irremediable since if some partial execution were irremediable, then it would be a “bad thing” Liveness (∀α: α∈ Σ*: (∃β: β∈ Σ : αβ ⊨ P)) ω Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 25/39

Recognizing Liveness Theorm 2 A reduced Büchi auomaton m specifies a ω liveness property iff L(cl(m)) =Σ Proof ⇒ Assume m specifies liveness property (∀α: α∈ Σ : (∀ i: 0 ≤i : (∃β: β∈ Σ : α[…i]β ∈ L(m) ))) m does not attempt an undefined transition when reading an input α, cl(m) does accepts α , therefore (∀α: α∈ Σω: α∈ L(cl(m)) ) ω ω Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 26/39

Recognizing Liveness Proving Theorem 2 ⇐ Similar to Proof of Theorem 1 Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 27/39

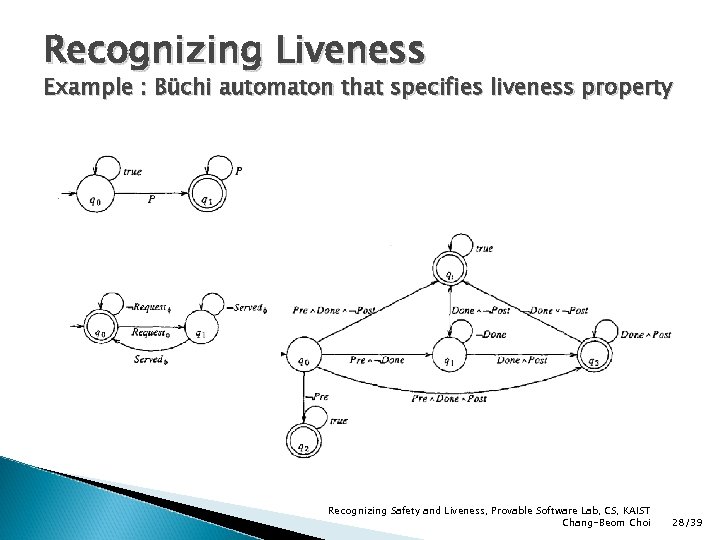
Recognizing Liveness Example : Büchi automaton that specifies liveness property Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 28/39

Content Introduction ◦ ◦ Categorizing Systems Linear-time Temporal Logic Safety & Liveness Model Checking Notation Recognizing Safety Recognizing Liveness Partitioning into Safety and Liveness Conclusion Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST, Chang-Beom Choi 29/39

Partitioning into Safety and Liveness Construct Büchi Automaton Specifying Properties Büchi automaton is equivalent to the conjunction of a safety property and a liveness property Safe(m) ◦ Büchi Automaton which specifies a safety property ◦ It uses cl(m) Live(m) ◦ Büchi Automaton which specifies a liveness property ◦ Construct Büchi automaton s. t. L( Live(m)) = L(m) ∪ (Σω - L(cl(m))) Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 30/39

Partitioning into Safety and Liveness Construct Live(m) Trap state qtrap m is deterministic ◦ A trap state is one that has a transition to itself for all inputs ◦ m augmented by an accepting trap state qtrap ◦ Transition function ρLive every undefined transition of m to put Live(m) in qtrap m is nondeterministic ◦ Use m x env(m) and take accepting states of m or env(m) ω ◦ env(m) = Σ - L(cl(m)) env(m) include a trap state qtrap and the sets of automaton states of m qtrap is the only accepting state of env(m). ◦ Transition function ρenv(qi, s) = qtrap if ρm(qi, s) = ∅, otherwise ρm(qi, s) Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 31/39

Partitioning into Safety and Liveness Lemma L( Live(m)) = L(m) ∪ (Σ - L(cl(m))) ω ◦ m is deterministic Assume α∈ L( Live(m)) Live(m) enters accepting states infinitely ofen when reading α Accepting states are also states of m and α∈ L( m) Otherwise, one of the accepting state is qtrap, therefore α ∉ L(cl(m)) ∴α∈ (Σω - L(cl(m))) (Omission) Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 32/39

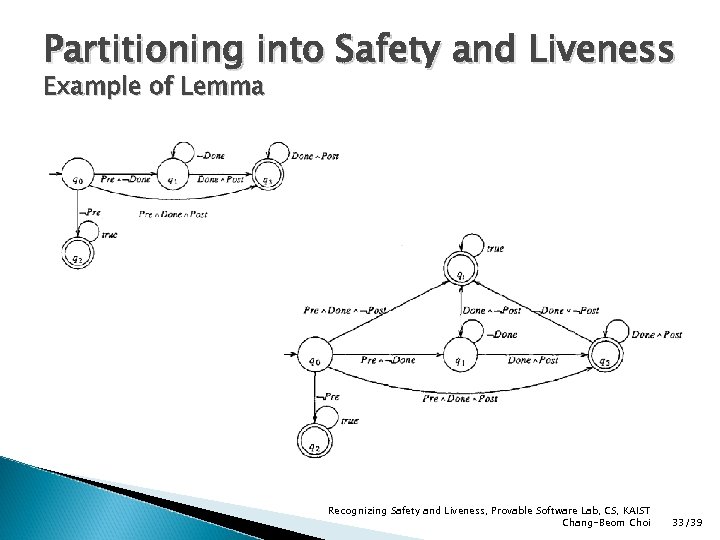
Partitioning into Safety and Liveness Example of Lemma Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 33/39

Partitioning into Safety and Liveness Theorem 3 and Theorem 4 Theorem 3 Safe(m) specifies a safety property Theorem 4 Live(m) specifies a Liveness property ◦ Deterministic case By construction, Live(m) has no undefined transitions. ω Therefore L(cl(Live(m))) = Σ ◦ Nondeterministic case (Omission) Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 34/39

Partitioning into Safety and Liveness Theorem 5 Given a reduced Büchi automaton m, L(m) = L(Safe(m)) ∩ L(Live(m)) Proof ◦ L(Safe(m)) ∩ L(Live(m)) = L(m) ∪ (Σω - L(cl(m))) ∩ L(cl(m)) = (L(m) ∩ L(cl(m)))∪ ((Σω - L(cl(m))) ∩ L(cl(m))) = (L(m) ∩ L(cl(m)))∪ ∅ = L(m) Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 35/39

Content Introduction ◦ ◦ Categorizing Systems Linear-time Temporal Logic Safety & Liveness Model Checking Notation Recognizing Safety Recognizing Liveness Partitioning into Safety and Liveness Conclusion Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST, Chang-Beom Choi 36/39

Conclusion There are lots of things to study DBA vs NBA Generalized Büchi Automata? Simplified Live(m) ? ◦ Expressive power of Deterministic Büchi Automaton is less then Nondeterministic Büchi Automaton Connection between Safety and Liveness properties and Partial and Total Correctness Proving Deterministic Safety and Liveness Properties ◦ Saftey properties specified by deterministic Büchi automata can be proved using only invariance arguments ◦ A variant function of well-foundedness argument is therefore required in proving a liveness property. Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 37/39

Conclusion Next Presentation ? Translate LTL into Automaton ◦ M. Vardi, M. Daniele and F. Giunchiglia, Improved Automata Generation for Linear Temporal Logic, CAV’ 99 Other Topics? Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 38/39

Reference Verification Engineering: A Future Profession. By Amir Pnueli, (A. M. Turing Award Lecture) Sixteenth Annual ACM Symposium on Principles of Distributed Computing (PODC 1990), San Diego, August, 1997 Recognizing Safety and Liveness By Bowen Alpern, Fred B. Schneider, Distributed Computing, vol. 2, num. 3, 1987 Automata-Theoretic Approach to Automated Verification By Amir Pnueli and M. Vardi Lecture Note from http: //www. cs. rice. edu/~vardi/av. html Recognizing Safety and Liveness, Provable Software Lab, CS, KAIST Chang-Beom Choi 39/39