Reciprocal Space Interplanar distances and angles The

Reciprocal Space Interplanar distances and angles

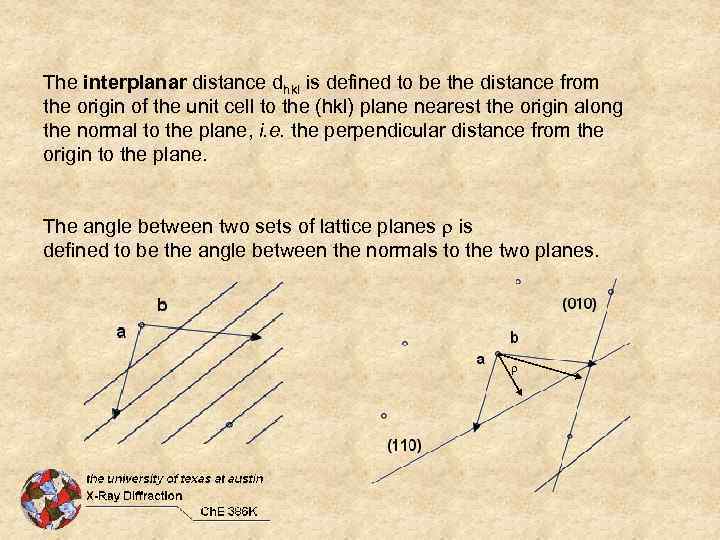The interplanar distance dhkl is defined to be the distance from the origin of the unit cell to the (hkl) plane nearest the origin along the normal to the plane, i. e. the perpendicular distance from the origin to the plane. The angle between two sets of lattice planes is defined to be the angle between the normals to the two planes.

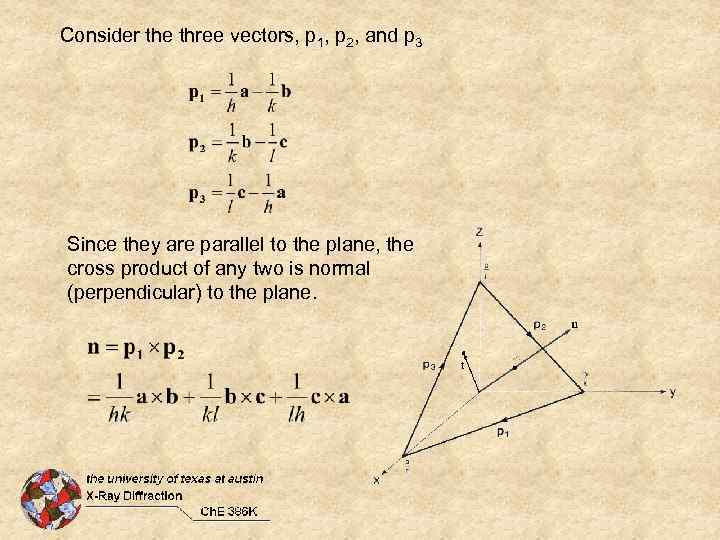Consider the three vectors, p 1, p 2, and p 3 Since they are parallel to the plane, the cross product of any two is normal (perpendicular) to the plane.

If we find the unit normal, n/|n|, and take its dot product with any vector, t, that terminates on the plane, we get the interplanar distance, dhkl. We can also take the dot products of a pair of these normals to determine the angle between the normals. Computationally this is not that easy, unless the crystal axes are all orthogonal, so we take a different approach.

Orthorhombic System All angles are 90°, so the cross products are easily calculated. and

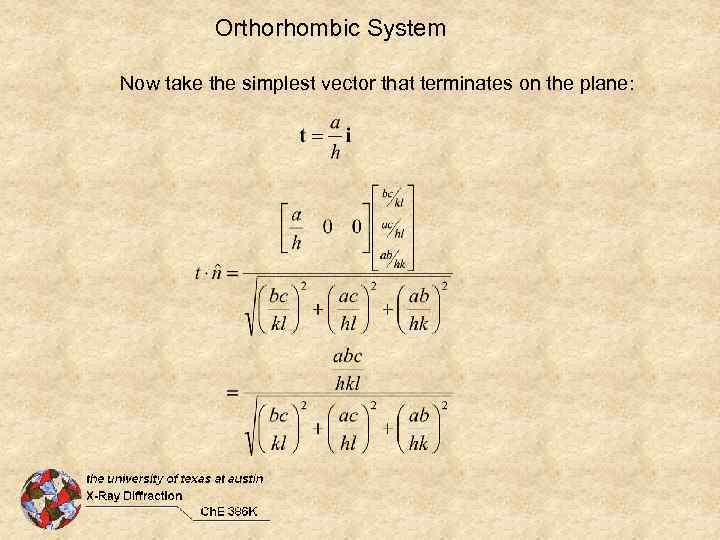Orthorhombic System Now take the simplest vector that terminates on the plane:

Orthorhombic System Simplifying and squaring

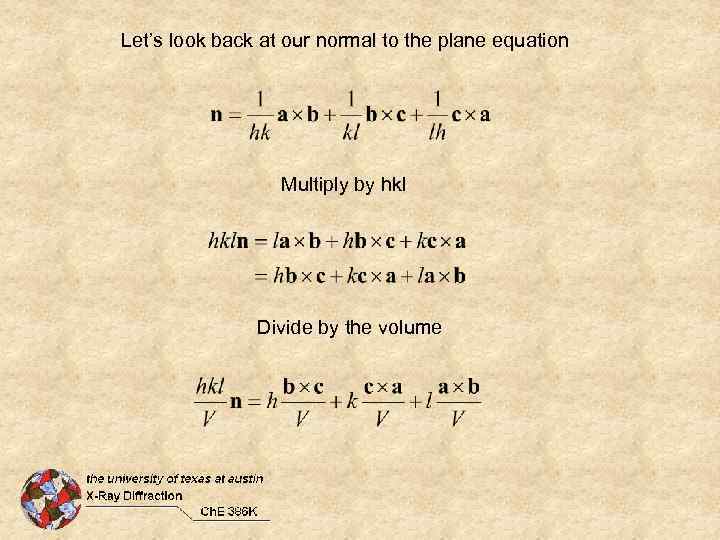Let’s look back at our normal to the plane equation Multiply by hkl Divide by the volume

Consider just the last term of this equation with l = 1. axb is a vector perpendicular to the a-b face with length equal to the surface area contained in the a-b face. So…

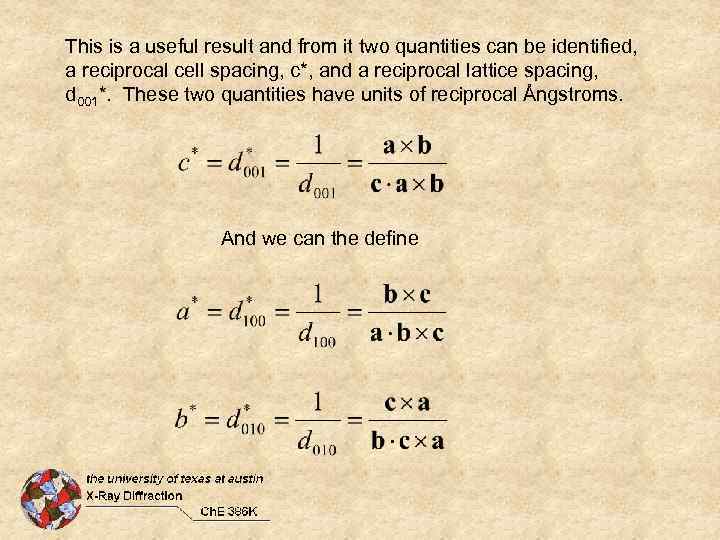This is a useful result and from it two quantities can be identified, a reciprocal cell spacing, c*, and a reciprocal lattice spacing, d 001*. These two quantities have units of reciprocal Ångstroms. And we can the define

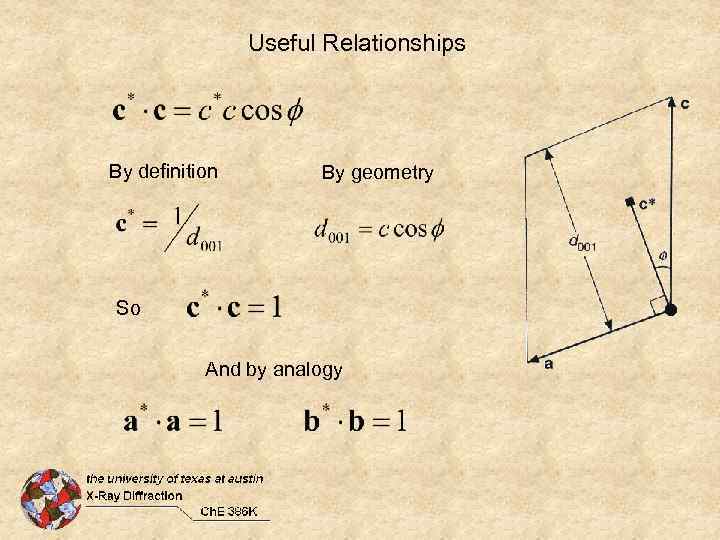Useful Relationships By definition By geometry So And by analogy

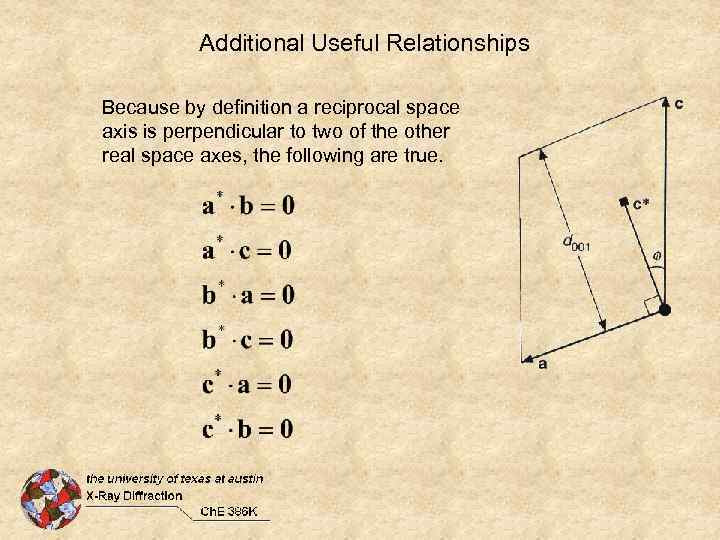Additional Useful Relationships Because by definition a reciprocal space axis is perpendicular to two of the other real space axes, the following are true.

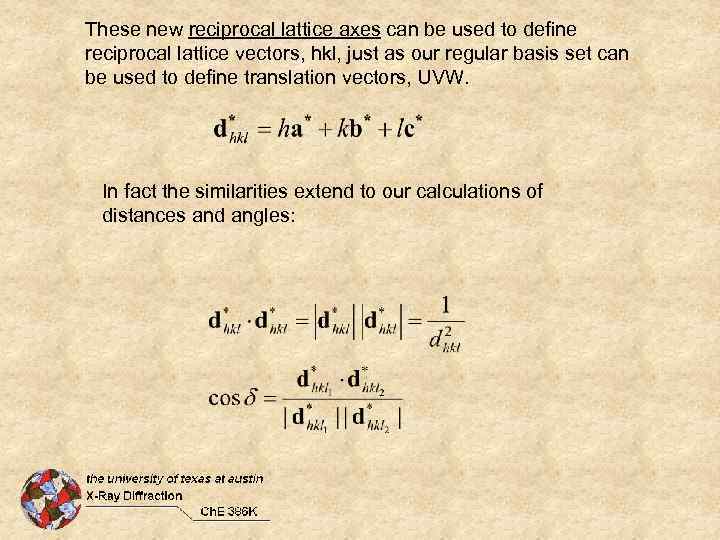These new reciprocal lattice axes can be used to define reciprocal lattice vectors, hkl, just as our regular basis set can be used to define translation vectors, UVW. In fact the similarities extend to our calculations of distances and angles:

Construction of Reciprocal Lattice 1. Identify the basic planes in the direct space lattice, i. e. (001), (010), and (001). 2. Draw normals to these planes from the origin. 3. Mark distances from the origin along these normals proportional to the inverse of the distance from the origin to the direct space planes

Above a monoclinic direct space lattice is transformed (the baxis is perpendicular to the page). Note that the reciprocal lattice in the last panel is also monoclinic with * equal to 180°−. The symmetry system of the reciprocal lattice is the same as the direct lattice.

Reciprocal Metric Tensor The reciprocal metric tensor exists and is defined in an analogous manner to the direct space metric tensor. The good news is that G* can be recovered from G:

Using the reciprocal metric tensor makes calculation of dspaces remarkably easy. Compare to

And also interplanar angles:

Calcite Example Trigonal a = 4. 990Å, c = 17. 061Å

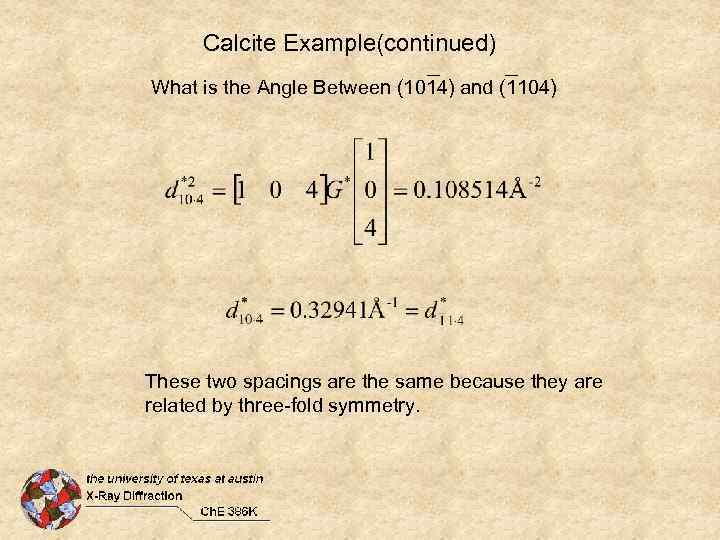Calcite Example(continued) What is the Angle Between (1014) and (1104) These two spacings are the same because they are related by three-fold symmetry.

Calcite Example(continued) So

The following show common direct space – reciprocal space relationships and equations to calculate d-spaces. These are normally found in symmetry/crystallography texts and are listed by crystal system. However, remembering a couple of simple facts about the metric tensor and it’s inverse leads to the same results.

Direct Space to Reciprocal Space

Reciprocal Space to Direct Space

Dspace Equations