Reciprocal Space Interplanar distances and angles The interplanar















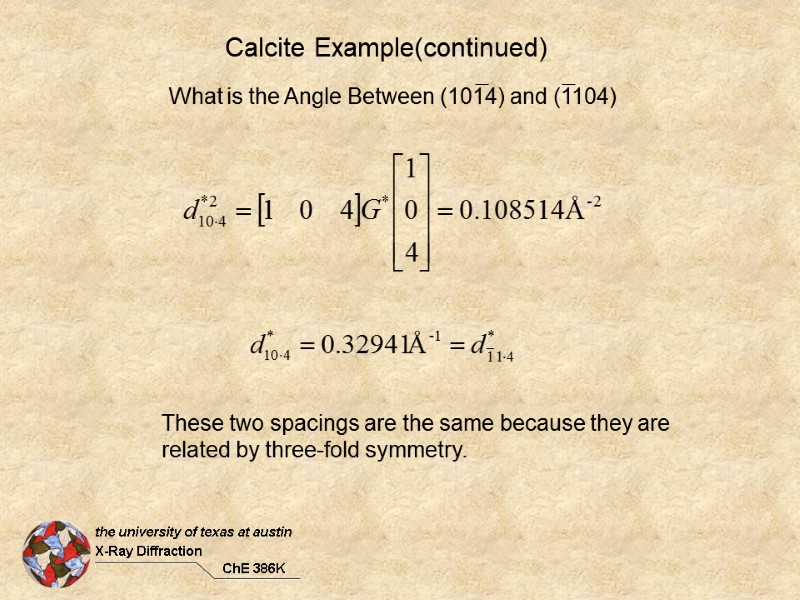





6590-23_reciprocal_space.ppt
- Количество слайдов: 25
 Reciprocal Space Interplanar distances and angles
Reciprocal Space Interplanar distances and angles
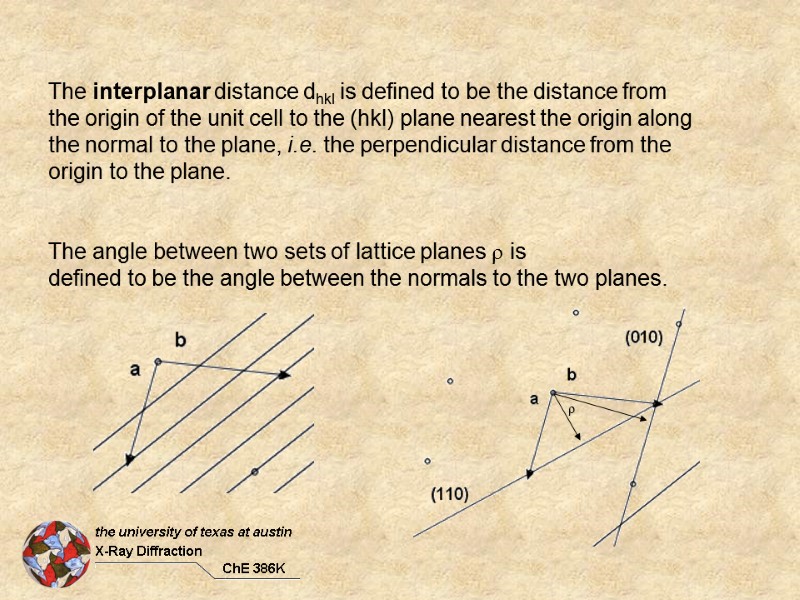
 The interplanar distance dhkl is defined to be the distance from the origin of the unit cell to the (hkl) plane nearest the origin along the normal to the plane, i.e. the perpendicular distance from the origin to the plane. The angle between two sets of lattice planes is defined to be the angle between the normals to the two planes.
The interplanar distance dhkl is defined to be the distance from the origin of the unit cell to the (hkl) plane nearest the origin along the normal to the plane, i.e. the perpendicular distance from the origin to the plane. The angle between two sets of lattice planes is defined to be the angle between the normals to the two planes.
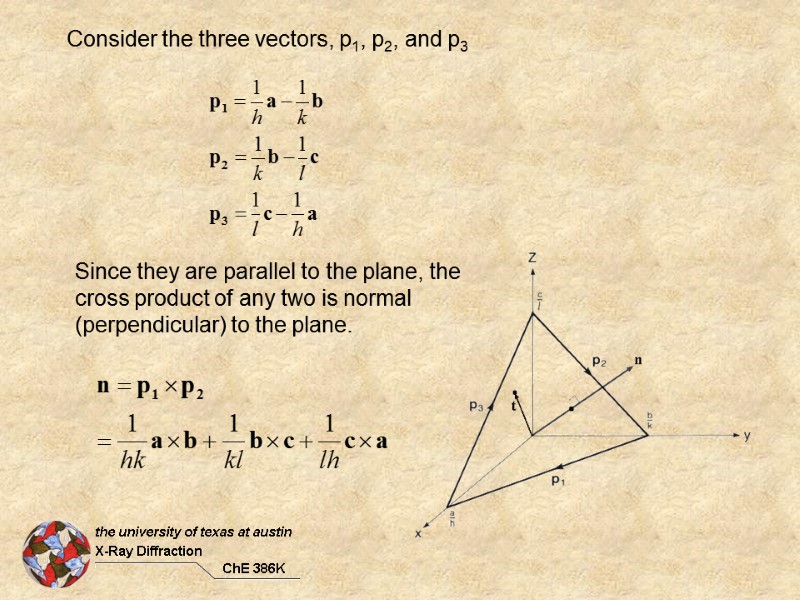
 Consider the three vectors, p1, p2, and p3 Since they are parallel to the plane, the cross product of any two is normal (perpendicular) to the plane.
Consider the three vectors, p1, p2, and p3 Since they are parallel to the plane, the cross product of any two is normal (perpendicular) to the plane.
 If we find the unit normal, n/|n|, and take its dot product with any vector, t, that terminates on the plane, we get the interplanar distance, dhkl. We can also take the dot products of a pair of these normals to determine the angle between the normals. Computationally this is not that easy, unless the crystal axes are all orthogonal, so we take a different approach.
If we find the unit normal, n/|n|, and take its dot product with any vector, t, that terminates on the plane, we get the interplanar distance, dhkl. We can also take the dot products of a pair of these normals to determine the angle between the normals. Computationally this is not that easy, unless the crystal axes are all orthogonal, so we take a different approach.
 Orthorhombic System All angles are 90°, so the cross products are easily calculated. and
Orthorhombic System All angles are 90°, so the cross products are easily calculated. and
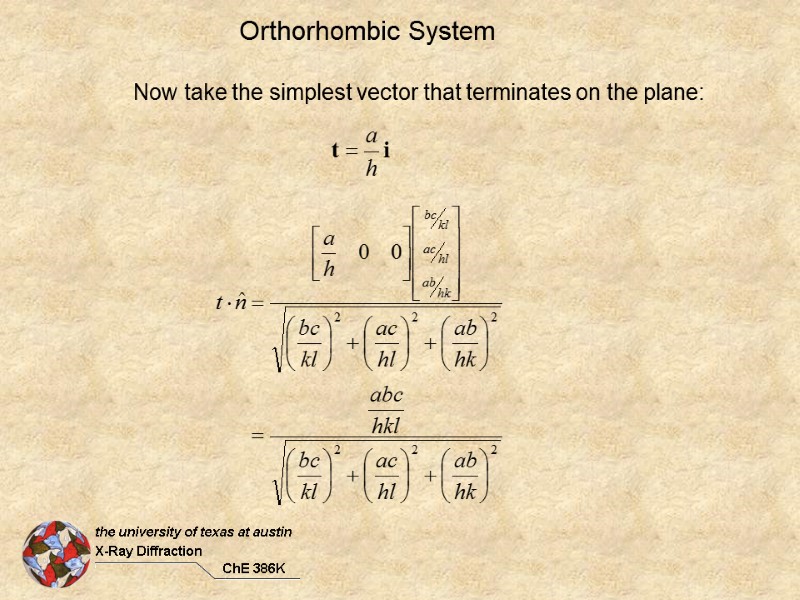
 Orthorhombic System Now take the simplest vector that terminates on the plane:
Orthorhombic System Now take the simplest vector that terminates on the plane:
 Orthorhombic System Simplifying and squaring
Orthorhombic System Simplifying and squaring
 Let’s look back at our normal to the plane equation Multiply by hkl Divide by the volume
Let’s look back at our normal to the plane equation Multiply by hkl Divide by the volume
 Consider just the last term of this equation with l = 1. axb is a vector perpendicular to the a-b face with length equal to the surface area contained in the a-b face. So…
Consider just the last term of this equation with l = 1. axb is a vector perpendicular to the a-b face with length equal to the surface area contained in the a-b face. So…
 This is a useful result and from it two quantities can be identified, a reciprocal cell spacing, c*, and a reciprocal lattice spacing, d001*. These two quantities have units of reciprocal Ångstroms. And we can the define
This is a useful result and from it two quantities can be identified, a reciprocal cell spacing, c*, and a reciprocal lattice spacing, d001*. These two quantities have units of reciprocal Ångstroms. And we can the define
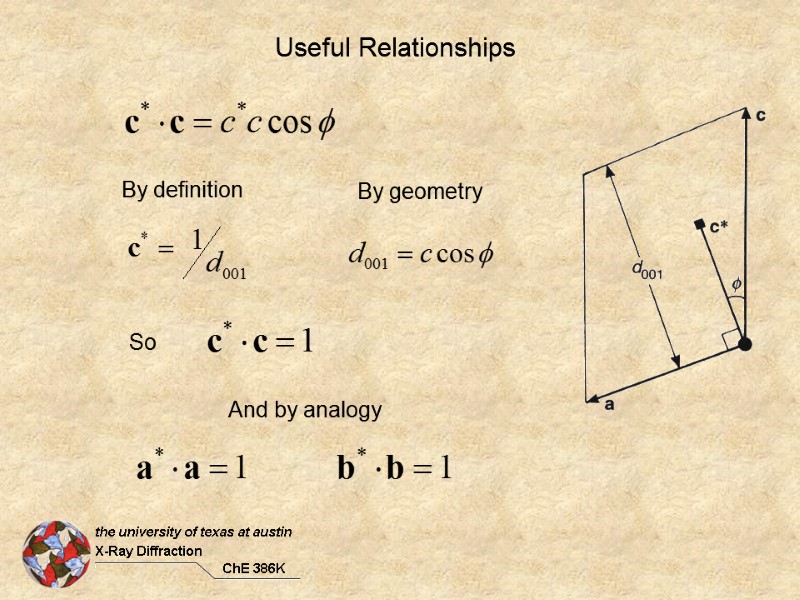
 Useful Relationships By definition By geometry So And by analogy
Useful Relationships By definition By geometry So And by analogy
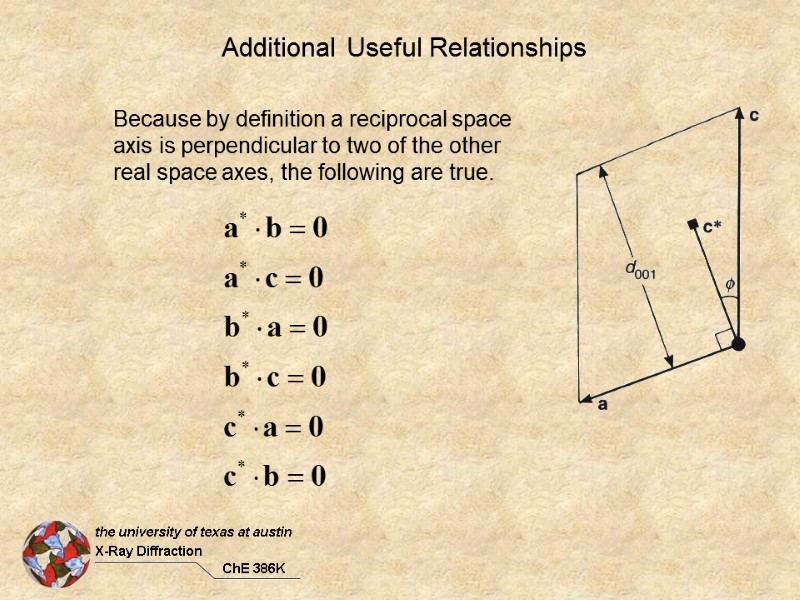
 Additional Useful Relationships Because by definition a reciprocal space axis is perpendicular to two of the other real space axes, the following are true.
Additional Useful Relationships Because by definition a reciprocal space axis is perpendicular to two of the other real space axes, the following are true.
 These new reciprocal lattice axes can be used to define reciprocal lattice vectors, hkl, just as our regular basis set can be used to define translation vectors, UVW. In fact the similarities extend to our calculations of distances and angles:
These new reciprocal lattice axes can be used to define reciprocal lattice vectors, hkl, just as our regular basis set can be used to define translation vectors, UVW. In fact the similarities extend to our calculations of distances and angles:
 Construction of Reciprocal Lattice Identify the basic planes in the direct space lattice, i.e. (001), (010), and (001). Draw normals to these planes from the origin. Mark distances from the origin along these normals proportional to the inverse of the distance from the origin to the direct space planes
Construction of Reciprocal Lattice Identify the basic planes in the direct space lattice, i.e. (001), (010), and (001). Draw normals to these planes from the origin. Mark distances from the origin along these normals proportional to the inverse of the distance from the origin to the direct space planes
 Above a monoclinic direct space lattice is transformed (the b-axis is perpendicular to the page). Note that the reciprocal lattice in the last panel is also monoclinic with * equal to 180°−. The symmetry system of the reciprocal lattice is the same as the direct lattice.
Above a monoclinic direct space lattice is transformed (the b-axis is perpendicular to the page). Note that the reciprocal lattice in the last panel is also monoclinic with * equal to 180°−. The symmetry system of the reciprocal lattice is the same as the direct lattice.
 Reciprocal Metric Tensor The reciprocal metric tensor exists and is defined in an analogous manner to the direct space metric tensor. The good news is that G* can be recovered from G:
Reciprocal Metric Tensor The reciprocal metric tensor exists and is defined in an analogous manner to the direct space metric tensor. The good news is that G* can be recovered from G:
 Using the reciprocal metric tensor makes calculation of d-spaces remarkably easy. Compare to
Using the reciprocal metric tensor makes calculation of d-spaces remarkably easy. Compare to
 And also interplanar angles:
And also interplanar angles:
 Calcite Example Trigonal a = 4.990Å, c = 17.061Å
Calcite Example Trigonal a = 4.990Å, c = 17.061Å
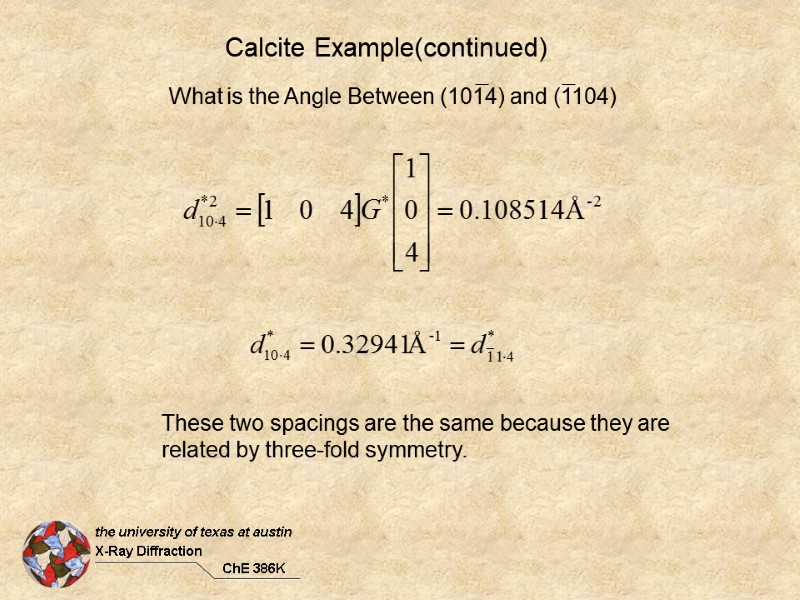 These two spacings are the same because they are related by three-fold symmetry. Calcite Example(continued)
These two spacings are the same because they are related by three-fold symmetry. Calcite Example(continued)
 Calcite Example(continued) So
Calcite Example(continued) So
 The following show common direct space – reciprocal space relationships and equations to calculate d-spaces. These are normally found in symmetry/crystallography texts and are listed by crystal system. However, remembering a couple of simple facts about the metric tensor and it’s inverse leads to the same results.
The following show common direct space – reciprocal space relationships and equations to calculate d-spaces. These are normally found in symmetry/crystallography texts and are listed by crystal system. However, remembering a couple of simple facts about the metric tensor and it’s inverse leads to the same results.
 Direct Space to Reciprocal Space
Direct Space to Reciprocal Space
 Reciprocal Space to Direct Space
Reciprocal Space to Direct Space
 Dspace Equations
Dspace Equations

