Recent Methods and Problems in Authentication Protocol Analysis

Recent Methods and Problems in Authentication Protocol Analysis Jonathan Millen SRI International Menlo Park, CA, USA millen@csl. sri. com WADIS '03 December 6, 2003

Outline l Background – What is cryptographic protocol analysis – Why is it a hard problem – Overview of analysis approaches l Recent Work – – Strand spaces Digression - group management protocol analysis The constraint solver Continuing research problems

Resources l CAPSL Web Site – www. csl. sri. com/users/millen/capsl l Bibliography – capsl/protsec. bib (references like [AB 99]) l Clark-Jacob Library – www. cs. york. ac. uk/security/Publications. html – capsl/library. html l SPORE Library (Comon) – www. lsv. ens-cachan. fr/spore l Constraint solver tutorial and Prolog code – capsl/constraints. html l Ryan-Schneider text, Crypto. Protocol Analysis: CSP

Cryptosystems l Cryptosystem: algorithm for encrypting plaintext into ciphertext, and decrypting, using keys. l Cryptographic protocol: exchange of messages for distributing keys or applying a cryptosystem to data. l Symmetric-key cryptosystem: the same key is used for encrypting and decrypting. – Examples: DES, IDEA, Skipjack, Blowfish, RC 4, AES (Rijndael) l Public-key cryptosystem: different keys are used for encrypting and decrypting. The encryption key may be made public. – Examples: RSA, El Gamal, Elliptic curve – Diffie-Hellman (key agreement)

Cryptographic Protocols l For key distribution: provide two parties with keys suitable for private or authenticated communication l For authentication: to provide one party with assurance that a message was sent by another party in the same session. l For other purposes: fair exchange, auctions, voting, … l Examples – – – SSL - in browsers (now TLS) Kerberos - remote unitary login EKE, SRP - password based Cybercash - electronic commerce IKE, ISAKMP, JFK – by IETF l New ones are continually proposed

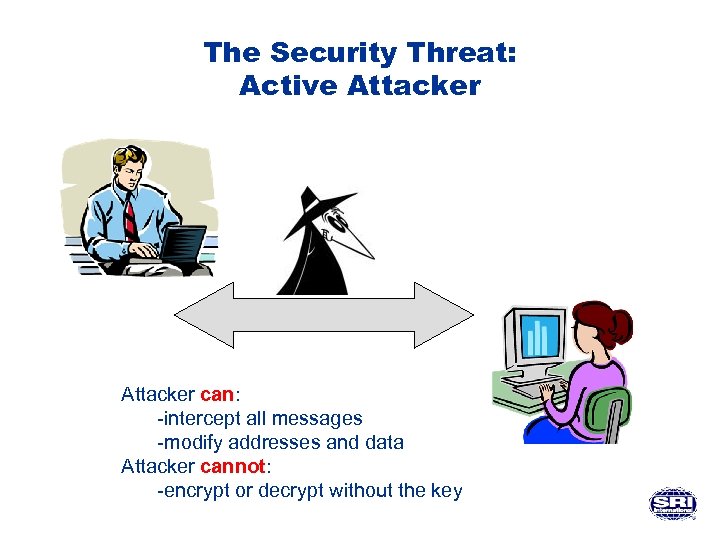
The Security Threat: Active Attacker can: -intercept all messages -modify addresses and data Attacker cannot: -encrypt or decrypt without the key

Protocol Vulnerabilities Ground Rules l "Attacker" synonyms: – intruder, spy, saboteur, penetrator, enemy, adversary l Attacker can intercept any message – Ability to read, record, misdeliver any message – Method: sniffers, and intrusions in firewalls or routers l Attacker can introduce new messages – Construct messages using primitive operations – Falsify (unencrypted) source, destination addresses l Strong encryption assumption: an attacker cannot decrypt any message without the key. l Attacker is a legitimate network user with a name, key, etc. l Other users follow the protocol l This is often called the “Dolev-Yao” model [DY 83]

Example - Needham-Schroeder l The Needham-Schroeder symmetric-key protocol [NS 78] A S: A, B, Na S A: {Na, B, Kc, {Kc, A}K(B) }K(A) A B: {Kc, A}K(B) B A: {Nb}Kc A B: {Nb-1}Kc l l l A, B are “principals; ” S is a trusted key server K(A) is a secret key shared by A and S {X, Y}K means: X concatenated with Y, encrypted with K Na, Nb are “nonces; ” fresh (not used before) Kc is a fresh connection key Denning-Sacco replay attack in 1981 [DS 81]

Denning-Sacco Attack l Assume that the attacker has recorded a previous session, and compromised the connection key Kc used in that session. … first part omitted A B: {Kc, A}K(B) attacker replay of old message B A: {Nb}Kc A B: {Nb-1}Kc forged by attacker l B now believes he shares a fresh secret key Kc with A. l Denning-Sacco moral: use a timestamp (calendar clock value) to detect replay of old messages. – Better use of nonces could also work

Folklore - Attack Terms l Replay: record and later re-introduce a message or part l Masquerading: pretending to be another party – Forge source address l Man-in-the-middle: pass messages through to another session A X B l Oracle: take advantage of normal protocol responses as encryption and decryption “services” l Type confusion: substitution of a different type of message field (e. g. , key vs. nonce) l Parallel attack: takes advantage of two or more concurrent protocol runs of the same role, different sessions

Design Principles l Abadi-Needham “prudent engineering practice” paraphrased – See [AN 94]; also Anderson and Needham [AN 95] 1. Every message should say what it means. 2. The conditions for a message to be acted on should be clearly set out. 3. Mention the principal’s name explicitly in the message if it is essential to the meaning. 4. Be clear as to why encryption is being done. 5. Don’t assume a principal knows the content of encrypted material that is signed by that principal. 6. Be clear on what properties you are assuming about nonces. 7. Predictable quantities used for challenge-response should be protected from replay.

More Design Principles 8. Timestamps must take into account local clock variation and clock maintenance mechanisms. 9. A key may have been used recently, yet be old. 10. If an encoding is used to present the meaning of a message, then it should be possible to tell which encoding is being used. 11. The protocol designer should know which trust relations his protocol depends on. l Good advice, but… – Are you sure when you have followed all of them? – Is the protocol guaranteed to be secure then? – Is it optimal and/or minimal?

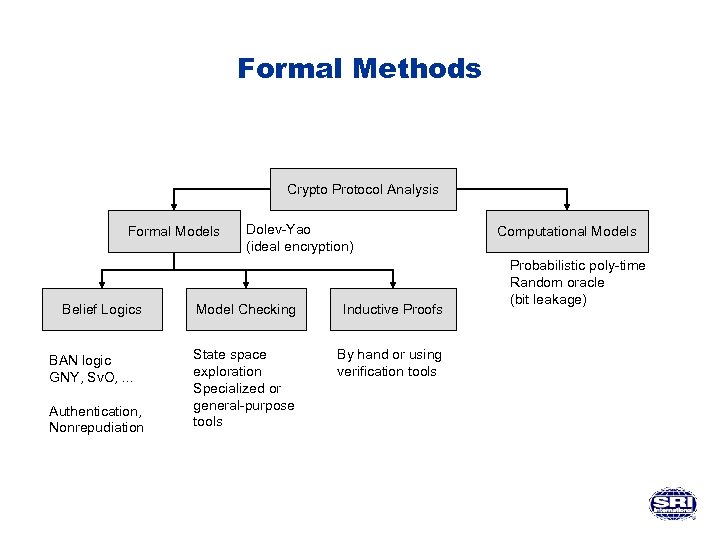
Formal Methods Crypto Protocol Analysis Formal Models Belief Logics BAN logic GNY, Sv. O, . . . Authentication, Nonrepudiation Dolev-Yao (ideal encryption) Model Checking Inductive Proofs State space exploration Specialized or general-purpose tools By hand or using verification tools Computational Models Probabilistic poly-time Random oracle (bit leakage)

Why Protocol Analysis is Hard

Protocol Analysis is Undecidable l Several proofs – First undecidability proof by Even & Goldreich, [EG 83] – Simpler use of Post Correspondence problem by Heintze & Tygar, [HT 96] l Undecidability comes from unboundedness in the model – Number of protocol instances (runs, sessions) is unbounded – Messages from attacker are unbounded in structural depth – Number of possible values for some data fields is infinite

BAN Logic l Papers – Burrows, Abadi, Needham, “A logic of authentication, ” ACM Trans. Computer Systems 8(1), 1990 (also DEC SRC Research Rpt 39) – Subsequent extensions, e. g. , GNY logic Gong, Needham, Yahalom, “Reasoning about belief in cryptographic protocols, ” 1990 IEEE Symposium on Security and Privacy l Approach – Modal logic of belief plus specialized predicates and inference rules Example: B believes A said (K is fresh) Example: if A shares K with B and B sees {X}K then A said X – – Protocol messages are “idealized” into logical statements Objective is to prove that both parties share common beliefs Logic of “authentication” Elegant, popular

The Problem with BAN l Nessett noted problem [Nes 90] – A B: {T, K}KA-1 – Shared key K given away by encryption with private key of pair – A can still believe A shares K with B l Secrecy failures may be subtle – Secrecy analysis must be prior to authentication proof – Prove that good keys or shared secrets are not compromised during the protocol (due to an attack) l Logics like this address authentication, must use other techniques to verify confidentiality where assumed/needed

Early Specialized Model Checkers l Interrogator [MCF 87, Mil 95] – Prolog program – Backward state search for attack from goal state pattern – No guarantee of completeness or termination l NRL Protocol Analyzer [Mea 91, Mea 96 a] – – – Prolog program Backward state search, plus Generation of "unreachable" languages No guarantee of completeness or termination Can sometimes prove a protocol correct

General-Purpose Model Checker Applications l Application of software tools designed for hardware CAD Verification by state space exploration - exhaustive on model l Like earlier Prolog tool approach, but Special algorithms (BDD, SAT, etc. ) Require finite model bounds on number of sessions, message structure, etc. Fully automatic once protocol is encoded l Researchers: Roscoe [Ros 95], using FDR (the first) Mitchell, et al, using Murphi [MMS 97] Marrero, et al, using SMV [MCJ 97] Denker, et al, using Maude [DMT 98] … and more

Model-Checking Observations l Very effective at finding flaws, but l No guarantee of correctness, due to artificial finite bounds – Bound on message structure depth later found unnecessary l Setup and analysis is quick when done by experts – Automatic translation from simple message-list format to modelchecker input is possible [Lowe's Casper: Low 98 a] l Successful example: Lowe attack on Needham-Schroeder public -key protocol, using FDR [Low 96]

Lowe Small-System Result l Theorem: if Assumptions 1 -6 (below) are satisfied, then any secrecy breach can be demonstrated in a “small system” with only one instance of each role. [Low 98 b] 1. 2. 3. 4. 5. 6. Functions that return keys are one-to-one (no key coincidence) All short-term secrets are fresh No long-term keys are (normally) sent (as data) in messages Encrypted message components mention all roles Encrypted message components are textually distinct No temporary secrets (secrets must not be revealed after use) l Example: (Davis-Swick) A B: {B, T}sk(A, B) B A: {T, A}sk(B, A) – This satisfies the assumptions if sk(A, B) sk(B, A) (for 1) T is a recognizably different type from principal (for 5)

Recent Specialized Methods l Athena – – – Song/Berezin/Perrig [SBP 01] ML program Uses strand-space model (free algebra, atomic keys) Special-purpose model checker Very fast Usually terminates, no fixed bound l Bounded-Process Decidable – – Bounded set of legitimate processes Decidable despite no bound on message term complexity Shown NP-complete by Rusinowitch/Turuani [RT 01] Constraint solver is in this category

Inductive Proofs l Approach: like proofs of program correctness – Induction to prove “loop invariant” l State-transition model, objective is security invariant l General-purpose specification/verification system support – – Kemmerer, using Ina Jo and ITP [Kem 89] (the first) Paulson, using Isabelle [Paul 98] (the new wave) Dutertre and Schneider, using PVS [DS 97] Bolignano, using Coq [Bol 97] l Can also be done manually – Schneider, using CSP [Sch 98] – Thayer et al, using Strand Spaces [THG 98] – Spi calculus proofs (Abadi, Gordon, . . . ) l Full guarantee of correctness (with respect to model) – No bounds imposed – Proofs include secrecy – But they are usually hard work

Strand Spaces Thayer, Herzog, Guttman [THG 98] Message: ground term in free algebra over symbolic constants, with pairs and encryption Message does not include "A B" header Strand: sequence of nodes Node is labeled with +/- message Bundle: causal partial ordering of nodes in strands Example: NSPK “A” strand +{n, a}kb -{n, r}ka +{r}kb “B” strand -{n, a}kb Penetrator strands, for primitive operations Examples: x {x}k +{n, r}ka k-1 y x {x, y} Penetrator strands are universal

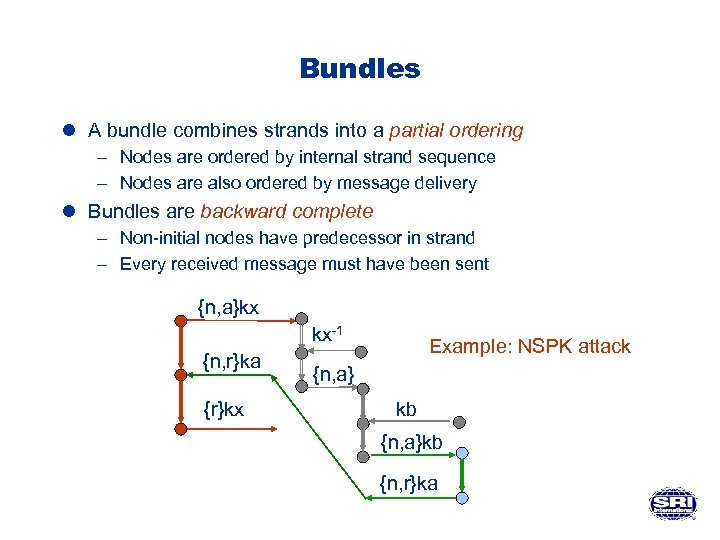
Bundles l A bundle combines strands into a partial ordering – Nodes are ordered by internal strand sequence – Nodes are also ordered by message delivery l Bundles are backward complete – Non-initial nodes have predecessor in strand – Every received message must have been sent {n, a}kx kx-1 {n, r}ka {r}kx Example: NSPK attack {n, a} kb {n, a}kb {n, r}ka

Parametric Strand Specification Suggested by [Son 99] and [CDLMS 00] A-role strand "A"(A, B, Na, Nb) Protocol A B: {A, Na}pk(B) B A: {Nb, Na}pk(A) A B: {Nb}pk(B) +{A, Na}pk(B) -{Nb, Na}pk(A) Na is a nonce generated by "A" roles A, B, Na, Nb (initial capitals) are variables +{Nb}pk(B) Addresses lost There's also a B-role strand Semibundle: incomplete bundle, partially instantiated strands

Example Spec l Yahalom protocol "A"(A, B, S, Na, Nb, K) = + {A, Na} – {{B, K, Na, Nb}sk(A), {Nb}K} "B"(A, B, S, Na, Nb, K, T) = – {A, Na} + {B, {A, Na, Nb}sk(B)} – {T, {A, K}sk(B)} + {T, {Nb}K} A B: A, Na B S: B, {A, Na, Nb}sk(B) S B: {B, K, Na, Nb}sk(A), {A, K}sk(B) B A: {B, K, Na, Nb}sk(A), {Nb}K Term T encrypted for A is just passed on "S"(A, B, S, Na, Nb, K) = – {B, {A, Na, Nb}sk(B)} + {{B, K, Na, Nb}sk(A), {A, K}sk(B)}

Characteristics of Spec Style l Keys may be constructed – Symmetric key may be any term, not just constants – Public keys constructed with pk(A) – Secret keys sk(A) assumed to be shared with server l Free term algebra (no term reductions or relations) – Advantage: WYSIWYG simplicity – Can't specify decryption explicitly in protocol spec – Some loss of generality (EV-freedom discussion) l Untyped – Advantage or disadvantage? – Typing can be simulated with type-coercion functions l Don’t yet handle commutative operations (xor, exponentiation)

Free Term Algebra Question Suppose that a protocol is expressible (in parametric strand style) using a free term algebra to represent encryption. (Write e(X, K) for {X}K so we can introduce d(X, K) below) Example strand: S(A, B, X, K) = -e({X, A}, K) +e({X, B}, K) Assume that the attacker can perform decryption transformations as usual, such as: e(X, K), K X Can new attacks be discovered by adding an explicit decryption operator with cancellation relations? d(e(X, K) X e(d(X, K) X

Counterexample “A” strand “B” strand +e(s, k) -e(e(X, c), k) +X Assumptions: s is a secret constant k is a secret key c is a compromised key X is a variable Observation: if e(s, k) is acceptable as e(e(X, c), k) then s = e(X, c) and X = d(s, c) so the attacker can get s. A free term algebra can't see this.

Remarks What's missing: ability to decrypt something that was not encrypted Generality is restored if e(X, K) is disallowed for any variable X Spec is "EV-free" if this restriction is satisfied (OK to have X in context, e. g. , e({X, a}, K)) "On the freedom of decryption, " Millen, IPL 86(2003) All this applies to public key encryption too (Lynch) Why use free term algebra model? Analysis advantages: efficient constraint solving, proof of completeness and termination EV-freedom is realistic But free algebras still can't handle group management protocols. . .

Multicast Group Management l Multicast group members share a group key l A suite of protocols is used to perform different tasks – – – Addition of a new member to the group (rekey) Deletion of a member from the group (rekey) Merge two groups or split one into two Distribute new group key Application-dependent tasks l Different methods for key distribution – Group Diffie-Hellman, key hierarchy, … l Secrecy objectives – Backward access control: new members can't read old messages – Forward access control: deleted members can't read new messages

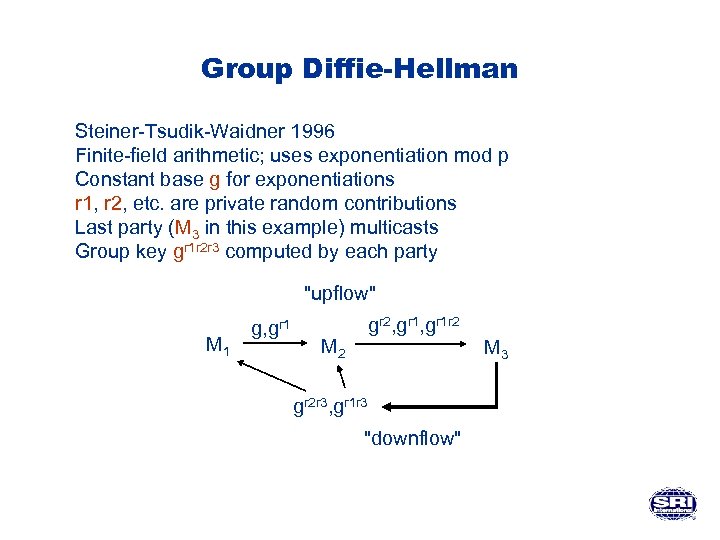
Group Diffie-Hellman Steiner-Tsudik-Waidner 1996 Finite-field arithmetic; uses exponentiation mod p Constant base g for exponentiations r 1, r 2, etc. are private random contributions Last party (M 3 in this example) multicasts Group key gr 1 r 2 r 3 computed by each party "upflow" M 1 g, gr 1 gr 2, gr 1 r 2 M 2 gr 2 r 3, gr 1 r 3 "downflow" M 3

Need for Authentication l Attacker can misdeliver upflow M 1 message as downflow g, gr 1 l Party computes wrong group key, something public Attacker r 1 g, g l This is a problem for two-party Diffie Hellman also l First attempt at solution: AGDH M 1 computes group (Authenticated) key as gr 1 – Assume pairwise shared keys – Include key with downflow terms gr 2 r 3 k 13, gr 1 r 3 k 23 – Insufficient: Pereira-Quisquater attack [PQ 01]

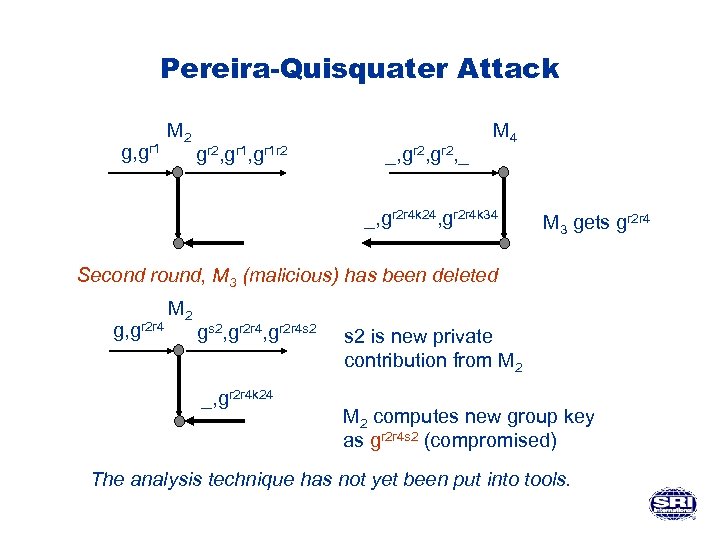
Pereira-Quisquater Attack g, gr 1 M 2 gr 2, gr 1 r 2 _, gr 2, _ M 4 _, gr 2 r 4 k 24, gr 2 r 4 k 34 M 3 gets gr 2 r 4 Second round, M 3 (malicious) has been deleted g, gr 2 r 4 M 2 gs 2, gr 2 r 4 s 2 _, gr 2 r 4 k 24 s 2 is new private contribution from M 2 computes new group key as gr 2 r 4 s 2 (compromised) The analysis technique has not yet been put into tools.

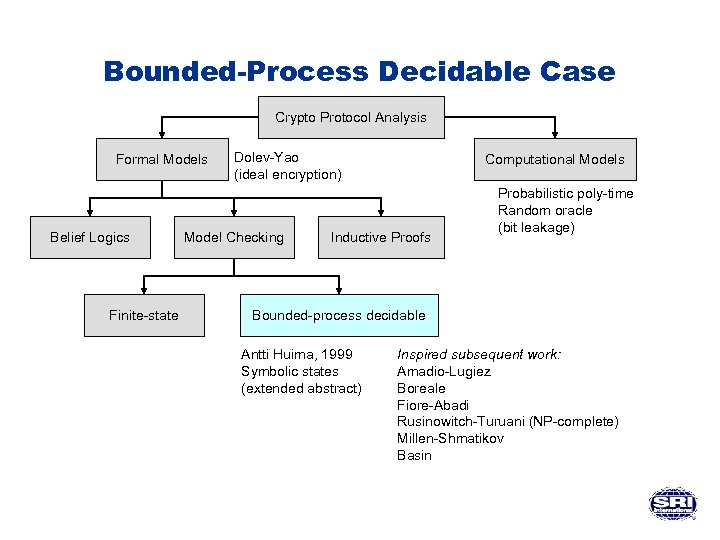
Bounded-Process Decidable Case Crypto Protocol Analysis Formal Models Belief Logics Finite-state Dolev-Yao (ideal encryption) Model Checking Computational Models Inductive Proofs Probabilistic poly-time Random oracle (bit leakage) Bounded-process decidable Antti Huima, 1999 Symbolic states (extended abstract) Inspired subsequent work: Amadio-Lugiez Boreale Fiore-Abadi Rusinowitch-Turuani (NP-complete) Millen-Shmatikov Basin

Constraint Solving l Millen-Shmatikov [MS 01] l Bounded-process decidable l Two-phase approach – Use the protocol spec to generate algebraic "constraint" sets – Use inference rules to solve constraint sets

Constraint Solving 1. Parametric strand specification for protocol 2. Choose N strand instances (small N) 3. Enumerate possible node orderings (strand interleavings) 4. Generate a constraint set for each ordering 5. Solve constraint set (finds attack) or prove unsolvable (N-secure) 6. No attack in any constraint set with N? Try N+1

Example Spec l NSPK protocol – "A"(A, B, Na, Nb) = + {A, Na}pk(B) – {Na, Nb}pk(A) + {Nb}pk(B) A B: {A, Na}pk(B) B A: {Na, Nb}pk(A) A B: {Nb}pk(B) – "B"(A, B, Na, Nb) = – {A, Na}pk(B) + {Na, Nb}pk(A) – {Nb}pk(B) Caution: variable scope is local to a strand. The "A" strand value of A is not necessarily equal to the "B" strand value of A (in a bundle).

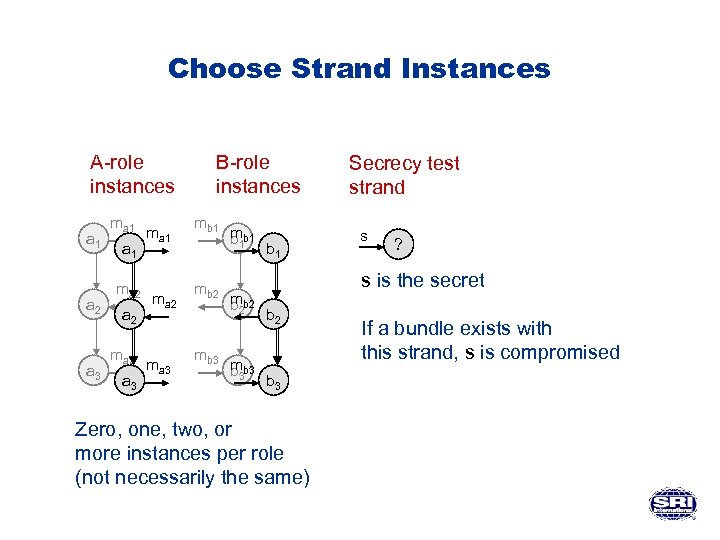
Choose Strand Instances A-role instances a 1 a 2 a 3 ma 1 ma 2 ma 3 B-role instances mb 1 mb 2 mb 3 b 1 Secrecy test strand s ? s is the secret b 2 b 3 Zero, one, two, or more instances per role (not necessarily the same) If a bundle exists with this strand, s is compromised

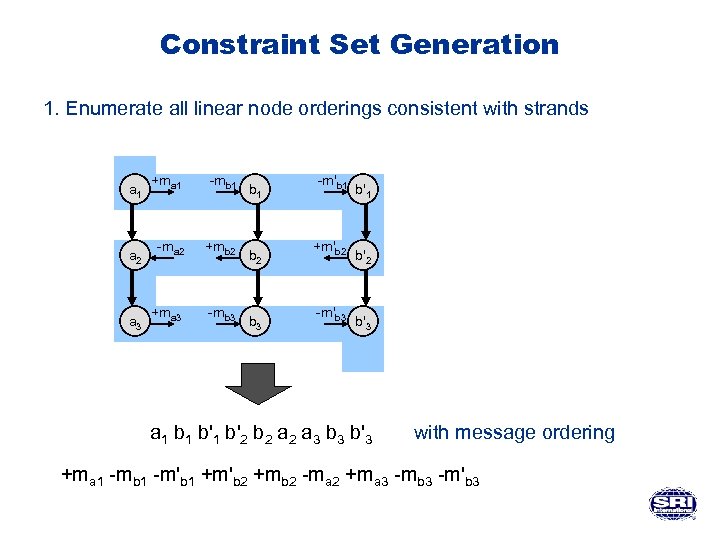
Constraint Set Generation 1. Enumerate all linear node orderings consistent with strands a 1 a 2 a 3 +ma 1 -mb 1 -ma 2 +mb 2 +ma 3 -mb 3 b 1 b 2 b 3 -m'b 1 +m'b 2 -m'b 3 b'1 b'2 b'3 a 1 b'1 b'2 b 2 a 3 b'3 with message ordering +ma 1 -mb 1 -m'b 1 +m'b 2 +mb 2 -ma 2 +ma 3 -mb 3 -m'b 3

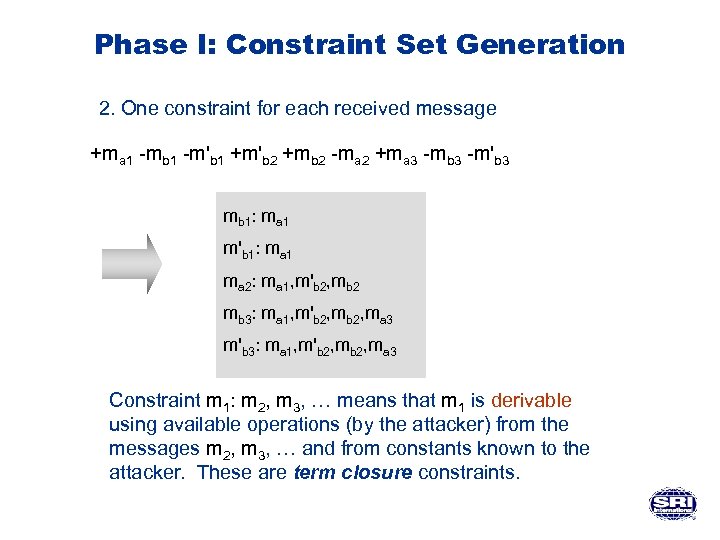
Phase I: Constraint Set Generation 2. One constraint for each received message +ma 1 -mb 1 -m'b 1 +m'b 2 +mb 2 -ma 2 +ma 3 -mb 3 -m'b 3 mb 1: ma 1 m'b 1: ma 1 ma 2: ma 1, m'b 2, mb 2 mb 3: ma 1, m'b 2, ma 3 m'b 3: ma 1, m'b 2, ma 3 Constraint m 1: m 2, m 3, … means that m 1 is derivable using available operations (by the attacker) from the messages m 2, m 3, … and from constants known to the attacker. These are term closure constraints.

Derivation Constraint Example A B: A original protocol "A"(A) = +A; "B"(A) = -A strand spec {+a, -A} semibundle +a -A interleaving A: a the constraint

How Many Interleavings? l For two strands of sizes m and n nodes, there are choose(m+n, n) different orderings (binomial coefficient) l Send optimization: +m 1, -m 2, … has at least as many solutions as -m 2, +m 1, … Therefore always choose send nodes first (order doesn't matter) l Common path optimization (Corin, Etalle) l Constraint differentiation (Basin, et al. ACM CCS '03)

Common Path Optimization l l l Node orderings have common initial subsequences Unsolvability of initial subsequence implies unsolvability of extensions Test solvability at every step to avoid fruitless extensions Implementation by Corin and Etalle, U. Twente, Holland Significant speed improvement A +a 1 B -b 1 -a 2 +b 2 +a 3 -b 3 -a 4 +a 1 -b 1 +b 2 -a 2 +a 3 -a 4 -b 3 Failure at a 2 eliminates second sequence

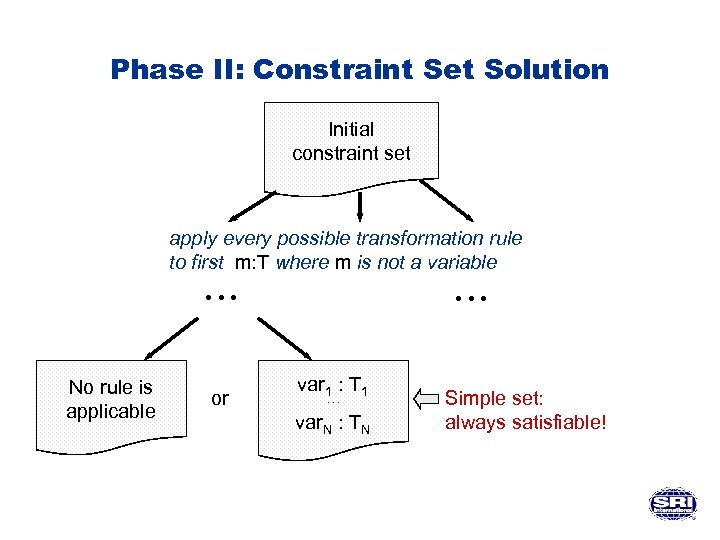
Phase II: Constraint Set Solution Initial constraint set apply every possible transformation rule to first m: T where m is not a variable • • • No rule is applicable or • • • var 1 : T 1 • • • var. N : TN Simple set: always satisfiable!

Some Transformation Rules Synthesis Analysis Other {x, y} : T ––––––– (pair) x: T y: T x : {y, z}, T –––– (split) x : y, z, T x : z, T –––––– (unify) unifies x, z partial solution {x}y : T –––––– (senc) x: T y: T x : {y}z, T ––––– (sdec) z : [{y}z], T x : y, z, T x : v, T –––––– (elim) x: T if v is a variable T is any set of terms [{y}z] is a marked encryption to prevent rule looping (elim) rule based on origination, monotonicity properties

Example CS Run in Prolog semibundle([Sa, Sb, St]) : strand(role. A, A, B, na, Nb, Sa), strand(role. B, A, B, Na, nb, Sb), strand(test, nb, St). ? - semibundle(B), search(B, []). Trace: recv([a, e]) send([a, na] * pk(e)) recv([a, na] * pk(b)) send([na, nb] * pk(a)) recv([na, nb] * pk(a)) send(nb * pk(e)) recv(nb * pk(b)) recv(nb)

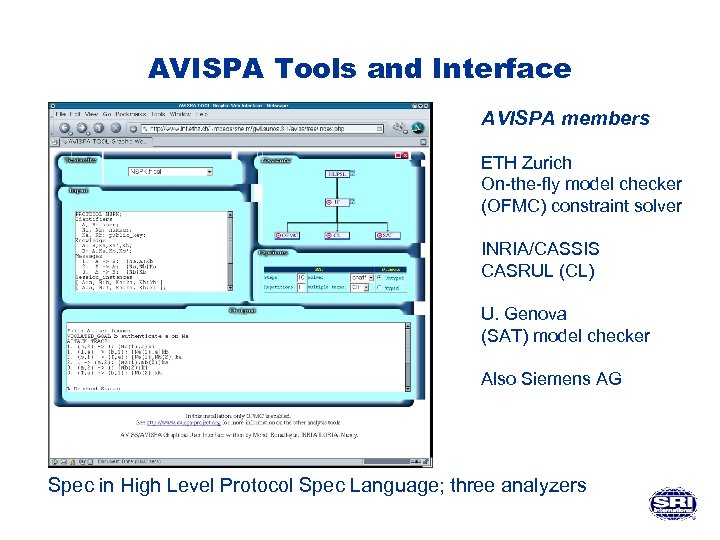
AVISPA Tools and Interface AVISPA members ETH Zurich On-the-fly model checker (OFMC) constraint solver INRIA/CASSIS CASRUL (CL) U. Genova (SAT) model checker Also Siemens AG Spec in High Level Protocol Spec Language; three analyzers

Some New Directions l Extension of decidable protocol analysis to (group) Diffie. Hellman and other associative-commutative operations – At SRI and independently at INRIA l Application of type theory to authentication protocol proofs – Type-safe implies attacker-unsafe; dependent types – Abadi-Blanchet, Debbabi-Mejri, Jeffrey l Derivation/composition of secure protocols – Datta-Derek-Mitchell-Pavlovic – Composition/transformation/refinement of functional components – Proof rules based on cord calculus (something like strand space) l Use of computationally ideal crypto primitives – Backes-Pfitzmann-Waidner (IBM Zurich) – Special crypto interface with implementation proved "ideal" – Can we use these operations for Dolev-Yao analysis?