Recent Advances in Parallel Implicit Solution of Fluid

Recent Advances in Parallel Implicit Solution of Fluid Plasma Systems (Wed. March 4 th, 2009) Part 1: MS 81 • 2: 00 -2: 25 Fully-Implicit Finite Element Formulations for Resistive Magneto. Hydrodynamic Systems – • • Kai Germaschewski, University of New Hampshire – Vyacheslav S. Lukin and Alan H. Glasser, University of Washington Dan Reynolds, Southern Methodist University; Ravi Samtaney, Princeton Plasma Physics Laboratory; Carol S. Woodward, Lawrence Livermore National Laboratory 5: 30 -5: 55 Progress in Parallel Implicit Methods for Tokamak Edge Plasma Modeling – • Ravi Samtaney, Princeton Plasma Physics Laboratory; Mark F. Adams, Columbia University; Achi Brandt, Weizmann Institute of Science, Israel 5: 00 -5: 25 A Preconditioned JFNK Method for Resistive MHD in a Mapped-grid. Tokamak Geometry – Luis Chacon, Oak Ridge National Laboratory 3: 30 -3: 55 Development and Applications of Hi. Fi -- Adaptive, Implicit, High Order Finite Element Code for General Multi-fluid Applications 4: 30 -4: 55 Nonlinear Multigrid. Methods for Fully Implicit Resistive MHD Simulations – 3: 00 -3: 25 The Magnetic Reconnection Code: Using Code Generation Techniques in an • Implicit Extended MHD Solver – • • 2: 30 -2: 55 Towards Full Braginskii. Implicit Extended MHD – • Roger Pawlowski and John Shadid, Sandia National Laboratories; Luis Chacon, Oak Ridge National Laboratory; Jeffrey Banks, Lawrence Livermore National Laboratory Part 2: MS 91 Lois Curfman Mc. Innes, Argonne National Laboratory; Sean Farley, Louisiana State University; Tom Rognlien and Maxim Umansky, Lawrence Livermore National Laboratory; Hong Zhang, Argonne National Laboratory 6: 00 -6: 25 Implicit Adaptive Mesh Refinement for 2 D Resistive Magnetohydrodynamics – Bobby Philip, Los Alamos National Laboratory; Luis Chacon, Oak Ridge National Laboratory; Michael Pernice, Idaho National Laboratory

Fully-Implicit Finite Element Formulations for Resistive Magneto-Hydrodynamic Systems R. P. Pawlowski, J. N. Shadid, and E. T. Phipps, Sandia National Laboratories L. Chacon, Los Alamos National Laboratory J. W. Banks, Lawrence Livermore National Laboratory SIAM Conference on Computational Science and Engineering Wednesday, March 4 th, 2009 Sandia is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the United States Department of Energy under Contract DE-AC 04 -94 AL 85000

Motivation Sandia Z-Machine Magnetohydrodynamics (MHD) describes a variety of important physics: Geophysics: Earth’s magnetosphere • Astrophysics: Solar Magnetosphere flares, These systems are characterized by a myriad of complex, interacting, sunspots, stars, Credit: Steele Hill/NASA interplanetary medium, nonlinear multiple time- and length-scale physical mechanisms. nebulae etc. . . • Fusion: Tokamak, Stellerator • Engineering: plasma confinement, liquid metal transfer, nuclear reactors, etc. . . • Inertial confinement fusion (Rayleigh-Taylor instabilities) NIMROD • ITER FSP Report

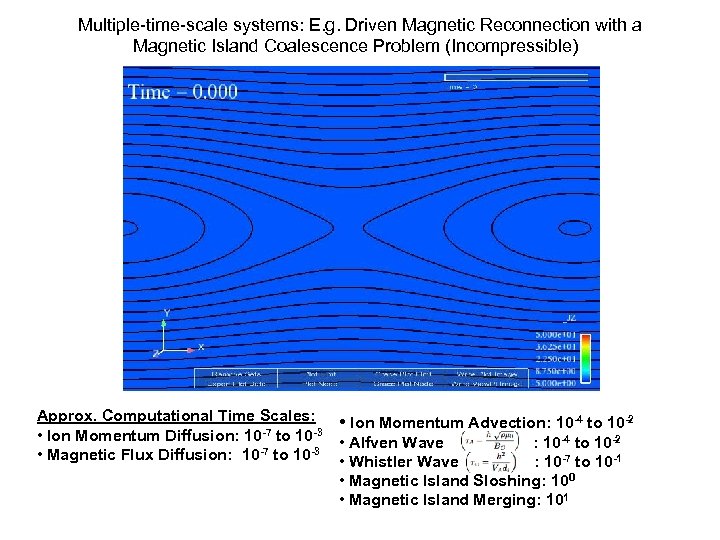Multiple-time-scale systems: E. g. Driven Magnetic Reconnection with a Magnetic Island Coalescence Problem (Incompressible) Approx. Computational Time Scales: • Ion Momentum Diffusion: 10 -7 to 10 -3 • Magnetic Flux Diffusion: 10 -7 to 10 -3 • Ion Momentum Advection: 10 -4 to 10 -2 • Alfven Wave : 10 -4 to 10 -2 • Whistler Wave : 10 -7 to 10 -1 • Magnetic Island Sloshing: 100 • Magnetic Island Merging: 101

The Goal: Stable, Accurate, Scalable, and Efficient x. MHD Unstructured FE Solution Methods • Why fully Implicit? – Stability (stiff systems) – Accuracy (high order, variable order, local and global error control, . . . ) – Use time steps on the size of the dynamics of interest (no CFL constraint) – Avoid instabilities from operator splitting ( Ropp and Shadid, JCP 2005) – Allows direct stability and bifurcation analysis (Salinger al. IJBC 2005) et – Allows embedded (fast) optimization (Bartlett al. SAND 2003) et • Develop scalable solvers: physics-based/multi-level preconditioners • Develop stabilized and compatible x. MHD formulations using unstructured FE • Produce large-scale computational demonstrations of MHD Systems • Magnetic Reconnection Studies • Hydro-Magnetic Rayleigh-Taylor (e. g. Z-pinch [HEDP]) • Hydromagnetic. Rayleigh-Bernard (towards geo-dynamo effects) • Fusion Energy ( Tokamak etc…)

Resistive, Extended MHD Equations Extended MHD Model in Residual Form Involution: Divergence Conservation Form Involution: General Case a Strongly Coupled, Multiple Time- and Length-Scale, Nonlinear, Nonsymmetric System with Parabolic and Hyperbolic Character

Formulations • Multiple formulations are used to enforce the solenoidal involution: , and to address conservation. 1. 2. 3. 4. Vector Potential (2 D) Projection (3 D) Lagrange Multiplier w/ VMS (3 D) Compatible discretizations (mixed Node/Edge/Face Elements)

Magnetic Vector Potential Formulation (2 D) Solenoidal involution is automatically satisfied provided that the discrete differential operator enforces to machine accuracy. Select a Gauge and in 2 D • For 2 D Linear Lagrange Elements: Divergence free condition is satisfied to machine precision point-wise on element interiors and in an L 2 sense over any sub-region of the domain (but not necessarily on the element boundaries since C 0 elements are used). • Convection/Diffusion/Reaction equation can use SUPG Stabilization.

Summary of Initial Stabilized FE Weak form of Equations for Low Mach Number MHD System Governing Equation Momentum Total Mass Thermal Energy Magnetics (Vector Potential) Stabilized FE Residual (following Hughes et. al. , Shakib - Navier-Stokes; extension of Codina et. al. -Magnetics)

3 D Lagrange Multiplier Formulation (Munz 2000, Dedner 2002, Codina 2006) Remarks: • Elliptic constraint used to enforce divergence free condition. • Only weakly divergence free in FE implementation • VMS formulation for convection & coupling effects under development

Stabilization to circumvent inf-sup (LBB) condition(s): Consistent, residual based stabilization (Hughes et al. ): Regularization (Dohrman-Bochev-Gunzburger): Similar algorithms used for Magnetics equation and solenoidal constraint:

• Low Mach Number Resistive MHD • Initial MHD Formulations: trilinos. sandia. gov – 2 D Vector Potential – 2 D & 3 D B field Projection – Lagrange Multiplier Method (VMS) Nonlinear equations: • Massively Parallel: MPI • 2 D & 3 D Unstructured Stabilized FE • Fully Coupled Globalized Newton-Krylov solver Newton System: – Sensitivities: Templated C++, Automatic Differentiation (Saccado) – GMRES (Aztec. OO, Belos) – Additive Schwarz DD w/ Var. Overlap (Ifpack, Aztec. OO) – Aggressive Coarsening Graph Based Block Multilevel [AMG] for Systems (ML) • Fully-implicit: 1 st-5 th variable order BDF (Rythmos) & native integrator • Direct-to-Steady-State (NOX), Continuation, Linear Stability and Bifurcation (LOCA / Anasazi), PDE Constrained Optimization (Moocho) Sensitivities:

Results and Analysis • Formulation Verification (selected examples) – Flux Expulsion (Unstructured Mesh) – Alfven Wave (spatial and temporal order of accuracy) • Scalability and Multicore • Stability and Bifurcation Analysis • Magnetic Reconnection

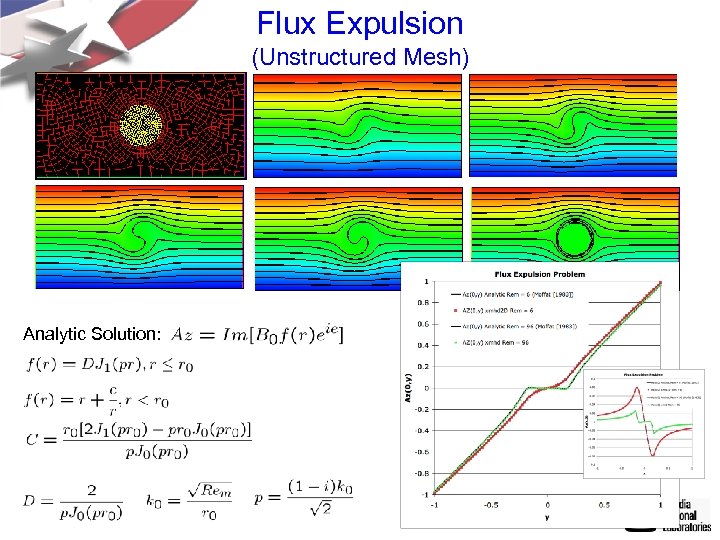Flux Expulsion (Unstructured Mesh) Analytic Solution:

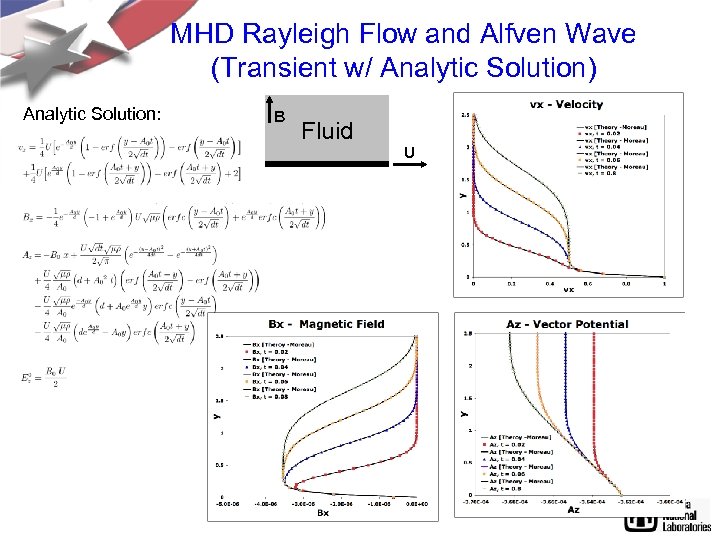MHD Rayleigh Flow and Alfven Wave (Transient w/ Analytic Solution) Analytic Solution: B Fluid U

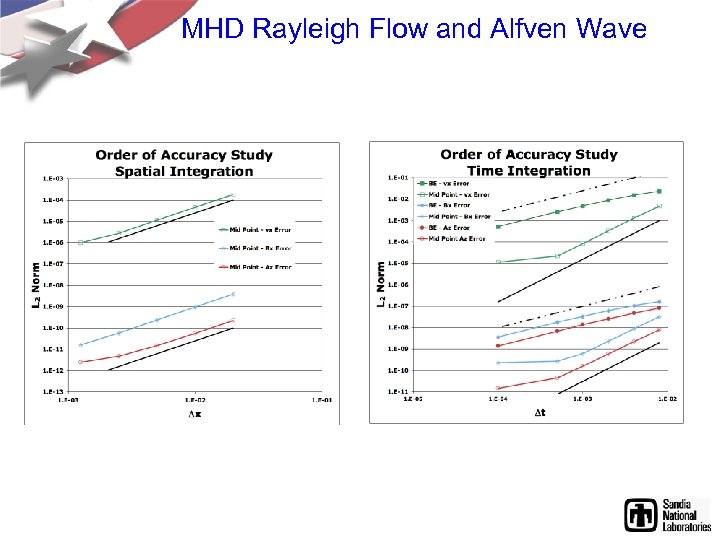MHD Rayleigh Flow and Alfven Wave

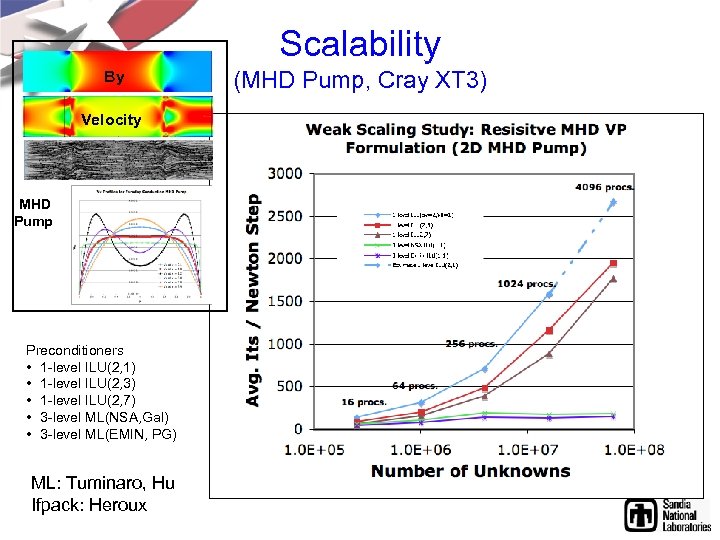Scalability By Velocity MHD Pump Preconditioners • 1 -level ILU(2, 1) • 1 -level ILU(2, 3) • 1 -level ILU(2, 7) • 3 -level ML(NSA, Gal) • 3 -level ML(EMIN, PG) ML: Tuminaro, Hu Ifpack: Heroux (MHD Pump, Cray XT 3)

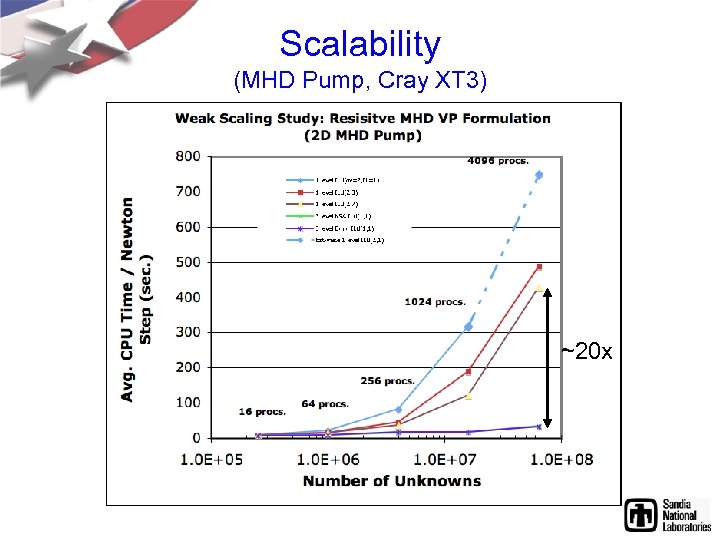Scalability (MHD Pump, Cray XT 3) ~20 x

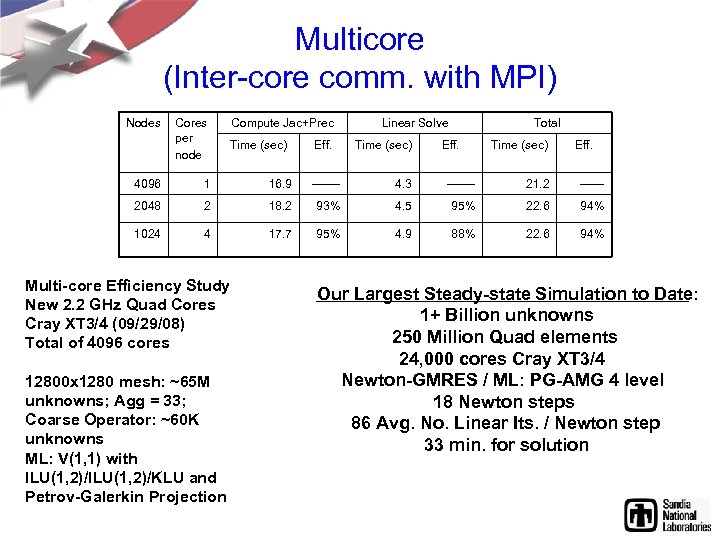Multicore (Inter-core comm. with MPI) Nodes Cores per node Compute Jac+Prec Time (sec) Eff. Linear Solve Time (sec) Total Eff. Time (sec) Eff. 4096 1 16. 9 ------- 4. 3 ------- 21. 2 ------ 2048 2 18. 2 93% 4. 5 95% 22. 6 94% 1024 4 17. 7 95% 4. 9 88% 22. 6 94% Multi-core Efficiency Study New 2. 2 GHz Quad Cores Cray XT 3/4 (09/29/08) Total of 4096 cores 12800 x 1280 mesh: ~65 M unknowns; Agg = 33; Coarse Operator: ~60 K unknowns ML: V(1, 1) with ILU(1, 2)/KLU and Petrov-Galerkin Projection Our Largest Steady-state Simulation to Date: 1+ Billion unknowns 250 Million Quad elements 24, 000 cores Cray XT 3/4 Newton-GMRES / ML: PG-AMG 4 level 18 Newton steps 86 Avg. No. Linear Its. / Newton step 33 min. for solution

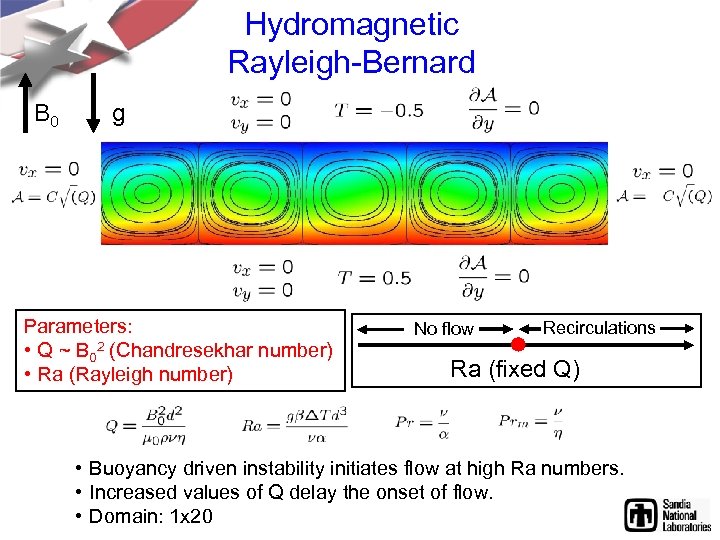Hydromagnetic Rayleigh-Bernard B 0 g Parameters: • Q ~ B 02 (Chandresekhar number) • Ra (Rayleigh number) No flow Recirculations Ra (fixed Q) • Buoyancy driven instability initiates flow at high Ra numbers. • Increased values of Q delay the onset of flow. • Domain: 1 x 20

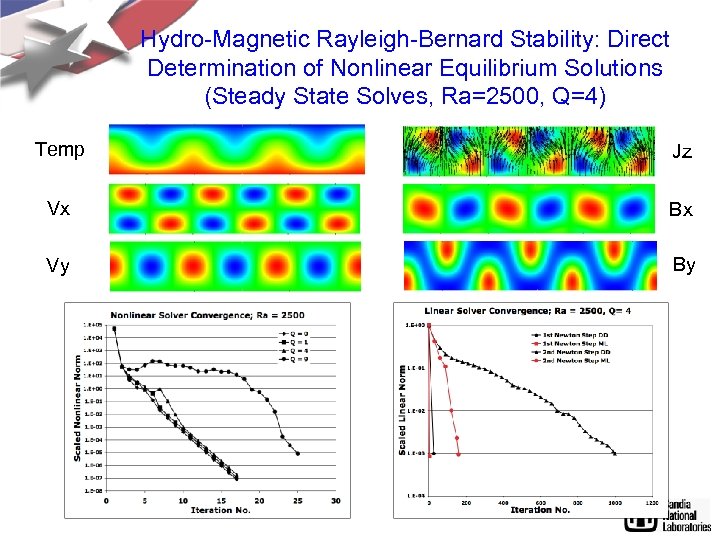Hydro-Magnetic Rayleigh-Bernard Stability: Direct Determination of Nonlinear Equilibrium Solutions (Steady State Solves, Ra=2500, Q=4) Temp Jz Vx Bx Vy By

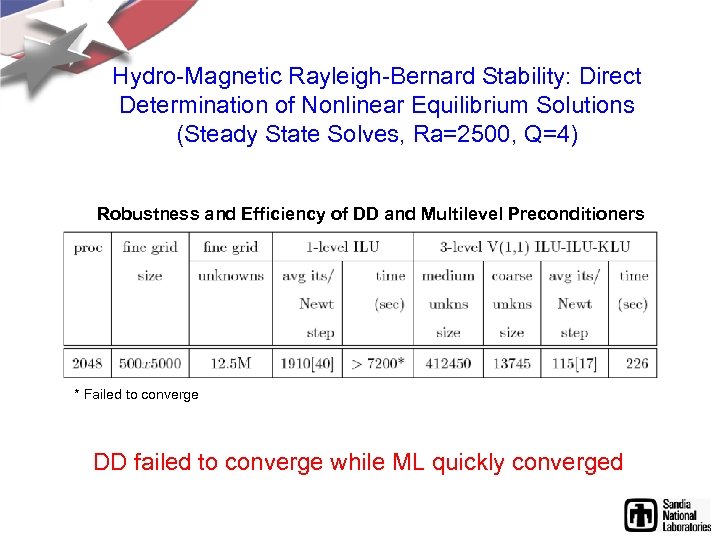Hydro-Magnetic Rayleigh-Bernard Stability: Direct Determination of Nonlinear Equilibrium Solutions (Steady State Solves, Ra=2500, Q=4) Robustness and Efficiency of DD and Multilevel Preconditioners * Failed to converge DD failed to converge while ML quickly converged

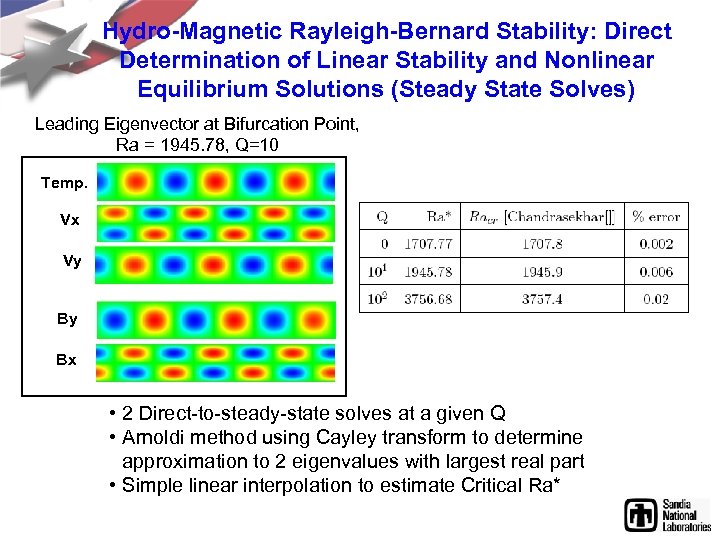Hydro-Magnetic Rayleigh-Bernard Stability: Direct Determination of Linear Stability and Nonlinear Equilibrium Solutions (Steady State Solves) Leading Eigenvector at Bifurcation Point, Ra = 1945. 78, Q=10 Temp. Vx Vy By Bx • 2 Direct-to-steady-state solves at a given Q • Arnoldi method using Cayley transform to determine approximation to 2 eigenvalues with largest real part • Simple linear interpolation to estimate Critical Ra*

HRB Shutdown Ra = 4000 Vx, B • Q=81: Flow recirculations present! • Q=144: Zero flow solution! Jz, B

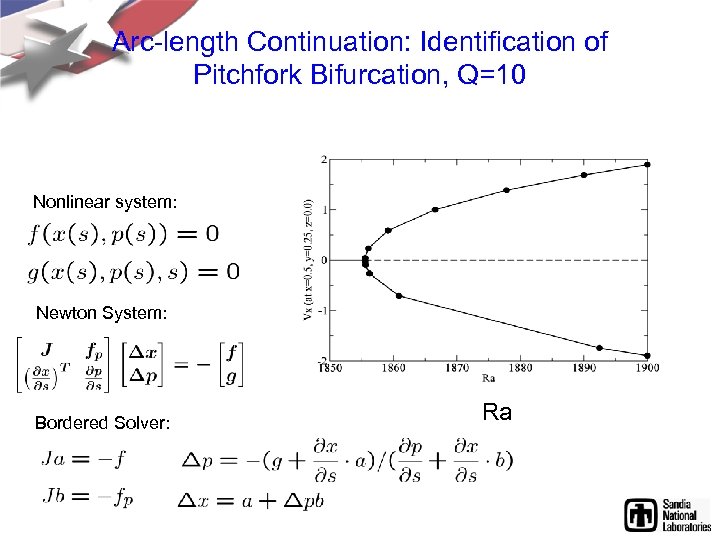Arc-length Continuation: Identification of Pitchfork Bifurcation, Q=10 Nonlinear system: Newton System: Bordered Solver: Ra

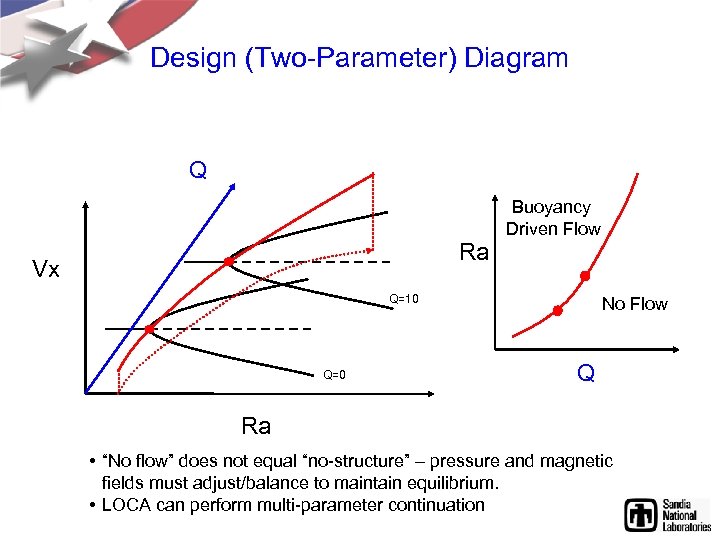Design (Two-Parameter) Diagram Q Ra Vx Buoyancy Driven Flow Q=10 Q=0 No Flow Q Ra • “No flow” does not equal “no-structure” – pressure and magnetic fields must adjust/balance to maintain equilibrium. • LOCA can perform multi-parameter continuation

Bifurcation Tracking Moore-Spence (Govaerts 2000) Minimally Augmented • Turning point formulation: • Widely used algorithm for small systems: • Newton’s method (2 N+1): • J is singular if and only if s = 0 • Turning point formulation (N+1): • 4 linear solves per Newton iteration: • Newton’s method: • 3 linear solves per Newton iteration Extension to large-scale iterative solvers

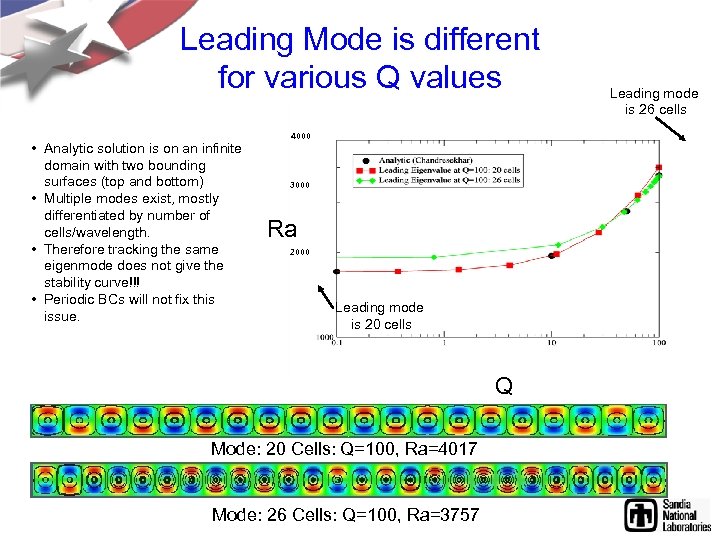Leading Mode is different for various Q values • Analytic solution is on an infinite domain with two bounding surfaces (top and bottom) • Multiple modes exist, mostly differentiated by number of cells/wavelength. • Therefore tracking the same eigenmode does not give the stability curve!!! • Periodic BCs will not fix this issue. 4000 3000 Ra 2000 Leading mode is 20 cells Q Mode: 20 Cells: Q=100, Ra=4017 Mode: 26 Cells: Q=100, Ra=3757 Leading mode is 26 cells

Impact of Numerical Algorithms on Scientific Discovery • Much work has been done to understand the Island Coalescence problem [1 -9]. • GOAL: Understand limits in driven magnetic reconnection • Poor numerical tools (dissipative, inefficient) led scientists to “find” an asymptotic regime with h independent reconnection rates (fast) [2, 3, 4]. • Novel JFNK algorithms with strict control of dissipation set the record straight • There is no true fast reconnection asymptotic region [8, 9]. 1. 2. 3. 4. 5. 6. 7. 8. 9. J. M. Finn and P. K. Kaw, Phys. Fluids 20, 72, 1977 P. L. Pritchett and C. C. Wu, Phys. Fluids 22, 2140, 1979 D. Biskamp and H. Welter, Phys. Rev. Letters 44, 1069, 1980 D. Biskamp, Phys. Rev. Lett 87 A, 357, 1982 A. Battacharjee, F. Brunel, and T. Tajima, Phys. Fluids 26, 3332, 1983 G. J. Rickard and I. J. D. Craig, Phys. Fluids B 5, 956, 1993 J. C. Dorelli, and J. Birn, J. Geophys. Res. 108, 1133, 2003 D. Knoll and L. Chacon, Phys. Plasmas, 13 (3), 032307, 2006 D. Knoll and L. Chacon, Phys. Rev. Letters. , 96, 135001, 2006

Unstructured Mesh and Solution t=0. 0 t=9. 0 t=10. 0 t=12. 0

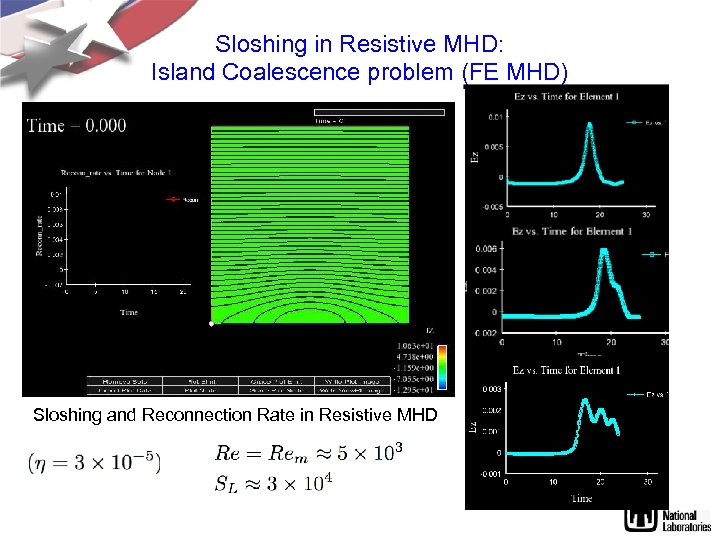Sloshing in Resistive MHD: Island Coalescence problem (FE MHD) Sloshing and Reconnection Rate in Resistive MHD

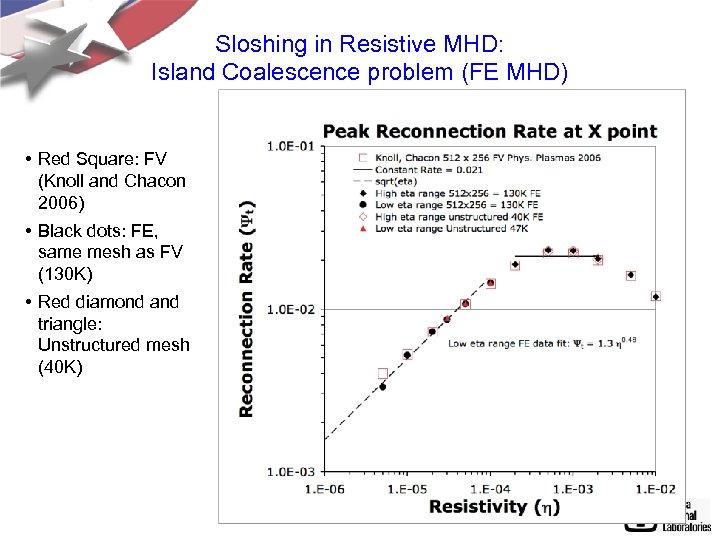Sloshing in Resistive MHD: Island Coalescence problem (FE MHD) • Red Square: FV (Knoll and Chacon 2006) • Black dots: FE, same mesh as FV (130 K) • Red diamond and triangle: Unstructured mesh (40 K)

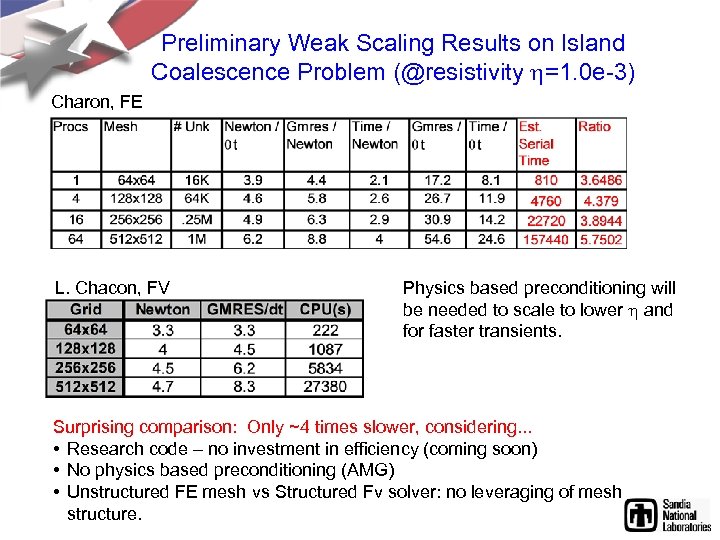Preliminary Weak Scaling Results on Island Coalescence Problem (@resistivity h=1. 0 e-3) Charon, FE L. Chacon, FV Physics based preconditioning will be needed to scale to lower h and for faster transients. Surprising comparison: Only ~4 times slower, considering. . . • Research code – no investment in efficiency (coming soon) • No physics based preconditioning (AMG) • Unstructured FE mesh vs Structured Fv solver: no leveraging of mesh structure.

Summary • New unstructured grid, fully implicit, Stabilized FEM developed for single-fluid resistive MHD equations. • Demonstrating important capabilities: – Fundamental discretization algorithms (unstructured implicit FE) – Analysis Tools: Stability/Bifurcation Tracking • Able to reproduce difficult magnetic reconnection results. • Largest problem to date: 1 Billion unknowns on 24, 000 cores (Cray XT 3/4).